skimage.metrics#
根据SNEMI3D竞赛定义计算调整后的Rand误差。 |
|
返回匹配分割中所有区域的列联表。 |
|
计算给定图像中非零元素之间的豪斯多夫距离。 |
|
返回给定图像中非零元素之间的Hausdorff距离的一对点。 |
|
计算两幅图像之间的均方误差。 |
|
计算归一化互信息(NMI)。 |
|
计算两幅图像之间的归一化均方根误差(NRMSE)。 |
|
计算图像的峰值信噪比(PSNR)。 |
|
计算两幅图像之间的平均结构相似性指数。 |
|
返回与 VI 相关的对称条件熵。 |
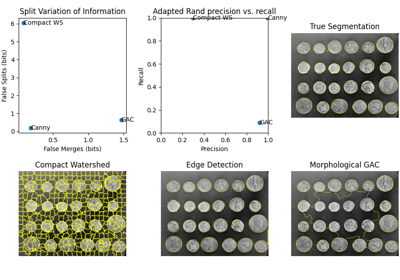
- skimage.metrics.adapted_rand_error(image_true=None, image_test=None, *, table=None, ignore_labels=(0,), alpha=0.5)[源代码][源代码]#
计算根据SNEMI3D竞赛定义的适应兰德误差。 [1]
- 参数:
- image_trueint 的 ndarray
地面实况标签图像,与 im_test 形状相同。
- image_testint 的 ndarray
测试图像。
- 表scipy.sparse 的 crs 格式数组,可选
使用 skimage.evaluate.contingency_table 构建的列联表。如果为 None,它将在运行时计算。
- 忽略标签int 序列,可选
忽略的标签。真实图像中任何带有这些值的部分都不会计入分数。
- alphafloat, 可选
在调整兰德误差计算中,给予精确度和召回率的相对权重。
- 返回:
- 是浮动
适应的 Rand 误差。
- prec浮动
适应的 Rand 精度:这是在测试标签图像 和 真实图像中具有相同标签的像素对数,除以测试图像中的像素对数。
- rec浮动
调整后的 Rand 召回率:这是在测试标签图像 和 真实图像中具有相同标签的像素对数,除以真实图像中的像素对数。
注释
在真实分割中标签为0的像素在评分中被忽略。
适应的 Rand 误差计算如下:
\(1 - \frac{\sum_{ij} p_{ij}^{2}}{\alpha \sum_{k} s_{k}^{2} + (1-\alpha)\sum_{k} t_{k}^{2}}\), 其中 \(p_{ij}\) 是像素在测试图像和真实图像中具有相同标签的概率,\(t_{k}\) 是像素在真实图像中具有标签 \(k\) 的概率,而 \(s_{k}\) 是像素在测试图像中具有标签 \(k\) 的概率。
默认行为是在适应的Rand误差计算中同等加权精确度和召回率。当alpha = 0时,适应的Rand误差 = 召回率。当alpha = 1时,适应的Rand误差 = 精确度。
参考文献
[1]Arganda-Carreras I, Turaga SC, Berger DR, 等. (2015) 众包创建连接组学图像分割算法。Front. Neuroanat. 9:142. DOI:10.3389/fnana.2015.00142
- skimage.metrics.contingency_table(im_true, im_test, *, ignore_labels=None, normalize=False)[源代码][源代码]#
返回匹配分割中所有区域的列联表。
- 参数:
- im_trueint 的 ndarray
地面实况标签图像,与 im_test 形状相同。
- im_testint 的 ndarray
测试图像。
- 忽略标签int 序列,可选
忽略的标签。真实图像中任何带有这些值的部分都不会计入分数。
- 规范化布尔
确定是否通过像素计数对列联表进行归一化。
- 返回:
- contscipy.sparse.csr_matrix
一个列联表。cont[i, j] 将等于在 im_true 中标记为 i 并且在 im_test 中标记为 j 的体素数量。
- skimage.metrics.hausdorff_distance(image0, image1, method='standard')[源代码][源代码]#
计算给定图像中非零元素之间的豪斯多夫距离。
- 参数:
- image0, image1ndarray
数组中
True表示该点包含在一组点中。两个数组必须具有相同的形状。- 方法{‘standard’, ‘modified’}, 可选, 默认 = ‘standard’
计算Hausdorff距离的方法。
standard是标准的Hausdorff距离,而modified是改进的Hausdorff距离。
- 返回:
- 距离浮动
image0和image1中非零像素坐标之间的 Hausdorff 距离,使用欧几里得距离。
注释
Hausdorff 距离 [1] 是
image0上任意一点到image1上最近点的最大距离,反之亦然。Dubuisson 等人的研究 [2] 表明,改进的 Hausdorff 距离 (MHD) 在性能上优于有向 Hausdorff 距离 (HD)。该函数计算前向和后向的平均距离,并返回两者中较大的一个。参考文献
[2]M. P. Dubuisson and A. K. Jain. A Modified Hausdorff distance for object matching. In ICPR94, pages A:566-568, Jerusalem, Israel, 1994. DOI:10.1109/ICPR.1994.576361 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.1.8155
示例
>>> points_a = (3, 0) >>> points_b = (6, 0) >>> shape = (7, 1) >>> image_a = np.zeros(shape, dtype=bool) >>> image_b = np.zeros(shape, dtype=bool) >>> image_a[points_a] = True >>> image_b[points_b] = True >>> hausdorff_distance(image_a, image_b) 3.0
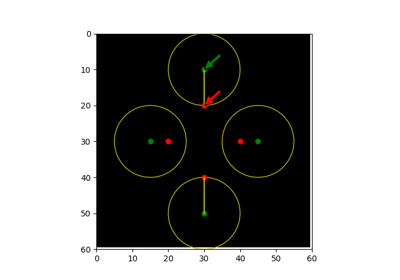
- skimage.metrics.hausdorff_pair(image0, image1)[源代码][源代码]#
返回给定图像中非零元素之间的Hausdorff距离的一对点。
Hausdorff 距离 [1] 是
image0上任意一点到image1上最近点的最大距离,反之亦然。- 参数:
- image0, image1ndarray
数组中
True表示该点包含在一组点中。两个数组必须具有相同的形状。
- 返回:
- 点_a, 点_b数组
一对点,它们之间的Hausdorff距离。
参考文献
示例
>>> points_a = (3, 0) >>> points_b = (6, 0) >>> shape = (7, 1) >>> image_a = np.zeros(shape, dtype=bool) >>> image_b = np.zeros(shape, dtype=bool) >>> image_a[points_a] = True >>> image_b[points_b] = True >>> hausdorff_pair(image_a, image_b) (array([3, 0]), array([6, 0]))
- skimage.metrics.mean_squared_error(image0, image1)[源代码][源代码]#
计算两幅图像之间的均方误差。
- 参数:
- image0, image1ndarray
图像。任何维度,必须具有相同的形状。
- 返回:
- mse浮动
均方误差 (MSE) 指标。
注释
在 0.16 版本发生变更: 此函数已从
skimage.measure.compare_mse重命名为skimage.metrics.mean_squared_error。
- skimage.metrics.normalized_mutual_information(image0, image1, *, bins=100)[源代码][源代码]#
计算归一化互信息(NMI)。
\(A\) 和 \(B\) 的归一化互信息由以下公式给出:
.. math::
Y(A, B) = frac{H(A) + H(B)}{H(A, B)}
其中 \(H(X) := - \sum_{x \in X}{x \log x}\) 是熵。
Colin Studholme 及其同事 [1] 提出,它在注册图像时非常有用。其范围从 1(图像值完全不相关)到 2(图像值完全相关,无论是正相关还是负相关)。
- 参数:
- image0, image1ndarray
待比较的图像。两个输入图像必须具有相同数量的维度。
- binsint 或 int 序列,可选
联合直方图每个轴上的箱数。
- 返回:
- nmi浮动
这两个数组之间的归一化互信息,在由
bins给定的粒度上计算。NMI 越高,输入图像越相似。
- Raises:
- ValueError
如果图像的维度数量不同。
注释
如果两个输入图像的形状不同,较小的图像会用零填充。
参考文献
[1]C. Studholme, D.L.G. Hill, & D.J. Hawkes (1999). An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition 32(1):71-86 DOI:10.1016/S0031-3203(98)00091-0
- skimage.metrics.normalized_root_mse(image_true, image_test, *, normalization='euclidean')[源代码][源代码]#
计算两幅图像之间的归一化均方根误差(NRMSE)。
- 参数:
- image_truendarray
地面实况图像,与 im_test 形状相同。
- image_testndarray
测试图像。
- 规范化{‘欧几里得’, ‘最小-最大’, ‘平均’}, 可选
控制用于NRMSE分母中的归一化方法。文献中没有标准的归一化方法 [1]。这里可用的方法如下:
‘euclidean’ : 通过
im_true的平均欧几里得范数进行归一化:NRMSE = RMSE * sqrt(N) / || im_true ||
其中 || . || 表示 Frobenius 范数,
N = im_true.size。这个结果等价于:NRMSE = || im_true - im_test || / || im_true ||.
‘min-max’ : 通过
im_true的强度范围进行归一化。‘mean’ : 通过
im_true的平均值进行归一化
- 返回:
- nrmse浮动
NRMSE 指标。
注释
在 0.16 版本发生变更: 此函数已从
skimage.measure.compare_nrmse重命名为skimage.metrics.normalized_root_mse。参考文献
[1]
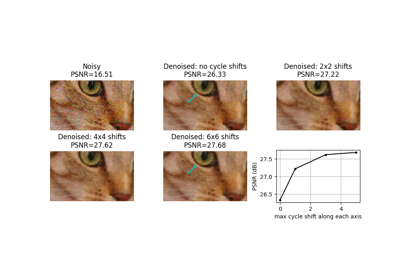
- skimage.metrics.peak_signal_noise_ratio(image_true, image_test, *, data_range=None)[源代码][源代码]#
计算图像的峰值信噪比(PSNR)。
- 参数:
- image_truendarray
地面实况图像,与 im_test 形状相同。
- image_testndarray
测试图像。
- 数据范围int, 可选
输入图像的数据范围(最小值和最大值之间的距离)。默认情况下,这是根据图像数据类型估计的。
- 返回:
- psnr浮动
PSNR 指标。
注释
在 0.16 版本发生变更: 此函数已从
skimage.measure.compare_psnr重命名为skimage.metrics.peak_signal_noise_ratio。参考文献
[1]
- skimage.metrics.structural_similarity(im1, im2, *, win_size=None, gradient=False, data_range=None, channel_axis=None, gaussian_weights=False, full=False, **kwargs)[源代码][源代码]#
计算两幅图像之间的平均结构相似性指数。请注意浮点图像的 data_range 参数。
- 参数:
- im1, im2ndarray
图像。任何维度,形状相同。
- win_sizeint 或 None, 可选
用于比较的滑动窗口的边长。必须是奇数值。如果 gaussian_weights 为 True,则忽略此值,窗口大小将取决于 sigma。
- 梯度bool, 可选
如果为 True,则同时返回相对于 im2 的梯度。
- 数据范围float, 可选
输入图像的数据范围(最大可能值与最小可能值之间的差异)。默认情况下,这是根据图像数据类型估算的。对于浮点图像数据,此估算可能不正确。因此,建议始终显式传递此标量值(见下文注释)。
- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19:
channel_axis在 0.19 版本中被添加。- gaussian_weightsbool, 可选
如果为真,每个补丁的均值和方差将根据宽度为 sigma=1.5 的归一化高斯核进行空间加权。
- 完整bool, 可选
如果为真,还返回完整的结构相似性图像。
- 返回:
- mssim浮动
图像的平均结构相似性指数。
- 梯度ndarray
im1 和 im2 之间的结构相似性梯度 [2]。只有在 gradient 设置为 True 时才会返回。
- Sndarray
完整的 SSIM 图像。仅当 full 设置为 True 时返回。
- 其他参数:
注释
如果未指定 data_range,则根据图像数据类型自动猜测范围。然而,对于浮点图像数据,此估计值会得到所需范围的两倍,因为 skimage.util.dtype.py 中的 dtype_range 定义了从 -1 到 +1 的区间。这会产生一个估计值 2,而不是通常在处理图像数据时所需的 1(因为负光强度是无意义的)。在处理类似 YCbCr 的颜色数据时,请注意这些范围在每个通道上有所不同(Cb 和 Cr 的范围是 Y 的两倍),因此不能通过一次调用此函数来计算通道平均的 SSIM,因为假定每个通道的范围相同。
要匹配 Wang 等人 [1] 的实现,请将 gaussian_weights 设置为 True,sigma 设置为 1.5,use_sample_covariance 设置为 False,并指定 data_range 参数。
在 0.16 版本发生变更: 此函数已从
skimage.measure.compare_ssim重命名为skimage.metrics.structural_similarity。参考文献
[1] (1,2,3)Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). 图像质量评估:从误差可见性到结构相似性。IEEE 图像处理汇刊, 13, 600-612. https://ece.uwaterloo.ca/~z70wang/publications/ssim.pdf, DOI:10.1109/TIP.2003.819861
[2]Avanaki, A. N. (2009). 精确全局直方图规范优化用于结构相似性。光学评论, 16, 613-621. arXiv:0901.0065 DOI:10.1007/s10043-009-0119-z
- skimage.metrics.variation_of_information(image0=None, image1=None, *, table=None, ignore_labels=())[源代码][源代码]#
返回与 VI 相关的对称条件熵。 [1]
信息的变异定义为 VI(X,Y) = H(X|Y) + H(Y|X)。如果 X 是真实分割,那么 H(X|Y) 可以解释为欠分割的量,H(Y|X) 为过分割的量。换句话说,一个完美的过分割将有 H(X|Y)=0,而一个完美的欠分割将有 H(Y|X)=0。
- 参数:
- image0, image1int 的 ndarray
标注图像/分割,必须具有相同的形状。
- 表scipy.sparse 的 csr 格式数组,可选
使用 skimage.evaluate.contingency_table 构建的列联表。如果为 None,将使用 skimage.evaluate.contingency_table 计算。如果给出,熵将从该表中计算,任何图像将被忽略。
- 忽略标签int 序列,可选
忽略的标签。真实图像中任何带有这些值的部分都不会计入分数。
- 返回:
- vi浮点数 ndarray,形状 (2,)
图像1|图像0 和 图像0|图像1 的条件熵。
参考文献
[1]Marina Meilă (2007), 比较聚类—基于信息论的距离, 多元分析杂志, 第98卷, 第5期, 第873-895页, ISSN 0047-259X, DOI:10.1016/j.jmva.2006.11.013.