skimage.util#
通用实用函数。
此模块包含一些通用的图像处理实用函数。
在数组上并行映射一个函数。 |
|
返回一张显示两张图片之间差异的图片。 |
|
沿每个维度裁剪数组 ar 的 crop_width。 |
|
返回图像数据类型的强度限制,即 (最小值, 最大值) 元组。 |
|
将图像转换为布尔格式。 |
|
将图像转换为浮点格式。 |
|
将图像转换为单精度(32位)浮点格式。 |
|
将图像转换为双精度(64位)浮点格式。 |
|
将图像转换为16位有符号整数格式。 |
|
将图像转换为8位无符号整数格式。 |
|
将图像转换为16位无符号整数格式。 |
|
反转图像。 |
|
为图像掩码上的坐标分配唯一的整数标签 |
|
在 scikit-image 文档字符串中进行关键词搜索并打印结果。 |
|
将输入数组 input_vals 中的值映射到 output_vals。 |
|
创建一个由多个单通道或多通道图像组成的蒙太奇。 |
|
向浮点图像添加各种类型随机噪声的函数。 |
|
在 ar_shape 上找到 n_points 个等间距的点。 |
|
返回一张包含 ~`n_points` 个等间距非零像素的图像。 |
|
沿给定轴切割图像。 |
|
从二维数组中移除重复的行。 |
|
输入 n 维数组的块视图(使用重新分块)。 |
|
输入 n 维数组的滚动窗口视图。 |
- skimage.util.apply_parallel(function, array, chunks=None, depth=0, mode=None, extra_arguments=(), extra_keywords=None, *, dtype=None, compute=None, channel_axis=None)[源代码][源代码]#
在数组上并行映射一个函数。
将一个数组分割成可能重叠的块,块的深度和边界类型由给定参数决定,在块上并行调用给定的函数,合并块并返回结果数组。
- 参数:
- 函数函数
要映射的函数,该函数接受一个数组作为参数。
- 数组numpy 数组或 dask 数组
函数将应用到的数组。
- 块int, tuple, 或 tuple 的 tuple, 可选
单个整数被解释为正方形块的一边的长度,该正方形块应在数组上平铺。长度为
array.ndim的元组表示块的形状,并在数组上平铺。长度为ndim的元组列表,其中每个子元组是沿相应维度的块大小序列。如果为 None,则根据可用 CPU 的数量将数组分解为块。有关块的更多信息,请参阅文档 这里。当 channel_axis 不为 None 时,元组的长度可以是ndim - 1,并且将在通道轴上使用单个块。- 深度int 或 int 序列,可选
添加的边界单元格的深度。可以使用元组为每个数组轴指定不同的深度。默认为零。当 channel_axis 不为 None,并且提供了一个长度为
ndim - 1的元组时,通道轴将使用深度 0。- 模式{‘reflect’, ‘symmetric’, ‘periodic’, ‘wrap’, ‘nearest’, ‘edge’}, 可选
外部边界填充的类型。
- extra_argumentstuple, 可选
传递给函数的参数元组。
- extra_keywords字典,可选
要传递给函数的关键字参数字典。
- dtype数据类型 或 None, 可选
function 输出的数据类型。如果为 None,Dask 将尝试通过在形状为
(1,) * ndim的数据上调用函数来推断此类型。对于期望 RGB 或多通道数据的函数,这可能会出现问题。在这种情况下,用户应手动指定此 dtype 参数。Added in version 0.18:
dtype在 0.18 版本中被添加。- 计算bool, 可选
如果
True,则立即计算并返回一个 NumPy 数组。如果False,则延迟计算并返回一个 Dask 数组。如果 ``None``(默认),则根据提供的数组类型进行计算(对于 NumPy 数组立即计算,对于 Dask 数组延迟计算)。- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
- 返回:
- 出ndarray 或 dask 数组
返回应用操作的结果。类型取决于
compute参数。
注释
Numpy 的边缘模式 ‘symmetric’、’wrap’ 和 ‘edge’ 分别转换为等效的
dask边界模式 ‘reflect’、’periodic’ 和 ‘nearest’。设置compute=False对于链接后续操作非常有用。例如,区域选择以预览结果或将大数据存储到磁盘而不是加载到内存中。
- skimage.util.compare_images(image0, image1, *, method='diff', n_tiles=(8, 8))[源代码][源代码]#
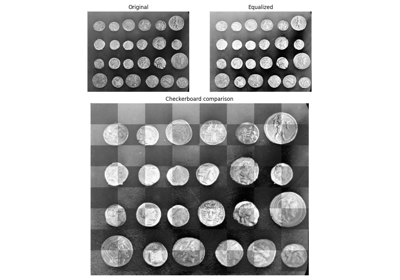
返回一张显示两张图片之间差异的图片。
Added in version 0.16.
- 参数:
- image0, image1ndarray, 形状 (M, N)
要处理的图像,必须具有相同的形状。
在 0.24 版本发生变更: image1 和 image2 分别被重命名为 image0 和 image1。
- 方法字符串,可选
用于比较的方法。有效值为 {‘diff’, ‘blend’, ‘checkerboard’}。详细信息在注释部分提供。
在 0.24 版本发生变更: 此参数及后续参数仅限关键字。
- n_tilestuple, 可选
仅用于 checkerboard 方法。指定将图像分割成的瓦片数量(行,列)。
- 返回:
- 比较ndarray, 形状 (M, N)
显示差异的图像。
注释
'diff'计算两幅图像之间的绝对差异。'blend'计算平均值。'checkerboard'创建尺寸为 n_tiles 的瓦片,交替显示第一幅和第二幅图像。请注意,图像必须是二维的,才能使用棋盘格方法进行比较。
- skimage.util.crop(ar, crop_width, copy=False, order='K')[源代码][源代码]#
沿每个维度裁剪数组 ar 的 crop_width。
- 参数:
- arN 秩的类数组
输入数组。
- crop_width{序列, 整数}
从每个轴的边缘移除的值的数量。
((before_1, after_1),…(before_N, after_N))为每个轴的开始和结束指定唯一的裁剪宽度。((before, after),) 或 (before, after)为每个轴指定固定的开始和结束裁剪。(n,)或n对于整数n是所有轴的 before = after =n的快捷方式。- 复制bool, 可选
如果 True,确保返回的数组是一个连续的副本。通常,裁剪操作将返回底层输入数组的一个不连续视图。
- 顺序{‘C’, ‘F’, ‘A’, ‘K’}, 可选
如果
copy==True,控制副本的内存布局。参见np.copy。
- 返回:
- 裁剪数组
裁剪后的数组。如果 ``copy=False``(默认),这是输入数组的切片视图。
- skimage.util.dtype_limits(image, clip_negative=False)[源代码][源代码]#
返回图像数据类型的强度限制,即 (最小值, 最大值) 元组。
- 参数:
- 图像ndarray
输入图像。
- clip_negativebool, 可选
如果为 True,则裁剪负值范围(即返回最小强度为 0),即使图像数据类型允许负值。
- 返回:
- imin, imax元组
低强度和高强度限制。
- skimage.util.img_as_bool(image, force_copy=False)[源代码][源代码]#
将图像转换为布尔格式。
- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- out : bool 类型的 ndarray (bool_)布尔类型的 ndarray (
输出图像。
注释
输入 dtype 的正数范围的上半部分为 True,下半部分为 False。所有负值(如果存在)均为 False。
- skimage.util.img_as_float(image, force_copy=False)[源代码][源代码]#
将图像转换为浮点格式。
此函数类似于
img_as_float64,但不会将低精度浮点数组转换为 float64。- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- 出浮点数 ndarray
输出图像。
注释
浮点图像的范围在从无符号或带符号数据类型转换时分别为 [0.0, 1.0] 或 [-1.0, 1.0]。如果输入图像是浮点类型,强度值不会被修改,并且可以在范围 [0.0, 1.0] 或 [-1.0, 1.0] 之外。
- skimage.util.img_as_float32(image, force_copy=False)[源代码][源代码]#
将图像转换为单精度(32位)浮点格式。
- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- 出float32 的 ndarray
输出图像。
注释
浮点图像的范围在从无符号或带符号数据类型转换时分别为 [0.0, 1.0] 或 [-1.0, 1.0]。如果输入图像是浮点类型,强度值不会被修改,并且可以在范围 [0.0, 1.0] 或 [-1.0, 1.0] 之外。
- skimage.util.img_as_float64(image, force_copy=False)[源代码][源代码]#
将图像转换为双精度(64位)浮点格式。
- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- 出float64 的 ndarray
输出图像。
注释
浮点图像的范围在从无符号或带符号数据类型转换时分别为 [0.0, 1.0] 或 [-1.0, 1.0]。如果输入图像是浮点类型,强度值不会被修改,并且可以在范围 [0.0, 1.0] 或 [-1.0, 1.0] 之外。
- skimage.util.img_as_int(image, force_copy=False)[源代码][源代码]#
将图像转换为16位有符号整数格式。
- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- 出int16 的 ndarray
输出图像。
注释
这些值在 -32768 和 32767 之间缩放。如果输入数据类型是仅正数(例如,uint8),那么输出图像仍然只包含正数值。
- skimage.util.img_as_ubyte(image, force_copy=False)[源代码][源代码]#
将图像转换为8位无符号整数格式。
- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- 出ubyte (uint8) 的 ndarray
输出图像。
注释
负输入值将被裁剪。正数值将在0到255之间缩放。
- skimage.util.img_as_uint(image, force_copy=False)[源代码][源代码]#
将图像转换为16位无符号整数格式。
- 参数:
- 图像ndarray
输入图像。
- 强制复制bool, 可选
强制复制数据,无论其当前的 dtype 如何。
- 返回:
- 出uint16 的 ndarray
输出图像。
注释
负输入值将被裁剪。正值将在0到65535之间缩放。
- skimage.util.invert(image, signed_float=False)[源代码][源代码]#
反转图像。
反转输入图像的强度范围,使得数据类型的最大值变为最小值,反之亦然。此操作根据输入数据类型的不同略有不同:
无符号整数:从数据类型最大值中减去图像
有符号整数:从 -1 中减去图像(参见注释)
浮点数:如果 signed_float 为 False(我们假设图像是无符号的),则从 1 中减去图像;如果 signed_float 为 True,则从 0 中减去图像。
请参阅示例以获得澄清。
- 参数:
- 图像ndarray
输入图像。
- signed_floatbool, 可选
如果为 True 且图像类型为浮点数,则范围假定为 [-1, 1]。如果为 False 且图像类型为浮点数,则范围假定为 [0, 1]。
- 返回:
- 倒置的ndarray
倒置图像。
注释
理想情况下,对于有符号整数,我们只需乘以 -1。然而,有符号整数范围是不对称的。例如,对于 np.int8,可能的值范围是 [-128, 127],因此 -128 * -1 等于 -128!通过从 -1 中减去,我们正确地将最大数据类型值映射到最小值。
示例
>>> img = np.array([[100, 0, 200], ... [ 0, 50, 0], ... [ 30, 0, 255]], np.uint8) >>> invert(img) array([[155, 255, 55], [255, 205, 255], [225, 255, 0]], dtype=uint8) >>> img2 = np.array([[ -2, 0, -128], ... [127, 0, 5]], np.int8) >>> invert(img2) array([[ 1, -1, 127], [-128, -1, -6]], dtype=int8) >>> img3 = np.array([[ 0., 1., 0.5, 0.75]]) >>> invert(img3) array([[1. , 0. , 0.5 , 0.25]]) >>> img4 = np.array([[ 0., 1., -1., -0.25]]) >>> invert(img4, signed_float=True) array([[-0. , -1. , 1. , 0.25]])
- skimage.util.label_points(coords, output_shape)[源代码][源代码]#
为图像掩码上的坐标分配唯一的整数标签
- 参数:
- coords: ndarray
一个包含N个维度为D的坐标的数组
- output_shape: tuple
在 coords 被标记的遮罩的形状
- 返回:
- 标签: ndarray
一个包含 coords 处唯一整数标签的零掩码
注释
标签被分配给转换为整数并从0开始的坐标。
超出掩码范围的坐标会引发 IndexError。
负坐标会引发 ValueError
示例
>>> import numpy as np >>> from skimage.util._label import label_points >>> coords = np.array([[0, 1], [2, 2]]) >>> output_shape = (5, 5) >>> mask = label_points(coords, output_shape) >>> mask array([[0, 1, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 2, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]], dtype=uint64)
- skimage.util.lookfor(what)[源代码][源代码]#
在 scikit-image 文档字符串中进行关键词搜索并打印结果。
警告
此函数可能还会打印不属于 scikit-image 公共 API 的结果。
- 参数:
- 什么str
要查找的词语。
示例
>>> import skimage as ski >>> ski.util.lookfor('regular_grid') Search results for 'regular_grid' --------------------------------- skimage.util.regular_grid Find `n_points` regularly spaced along `ar_shape`. skimage.util.lookfor Do a keyword search on scikit-image docstrings and print results.
- skimage.util.map_array(input_arr, input_vals, output_vals, out=None)[源代码][源代码]#
将输入数组 input_vals 中的值映射到 output_vals。
- 参数:
- input_arr整数数组,形状 (M[, …])
输入标签图像。
- input_vals整数数组,形状为 (K,)
要映射的值。
- 输出值数组,形状 (K,)
要映射到的值。
- 输出: 数组, 形状与 `input_arr` 相同
输出数组。如果未提供,将会创建。它应该与 output_vals 具有相同的 dtype。
- 返回:
- out : 数组, 与 input_arr 形状相同数组,形状相同
映射值的数组。
注释
如果 input_arr 包含 input_vals 未涵盖的值,则这些值将被设置为 0。
示例
>>> import numpy as np >>> import skimage as ski >>> ski.util.map_array( ... input_arr=np.array([[0, 2, 2, 0], [3, 4, 5, 0]]), ... input_vals=np.array([1, 2, 3, 4, 6]), ... output_vals=np.array([6, 7, 8, 9, 10]), ... ) array([[0, 7, 7, 0], [8, 9, 0, 0]])
- skimage.util.montage(arr_in, fill='mean', rescale_intensity=False, grid_shape=None, padding_width=0, *, channel_axis=None)[源代码][源代码]#
创建一个由多个单通道或多通道图像组成的蒙太奇。
从表示一组形状相同的单通道(灰度)或多通道(彩色)图像的输入数组创建一个矩形蒙太奇。
例如,使用以下 arr_in 调用
montage(arr_in)toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。2
3
将返回
toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。2
3
其中 ‘*’ 补丁将由 fill 参数决定。
- 参数:
- arr_inndarray, 形状 (K, M, N[, C])
一个表示形状相同的 K 张图像的集合的数组。
- 填充浮点数或浮点数数组或 ‘mean’,可选
用于填充输出数组中的填充区域和/或额外图块的值。对于单通道集合,必须是 float。对于多通道集合,必须是形状为通道数的类数组对象。如果为 mean,则使用所有图像的平均值。
- rescale_intensitybool, 可选
是否将每张图像的强度重新缩放到 [0, 1]。
- grid_shapetuple, 可选
蒙太奇所需的网格形状 (ntiles_row, ntiles_column)。默认的纵横比是正方形。
- padding_widthint, 可选
瓷砖之间的间距大小以及瓷砖与边框之间的间距。如果不为零,可以使单个图像的边界更容易察觉。
- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
- 返回:
- arr_out(K*(M+p)+p, K*(N+p)+p[, C]) ndarray
输出一个数组,其中包含粘合在一起的输入图像(包括填充 p)。
示例
>>> import numpy as np >>> from skimage.util import montage >>> arr_in = np.arange(3 * 2 * 2).reshape(3, 2, 2) >>> arr_in array([[[ 0, 1], [ 2, 3]], [[ 4, 5], [ 6, 7]], [[ 8, 9], [10, 11]]]) >>> arr_out = montage(arr_in) >>> arr_out.shape (4, 4) >>> arr_out array([[ 0, 1, 4, 5], [ 2, 3, 6, 7], [ 8, 9, 5, 5], [10, 11, 5, 5]]) >>> arr_in.mean() 5.5 >>> arr_out_nonsquare = montage(arr_in, grid_shape=(1, 3)) >>> arr_out_nonsquare array([[ 0, 1, 4, 5, 8, 9], [ 2, 3, 6, 7, 10, 11]]) >>> arr_out_nonsquare.shape (2, 6)
- skimage.util.random_noise(image, mode='gaussian', rng=None, clip=True, **kwargs)[源代码][源代码]#
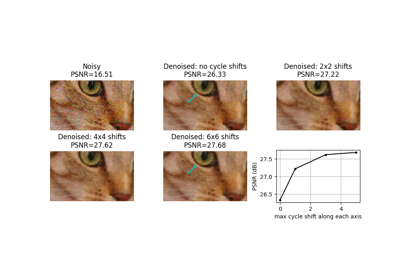
向浮点图像添加各种类型随机噪声的函数。
- 参数:
- 图像ndarray
输入图像数据。将被转换为浮点数。
- 模式str, 可选
从以下字符串中选择要添加的噪声类型:
- ‘gaussian’ (默认)
高斯分布的加性噪声。
- ‘localvar’
高斯分布的加性噪声,在 image 的每个点上具有指定的局部方差。
- ‘泊松’
从数据生成的泊松分布噪声。
- ‘盐’
将随机像素替换为1。
- ‘胡椒’
用0(对于无符号图像)或-1(对于有符号图像)替换随机像素。
- ‘s&p’
将随机像素替换为 1 或 low_val,其中 low_val 对于无符号图像为 0,对于有符号图像为 -1。
- ‘speckle’
使用
out = image + n * image的乘性噪声,其中n是具有指定均值和方差的正态分布噪声。
- rng : {
numpy.random.Generator, int}, 可选toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。 伪随机数生成器。默认情况下,使用 PCG64 生成器(参见
numpy.random.default_rng())。如果 rng 是整数,则用于为生成器设定种子。- 剪辑bool, 可选
如果为 True(默认),在应用 ‘speckle’、’poisson’ 和 ‘gaussian’ 模式后,输出将被裁剪。这是为了保持适当的图像数据范围。如果为 False,则不应用裁剪,输出可能会超出范围 [-1, 1]。
- 平均float, 可选
随机分布的均值。用于 ‘gaussian’ 和 ‘speckle’。默认值:0。
- 变量float, 可选
随机分布的方差。用于 ‘gaussian’ 和 ‘speckle’。注意:方差 = (标准差) ** 2。默认值:0.01
- local_varsndarray,可选
正浮点数数组,形状与 image 相同,定义了图像中每一点的局部方差。用于 ‘localvar’。
- 金额float, 可选
图像像素被噪声替换的比例,范围为 [0, 1]。用于 ‘salt’, ‘pepper’, 和 ‘salt & pepper’。默认值:0.05
- 盐_vs_胡椒float, 可选
在范围 [0, 1] 上,’s&p’ 的盐与胡椒噪声的比例。值越高代表盐越多。默认值:0.5(相等数量)
- 返回:
- 出ndarray
在范围 [0, 1] 或 [-1, 1] 上输出浮点图像数据,如果输入 image 是无符号或有符号的,分别对应。
注释
Speckle、Poisson、Localvar 和 Gaussian 噪声可能会在有效图像范围之外生成噪声。默认情况下会裁剪(不进行别名处理)这些值,但可以通过设置 clip=False 来保留它们。请注意,在这种情况下,输出可能包含超出范围 [0, 1] 或 [-1, 1] 的值。请谨慎使用此选项。
由于中间计算中普遍存在仅正浮点图像,仅根据 dtype 无法判断输入是否为有符号。因此,需要显式搜索负值。只有在找到负值时,此函数才会假定输入为有符号。意外结果仅在罕见、曝光不良的情况下发生(例如,如果有符号 image 中的所有值都高于 50% 灰度)。在这种情况下,手动将输入缩放到正域将解决问题。
泊松分布仅针对正整数定义。要应用这种噪声类型,首先找到图像中唯一值的数量,然后使用下一个二的幂来放大浮点结果,之后再将其缩小回浮点图像范围。
为了在有符号图像上生成泊松噪声,有符号图像会暂时转换为浮点域中的无符号图像,生成泊松噪声,然后返回到原始范围。
- skimage.util.regular_grid(ar_shape, n_points)[源代码][源代码]#
在 ar_shape 上找到 n_points 个等间距的点。
返回的点(作为切片)应尽可能接近立方体间隔。本质上,这些点的间隔是输入数组大小的N次根,其中N是维数。然而,如果数组维度不能容纳完整的步长,则该维度被“丢弃”,计算仅针对剩余的维度进行。
- 参数:
- ar_shape类数组的整数
嵌入网格的空间形状。
len(ar_shape)是维度的数量。- n_points整数
要嵌入到空间中的(近似)点数。
- 返回:
- 切片切片对象的元组
沿着 ar_shape 的每个维度进行切片,使得所有切片的交集给出规则间隔点的坐标。
在 0.14.1 版本发生变更: 在 scikit-image 0.14.1 和 0.15 版本中,返回类型从列表更改为元组,以确保 与 Numpy 1.15 及以上版本的兼容性。如果你的代码需要返回结果为列表,你可以使用以下方法将此函数的输出转换为列表:
>>> result = list(regular_grid(ar_shape=(3, 20, 40), n_points=8))
示例
>>> ar = np.zeros((20, 40)) >>> g = regular_grid(ar.shape, 8) >>> g (slice(5, None, 10), slice(5, None, 10)) >>> ar[g] = 1 >>> ar.sum() 8.0 >>> ar = np.zeros((20, 40)) >>> g = regular_grid(ar.shape, 32) >>> g (slice(2, None, 5), slice(2, None, 5)) >>> ar[g] = 1 >>> ar.sum() 32.0 >>> ar = np.zeros((3, 20, 40)) >>> g = regular_grid(ar.shape, 8) >>> g (slice(1, None, 3), slice(5, None, 10), slice(5, None, 10)) >>> ar[g] = 1 >>> ar.sum() 8.0
- skimage.util.regular_seeds(ar_shape, n_points, dtype=<class 'int'>)[源代码][源代码]#
返回一张包含 ~`n_points` 个等间距非零像素的图像。
- 参数:
- ar_shapeint 的元组
所需输出图像的形状。
- n_points整数
所需的非零点数量。
- dtypenumpy 数据类型,可选
输出所需的数据类型。
- 返回:
- seed_imgint 或 bool 的数组
所需的图像。
示例
>>> regular_seeds((5, 5), 4) array([[0, 0, 0, 0, 0], [0, 1, 0, 2, 0], [0, 0, 0, 0, 0], [0, 3, 0, 4, 0], [0, 0, 0, 0, 0]])
- skimage.util.slice_along_axes(image, slices, axes=None, copy=False)[源代码][源代码]#
沿给定轴切割图像。
- 参数:
- 图像ndarray
输入图像。
- 切片2-元组列表 (a, b) 其中 a < b。
对于 axes 中的每个轴,使用相应的 2-元组
(min_val, max_val)进行切片(与 Python 切片一样,max_val是不包含的)。- 轴int 或 tuple,可选
对应于 slices 中给定限制的轴。如果为 None,则轴按升序排列,最多到 slices 的长度。
- 复制bool, 可选
如果为真,确保输出不是 image 的视图。
- 返回:
- 出ndarray
与给定切片和轴对应的 图像 区域。
示例
>>> from skimage import data >>> img = data.camera() >>> img.shape (512, 512) >>> cropped_img = slice_along_axes(img, [(0, 100)]) >>> cropped_img.shape (100, 512) >>> cropped_img = slice_along_axes(img, [(0, 100), (0, 100)]) >>> cropped_img.shape (100, 100) >>> cropped_img = slice_along_axes(img, [(0, 100), (0, 75)], axes=[1, 0]) >>> cropped_img.shape (75, 100)
- skimage.util.unique_rows(ar)[源代码][源代码]#
从二维数组中移除重复的行。
特别是,如果给定一个形状为 (Npoints, Ndim) 的坐标数组,它将移除重复的点。
- 参数:
- arndarray, 形状 (M, N)
输入数组。
- 返回:
- ar_outndarray, 形状 (P, N)
输入数组的副本,删除了重复的行。
- Raises:
- ValueError : 如果 ar 不是二维的。如果
注释
如果 ar 不是 C 连续的,该函数将生成一个副本,这会对大型输入数组的性能产生负面影响。
示例
>>> ar = np.array([[1, 0, 1], ... [0, 1, 0], ... [1, 0, 1]], np.uint8) >>> unique_rows(ar) array([[0, 1, 0], [1, 0, 1]], dtype=uint8)
- skimage.util.view_as_blocks(arr_in, block_shape)[源代码][源代码]#
输入 n 维数组的块视图(使用重新分块)。
块是输入数组的非重叠视图。
- 参数:
- arr_inndarray, 形状 (M[, …])
输入数组。
- block_shape元组
块的形状。每个维度必须均匀地划分 arr_in 的相应维度。
- 返回:
- arr_outndarray
输入数组的块视图。
示例
>>> import numpy as np >>> from skimage.util.shape import view_as_blocks >>> A = np.arange(4*4).reshape(4,4) >>> A array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15]]) >>> B = view_as_blocks(A, block_shape=(2, 2)) >>> B[0, 0] array([[0, 1], [4, 5]]) >>> B[0, 1] array([[2, 3], [6, 7]]) >>> B[1, 0, 1, 1] 13
>>> A = np.arange(4*4*6).reshape(4,4,6) >>> A array([[[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [18, 19, 20, 21, 22, 23]], [[24, 25, 26, 27, 28, 29], [30, 31, 32, 33, 34, 35], [36, 37, 38, 39, 40, 41], [42, 43, 44, 45, 46, 47]], [[48, 49, 50, 51, 52, 53], [54, 55, 56, 57, 58, 59], [60, 61, 62, 63, 64, 65], [66, 67, 68, 69, 70, 71]], [[72, 73, 74, 75, 76, 77], [78, 79, 80, 81, 82, 83], [84, 85, 86, 87, 88, 89], [90, 91, 92, 93, 94, 95]]]) >>> B = view_as_blocks(A, block_shape=(1, 2, 2)) >>> B.shape (4, 2, 3, 1, 2, 2) >>> B[2:, 0, 2] array([[[[52, 53], [58, 59]]], [[[76, 77], [82, 83]]]])
- skimage.util.view_as_windows(arr_in, window_shape, step=1)[源代码][源代码]#
输入 n 维数组的滚动窗口视图。
窗口是输入数组的叠加视图,相邻窗口按单行或单列(或更高维度的索引)移动。
- 参数:
- arr_inndarray, 形状 (M[, …])
输入数组。
- 窗口形状整数或长度为 arr_in.ndim 的元组
定义滚动窗口视图的基本 n 维正交多面体(更广为人知的名称是超矩形 [1])的形状。如果给定一个整数,形状将是一个边长为其值的超立方体。
- 步骤整数或长度为 arr_in.ndim 的元组
指示执行提取的步长。如果给定整数,则所有维度中的步长是均匀的。
- 返回:
- arr_outndarray
(滚动) 窗口视图的输入数组。
注释
在使用滚动视图时,应非常小心内存的使用。确实,尽管’视图’与其基础数组具有相同的内存占用,但在计算中使用此’视图’时出现的实际数组通常比原始数组大得多,尤其是对于二维及以上的数组。
例如,让我们考虑一个大小为 (100, 100, 100) 的
float64三维数组。该数组大约占用 8*100**3 字节的存储空间,即 8 MB。如果决定在这个数组上构建一个窗口为 (3, 3, 3) 的滚动视图,那么滚动视图的假设大小(例如,如果要对视图进行重塑)将是 8*(100-3+1)**3*3**3,大约为 203 MB!随着输入数组维度的增加,这种缩放变得更加糟糕。参考文献
示例
>>> import numpy as np >>> from skimage.util.shape import view_as_windows >>> A = np.arange(4*4).reshape(4,4) >>> A array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15]]) >>> window_shape = (2, 2) >>> B = view_as_windows(A, window_shape) >>> B[0, 0] array([[0, 1], [4, 5]]) >>> B[0, 1] array([[1, 2], [5, 6]])
>>> A = np.arange(10) >>> A array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) >>> window_shape = (3,) >>> B = view_as_windows(A, window_shape) >>> B.shape (8, 3) >>> B array([[0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4, 5], [4, 5, 6], [5, 6, 7], [6, 7, 8], [7, 8, 9]])
>>> A = np.arange(5*4).reshape(5, 4) >>> A array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15], [16, 17, 18, 19]]) >>> window_shape = (4, 3) >>> B = view_as_windows(A, window_shape) >>> B.shape (2, 2, 4, 3) >>> B array([[[[ 0, 1, 2], [ 4, 5, 6], [ 8, 9, 10], [12, 13, 14]], [[ 1, 2, 3], [ 5, 6, 7], [ 9, 10, 11], [13, 14, 15]]], [[[ 4, 5, 6], [ 8, 9, 10], [12, 13, 14], [16, 17, 18]], [[ 5, 6, 7], [ 9, 10, 11], [13, 14, 15], [17, 18, 19]]]])