skimage.segmentation#
将图像分割成有意义的区域或边界的算法。
活动轮廓模型。 |
|
Chan-Vese 分割算法。 |
|
创建一个具有二进制值的棋盘格水平集。 |
|
清除连接到标签图像边界的对象。 |
|
创建一个具有二进制值的磁盘级别集。 |
|
在不重叠的情况下,将标签图像中的标签扩展 |
|
计算基于Felsenszwalb的高效图图像分割。 |
|
返回一个布尔数组,其中标记区域之间的边界为 True。 |
|
对应于泛洪填充的掩码。 |
|
对图像执行填充操作。 |
|
梯度幅度的逆。 |
|
返回两个输入分段的连接结果。 |
|
返回带有标记区域之间边界高亮的图像。 |
|
无边缘的形态学活动轮廓 (MorphACWE) |
|
形态学测地活动轮廓 (MorphGAC)。 |
|
在颜色-(x,y)空间中使用quickshift聚类进行图像分割。 |
|
基于标记的分割随机游走算法。 |
|
将任意标签重新标记为 {offset, . |
|
使用颜色-(x,y,z)空间中的k-means聚类对图像进行分割。 |
|
在从给定标记淹没的图像中找到分水岭盆地。 |
- skimage.segmentation.active_contour(image, snake, alpha=0.01, beta=0.1, w_line=0, w_edge=1, gamma=0.01, max_px_move=1.0, max_num_iter=2500, convergence=0.1, *, boundary_condition='periodic')[源代码][源代码]#
活动轮廓模型。
通过拟合蛇形轮廓到图像特征来实现主动轮廓。支持单通道和多通道的2D图像。蛇形轮廓可以是周期性的(用于分割)或具有固定和/或自由端。输出蛇形轮廓的长度与输入边界相同。由于点的数量是恒定的,请确保初始蛇形轮廓有足够的点来捕捉最终轮廓的细节。
- 参数:
- 图像(M, N) 或 (M, N, 3) ndarray
输入图像。
- 蛇(K, 2) ndarray
初始蛇的坐标。对于周期性边界条件,端点不能重复。
- alphafloat, 可选
蛇的长度形状参数。较高的值使蛇收缩得更快。
- betafloat, 可选
蛇的光滑度形状参数。更高的值使蛇更光滑。
- w_linefloat, 可选
控制对亮度的吸引力。使用负值吸引向暗区域。
- w_edgefloat, 可选
控制对边缘的吸引力。使用负值使蛇远离边缘。
- gammafloat, 可选
显式时间步长参数。
- max_px_movefloat, 可选
每次迭代移动的最大像素距离。
- max_num_iterint, 可选
优化蛇形形状的最大迭代次数。
- 收敛float, 可选
收敛准则。
- 边界条件字符串,可选
轮廓的边界条件。可以是 ‘periodic’、’free’、’fixed’、’free-fixed’ 或 ‘fixed-free’ 之一。’periodic’ 连接蛇的两端,’fixed’ 固定端点,’free’ 允许端点自由移动。’fixed’ 和 ‘free’ 可以通过解析 ‘fixed-free’、’free-fixed’ 来组合。解析 ‘fixed-fixed’ 或 ‘free-free’ 分别产生与 ‘fixed’ 和 ‘free’ 相同的行为。
- 返回:
- 蛇(K, 2) ndarray
优化后的蛇,形状与输入参数相同。
参考文献
[1]Kass, M.; Witkin, A.; Terzopoulos, D. “Snakes: Active contour models”. International Journal of Computer Vision 1 (4): 321 (1988). DOI:10.1007/BF00133570
示例
>>> from skimage.draw import circle_perimeter >>> from skimage.filters import gaussian
创建和平滑图像:
>>> img = np.zeros((100, 100)) >>> rr, cc = circle_perimeter(35, 45, 25) >>> img[rr, cc] = 1 >>> img = gaussian(img, sigma=2, preserve_range=False)
初始化样条线:
>>> s = np.linspace(0, 2*np.pi, 100) >>> init = 50 * np.array([np.sin(s), np.cos(s)]).T + 50
拟合图像的样条曲线:
>>> snake = active_contour(img, init, w_edge=0, w_line=1) >>> dist = np.sqrt((45-snake[:, 0])**2 + (35-snake[:, 1])**2) >>> int(np.mean(dist)) 25
- skimage.segmentation.chan_vese(image, mu=0.25, lambda1=1.0, lambda2=1.0, tol=0.001, max_num_iter=500, dt=0.5, init_level_set='checkerboard', extended_output=False)[源代码][源代码]#
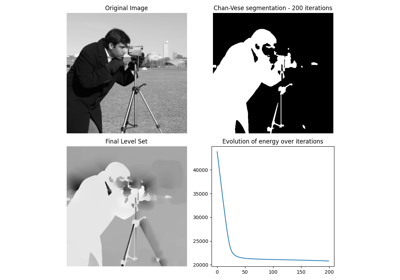
Chan-Vese 分割算法。
通过演化水平集的主动轮廓模型。可用于分割没有清晰定义边界的对象。
- 参数:
- 图像(M, N) ndarray
待分割的灰度图像。
- mufloat, 可选
‘边缘长度’ 权重参数。较高的 mu 值将产生一个 ‘圆’ 边缘,而接近零的值将检测到较小的物体。
- lambda1float, 可选
‘difference from average’ 输出区域的权重参数值为 ‘True’。如果该值低于 lambda2,则此区域的值范围将比其他区域更大。
- lambda2float, 可选
‘difference from average’ 输出区域的权重参数值为 ‘False’。如果它低于 lambda1,该区域的值范围将比其他区域更大。
- tol浮点数, 正数, 可选
迭代之间的水平集变化容差。如果连续迭代之间的水平集的L2范数差值除以图像面积后的值低于此值,算法将认为已达到解决方案。
- max_num_iteruint, 可选
算法在自我中断之前允许的最大迭代次数。
- dtfloat, 可选
在每个步骤的计算中应用的乘法因子,用于加速算法。虽然较高的值可能会加快算法速度,但它们也可能导致收敛问题。
- init_level_setstr 或 (M, N) ndarray,可选
定义算法使用的起始水平集。如果输入的是字符串,将自动生成与图像大小匹配的水平集。或者,可以定义一个自定义水平集,该水平集应为与’image’形状相同的浮点值数组。接受的字符串值如下。
- ‘棋盘’
初始水平集定义为 sin(x/5*pi)*sin(y/5*pi),其中 x 和 y 是像素坐标。该水平集具有快速收敛性,但可能无法检测到隐式边缘。
- ‘磁盘’
起始级别集定义为图像中心距离的相反数减去图像宽度和高度最小值的一半。这稍微慢一些,但更有可能正确检测到隐含的边缘。
- ‘小磁盘’
起始水平集定义为图像中心距离的相反数减去图像宽度和高度最小值的四分之一。
- extended_outputbool, 可选
如果设置为 True,返回值将是一个包含三个返回值的元组(见下文)。如果设置为 False,这是默认值,则只会返回 ‘segmentation’ 数组。
- 返回:
- 分割(M, N) ndarray, bool
算法生成的分割结果。
- phi(M, N) 浮点数 ndarray
算法计算出的最终水平集。
- 能量浮点数列表
显示算法每一步的 ‘能量’ 变化。这应该可以用来检查算法是否收敛。
注释
Chan-Vese算法旨在分割没有清晰定义边界的对象。该算法基于水平集,这些水平集通过迭代演化以最小化能量,该能量由加权值定义,对应于分割区域外平均值的强度差异之和、分割区域内平均值的差异之和,以及依赖于分割区域边界长度的项。
该算法由Tony Chan和Luminita Vese首次提出,发表在题为“一种无边缘的活动轮廓模型”的文章中 [1]。
该算法的实现略有简化,因为在原始论文中描述的面积因子 ‘nu’ 未被实现,并且仅适用于灰度图像。
lambda1 和 lambda2 的典型值为 1。如果 ‘背景’ 在分布上与分割对象非常不同(例如,一张均匀黑色的图像,其中有强度各异的图形),那么这些值应该彼此不同。
mu 的典型值介于 0 和 1 之间,尽管在处理轮廓非常不明确的形状时可以使用更高的值。
该算法试图最小化的’能量’定义为区域内与平均值差异的平方和,并由’lambda’因子加权,再加上轮廓长度乘以’mu’因子。
仅支持2D灰度图像,并且未实现原始文章中描述的区域项。
参考文献
[1]一个没有边缘的活动轮廓模型,Tony Chan 和 Luminita Vese,计算机视觉中的尺度空间理论,1999年,DOI:10.1007/3-540-48236-9_13
[2]Chan-Vese 分割, Pascal Getreuer 图像处理在线, 2 (2012), 页码. 214-224, DOI:10.5201/ipol.2012.g-cv
[3]Chan-Vese算法 - 项目报告, Rami Cohen, 2011 arXiv:1107.2782
- skimage.segmentation.checkerboard_level_set(image_shape, square_size=5)[源代码][源代码]#
创建一个具有二进制值的棋盘格水平集。
- 参数:
- image_shape正整数的元组
图像的形状。
- square_sizeint, 可选
棋盘方格的大小。默认为 5。
- 返回:
- out : 形状为 image_shape 的数组具有形状的数组
棋盘格的二进制水平集。
- skimage.segmentation.clear_border(labels, buffer_size=0, bgval=0, mask=None, *, out=None)[源代码][源代码]#
清除连接到标签图像边界的对象。
- 参数:
- 标签(M[, N[, …, P]]) 的 int 或 bool 数组
成像数据标签。
- buffer_sizeint, 可选
检查的边框宽度。默认情况下,只有接触图像外部的对象才会被移除。
- bgval浮点数或整数,可选
已清除的对象被设置为此值。
- mask : 布尔类型的 ndarray, 形状与 image 相同, 可选。布尔类型的 ndarray,形状与
图像数据掩码。标签图像中与掩码的 False 像素重叠的对象将被移除。如果定义了,参数 buffer_size 将被忽略。
- 出ndarray
与 labels 形状相同的数组,输出将被放置在其中。默认情况下,会创建一个新的数组。
- 返回:
- 出(M[, N[, …, P]]) 数组
带有清晰边界的成像数据标签
示例
>>> import numpy as np >>> from skimage.segmentation import clear_border >>> labels = np.array([[0, 0, 0, 0, 0, 0, 0, 1, 0], ... [1, 1, 0, 0, 1, 0, 0, 1, 0], ... [1, 1, 0, 1, 0, 1, 0, 0, 0], ... [0, 0, 0, 1, 1, 1, 1, 0, 0], ... [0, 1, 1, 1, 1, 1, 1, 1, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> clear_border(labels) array([[0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]]) >>> mask = np.array([[0, 0, 1, 1, 1, 1, 1, 1, 1], ... [0, 0, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1], ... [1, 1, 1, 1, 1, 1, 1, 1, 1]]).astype(bool) >>> clear_border(labels, mask=mask) array([[0, 0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0, 0, 1, 0], [0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 0, 0], [0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]])
- skimage.segmentation.disk_level_set(image_shape, *, center=None, radius=None)[源代码][源代码]#
创建一个具有二进制值的磁盘级别集。
- 参数:
- image_shape正整数的元组
图像的形状
- 中心正整数的元组,可选
给定在 (行, 列) 中的圆盘中心的坐标。如果未给定,则默认为图像的中心。
- 半径float, 可选
磁盘的半径。如果没有给出,它被设置为最小图像尺寸的75%。
- 返回:
- out : 形状为 image_shape 的数组具有形状的数组
具有给定 radius 和 center 的磁盘的二进制水平集。
- skimage.segmentation.expand_labels(label_image, distance=1, spacing=1)[源代码][源代码]#
在不重叠的情况下,将标签图像中的标签扩展
distance像素。给定一个标签图像,
expand_labels会将标签区域(连通分量)向外扩展最多distance个单位,而不会溢出到相邻区域。更具体地说,每个背景像素如果在连通分量的欧几里得距离 <=distance像素范围内,则会被分配该连通分量的标签。spacing 参数可用于指定用于计算各向异性图像欧几里得距离的距离变换的间距率。如果多个连通分量在distance像素范围内接近一个背景像素,则将分配最接近的连通分量的标签值(参见注释中关于等距离多个标签的情况)。- 参数:
- label_imagedtype 为 int 的 ndarray
标签 图像
- 距离浮动
用于扩展标签的欧几里得距离(以像素为单位)。默认值为1。
- 间距float, 或 float 序列, 可选
每个维度上元素的间距。如果是一个序列,长度必须等于输入的秩;如果是一个单一的数字,这个数字将用于所有轴。如果没有指定,则默认间距为1。
- 返回:
- enlarged_labelsdtype 为 int 的 ndarray
标记数组,其中所有连接区域都已放大
注释
当标签之间的距离超过
distance像素时,这相当于使用半径为distance的圆盘或超球进行形态学膨胀。然而,与形态学膨胀不同,expand_labels不会将标签区域扩展到相邻区域。这个
expand_labels的实现源自 CellProfiler [1],在那里它被称为模块 “IdentifySecondaryObjects (Distance-N)” [2]。当一个像素到多个区域的距离相同时,存在一个重要的边缘情况,因为不确定哪个区域会扩展到该空间。此时,确切的行为取决于
scipy.ndimage.distance_transform_edt的上游实现。参考文献
示例
>>> labels = np.array([0, 1, 0, 0, 0, 0, 2]) >>> expand_labels(labels, distance=1) array([1, 1, 1, 0, 0, 2, 2])
标签不会相互覆盖:
>>> expand_labels(labels, distance=3) array([1, 1, 1, 1, 2, 2, 2])
在平局的情况下,行为未定义,但目前会解析为在字典顺序上最接近
(0,) * ndim的标签。>>> labels_tied = np.array([0, 1, 0, 2, 0]) >>> expand_labels(labels_tied, 1) array([1, 1, 1, 2, 2]) >>> labels2d = np.array( ... [[0, 1, 0, 0], ... [2, 0, 0, 0], ... [0, 3, 0, 0]] ... ) >>> expand_labels(labels2d, 1) array([[2, 1, 1, 0], [2, 2, 0, 0], [2, 3, 3, 0]]) >>> expand_labels(labels2d, 1, spacing=[1, 0.5]) array([[1, 1, 1, 1], [2, 2, 2, 0], [3, 3, 3, 3]])
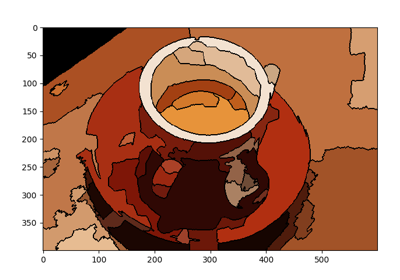
- skimage.segmentation.felzenszwalb(image, scale=1, sigma=0.8, min_size=20, *, channel_axis=-1)[源代码][源代码]#
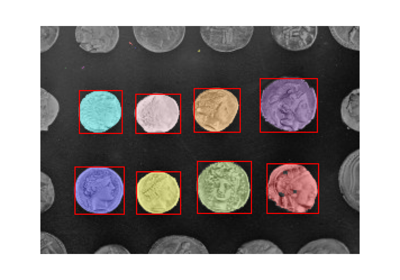
计算基于Felsenszwalb的高效图图像分割。
使用基于图像网格的快速最小生成树聚类,对多通道(即RGB)图像进行过分割。参数
scale设置观察级别。更高的比例意味着更少且更大的片段。sigma是高斯核的直径,用于在分割前平滑图像。生成的片段数量及其大小只能通过
scale间接控制。图像中片段的大小会根据局部对比度而有很大差异。对于RGB图像,该算法使用颜色空间中像素之间的欧几里得距离。
- 参数:
- 图像(M, N[, 3]) ndarray
输入图像。
- 比例浮动
自由参数。数值越高意味着更大的簇。
- sigma浮动
高斯核在预处理中使用的宽度(标准差)。
- min_size整数
最小组件尺寸。通过后处理强制执行。
- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19:
channel_axis在 0.19 版本中被添加。
- 返回:
- segment_mask(M, N) ndarray
整数掩码,指示段落标签。
注释
原始论文中使用的 k 参数在这里被重命名为 scale。
参考文献
[1]基于图的高效图像分割,Felzenszwalb, P.F. 和 Huttenlocher, D.P. 国际计算机视觉杂志,2004
示例
>>> from skimage.segmentation import felzenszwalb >>> from skimage.data import coffee >>> img = coffee() >>> segments = felzenszwalb(img, scale=3.0, sigma=0.95, min_size=5)
- skimage.segmentation.find_boundaries(label_img, connectivity=1, mode='thick', background=0)[源代码][源代码]#
返回一个布尔数组,其中标记区域之间的边界为 True。
- 参数:
- label_imgint 或 bool 的数组
一个数组,其中不同的区域被标记为不同的整数或布尔值。
- 连通性 : int in {1, …, label_img.ndim}, 可选int in {1, …,
如果一个像素的任何邻居具有不同的标签,则该像素被视为边界像素。connectivity 控制哪些像素被视为邻居。连接性为 1(默认)意味着共享一条边(在2D中)或一个面(在3D中)的像素将被视为邻居。连接性为 label_img.ndim 意味着共享一个角的像素将被视为邻居。
- 模式字符串 in {‘thick’, ‘inner’, ‘outer’, ‘subpixel’}
如何标记边界:
thick: 任何未被相同标签像素完全包围的像素(由 connectivity 定义)都被标记为边界。这会导致边界厚度为2个像素。
inner: 勾勒对象*内部*的像素,保持背景像素不变。
outer: 在对象边界周围的背景中勾勒像素。当两个对象接触时,它们的边界也会被标记。
subpixel: 返回一个双倍大小的图像,其中原始像素之间的像素在适当的位置标记为边界。
- 背景int, 可选
对于模式 ‘inner’ 和 ‘outer’,需要定义一个背景标签。有关这两种模式的描述,请参见 mode。
- 返回:
- boundaries : 布尔数组,形状与 label_img 相同布尔数组,形状相同
一个布尔图像,其中
True表示边界像素。对于 mode 等于 ‘subpixel’,boundaries.shape[i]等于2 * label_img.shape[i] - 1对于所有 ``i``(在所有其他像素对之间插入一个像素)。
示例
>>> labels = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 1, 1, 1, 5, 5, 5, 0, 0], ... [0, 0, 0, 0, 0, 5, 5, 5, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=np.uint8) >>> find_boundaries(labels, mode='thick').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1, 1, 0], [0, 1, 1, 0, 1, 1, 0, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0, 1, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels, mode='inner').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [0, 0, 1, 0, 1, 1, 0, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels, mode='outer').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 1, 0, 0, 1, 0], [0, 0, 1, 1, 1, 1, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> labels_small = labels[::2, ::3] >>> labels_small array([[0, 0, 0, 0], [0, 0, 5, 0], [0, 1, 5, 0], [0, 0, 5, 0], [0, 0, 0, 0]], dtype=uint8) >>> find_boundaries(labels_small, mode='subpixel').astype(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 1, 0], [0, 1, 0, 1, 0, 1, 0], [0, 1, 1, 1, 0, 1, 0], [0, 0, 0, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> bool_image = np.array([[False, False, False, False, False], ... [False, False, False, False, False], ... [False, False, True, True, True], ... [False, False, True, True, True], ... [False, False, True, True, True]], ... dtype=bool) >>> find_boundaries(bool_image) array([[False, False, False, False, False], [False, False, True, True, True], [False, True, True, True, True], [False, True, True, False, False], [False, True, True, False, False]])
- skimage.segmentation.flood(image, seed_point, *, footprint=None, connectivity=None, tolerance=None)[源代码][源代码]#
对应于泛洪填充的掩码。
从特定的 seed_point 开始,找到与种子值相等或在 tolerance 范围内的相连点。
- 参数:
- 图像ndarray
一个n维数组。
- seed_point元组或整数
用于 image 中作为泛洪填充起始点的点。如果图像是1D的,这个点可以作为一个整数给出。
- 足迹ndarray,可选
用于确定每个评估像素邻域的足迹(结构元素)。它必须仅包含1和0,并且与`image`具有相同的维度数。如果未给出,则所有相邻像素都被视为邻域的一部分(完全连接)。
- 连接性int, 可选
用于确定每个评估像素邻域的数值。与中心像素的平方距离小于或等于 connectivity 的相邻像素被视为邻居。如果 footprint 不为 None,则忽略此参数。
- 容差浮点数或整数,可选
如果为 None(默认),相邻值必须严格等于 seed_point 处 image 的初始值。这是最快的。如果给定一个值,将在每个点进行比较,如果与初始值在容差范围内也将被填充(包含)。
- 返回:
- 掩码ndarray
返回一个与 image 形状相同的布尔数组,其中与种子点相连且相等(或在容差范围内)的区域值为 True。所有其他值为 False。
注释
这个操作的概念类比是许多光栅图形程序中的’油漆桶’工具。这个函数只返回表示填充的掩码。
如果出于内存原因需要索引而不是掩码,用户可以简单地在结果上运行
numpy.nonzero,保存索引,并丢弃此掩码。示例
>>> from skimage.morphology import flood >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用5填充相连的部分,包括完全连接(包括对角线):
>>> mask = flood(image, (1, 1)) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
填充相连的点为5,不包括对角点(连接性1):
>>> mask = flood(image, (1, 1), connectivity=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
填充具有容差:
>>> mask = flood(image, (0, 0), tolerance=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.segmentation.flood_fill(image, seed_point, new_value, *, footprint=None, connectivity=None, tolerance=None, in_place=False)[源代码][源代码]#
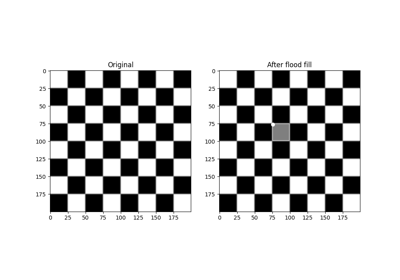
对图像执行填充操作。
从特定的 seed_point 开始,找到与种子值相等或在其 tolerance 范围内的相连点,然后将其设置为 new_value。
- 参数:
- 图像ndarray
一个n维数组。
- seed_point元组或整数
用于 image 中作为泛洪填充起始点的点。如果图像是1D的,这个点可以作为一个整数给出。
- new_value : image 类型图像类型
新值用于设置整个填充。这必须与 image 的 dtype 一致选择。
- 足迹ndarray,可选
用于确定每个评估像素邻域的足迹(结构元素)。它必须仅包含1和0,并且与`image`具有相同的维度数。如果未给出,则所有相邻像素都被视为邻域的一部分(完全连接)。
- 连接性int, 可选
用于确定每个评估像素邻域的数值。与中心像素的平方距离小于或等于 connectivity 的相邻像素被视为邻居。如果 footprint 不为 None,则忽略此参数。
- 容差浮点数或整数,可选
如果为 None(默认),相邻值必须严格等于 seed_point 处的 image 值才能被填充。这是最快的。如果提供了容差,则填充值在种子点值的正负容差范围内的相邻点(包括边界)。
- in_placebool, 可选
如果为 True,则对 image 进行就地泛洪填充。如果为 False,则返回泛洪填充的结果而不修改输入的 `image`(默认)。
- 返回:
- 填充ndarray
返回一个与 image 形状相同的数组,其中与种子点相连且相等(或在容差范围内)的区域值被替换为 new_value。
注释
这个操作的概念类比是许多光栅图形程序中的’油漆桶’工具。
示例
>>> from skimage.morphology import flood_fill >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用5填充相连的部分,包括完全连接(包括对角线):
>>> flood_fill(image, (1, 1), 5) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
填充相连的点为5,不包括对角点(连接性1):
>>> flood_fill(image, (1, 1), 5, connectivity=1) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
填充具有容差:
>>> flood_fill(image, (0, 0), 5, tolerance=1) array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.segmentation.inverse_gaussian_gradient(image, alpha=100.0, sigma=5.0)[源代码][源代码]#
梯度幅度的逆。
计算图像中梯度的大小,然后在范围 [0, 1] 内反转结果。平坦区域被赋予接近 1 的值,而接近边界的区域被赋予接近 0 的值。
此函数或用户定义的类似函数应在调用
morphological_geodesic_active_contour之前作为预处理步骤应用于图像。- 参数:
- 图像(M, N) 或 (L, M, N) 数组
灰度图像或体积。
- alphafloat, 可选
控制反转的陡峭度。较大的值将使结果数组中平坦区域和边界区域之间的过渡更陡峭。
- sigmafloat, 可选
应用于图像的高斯滤波器的标准偏差。
- 返回:
- gimage(M, N) 或 (L, M, N) 数组
预处理图像(或体积)适用于
morphological_geodesic_active_contour。
- skimage.segmentation.join_segmentations(s1, s2, return_mapping: bool = False)[源代码][源代码]#
返回两个输入分段的连接结果。
S1 和 S2 的并集 J 定义为这样的分割:两个体素在同一个段中,当且仅当它们在 S1 和 S2 中都在同一个段中。
- 参数:
- s1, s2numpy 数组
s1 和 s2 是具有相同形状的标签字段。
- return_mappingbool, 可选
如果为真,返回合并分割标签到原始标签的映射。
- 返回:
- jnumpy 数组
s1 和 s2 的连接分割。
- map_j_to_s1ArrayMap,可选
从合并分割 j 的标签映射到 s1 的标签。
- map_j_to_s2ArrayMap,可选
从合并分割 j 的标签映射到 s2 的标签。
示例
>>> from skimage.segmentation import join_segmentations >>> s1 = np.array([[0, 0, 1, 1], ... [0, 2, 1, 1], ... [2, 2, 2, 1]]) >>> s2 = np.array([[0, 1, 1, 0], ... [0, 1, 1, 0], ... [0, 1, 1, 1]]) >>> join_segmentations(s1, s2) array([[0, 1, 3, 2], [0, 5, 3, 2], [4, 5, 5, 3]]) >>> j, m1, m2 = join_segmentations(s1, s2, return_mapping=True) >>> m1 ArrayMap(array([0, 1, 2, 3, 4, 5]), array([0, 0, 1, 1, 2, 2])) >>> np.all(m1[j] == s1) True >>> np.all(m2[j] == s2) True
- skimage.segmentation.mark_boundaries(image, label_img, color=(1, 1, 0), outline_color=None, mode='outer', background_label=0)[源代码][源代码]#
返回带有标记区域之间边界高亮的图像。
- 参数:
- 图像(M, N[, 3]) 数组
灰度或RGB图像。
- label_img(M, N) 的整数数组
标记数组,其中区域由不同的整数值标记。
- 颜色长度为3的序列,可选
输出图像中边界的RGB颜色。
- outline_color长度为3的序列,可选
输出图像中围绕边界的RGB颜色。如果为None,则不绘制轮廓。
- 模式字符串在 {‘thick’, ‘inner’, ‘outer’, ‘subpixel’} 中,可选
查找边界的模式。
- background_labelint, 可选
要考虑的背景标签(这仅对模式
inner和outer有用)。
- 返回:
- 标记(M, N, 3) 的浮点数数组
在原始图像上叠加标签边界的一张图像。
- skimage.segmentation.morphological_chan_vese(image, num_iter, init_level_set='checkerboard', smoothing=1, lambda1=1, lambda2=1, iter_callback=<function <lambda>>)[源代码][源代码]#
无边缘的形态学活动轮廓 (MorphACWE)
使用形态学算子实现的边缘无活动轮廓。它可以用于分割图像和体积中的物体,即使这些物体没有明确的边界。要求物体内部在平均上看起来与外部不同(即,物体的内部区域平均应比外部区域更暗或更亮)。
- 参数:
- 图像(M, N) 或 (L, M, N) 数组
待分割的灰度图像或体积。
- num_iteruint
运行 num_iter 的次数
- init_level_setstr, (M, N) 数组, 或 (L, M, N) 数组
初始化水平集。如果给定一个数组,它将被二值化并作为初始水平集使用。如果给定一个字符串,它定义了生成一个合理初始水平集的方法,该水平集的形状与 image 相同。接受的值为 ‘checkerboard’ 和 ‘disk’。有关这些水平集如何创建的详细信息,请分别参阅
checkerboard_level_set和disk_level_set的文档。- 平滑uint, 可选
每次迭代中应用平滑操作符的次数。合理的值大约在1-4之间。较大的值会导致更平滑的分割。
- lambda1float, 可选
外区域的权重参数。如果 lambda1 大于 lambda2,外区域将包含比内区域更大的数值范围。
- lambda2float, 可选
内部区域的权重参数。如果 lambda2 大于 lambda1,内部区域将包含比外部区域更大的值范围。
- iter_callback函数, 可选
如果提供,此函数将在每次迭代时调用一次,当前级别作为唯一参数。这对于调试或在进化过程中绘制中间结果非常有用。
- 返回:
- 出(M, N) 或 (L, M, N) 数组
最终分割(即,最终水平集)
注释
这是一个使用形态学算子而不是求解偏微分方程(PDE)来演化轮廓的Chan-Vese算法版本。该算法中使用的形态学算子集被证明与Chan-Vese PDE无限等价(参见[R81c856a3d0d3-1]_)。然而,形态学算子不会遭受PDE中常见的数值稳定性问题(不需要为演化找到合适的时间步长),并且计算速度更快。
该算法及其理论推导在 [1] 中描述。
参考文献
[1]基于曲率的曲线和曲面演化的形态学方法,Pablo Márquez-Neila, Luis Baumela, Luis Álvarez. 发表于《IEEE模式分析与机器智能汇刊》(PAMI),2014年,DOI:10.1109/TPAMI.2013.106
- skimage.segmentation.morphological_geodesic_active_contour(gimage, num_iter, init_level_set='disk', smoothing=1, threshold='auto', balloon=0, iter_callback=<function <lambda>>)[源代码][源代码]#
形态学测地活动轮廓 (MorphGAC)。
使用形态学算子的测地活动轮廓。它可以用于分割具有可见但噪声、杂乱、断裂边界的物体。
- 参数:
- gimage(M, N) 或 (L, M, N) 数组
预处理后的图像或体积,用于分割。这很少是原始图像。相反,这通常是原始图像的预处理版本,该版本增强了并突出了要分割对象的边界(或其他结构)。
morphological_geodesic_active_contour()将尝试在 gimage 值小的区域停止轮廓演变。请参阅inverse_gaussian_gradient()作为一个执行此预处理的示例函数。请注意,morphological_geodesic_active_contour()的质量可能很大程度上取决于此预处理。- num_iteruint
要运行的 num_iter 数量。
- init_level_setstr, (M, N) 数组, 或 (L, M, N) 数组
初始化水平集。如果给定一个数组,它将被二值化并作为初始水平集使用。如果给定一个字符串,它定义了生成一个合理初始水平集的方法,该水平集的形状与 image 相同。接受的值为 ‘checkerboard’ 和 ‘disk’。有关这些水平集如何创建的详细信息,请分别参阅
checkerboard_level_set和disk_level_set的文档。- 平滑uint, 可选
每次迭代中应用平滑操作符的次数。合理的值大约在1-4之间。较大的值会导致更平滑的分割。
- 阈值float, 可选
图像中值小于此阈值的区域将被视为边界。轮廓的演化将在这些区域停止。
- 气球float, 可选
在图像的非信息区域引导轮廓的气球力,即图像梯度太小以至于无法将轮廓推向边界的区域。负值将收缩轮廓,而正值将在这些区域扩展轮廓。将其设置为零将禁用气球力。
- iter_callback函数, 可选
如果提供,此函数将在每次迭代时调用一次,当前级别作为唯一参数。这对于调试或在进化过程中绘制中间结果非常有用。
- 返回:
- 出(M, N) 或 (L, M, N) 数组
最终分割(即,最终水平集)
注释
这是一个使用形态学算子而不是求解偏微分方程(PDEs)来演化轮廓的测地活动轮廓(GAC)算法版本。该算法中使用的形态学算子集被证明与GAC PDEs无限等价(参见[Rb6daaf5d7730-1]_)。然而,形态学算子不会遭受PDEs中常见的数值稳定性问题(例如,不需要为演化找到合适的时间步长),并且在计算上更快。
该算法及其理论推导在 [1] 中描述。
参考文献
[1]基于曲率的曲线和曲面演化的形态学方法,Pablo Márquez-Neila, Luis Baumela, Luis Álvarez. 发表于《IEEE模式分析与机器智能汇刊》(PAMI),2014年,DOI:10.1109/TPAMI.2013.106
- skimage.segmentation.quickshift(image, ratio=1.0, kernel_size=5, max_dist=10, return_tree=False, sigma=0, convert2lab=True, rng=42, *, channel_axis=-1)[源代码][源代码]#
在颜色-(x,y)空间中使用quickshift聚类进行图像分割。
使用快速移位模式搜索算法生成图像的过分割。
- 参数:
- 图像(M, N, C) ndarray
输入图像。可以通过 channel_axis 参数指定对应颜色通道的轴。
- 比率float, 可选, 介于 0 和 1 之间
平衡色彩空间接近度和图像空间接近度。更高的值给予色彩空间更多的权重。
- kernel_sizefloat, 可选
用于平滑样本密度的高斯核宽度。数值越高意味着聚类越少。
- max_distfloat, 可选
数据距离的截止点。数值越高意味着聚类越少。
- 返回树bool, 可选
是否返回完整的分割层次树和距离。
- sigmafloat, 可选
高斯平滑作为预处理步骤的宽度。零表示不进行平滑处理。
- convert2labbool, 可选
是否应在分割前将输入转换为Lab色彩空间。为此,假设输入为RGB。
- rng : {
numpy.random.Generator, int}, 可选toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。 伪随机数生成器。默认情况下,使用 PCG64 生成器(参见
numpy.random.default_rng())。如果 rng 是整数,则用于为生成器设定种子。PRNG 用于打破平局,默认情况下使用 42 作为种子。
- channel_axisint, 可选
对应于颜色通道的 image 轴。默认为最后一个轴。
- 返回:
- segment_mask(M, N) ndarray
整数掩码,指示段落标签。
注释
作者建议在分割之前将图像转换为Lab色彩空间,尽管这并非严格必要。为此,图像必须以RGB格式提供。
参考文献
[1]快速移位和核方法用于模式搜索,Vedaldi, A. 和 Soatto, S. 欧洲计算机视觉会议,2008
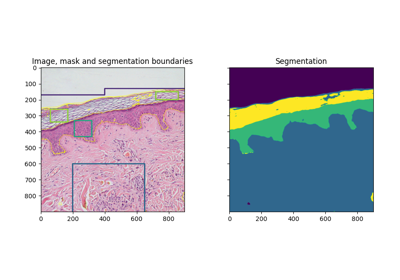
- skimage.segmentation.random_walker(data, labels, beta=130, mode='cg_j', tol=0.001, copy=True, return_full_prob=False, spacing=None, *, prob_tol=0.001, channel_axis=None)[源代码][源代码]#
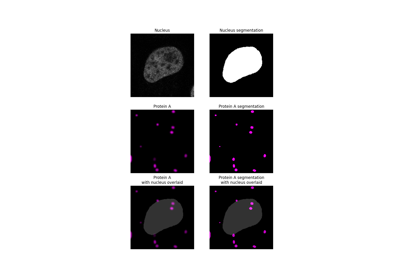
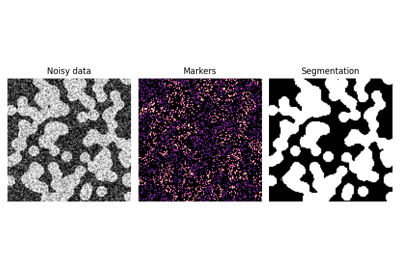
基于标记的分割随机游走算法。
随机游走算法是为灰度或多通道图像实现的。
- 参数:
- 数据(M, N[, P][, C]) ndarray
分阶段分割的图像。灰度 data 可以是二维或三维的;多通道数据可以是三维或四维的,其中 channel_axis 指定包含通道的维度。除非使用 spacing 关键字参数,否则数据间距假定为各向同性。
- 标签(M, N[, P]) 的整数数组
带有不同正整数的种子标记数组,用于区分不同阶段。零标记的像素是未标记的像素。负标签对应于不考虑的不活跃像素(它们从图中移除)。如果标签不是连续的整数,标签数组将被转换,使得标签是连续的。在多通道情况下,labels 应具有与 data 的单个通道相同的形状,即不包括表示通道的最终维度。
- betafloat, 可选
随机游走运动的惩罚系数(beta 越大,扩散越困难)。
- 模式字符串,可用选项 {‘cg’, ‘cg_j’, ‘cg_mg’, ‘bf’}
随机游走算法中求解线性系统的模式。
‘bf’ (暴力法): 计算拉普拉斯矩阵的LU分解。这对于小图像(<1024x1024)来说很快,但对于大图像(例如,3D体积)来说非常慢且内存密集。
‘cg’ (共轭梯度): 线性系统通过使用来自 scipy.sparse.linalg 的共轭梯度法迭代求解。对于大图像,这比暴力方法更节省内存,但速度较慢。
‘cg_j’(带Jacobi预处理器的共轭梯度法):在共轭梯度法迭代过程中应用Jacobi预处理器。这可能会加速’cg’方法的收敛。
‘cg_mg’(带多重网格预处理器的共轭梯度法):使用多重网格求解器计算预处理矩阵,然后使用共轭梯度法计算解。此模式要求安装了pyamg模块。
- tolfloat, 可选
使用基于共轭梯度的模式(’cg’、’cg_j’ 和 ‘cg_mg’)求解线性系统时,要达到的容差。
- 复制bool, 可选
如果 copy 为 False,labels 数组将被分段结果覆盖。如果你想节省内存,请使用 copy=False。
- return_full_probbool, 可选
如果为真,将返回每个像素属于每个标签的概率,而不仅仅是可能性最大的标签。
- 间距浮点数的可迭代对象,可选
每个空间维度中体素之间的间距。如果为 None,则假定每个维度中像素/体素之间的间距为 1。
- prob_tolfloat, 可选
结果概率在区间 [0, 1] 内的容差。如果容差不满足,则会显示警告。
- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19:
channel_axis在 0.19 版本中被添加。
- 返回:
- 输出ndarray
如果 return_full_prob 为 False,则返回一个与 labels 形状和数据类型相同的整数数组,其中每个像素根据最先通过各向异性扩散到达该像素的标记进行标记。
如果 return_full_prob 为 True,返回形状为 (nlabels, labels.shape) 的浮点数数组。output[label_nb, i, j] 是标签 label_nb 首先到达像素 (i, j) 的概率。
参见
skimage.segmentation.watershed一种基于数学形态学和从标记点开始的区域“泛洪”的分段算法。
注释
多通道输入会根据所有通道数据的总和进行缩放。在运行此算法之前,请确保所有通道都已单独归一化。
spacing 参数专门用于各向异性数据集,其中数据点在一个或多个空间维度上的间距不同。各向异性数据在医学影像中很常见。
该算法首次在 [1] 中提出。
该算法解决了在无限时间内,将源放置在每个相位的标记上依次进行扩散方程的问题。一个像素被标记为具有最大概率首先扩散到该像素的相位。
扩散方程通过最小化 x.T L x 来求解每个相位,其中 L 是图像加权图的拉普拉斯算子,x 是通过扩散到达像素的给定相位标记的概率(在相位标记上 x=1,在其他标记上 x=0,其他系数需要查找)。每个像素被赋予其具有最大 x 值的标签。图像的拉普拉斯算子 L 定义为:
L_ii = d_i, 像素 i 的邻居数量(i 的度)
L_ij = -w_ij 如果 i 和 j 是相邻像素
权重 w_ij 是局部梯度范数的递减函数。这确保了相似值的像素之间更容易发生扩散。
当拉普拉斯算子被分解为标记像素和未标记像素的块时:
L = M B.T B A
首先对应标记的像素,然后对应未标记的像素,最小化 x.T L x 对于一个相位相当于求解:
A x = - B x_m
其中 x_m 在给定相位的标记上为 1,在其他标记上为 0。该线性系统在算法中使用直接法求解小图像,使用迭代法求解大图像。
参考文献
[1]Leo Grady, 随机游走用于图像分割, IEEE Trans Pattern Anal Mach Intell. 2006年11月;28(11):1768-83. DOI:10.1109/TPAMI.2006.233.
示例
>>> rng = np.random.default_rng() >>> a = np.zeros((10, 10)) + 0.2 * rng.random((10, 10)) >>> a[5:8, 5:8] += 1 >>> b = np.zeros_like(a, dtype=np.int32) >>> b[3, 3] = 1 # Marker for first phase >>> b[6, 6] = 2 # Marker for second phase >>> random_walker(a, b) array([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 2, 2, 2, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]], dtype=int32)
- skimage.segmentation.relabel_sequential(label_field, offset=1)[源代码][源代码]#
将任意标签重新标记为 {offset, … offset + number_of_labels}。
此函数还返回正向映射(将原始标签映射到简化标签)和反向映射(将简化标签映射回原始标签)。
- 参数:
- label_fieldint 类型的 numpy 数组,任意形状
一组标签,必须是非负整数。
- 偏移量int, 可选
返回标签将从 offset 开始,该值应严格为正。
- 返回:
- 重新标记 : 整数类型的 numpy 数组,形状与 label_field 相同int 类型的 numpy 数组,形状相同
输入标签字段,标签映射到 {offset, …, number_of_labels + offset - 1}。数据类型将与 label_field 相同,除非 offset + number_of_labels 导致当前数据类型溢出。
- forward_map数组映射
从原始标签空间到返回标签空间的映射。可用于重新应用相同的映射。查看示例以了解用法。输出数据类型将与 relabeled 相同。
- inverse_map数组映射
从新标签空间到原始空间的映射。这可以用于从重新标记的字段重建原始标签字段。输出数据类型将与 label_field 相同。
注释
标签 0 被假定为表示背景,并且永远不会被重新映射。
对于某些输入,前向映射可能会非常大,因为其长度由标签字段的最大值给出。然而,在大多数情况下,
label_field.max()远小于label_field.size,在这些情况下,前向映射的大小保证小于输入或输出图像。示例
>>> from skimage.segmentation import relabel_sequential >>> label_field = np.array([1, 1, 5, 5, 8, 99, 42]) >>> relab, fw, inv = relabel_sequential(label_field) >>> relab array([1, 1, 2, 2, 3, 5, 4]) >>> print(fw) ArrayMap: 1 → 1 5 → 2 8 → 3 42 → 4 99 → 5 >>> np.array(fw) array([0, 1, 0, 0, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5]) >>> np.array(inv) array([ 0, 1, 5, 8, 42, 99]) >>> (fw[label_field] == relab).all() True >>> (inv[relab] == label_field).all() True >>> relab, fw, inv = relabel_sequential(label_field, offset=5) >>> relab array([5, 5, 6, 6, 7, 9, 8])
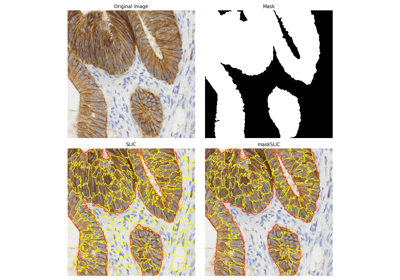
- skimage.segmentation.slic(image, n_segments=100, compactness=10.0, max_num_iter=10, sigma=0, spacing=None, convert2lab=None, enforce_connectivity=True, min_size_factor=0.5, max_size_factor=3, slic_zero=False, start_label=1, mask=None, *, channel_axis=-1)[源代码][源代码]#
使用颜色-(x,y,z)空间中的k-means聚类对图像进行分割。
- 参数:
- 图像(M, N[, P][, C]) ndarray
输入图像。可以是二维或三维,灰度或彩色(见 channel_axis 参数)。输入图像必须是无 NaN 的,或者 NaN 必须被遮罩掉。
- n_segmentsint, 可选
分割输出图像中的(近似)标签数量。
- 紧凑性float, 可选
平衡颜色接近度和空间接近度。较高的值给予空间接近度更多的权重,使得超像素形状更接近方形/立方形。在SLICO模式下,这是初始的紧凑度。此参数强烈依赖于图像对比度以及图像中物体的形状。我们建议在探索可能的值时使用对数刻度,例如0.01、0.1、1、10、100,然后在选定的值附近进行细化。
- max_num_iterint, 可选
k-means 的最大迭代次数。
- sigma浮点数或浮点数数组,可选
高斯平滑核的宽度,用于图像每个维度的预处理。如果是标量值,则相同的sigma值应用于每个维度。零表示不进行平滑处理。请注意,如果sigma是标量且提供了手动体素间距(参见注释部分),则`sigma`会自动缩放。如果sigma是类似数组的形式,其大小必须与``image``的空间维度数量匹配。
- 间距类似数组的浮点数,可选
每个空间维度的体素间距。默认情况下,
slic假设均匀间距(每个空间维度的体素分辨率相同)。此参数控制 k-means 聚类期间沿空间维度的距离权重。- convert2labbool, 可选
是否应在分割前将输入转换为Lab色彩空间。输入图像*必须*为RGB格式。强烈推荐。当
channel_axis不为 None 且image.shape[-1] == 3时,此选项默认设置为True。- enforce_connectivitybool, 可选
生成的段落是否连接
- min_size_factorfloat, 可选
相对于假设的段大小
`depth*width*height/n_segments`,要移除的最小段大小的比例- max_size_factorfloat, 可选
最大连接段大小的比例。值为3在大多数情况下有效。
- slic_zerobool, 可选
运行 SLIC-zero,这是 SLIC 的零参数模式。 [2]
- start_labelint, 可选
标签的索引起始。应为 0 或 1。
Added in version 0.17:
start_label在 0.17 版本中引入- 掩码ndarray,可选
如果提供了掩码,超像素仅在掩码为 True 的地方计算,并且种子点使用 k-means 聚类策略均匀分布在掩码上。掩码的维度数必须等于图像的空间维度数。
Added in version 0.17:
mask在 0.17 版本中引入- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19:
channel_axis在 0.19 版本中被添加。
- 返回:
- 标签2D 或 3D 数组
整数掩码,指示段落标签。
- Raises:
- ValueError
如果
convert2lab设置为True但最后一个数组维度长度不是3。- ValueError
如果
start_label不是 0 或 1。- ValueError
如果
image包含未屏蔽的 NaN 值。- ValueError
如果
image包含未屏蔽的无限值。- ValueError
如果
image是二维的,但channel_axis是 -1(默认值)。
注释
如果 sigma > 0,图像在分割前会使用高斯核进行平滑处理。
如果 sigma 是标量且提供了 spacing,核宽度将沿着每个维度被间距分割。例如,如果
sigma=1且spacing=[5, 1, 1],则有效的 sigma 是[0.2, 1, 1]。这确保了对各向异性图像的合理平滑。图像在处理前被重新缩放到 [0, 1] 范围内(忽略掩码值)。
形状为 (M, N, 3) 的图像默认被解释为 2D RGB 图像。要将其解释为 3D 图像,且最后一个维度长度为 3,请使用 channel_axis=None。
start_label 被引入以处理问题 [4]。标签索引默认从1开始。
参考文献
[1]Radhakrishna Achanta, Appu Shaji, Kevin Smith, Aurelien Lucchi, Pascal Fua, 和 Sabine Süsstrunk, SLIC 超像素与最先进的超像素方法比较, TPAMI, 2012年5月. DOI:10.1109/TPAMI.2012.120
[3]欧文, 本杰明. “maskSLIC: 区域超像素生成及其在医学图像局部病理特征化中的应用.”, 2016, arXiv:1606.09518
示例
>>> from skimage.segmentation import slic >>> from skimage.data import astronaut >>> img = astronaut() >>> segments = slic(img, n_segments=100, compactness=10)
增加紧凑度参数会产生更多方形区域:
>>> segments = slic(img, n_segments=100, compactness=20)
- skimage.segmentation.watershed(image, markers=None, connectivity=1, offset=None, mask=None, compactness=0, watershed_line=False)[源代码][源代码]#
在从给定标记淹没的图像中找到分水岭盆地。
- 参数:
- 图像(M, N[, …]) ndarray
数据数组,其中最低值的点首先被标记。
- 标记int,或 (M, N[, …]) 的 int 类型的 ndarray,可选
所需的盆地数量,或一个数组标记盆地,并在标签矩阵中分配值。零表示不是标记。如果为 None,则(默认)标记被确定为 image 的局部最小值。具体来说,计算等同于将
skimage.morphology.local_minima()应用于 image,然后对结果应用skimage.measure.label`(使用相同的给定 `connectivity())。一般来说,鼓励用户明确传递标记。- 连接性int 或 ndarray,可选
邻域连通性。整数被解释为
scipy.ndimage.generate_binary_structure中的最大正交步数,以到达邻居。数组直接被解释为足迹(结构元素)。默认值为1。在2D中,1给出4邻域,而2给出8邻域。- 偏移量类似数组的形状 image.ndim,可选
足迹中心的坐标。
- 掩码(M, N[, …]) 布尔值或0和1的ndarray,可选
与 image 形状相同的数组。只有当 mask == True 时的点才会被标记。
- 紧凑性float, 可选
使用紧凑分水岭 [1] 并给定紧凑性参数。较高的值会导致形状更规则的分水岭盆地。
- 分水岭线bool, 可选
如果为真,一条一像素宽的线将分水岭算法得到的区域分开。这条线标签为0。请注意,用于添加这条线的方法期望标记区域不相邻;分水岭线可能无法捕捉相邻标记区域之间的边界。
- 返回:
- 出ndarray
一个与 markers 类型和形状相同的标记矩阵。
参见
skimage.segmentation.random_walker基于各向异性扩散的分割算法,通常比分水岭算法慢,但在处理噪声数据和带有孔洞的边界时效果良好。
注释
此函数实现了一个分水岭算法 [2] [3] ,该算法将像素分配到标记的流域中。该算法使用优先队列来保存像素,优先队列的度量标准是像素值,然后是进入队列的时间——这解决了优先级相同的像素中,距离标记最近的像素优先的问题。
一些想法来自 [4]。论文中最重要的一点是,进入队列的时间解决了两个问题:一个像素应该被分配给具有最大梯度的邻居,或者如果没有梯度,平坦区域上的像素应该在相对两侧的标记之间进行分割。
此实现将所有参数转换为特定的、最低公分母类型,然后将这些参数传递给C算法。
标记可以手动确定,或者通过自动方式确定,例如使用图像梯度的局部最小值,或用于分离重叠对象的到背景距离函数的局部最大值(参见示例)。
参考文献
[1]P. Neubert and P. Protzel, “Compact Watershed and Preemptive SLIC: On Improving Trade-offs of Superpixel Segmentation Algorithms,” 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 2014, pp. 996-1001, DOI:10.1109/ICPR.2014.181 https://www.tu-chemnitz.de/etit/proaut/publications/cws_pSLIC_ICPR.pdf
[2]https://en.wikipedia.org/wiki/Watershed_%28图像处理%29
[4]P. J. Soille and M. M. Ansoult, “Automated basin delineation from digital elevation models using mathematical morphology,” Signal Processing, 20(2):171-182, DOI:10.1016/0165-1684(90)90127-K
示例
分水岭算法对于分离重叠物体非常有用。
我们首先生成一个包含两个重叠圆的初始图像:
>>> x, y = np.indices((80, 80)) >>> x1, y1, x2, y2 = 28, 28, 44, 52 >>> r1, r2 = 16, 20 >>> mask_circle1 = (x - x1)**2 + (y - y1)**2 < r1**2 >>> mask_circle2 = (x - x2)**2 + (y - y2)**2 < r2**2 >>> image = np.logical_or(mask_circle1, mask_circle2)
接下来,我们希望分离这两个圆。我们在距离背景的最大值处生成标记:
>>> from scipy import ndimage as ndi >>> distance = ndi.distance_transform_edt(image) >>> from skimage.feature import peak_local_max >>> max_coords = peak_local_max(distance, labels=image, ... footprint=np.ones((3, 3))) >>> local_maxima = np.zeros_like(image, dtype=bool) >>> local_maxima[tuple(max_coords.T)] = True >>> markers = ndi.label(local_maxima)[0]
最后,我们在图像和标记上运行分水岭算法:
>>> labels = watershed(-distance, markers, mask=image)
该算法同样适用于3D图像,例如可以用于分离重叠的球体。