skimage.morphology#
用于操作图像中形状的工具。
这些操作特别适合二值图像,尽管其中一些也可能对其他类型的图像有用。
基本的形态学操作包括膨胀和腐蚀。
对图像执行区域闭合操作。 |
|
对图像执行区域开运算。 |
|
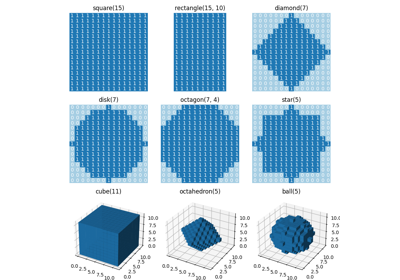
生成一个球形的足迹。 |
|
返回图像的快速二进制形态闭合。 |
|
返回图像的快速二值形态学膨胀。 |
|
返回图像的快速二值形态学腐蚀。 |
|
返回图像的快速二值形态学开运算。 |
|
返回图像的黑色顶帽。 |
|
返回图像的灰度形态学闭合。 |
|
计算二值图像的凸包图像。 |
|
计算二值图像中各个对象的凸包图像。 |
|
生成一个立方体形状的足迹。 |
|
对图像执行直径闭合操作。 |
|
对图像执行直径开运算。 |
|
生成一个扁平的菱形足迹。 |
|
返回图像的灰度形态学膨胀。 |
|
生成一个扁平的、圆盘状的足迹。 |
|
生成一个扁平的、椭圆形的足迹。 |
|
返回图像的灰度形态学腐蚀。 |
|
对应于泛洪填充的掩码。 |
|
对图像执行填充操作。 |
|
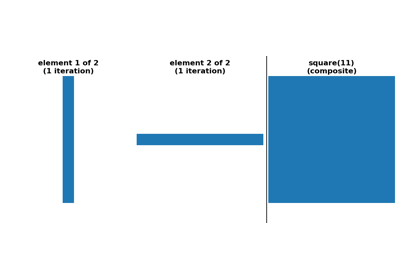
将一个足迹序列转换为等效的 ndarray。 |
|
确定图像中所有高度 >= h 的极大值。 |
|
确定图像中深度 >= h 的所有最小值。 |
|
返回图像的二值形态学闭合。 |
|
返回图像的二值形态膨胀。 |
|
返回图像的二值形态学腐蚀。 |
|
返回图像的二进制形态学开运算。 |
|
标记整数数组的连通区域。 |
|
查找 n 维数组的局部最大值。 |
|
查找 n 维数组的局部最小值。 |
|
从图像中构建最大树。 |
|
确定图像的所有局部最大值。 |
|
计算二值图像的中轴变换。 |
|
在足迹中镜像每个维度。 |
|
生成一个八边形形状的焊盘。 |
|
生成一个八面体形状的足迹。 |
|
返回图像的灰度形态学开运算。 |
|
将每个维度上的足迹填充为奇数大小。 |
|
对图像进行形态学重建。 |
|
生成一个平坦的矩形形状的焊盘。 |
|
按指定顺序移除对象,直到剩余对象之间的距离达到最小。 |
|
移除小于指定尺寸的连续孔洞。 |
|
移除小于指定尺寸的对象。 |
|
计算二值图像的骨架。 |
|
生成一个扁平的、方形的外形。 |
|
生成一个星形焊盘。 |
|
对二值图像进行形态学细化。 |
|
返回图像的白色顶帽。 |
- skimage.morphology.area_closing(image, area_threshold=64, connectivity=1, parent=None, tree_traverser=None)[源代码][源代码]#
对图像执行区域闭合操作。
区域闭合移除图像中所有表面积小于 area_threshold 的暗结构。输出图像在每个像素上大于或等于输入图像,并且所有局部最小值至少具有 area_threshold 像素的表面积。
区域闭合类似于形态学闭合,但它们不使用固定的结构元素,而是使用可变形的结构元素,其表面 = area_threshold。
在二值情况下,区域闭合等价于去除小孔;因此,此操作符被扩展到灰度图像。
从技术上讲,此操作符基于图像的最大树表示。
- 参数:
- 图像ndarray
要计算 area_closing 的输入图像。该图像可以是任何类型。
- area_threshold无符号整数
尺寸参数(像素数)。默认值任意选择为64。
- 连接性无符号整数,可选
邻域连通性。整数表示到达邻居所需的最大正交步数。在2D中,4邻域为1,8邻域为2。默认值为1。
- 父级ndarray, int64, 可选
表示反向图像的最大树的父图像。每个像素的值是其父节点在展平数组中的索引。详情请参见注释。
- tree_traverser1D 数组, int64, 可选
有序的像素索引(指向展平数组)。像素的排序方式是每个像素都紧随其父像素之后(根像素除外,因为它没有父像素)。
- 返回:
- 输出ndarray
输出图像与输入图像具有相同的形状和类型。
参见
注释
如果给函数提供了最大树表示(父节点和树遍历器),它们必须从图像的反转计算得出,即: >>> P, S = max_tree(invert(f)) >>> closed = diameter_closing(f, 3, parent=P, tree_traverser=S)
参考文献
[1]Vincent L., Proc. “灰度区域开闭运算,其高效实现及应用”, EURASIP 数学形态学及其在信号处理中的应用研讨会, 巴塞罗那, 西班牙, 第22-27页, 1993年5月。
[2]Soille, P., “形态图像分析:原理与应用” (第6章), 第二版 (2003), ISBN 3540429883. DOI:10.1007/978-3-662-05088-0
[3]Salembier, P., Oliveras, A., & Garrido, L. (1998). 反扩展连通算子用于图像和序列处理。IEEE图像处理汇刊, 7(4), 555-570. DOI:10.1109/83.663500
[4]Najman, L., & Couprie, M. (2006). 构建准线性时间内的组件树。IEEE图像处理汇刊, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[5]Carlinet, E., & Geraud, T. (2014). 组件树计算算法比较综述. IEEE图像处理汇刊, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
示例
我们创建一个图像(中心有一个最小值的二次函数和4个额外的局部最小值。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 180 + 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 160; f[2:4,9:11] = 140; f[9:11,2:4] = 120 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
我们可以计算区域闭合:
>>> closed = area_closing(f, 8, connectivity=1)
所有小的极小值都被移除,剩余的极小值至少有8的大小。
- skimage.morphology.area_opening(image, area_threshold=64, connectivity=1, parent=None, tree_traverser=None)[源代码][源代码]#
对图像执行区域开运算。
区域开启移除图像中所有表面积小于 area_threshold 的明亮结构。因此,输出图像是所有局部最大值至少具有 area_threshold 像素表面积的最大图像,小于输入图像。
区域开运算类似于形态学开运算,但它们不使用固定的结构元素,而是使用一个可变形的结构元素,其面积等于 area_threshold。因此,当 area_threshold=1 时,区域开运算就是恒等运算。
在二值情况下,区域开运算等价于移除小对象;因此,该操作符被扩展到灰度图像。
从技术上讲,此操作符基于图像的最大树表示。
- 参数:
- 图像ndarray
要计算区域开运算的输入图像。该图像可以是任何类型。
- area_threshold无符号整数
尺寸参数(像素数)。默认值任意选择为64。
- 连接性无符号整数,可选
邻域连通性。整数表示到达邻居所需的最大正交步数。在2D中,4邻域为1,8邻域为2。默认值为1。
- 父级ndarray, int64, 可选
表示图像最大树的父图像。每个像素的值是其父节点在展平数组中的索引。
- tree_traverser1D 数组, int64, 可选
有序的像素索引(指向展平数组)。像素的排序方式是每个像素都紧随其父像素之后(根像素除外,因为它没有父像素)。
- 返回:
- 输出ndarray
输出图像与输入图像具有相同的形状和类型。
参见
参考文献
[1]Vincent L., Proc. “灰度区域开闭运算,其高效实现及应用”, EURASIP 数学形态学及其在信号处理中的应用研讨会, 巴塞罗那, 西班牙, 第22-27页, 1993年5月。
[2]Soille, P., “形态图像分析:原理与应用” (第6章), 第二版 (2003), ISBN 3540429883. DOI:10.1007/978-3-662-05088-0
[3]Salembier, P., Oliveras, A., & Garrido, L. (1998). 反扩展连通算子用于图像和序列处理。IEEE图像处理汇刊, 7(4), 555-570. DOI:10.1109/83.663500
[4]Najman, L., & Couprie, M. (2006). 构建准线性时间内的组件树。IEEE图像处理汇刊, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[5]Carlinet, E., & Geraud, T. (2014). 组件树计算算法比较综述. IEEE图像处理汇刊, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
示例
我们创建一个图像(中心有一个最大值的二次函数,以及4个额外的局部最大值。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 40; f[2:4,9:11] = 60; f[9:11,2:4] = 80 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
我们可以计算开口面积:
>>> open = area_opening(f, 8, connectivity=1)
表面积小于8的峰被移除。
- skimage.morphology.ball(radius, dtype=<class 'numpy.uint8'>, *, strict_radius=True, decomposition=None)[源代码][源代码]#
生成一个球形的足迹。
这是磁盘的3D等价物。如果一个像素与原点之间的欧几里得距离不大于半径,则该像素在邻域内。
- 参数:
- 半径整数
球形足迹的半径。
- 返回:
- 足迹ndarray 或 元组
邻域元素为1,其他地方为0的足迹。
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- strict_radiusbool, 可选
如果为 False,则将半径扩展 0.5。这允许圆在每个轴上保持大小为
2 * 半径 + 1的立方体内进一步扩展。如果分解不为 None,则忽略此参数。- 分解{None, ‘sequence’}, 可选
如果为 None,则返回一个单独的数组。对于 ‘sequence’,返回一个较小足迹的元组。应用这一系列较小的足迹将得到与单个较大足迹相当的结果,但具有更好的计算性能。对于球形足迹,序列分解并不完全等同于分解=None。更多详情请参见注释。
注释
通过 decomposition=’sequence’ 模式生成的磁盘与 decomposition=None 生成的磁盘并不相同。这里我们将 [1] 中对磁盘的方法扩展到三维情况,使用了该出版物中“方形”、“菱形”和“T形”元素的三维扩展。所有这些基本元素的大小均为
(3,) * ndim。我们通过数值计算了每个元素的重复次数,以最接近于使用 kwargsstrict_radius=False, decomposition=None计算的球体。从经验上看,序列分解方法的等效复合足迹接近于一个菱形立方八面体(26个面 [2])。
参考文献
[1]Park, H 和 Chin R.T. 结构元素的分解以实现形态学操作的最佳实现。在 Proceedings: 1997 IEEE 非线性信号与图像处理研讨会, 伦敦, 英国。https://www.iwaenc.org/proceedings/1997/nsip97/pdf/scan/ns970226.pdf
- skimage.morphology.binary_closing(image, footprint=None, out=None, *, mode='ignore')[源代码][源代码]#
返回图像的快速二进制形态闭合。
此函数返回与灰度闭合相同的结果,但对于二值图像执行速度更快。
图像的形态学闭运算是指先进行膨胀操作,然后进行腐蚀操作。闭运算可以去除小的暗点(即“胡椒”)并连接小的亮裂缝。这往往会“闭合”(暗)特征之间的(亮)间隙。
- 参数:
- 图像ndarray
二进制输入图像。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递了 None,将分配一个新的数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式有:’max’, ‘min’, ‘ignore’。如果为 ‘ignore’,图像域外的像素在腐蚀时被假设为 True,在膨胀时被假设为 False,这使得它们不会影响结果。默认值是 ‘ignore’。
Added in version 0.23: mode 在 0.23 版本中被添加。
- 返回:
- 关闭布尔类型的 ndarray
形态学闭运算的结果。
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。
- skimage.morphology.binary_dilation(image, footprint=None, out=None, *, mode='ignore')[源代码][源代码]#
返回图像的快速二值形态学膨胀。
此函数返回与灰度膨胀相同的结果,但对于二值图像执行速度更快。
形态学膨胀将像素
(i,j)设置为以(i,j)为中心的邻域内所有像素的最大值。膨胀会扩大亮区并缩小暗区。- 参数:
- 图像ndarray
二进制输入图像。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式有:’max’, ‘min’, ‘ignore’。如果使用 ‘min’ 或 ‘ignore’,图像域外的像素被假定为 False,这使得它们不会影响结果。默认是 ‘ignore’。
Added in version 0.23: mode 在 0.23 版本中被添加。
- 返回:
- 扩张的bool 或 uint 的 ndarray
形态学膨胀的结果,值在
[False, True]中。
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。对于非对称结构元素,
skimage.morphology.binary_dilation()和skimage.morphology.dilation()产生的输出有所不同:binary_dilation会镜像结构元素,而dilation则不会。
- skimage.morphology.binary_erosion(image, footprint=None, out=None, *, mode='ignore')[源代码][源代码]#
返回图像的快速二值形态学腐蚀。
此函数返回与灰度腐蚀相同的结果,但对于二值图像执行速度更快。
形态学腐蚀将像素
(i,j)设置为以(i,j)为中心的邻域内所有像素的最小值。腐蚀会缩小亮区域并扩大暗区域。- 参数:
- 图像ndarray
二进制输入图像。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效模式包括:’max’、’min’、’ignore’。如果为 ‘max’ 或 ‘ignore’,图像域外的像素被假定为 True,这导致它们不影响结果。默认值是 ‘ignore’。
Added in version 0.23: mode 在 0.23 版本中被添加。
- 返回:
- 侵蚀bool 或 uint 的 ndarray
形态学腐蚀的结果,取值在
[False, True]中。
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。对于偶数大小的结构元素,
skimage.morphology.erosion()和此函数生成的输出会有所不同:一个相对于另一个偏移了一个像素。
- skimage.morphology.binary_opening(image, footprint=None, out=None, *, mode='ignore')[源代码][源代码]#
返回图像的快速二值形态学开运算。
此函数返回与灰度开运算相同的结果,但对于二值图像执行速度更快。
图像上的形态学开运算是指先腐蚀后膨胀的操作。开运算可以去除小的亮点(即“盐”)并连接小的暗裂缝。这往往会“打开”(暗)特征之间的(亮)间隙。
- 参数:
- 图像ndarray
二进制输入图像。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式有:’max’, ‘min’, ‘ignore’。如果为 ‘ignore’,图像域外的像素在腐蚀时被假设为 True,在膨胀时被假设为 False,这使得它们不会影响结果。默认值是 ‘ignore’。
Added in version 0.23: mode 在 0.23 版本中被添加。
- 返回:
- 开幕布尔类型的 ndarray
形态学开运算的结果。
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。
- skimage.morphology.black_tophat(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[源代码][源代码]#
返回图像的黑色顶帽。
图像的黑色礼帽被定义为其形态学闭运算减去原始图像。此操作返回图像中比结构元素小的暗斑。注意,原始图像中的暗斑在黑色礼帽操作后变为亮斑。
- 参数:
- 图像ndarray
图像数组。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式包括:’reflect’、’constant’、’nearest’、’mirror’、’wrap’、’max’、’min’ 或 ‘ignore’。参见
skimage.morphology.closing()。默认值为 ‘reflect’。- cval标量,可选
如果 mode 是 ‘constant’,则用于填充输入边缘之外的值。默认值为 0.0。
Added in version 0.23: mode 和 cval 在 0.23 版本中被添加。
- 返回:
- out : 数组, 与 image 形状和类型相同数组,形状和类型与
形态学黑帽运算的结果。
参见
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。参考文献
示例
>>> # Change dark peak to bright peak and subtract background >>> import numpy as np >>> from skimage.morphology import square >>> dark_on_gray = np.array([[7, 6, 6, 6, 7], ... [6, 5, 4, 5, 6], ... [6, 4, 0, 4, 6], ... [6, 5, 4, 5, 6], ... [7, 6, 6, 6, 7]], dtype=np.uint8) >>> black_tophat(dark_on_gray, square(3)) array([[0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 1, 5, 1, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.closing(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[源代码][源代码]#
返回图像的灰度形态学闭合。
图像的形态学闭合操作定义为先膨胀后腐蚀。闭合操作可以去除小的暗斑(即“胡椒”)并连接小的亮裂缝。这通常会“闭合”(暗)特征之间的(亮)间隙。
- 参数:
- 图像ndarray
图像数组。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出ndarray,可选
用于存储形态学结果的数组。如果为 None,将分配一个新的数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式包括:’reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’, ‘max’, ‘min’, 或 ‘ignore’。如果选择 ‘ignore’,图像域外的像素被假设为图像数据类型的最大值用于腐蚀操作,最小值用于膨胀操作,这使得它们不会影响结果。默认值是 ‘reflect’。
- cval标量,可选
如果 mode 是 ‘constant’,则用于填充输入边缘之外的值。默认值为 0.0。
Added in version 0.23: mode 和 cval 在 0.23 版本中被添加。
- 返回:
- closing : 数组,形状和类型与 image 相同数组,形状和类型与
形态学闭运算的结果。
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。示例
>>> # Close a gap between two bright lines >>> import numpy as np >>> from skimage.morphology import square >>> broken_line = np.array([[0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0], ... [1, 1, 0, 1, 1], ... [0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0]], dtype=np.uint8) >>> closing(broken_line, square(3)) array([[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [1, 1, 1, 1, 1], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)
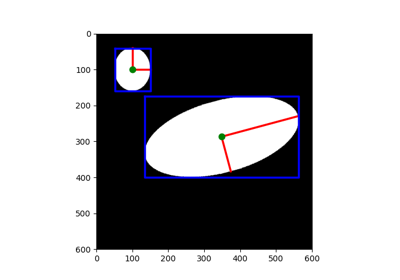
- skimage.morphology.convex_hull_image(image, offset_coordinates=True, tolerance=1e-10, include_borders=True)[源代码][源代码]#
计算二值图像的凸包图像。
凸包是包含输入图像中所有白色像素的最小凸多边形所包含的像素集合。
- 参数:
- 图像数组
二进制输入图像。此数组在处理前会被转换为布尔类型。
- 偏移坐标bool, 可选
如果
True,坐标上的一个像素,例如 (4, 7) ,将由坐标 (3.5, 7), (4.5, 7), (4, 6.5) 和 (4, 7.5) 表示。这在计算凸包时为像素增加了一些“范围”。- 容差float, 可选
确定一个点是否在凸包内时的容差。由于数值浮点误差,容差为0可能导致某些点被错误地分类为在凸包外。
- include_borders: bool, 可选
如果
False,顶点/边将被排除在最终的凸包掩码之外。
- 返回:
- 船体(M, N) 布尔数组
二值图像,凸包内的像素设置为 True。
参考文献
- skimage.morphology.convex_hull_object(image, *, connectivity=2)[源代码][源代码]#
计算二值图像中各个对象的凸包图像。
凸包是包含输入图像中所有白色像素的最小凸多边形所包含的像素集合。
- 参数:
- 图像(M, N) ndarray
二进制输入图像。
- 连接性{1, 2}, int, 可选
确定每个像素的邻域。在像素中心方距离
connectivity内的相邻元素被视为邻域。:1-connectivity 2-connectivity [ ] [ ] [ ] [ ] | \ | / [ ]--[x]--[ ] [ ]--[x]--[ ] | / | \ [ ] [ ] [ ] [ ]
- 返回:
- 船体布尔类型的 ndarray
二值图像,凸包内的像素设置为
True。
注释
此函数使用
skimage.morphology.label来定义唯一对象,使用convex_hull_image找到每个对象的凸包,并使用逻辑或组合这些区域。请注意,未连接对象的凸包在结果中可能会重叠。如果怀疑这种情况,请考虑分别对每个对象使用 convex_hull_image 或调整connectivity。
- skimage.morphology.cube(width, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个立方体形状的足迹。
这是正方形的3D等价物。沿周长的每个像素的棋盘距离都不大于半径(半径=floor(宽度/2))像素。
- 参数:
- 宽度整数
立方体的宽度、高度和深度。
- 返回:
- 足迹ndarray 或 元组
邻域元素为1,其他地方为0的足迹。当 decomposition 为 None 时,这只是一个 numpy.ndarray。否则,这将是一个元组,其长度等于要应用的唯一结构元素的数量(详见注释)
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘separable’, ‘sequence’}, 可选
如果为 None,则返回一个数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但通常具有更好的计算性能。更多详情请参见注释。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。对于二值形态学,使用
decomposition='sequence'被观察到能提供更好的性能,性能提升的幅度随着足迹大小的增加而迅速增加。对于带有方形足迹的灰度形态学,建议使用decomposition=None,因为所调用的内部 SciPy 函数已经基于可分离的 1D 滑动窗口实现了快速实现。“序列”分解模式仅支持奇数值的 width。如果 width 是偶数,所使用的序列将与“可分离”模式相同。
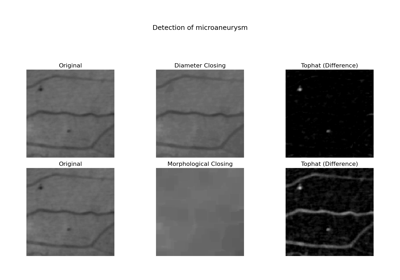
- skimage.morphology.diameter_closing(image, diameter_threshold=8, connectivity=1, parent=None, tree_traverser=None)[源代码][源代码]#
对图像执行直径闭合操作。
直径闭合移除图像中最大扩展小于直径阈值的所有暗结构。最大扩展定义为边界框的最大扩展。该操作符也称为边界框闭合。实际上,结果类似于形态学闭合,但长而细的结构不会被移除。
从技术上讲,此操作符基于图像的最大树表示。
- 参数:
- 图像ndarray
要计算直径闭合的输入图像。该图像可以是任何类型。
- 直径阈值无符号整数
最大扩展参数(像素数)。默认值为8。
- 连接性无符号整数,可选
邻域连通性。整数表示到达邻居所需的最大正交步数。在2D中,4邻域为1,8邻域为2。默认值为1。
- 父级ndarray, int64, 可选
预计算的父图像,表示反转图像的最大树。如果提供了预计算的父图像和tree_traverser,此函数速度很快。详见注释。
- tree_traverser1D 数组, int64, 可选
预计算的遍历器,其中像素按顺序排列,使得每个像素都在其父像素之后(根像素除外,它没有父像素)。如果提供了预计算的父像素和树遍历器,此函数速度很快。详见注释。
- 返回:
- 输出ndarray
输出图像与输入图像具有相同的形状和类型。
参见
注释
如果给函数提供了最大树表示(父节点和树遍历器),它们必须从图像的反转计算得出,即: >>> P, S = max_tree(invert(f)) >>> closed = diameter_closing(f, 3, parent=P, tree_traverser=S)
参考文献
[1]Walter, T., & Klein, J.-C. (2002). 使用边界框闭合方法在人眼底彩色图像中自动检测微动脉瘤。在 A. Colosimo, P. Sirabella, A. Giuliani (编), 医学数据分析. 计算机科学讲义, 第2526卷, 第210-220页. Springer Berlin Heidelberg. DOI:10.1007/3-540-36104-9_23
[2]Carlinet, E., & Geraud, T. (2014). 组件树计算算法比较综述. IEEE图像处理汇刊, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
示例
我们创建一个图像(中心有一个最小值的二次函数和4个额外的局部最小值。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 180 + 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 160; f[2:4,9:11] = 140; f[9:11,2:4] = 120 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
我们可以计算直径闭合:
>>> closed = diameter_closing(f, 3, connectivity=1)
所有最大扩展不超过2的小极小值都被移除。剩余的极小值的最大扩展至少为3。
- skimage.morphology.diameter_opening(image, diameter_threshold=8, connectivity=1, parent=None, tree_traverser=None)[源代码][源代码]#
对图像执行直径开运算。
直径开运算移除图像中最大扩展小于直径阈值的所有明亮结构。最大扩展定义为边界框的最大扩展。该操作符也称为边界框开运算。实际上,结果类似于形态学开运算,但长而细的结构不会被移除。
从技术上讲,此操作符基于图像的最大树表示。
- 参数:
- 图像ndarray
要计算区域开运算的输入图像。该图像可以是任何类型。
- 直径阈值无符号整数
最大扩展参数(像素数)。默认值为8。
- 连接性无符号整数,可选
邻域连通性。整数表示到达邻居所需的最大正交步数。在2D中,4邻域为1,8邻域为2。默认值为1。
- 父级ndarray, int64, 可选
表示图像最大树的父图像。每个像素的值是其父节点在展平数组中的索引。
- tree_traverser1D 数组, int64, 可选
有序的像素索引(指向展平数组)。像素的排序方式是每个像素都紧随其父像素之后(根像素除外,因为它没有父像素)。
- 返回:
- 输出ndarray
输出图像与输入图像具有相同的形状和类型。
参见
参考文献
[1]Walter, T., & Klein, J.-C. (2002). 使用边界框闭合方法在人眼底彩色图像中自动检测微动脉瘤。在 A. Colosimo, P. Sirabella, A. Giuliani (编), 医学数据分析. 计算机科学讲义, 第2526卷, 第210-220页. Springer Berlin Heidelberg. DOI:10.1007/3-540-36104-9_23
[2]Carlinet, E., & Geraud, T. (2014). 组件树计算算法比较综述. IEEE图像处理汇刊, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
示例
我们创建一个图像(中心有一个最大值的二次函数,以及4个额外的局部最大值。
>>> w = 12 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:3,1:5] = 40; f[2:4,9:11] = 60; f[9:11,2:4] = 80 >>> f[9:10,9:11] = 100; f[10,10] = 100 >>> f = f.astype(int)
我们可以计算直径开口:
>>> open = diameter_opening(f, 3, connectivity=1)
最大扩展度为2或更小的峰被移除。剩余的峰的最大扩展度都至少为3。
- skimage.morphology.diamond(radius, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个扁平的菱形足迹。
如果一个像素与邻域中心之间的城市街区/曼哈顿距离不大于半径,则该像素是邻域的一部分(即标记为1)。
- 参数:
- 半径整数
钻石形状的足迹的半径。
- 返回:
- 足迹ndarray 或 元组
邻域元素为1,其他地方为0的足迹。当 decomposition 为 None 时,这只是一个 numpy.ndarray。否则,这将是一个元组,其长度等于要应用的唯一结构元素的数量(详见注释)
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘sequence’}, 可选
如果为 None,则返回一个数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但具有更好的计算性能。更多详情请参见注释。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。无论是二值还是灰度形态学,使用
decomposition='sequence'都被观察到具有性能优势,且随着足迹大小的增加,这种优势的幅度也会增加。
- skimage.morphology.dilation(image, footprint=None, out=None, shift_x=<DEPRECATED>, shift_y=<DEPRECATED>, *, mode='reflect', cval=0.0)[源代码][源代码]#
返回图像的灰度形态学膨胀。
形态学膨胀将一个像素的值设置为以该像素为中心的局部邻域内所有像素值的最大值。足迹为1的值定义了这个邻域。膨胀扩大明亮区域并缩小暗区域。
- 参数:
- 图像ndarray
图像数组。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式包括:’reflect’、’constant’、’nearest’、’mirror’、’wrap’、’max’、’min’ 或 ‘ignore’。如果使用 ‘min’ 或 ‘ignore’,图像域外的像素被假设为图像数据类型的最大值,这使得它们不会影响结果。默认值是 ‘reflect’。
- cval标量,可选
如果 mode 是 ‘constant’,则用于填充输入边缘之外的值。默认值为 0.0。
Added in version 0.23: mode 和 cval 在 0.23 版本中被添加。
- 返回:
- dilated : uint8 数组, 与 image 形状和类型相同uint8 数组,形状和类型与
形态学膨胀的结果。
- 其他参数:
- shift_x, shift_y已弃用
自 0.23 版本弃用.
注释
对于
uint8``(以及在一定位深度下的 ``uint16)数据,较低的算法复杂度使得skimage.filters.rank.maximum()函数在处理较大图像和结构元素时更加高效。足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。对于非对称结构元素,
skimage.morphology.binary_dilation()和skimage.morphology.dilation()产生的输出有所不同:binary_dilation会镜像结构元素,而dilation则不会。示例
>>> # Dilation enlarges bright regions >>> import numpy as np >>> from skimage.morphology import square >>> bright_pixel = np.array([[0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0], ... [0, 0, 1, 0, 0], ... [0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0]], dtype=np.uint8) >>> dilation(bright_pixel, square(3)) array([[0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.disk(radius, dtype=<class 'numpy.uint8'>, *, strict_radius=True, decomposition=None)[源代码][源代码]#
生成一个扁平的、圆盘状的足迹。
如果一个像素与原点之间的欧几里得距离不大于半径,则该像素位于邻域内(当 decomposition == ‘sequence’ 时,这仅是近似正确)。
- 参数:
- 半径整数
圆盘形足迹的半径。
- 返回:
- 足迹ndarray
邻域元素为1,其他地方为0的足迹。
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- strict_radiusbool, 可选
如果为 False,则将半径扩展 0.5。这允许圆在每个轴上保持大小为
2 * 半径 + 1的立方体内进一步扩展。如果分解不为 None,则忽略此参数。- 分解{None, ‘sequence’, ‘crosses’}, 可选
如果为 None,则返回一个单独的数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相当的结果,但具有更好的计算性能。对于磁盘足迹,’sequence’ 或 ‘crosses’ 分解并不总是与
decomposition=None完全等效。更多详情请参见注释。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。通过
decomposition='sequence'模式生成的磁盘可能与decomposition=None生成的磁盘不完全相同。一个磁盘的足迹可以通过沿每个轴应用一系列范围为3的小足迹来近似。对于半径为2到10的二维磁盘,具体的解决方案在 [1] 中给出。在这里,我们通过数值计算了每个元素的重复次数,这些元素给出了与使用 kwargsstrict_radius=False, decomposition=None计算的磁盘最接近的匹配。经验上,在大半径处的系列分解接近一个十六边形(一个16边的多边形 [2])。在 [3] 中,作者们证明了十六边形是使用形状为 (3, 3) 的足迹进行分解时,最接近圆盘的近似。
使用
decomposition='crosses'生成的磁盘通常但不总是与decomposition=None生成的磁盘相同。它往往比decomposition='sequence'提供更接近的近似值,性能相当可比。单独的十字形元素的大小不受 (3, 3) 的限制。与 ‘sequence’ 分解不同,’crosses’ 分解还可以准确地近似形状为strict_radius=True的磁盘。该方法基于 [4] 中给出的算法 1 的改编。参考文献
[1]Park, H 和 Chin R.T. 结构元素的分解以实现形态学操作的最佳实现。在 Proceedings: 1997 IEEE 非线性信号与图像处理研讨会, 伦敦, 英国。https://www.iwaenc.org/proceedings/1997/nsip97/pdf/scan/ns970226.pdf
[3]Vanrell, M 和 Vitrià, J. 形态变换的最优 3 × 3 可分解盘。《图像与视觉计算》,第 15 卷,第 11 期,1997 年。DOI:10.1016/S0262-8856(97)00026-7
[4]Li, D. 和 Ritter, G.X. 可分离和对称凸模板的分解。Proc. SPIE 1350, 图像代数和形态图像处理, (1990年11月1日). DOI:10.1117/12.23608
- skimage.morphology.ellipse(width, height, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个扁平的、椭圆形的足迹。
椭圆周长上的每一个像素都满足方程
(x/width+1)**2 + (y/height+1)**2 = 1。- 参数:
- 宽度整数
椭圆形足迹的宽度。
- 高度整数
椭圆形足迹的高度。
- 返回:
- 足迹ndarray
邻域元素为1,其他地方为0的足迹。足迹的形状将是
(2 * 高度 + 1, 2 * 宽度 + 1)。
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘crosses’}, 可选
如果为 None,则返回一个数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但具有更好的计算性能。更多详情请参见注释。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。由
decomposition='crosses'产生的椭圆通常但并不总是与decomposition=None产生的椭圆相同。该方法基于 [1] 中给出的算法 1 的改编。参考文献
[1]Li, D. 和 Ritter, G.X. 可分离和对称凸模板的分解。Proc. SPIE 1350, 图像代数和形态图像处理, (1990年11月1日). DOI:10.1117/12.23608
示例
>>> from skimage.morphology import footprints >>> footprints.ellipse(5, 3) array([[0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0]], dtype=uint8)
- skimage.morphology.erosion(image, footprint=None, out=None, shift_x=<DEPRECATED>, shift_y=<DEPRECATED>, *, mode='reflect', cval=0.0)[源代码][源代码]#
返回图像的灰度形态学腐蚀。
形态学腐蚀将位于 (i,j) 的像素设置为以 (i,j) 为中心的邻域内所有像素的最小值。腐蚀会缩小亮区域并扩大暗区域。
- 参数:
- 图像ndarray
图像数组。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出ndarrays,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式有:’reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’, ‘max’, ‘min’, 或 ‘ignore’。如果选择 ‘max’ 或 ‘ignore’,图像域外的像素被假定为图像数据类型的最大值,这使得它们不会影响结果。默认值是 ‘reflect’。
- cval标量,可选
如果 mode 是 ‘constant’,则用于填充输入边缘之外的值。默认值为 0.0。
Added in version 0.23: mode 和 cval 在 0.23 版本中被添加。
- 返回:
- eroded : 数组,形状与 image 相同数组,形状相同
形态学腐蚀的结果。
- 其他参数:
- shift_x, shift_y已弃用
自 0.23 版本弃用.
注释
对于
uint8``(以及在一定位深下的 ``uint16数据),较低的算法复杂度使得skimage.filters.rank.minimum()函数在处理较大图像和结构元素时更为高效。足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。对于偶数大小的结构元素,
skimage.morphology.binary_erosion()和此函数生成的输出会有所不同:一个相对于另一个偏移了一个像素。示例
>>> # Erosion shrinks bright regions >>> import numpy as np >>> from skimage.morphology import square >>> bright_square = np.array([[0, 0, 0, 0, 0], ... [0, 1, 1, 1, 0], ... [0, 1, 1, 1, 0], ... [0, 1, 1, 1, 0], ... [0, 0, 0, 0, 0]], dtype=np.uint8) >>> erosion(bright_square, square(3)) array([[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.flood(image, seed_point, *, footprint=None, connectivity=None, tolerance=None)[源代码][源代码]#
对应于泛洪填充的掩码。
从特定的 seed_point 开始,找到与种子值相等或在 tolerance 范围内的相连点。
- 参数:
- 图像ndarray
一个n维数组。
- seed_point元组或整数
用于 image 中作为泛洪填充起始点的点。如果图像是1D的,这个点可以作为一个整数给出。
- 足迹ndarray,可选
用于确定每个评估像素邻域的足迹(结构元素)。它必须仅包含1和0,并且与`image`具有相同的维度数。如果未给出,则所有相邻像素都被视为邻域的一部分(完全连接)。
- 连接性int, 可选
用于确定每个评估像素邻域的数值。与中心像素的平方距离小于或等于 connectivity 的相邻像素被视为邻居。如果 footprint 不为 None,则忽略此参数。
- 容差浮点数或整数,可选
如果为 None(默认),相邻值必须严格等于 seed_point 处 image 的初始值。这是最快的。如果给定一个值,将在每个点进行比较,如果与初始值在容差范围内也将被填充(包含)。
- 返回:
- 掩码ndarray
返回一个与 image 形状相同的布尔数组,其中与种子点相连且相等(或在容差范围内)的区域值为 True。所有其他值为 False。
注释
这个操作的概念类比是许多光栅图形程序中的’油漆桶’工具。这个函数只返回表示填充的掩码。
如果出于内存原因需要索引而不是掩码,用户可以简单地在结果上运行
numpy.nonzero,保存索引,并丢弃此掩码。示例
>>> from skimage.morphology import flood >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用5填充相连的部分,包括完全连接(包括对角线):
>>> mask = flood(image, (1, 1)) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
填充相连的点为5,不包括对角点(连接性1):
>>> mask = flood(image, (1, 1), connectivity=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
填充具有容差:
>>> mask = flood(image, (0, 0), tolerance=1) >>> image_flooded = image.copy() >>> image_flooded[mask] = 5 >>> image_flooded array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
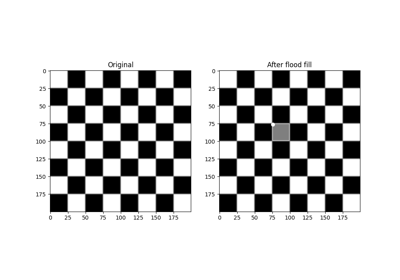
- skimage.morphology.flood_fill(image, seed_point, new_value, *, footprint=None, connectivity=None, tolerance=None, in_place=False)[源代码][源代码]#
对图像执行填充操作。
从特定的 seed_point 开始,找到与种子值相等或在其 tolerance 范围内的相连点,然后将其设置为 new_value。
- 参数:
- 图像ndarray
一个n维数组。
- seed_point元组或整数
用于 image 中作为泛洪填充起始点的点。如果图像是1D的,这个点可以作为一个整数给出。
- new_value : image 类型图像类型
新值用于设置整个填充。这必须与 image 的 dtype 一致选择。
- 足迹ndarray,可选
用于确定每个评估像素邻域的足迹(结构元素)。它必须仅包含1和0,并且与`image`具有相同的维度数。如果未给出,则所有相邻像素都被视为邻域的一部分(完全连接)。
- 连接性int, 可选
用于确定每个评估像素邻域的数值。与中心像素的平方距离小于或等于 connectivity 的相邻像素被视为邻居。如果 footprint 不为 None,则忽略此参数。
- 容差浮点数或整数,可选
如果为 None(默认),相邻值必须严格等于 seed_point 处的 image 值才能被填充。这是最快的。如果提供了容差,则填充值在种子点值的正负容差范围内的相邻点(包括边界)。
- in_placebool, 可选
如果为 True,则对 image 进行就地泛洪填充。如果为 False,则返回泛洪填充的结果而不修改输入的 `image`(默认)。
- 返回:
- 填充ndarray
返回一个与 image 形状相同的数组,其中与种子点相连且相等(或在容差范围内)的区域值被替换为 new_value。
注释
这个操作的概念类比是许多光栅图形程序中的’油漆桶’工具。
示例
>>> from skimage.morphology import flood_fill >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
用5填充相连的部分,包括完全连接(包括对角线):
>>> flood_fill(image, (1, 1), 5) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [5, 0, 0, 0, 0, 0, 3]])
填充相连的点为5,不包括对角点(连接性1):
>>> flood_fill(image, (1, 1), 5, connectivity=1) array([[0, 0, 0, 0, 0, 0, 0], [0, 5, 5, 0, 2, 2, 0], [0, 5, 5, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
填充具有容差:
>>> flood_fill(image, (0, 0), 5, tolerance=1) array([[5, 5, 5, 5, 5, 5, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 2, 2, 5], [5, 5, 5, 5, 5, 5, 3]])
- skimage.morphology.footprint_from_sequence(footprints)[源代码][源代码]#
将一个足迹序列转换为等效的 ndarray。
- 参数:
- 足迹2-元组的元组
一系列足迹元组,其中每个元组的第一个元素是对应于足迹的数组,第二个元素是它应被应用的次数。目前,所有足迹的大小都应为奇数。
- 返回:
- 足迹ndarray
一个等同于应用
footprints序列的单一数组。
- skimage.morphology.h_maxima(image, h, footprint=None)[源代码][源代码]#
确定图像中所有高度 >= h 的极大值。
局部最大值被定义为具有相同灰度级的像素的连通集,这些像素的灰度级严格大于集合直接邻域内所有像素的灰度级。
高度为 h 的局部最大值 M 是一个局部最大值,对于该最大值,存在至少一条路径将 M 与一个相等或更高的局部最大值连接起来,路径上的最小值为 f(M) - h(即路径上的值相对于最大值的值不会减少超过 h),并且不存在最小值更大的路径到达相等或更高的局部最大值。
该函数还能找到图像的全局最大值。
- 参数:
- 图像ndarray
要计算极大值的输入图像。
- h无符号整数
所有提取最大值的最小高度。
- 足迹ndarray,可选
以 n-D 数组表示的邻域,数组元素为 1 和 0。默认是根据最大范数(即对于 2D 图像为 3x3 的正方形,对于 3D 图像为 3x3x3 的立方体等)的半径为 1 的球体。
- 返回:
- h_maxndarray
高度 >= h 的局部最大值和全局最大值。生成的图像是二值图像,其中属于确定最大值的像素取值为 1,其他像素取值为 0。
参考文献
[1]Soille, P., “形态图像分析:原理与应用”(第6章),第二版(2003年),ISBN 3540429883。
示例
>>> import numpy as np >>> from skimage.morphology import extrema
我们创建一个图像(中心有一个最大值的二次函数和4个额外的常数最大值。最大值的高度为:1, 21, 41, 61, 81)
>>> w = 10 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:4,2:4] = 40; f[2:4,7:9] = 60; f[7:9,2:4] = 80; f[7:9,7:9] = 100 >>> f = f.astype(int)
我们可以计算所有高度至少为40的极大值:
>>> maxima = extrema.h_maxima(f, 40)
生成的图像将包含3个局部最大值。
- skimage.morphology.h_minima(image, h, footprint=None)[源代码][源代码]#
确定图像中深度 >= h 的所有最小值。
局部最小值被定义为具有相同灰度值且严格小于集合直接邻域内所有像素灰度值的像素连接集。
深度为 h 的局部最小值 M 是一个局部最小值,对于该最小值,存在至少一条路径将 M 与一个相等或更低的局部最小值连接起来,该路径上的最大值为 f(M) + h(即路径上的值相对于最小值的值不超过 h 的增加),并且不存在最大值更小的路径到达相等或更低的局部最小值。
该函数也能找到图像的全局最小值。
- 参数:
- 图像ndarray
要计算极小值的输入图像。
- h无符号整数
所有提取最小值的最小深度。
- 足迹ndarray,可选
以 n-D 数组表示的邻域,数组元素为 1 和 0。默认是根据最大范数(即对于 2D 图像为 3x3 的正方形,对于 3D 图像为 3x3x3 的立方体等)的半径为 1 的球体。
- 返回:
- h_minndarray
深度 >= h 的局部最小值和全局最小值。生成的图像是二值图像,其中属于确定的最小值的像素取值为1,其他像素取值为0。
参考文献
[1]Soille, P., “形态图像分析:原理与应用”(第6章),第二版(2003年),ISBN 3540429883。
示例
>>> import numpy as np >>> from skimage.morphology import extrema
我们创建一个图像(中心有一个最小值的二次函数和四个额外的常数最大值。最小值的深度为:1, 21, 41, 61, 81)
>>> w = 10 >>> x, y = np.mgrid[0:w,0:w] >>> f = 180 + 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:4,2:4] = 160; f[2:4,7:9] = 140; f[7:9,2:4] = 120; f[7:9,7:9] = 100 >>> f = f.astype(int)
我们可以计算所有深度至少为40的极小值:
>>> minima = extrema.h_minima(f, 40)
生成的图像将包含3个局部最小值。
- skimage.morphology.isotropic_closing(image, radius, out=None, spacing=None)[源代码][源代码]#
返回图像的二值形态学闭合。
此函数返回与二进制
skimage.morphology.binary_closing()相同的结果,但对于大型圆形结构元素执行速度更快。这是通过阈值化精确的欧几里得距离图 [1],[2] 实现的。实现基于scipy.ndimage.distance_transform_edt()。- 参数:
- 图像ndarray
二进制输入图像。
- 半径浮动
应闭合区域的半径。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递了 None,将分配一个新的数组。
- 间距float, 或 float 序列, 可选
每个维度上元素的间距。如果是一个序列,其长度必须等于输入的维度(轴的数量)。如果是一个单一数字,该值将用于所有轴。如果未指定,则隐含一个单位网格间距。
- 返回:
- 关闭布尔类型的 ndarray
形态学闭运算的结果。
参考文献
[1]Cuisenaire, O. 和 Macq, B., “利用传播的局部距离变换进行快速欧几里得形态学操作及其应用,” 图像处理及其应用, 1999. 第七届国际会议 (会议出版物编号 465), 1999, 第 856-860 页, 卷 2. DOI:10.1049/cp:19990446
[2]Ingemar Ragnemalm, 通过轮廓处理和距离图的阈值化实现快速腐蚀和膨胀, 模式识别快报, 第13卷, 第3期, 1992年, 第161-166页. DOI:10.1016/0167-8655(92)90055-5
- skimage.morphology.isotropic_dilation(image, radius, out=None, spacing=None)[源代码][源代码]#
返回图像的二值形态膨胀。
此函数返回与
skimage.morphology.binary_dilation()相同的结果,但对于较大的圆形结构元素执行速度更快。这是通过将阈值应用于反转图像的精确欧几里得距离图来实现的 [1], [2]。实现基于: func:scipy.ndimage.distance_transform_edt。- 参数:
- 图像ndarray
二进制输入图像。
- 半径浮动
区域应膨胀的半径。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 间距float, 或 float 序列, 可选
每个维度上元素的间距。如果是一个序列,其长度必须等于输入的维度(轴的数量)。如果是一个单一数字,该值将用于所有轴。如果未指定,则隐含一个单位网格间距。
- 返回:
- 扩张的布尔类型的 ndarray
形态学膨胀的结果,值在
[False, True]中。
参考文献
[1]Cuisenaire, O. 和 Macq, B., “利用传播的局部距离变换进行快速欧几里得形态学操作及其应用,” 图像处理及其应用, 1999. 第七届国际会议 (会议出版物编号 465), 1999, 第 856-860 页, 卷 2. DOI:10.1049/cp:19990446
[2]Ingemar Ragnemalm, 通过轮廓处理和距离图的阈值化实现快速腐蚀和膨胀, 模式识别快报, 第13卷, 第3期, 1992年, 第161-166页. DOI:10.1016/0167-8655(92)90055-5
- skimage.morphology.isotropic_erosion(image, radius, out=None, spacing=None)[源代码][源代码]#
返回图像的二值形态学腐蚀。
此函数返回与
skimage.morphology.binary_erosion()相同的结果,但对于较大的圆形结构元素执行速度更快。这是通过将阈值应用于图像的精确欧几里得距离图来实现的 [1], [2]。实现基于: func:scipy.ndimage.distance_transform_edt。- 参数:
- 图像ndarray
二进制输入图像。
- 半径浮动
区域应被侵蚀的半径。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果为 None,将分配一个新的数组。
- 间距float, 或 float 序列, 可选
每个维度上元素的间距。如果是一个序列,其长度必须等于输入的维度(轴的数量)。如果是一个单一数字,该值将用于所有轴。如果未指定,则隐含一个单位网格间距。
- 返回:
- 侵蚀布尔类型的 ndarray
形态学腐蚀的结果,取值在
[False, True]中。
参考文献
[1]Cuisenaire, O. 和 Macq, B., “利用传播的局部距离变换进行快速欧几里得形态学操作及其应用,” 图像处理及其应用, 1999. 第七届国际会议 (会议出版物编号 465), 1999, 第 856-860 页, 卷 2. DOI:10.1049/cp:19990446
[2]Ingemar Ragnemalm, 通过轮廓处理和距离图的阈值化实现快速腐蚀和膨胀, 模式识别快报, 第13卷, 第3期, 1992年, 第161-166页. DOI:10.1016/0167-8655(92)90055-5
- skimage.morphology.isotropic_opening(image, radius, out=None, spacing=None)[源代码][源代码]#
返回图像的二进制形态学开运算。
此函数返回与
skimage.morphology.binary_opening()相同的结果,但对于较大的圆形结构元素执行速度更快。这是通过阈值化精确的欧几里得距离图 [1]、[2] 实现的。实现基于scipy.ndimage.distance_transform_edt()。- 参数:
- 图像ndarray
二进制输入图像。
- 半径浮动
应打开区域的半径。
- 出布尔值的 ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 间距float, 或 float 序列, 可选
每个维度上元素的间距。如果是一个序列,其长度必须等于输入的维度(轴的数量)。如果是一个单一数字,该值将用于所有轴。如果未指定,则隐含一个单位网格间距。
- 返回:
- 已打开布尔类型的 ndarray
形态学开运算的结果。
参考文献
[1]Cuisenaire, O. 和 Macq, B., “利用传播的局部距离变换进行快速欧几里得形态学操作及其应用,” 图像处理及其应用, 1999. 第七届国际会议 (会议出版物编号 465), 1999, 第 856-860 页, 卷 2. DOI:10.1049/cp:19990446
[2]Ingemar Ragnemalm, 通过轮廓处理和距离图的阈值化实现快速腐蚀和膨胀, 模式识别快报, 第13卷, 第3期, 1992年, 第161-166页. DOI:10.1016/0167-8655(92)90055-5
- skimage.morphology.label(label_image, background=None, return_num=False, connectivity=None)[源代码][源代码]#
标记整数数组的连通区域。
两个像素在它们是邻居并且具有相同值时是连通的。在二维空间中,它们可以是1-连通或2-连通的。值指的是考虑一个像素/体素为邻居的最大正交跳数:
1-connectivity 2-connectivity diagonal connection close-up [ ] [ ] [ ] [ ] [ ] | \ | / | <- hop 2 [ ]--[x]--[ ] [ ]--[x]--[ ] [x]--[ ] | / | \ hop 1 [ ] [ ] [ ] [ ]
- 参数:
- label_imagedtype 为 int 的 ndarray
图像到标签。
- 背景int, 可选
将所有具有此值的像素视为背景像素,并将其标记为 0。默认情况下,值为 0 的像素被视为背景像素。
- return_numbool, 可选
是否返回分配的标签数量。
- 连接性int, 可选
考虑将一个像素/体素视为邻居的最大正交跳数。接受的值范围从 1 到 input.ndim。如果为
None,则使用input.ndim的完全连通性。
- 返回:
- 标签dtype 为 int 的 ndarray
标记数组,其中所有相连的区域都被赋予相同的整数值。
- numint, 可选
标签的数量,等于最大标签索引,仅当 return_num 为 True 时返回。
参考文献
[1]Christophe Fiorio 和 Jens Gustedt,“两种用于图像处理的线性时间并查策略”,《理论计算机科学》154卷(1996年),第165-181页。
[2]Kensheng Wu, Ekow Otoo 和 Arie Shoshani, “优化连通分量标记算法”, 论文 LBNL-56864, 2005, 劳伦斯伯克利国家实验室 (加利福尼亚大学), http://repositories.cdlib.org/lbnl/LBNL-56864
示例
>>> import numpy as np >>> x = np.eye(3).astype(int) >>> print(x) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, connectivity=1)) [[1 0 0] [0 2 0] [0 0 3]] >>> print(label(x, connectivity=2)) [[1 0 0] [0 1 0] [0 0 1]] >>> print(label(x, background=-1)) [[1 2 2] [2 1 2] [2 2 1]] >>> x = np.array([[1, 0, 0], ... [1, 1, 5], ... [0, 0, 0]]) >>> print(label(x)) [[1 0 0] [1 1 2] [0 0 0]]
- skimage.morphology.local_maxima(image, footprint=None, connectivity=None, indices=False, allow_borders=True)[源代码][源代码]#
查找 n 维数组的局部最大值。
局部最大值被定义为具有相同灰度级(平台)的像素的连通集,这些灰度级严格大于邻域中所有像素的灰度级。
- 参数:
- 图像ndarray
一个n维数组。
- 足迹ndarray,可选
用于确定每个评估像素邻域的足迹(结构元素)(
True表示连接的像素)。它必须是一个布尔数组,并且与 image 具有相同数量的维度。如果既没有给出 footprint 也没有给出 connectivity,则所有相邻像素都被视为邻域的一部分。- 连接性int, 可选
用于确定每个评估像素邻域的数值。与中心像素的平方距离小于或等于 connectivity 的相邻像素被视为邻居。如果 footprint 不为 None,则忽略此参数。
- 索引bool, 可选
如果为 True,输出将是一个一维数组的元组,表示每个维度中局部最大值的索引。如果为 False,输出将是一个布尔数组,其形状与 image 相同。
- allow_bordersbool, 可选
如果为真,接触图像边界的平台是有效最大值。
- 返回:
- 极大值ndarray 或 tuple[ndarray]
如果 indices 为 false,则返回一个与 image 形状相同的布尔数组,其中
True表示局部最大值的位置(否则为False)。如果 indices 为 true,则返回一个包含所有找到的最大值坐标的元组(索引)的一维数组。
- 警告:
- 用户警告
如果 allow_borders 为假,并且给定 image 的任何维度小于3个样本,则无法存在极大值,并显示警告。
注释
此函数基于以下思想运行:
首先在图像的最后一个维度上进行一次遍历,并通过仅在一个方向上比较像素来标记局部最大值的候选者。如果像素在最后一个维度上不相连,则所有像素都被标记为候选者。
对于每个候选人:
执行泛洪填充以找到所有具有相同灰度值且属于高原的相连像素。
考虑一个高原的连通邻域:如果没有相邻样本具有更高的灰度级,则将该高原标记为确定的局部最大值。
示例
>>> from skimage.morphology import local_maxima >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = 1 >>> image[3, 0] = 1 >>> image[1:3, 4:6] = 2 >>> image[3, 6] = 3 >>> image array([[0, 0, 0, 0, 0, 0, 0], [0, 1, 1, 0, 2, 2, 0], [0, 1, 1, 0, 2, 2, 0], [1, 0, 0, 0, 0, 0, 3]])
通过与所有相邻像素比较来找到局部最大值(最大连通性):
>>> local_maxima(image) array([[False, False, False, False, False, False, False], [False, True, True, False, False, False, False], [False, True, True, False, False, False, False], [ True, False, False, False, False, False, True]]) >>> local_maxima(image, indices=True) (array([1, 1, 2, 2, 3, 3]), array([1, 2, 1, 2, 0, 6]))
在不与对角像素比较的情况下找到局部最大值(连通性 1):
>>> local_maxima(image, connectivity=1) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [ True, False, False, False, False, False, True]])
并排除与图像边缘相邻的极大值:
>>> local_maxima(image, connectivity=1, allow_borders=False) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [False, False, False, False, False, False, False]])
- skimage.morphology.local_minima(image, footprint=None, connectivity=None, indices=False, allow_borders=True)[源代码][源代码]#
查找 n 维数组的局部最小值。
局部最小值被定义为具有相同灰度级(平台)的像素连接集,这些灰度级严格小于邻域中所有像素的灰度级。
- 参数:
- 图像ndarray
一个n维数组。
- 足迹ndarray,可选
用于确定每个评估像素邻域的足迹(结构元素)(
True表示连接的像素)。它必须是一个布尔数组,并且与 image 具有相同数量的维度。如果既没有给出 footprint 也没有给出 connectivity,则所有相邻像素都被视为邻域的一部分。- 连接性int, 可选
用于确定每个评估像素邻域的数值。与中心像素的平方距离小于或等于 connectivity 的相邻像素被视为邻居。如果 footprint 不为 None,则忽略此参数。
- 索引bool, 可选
如果为 True,输出将是一个一维数组的元组,表示每个维度中局部最小值的索引。如果为 False,输出将是一个布尔数组,其形状与 image 相同。
- allow_bordersbool, 可选
如果为真,接触图像边缘的平坦区域是有效的最小值。
- 返回:
- 最小值ndarray 或 tuple[ndarray]
如果 indices 为 false,将返回一个与 image 形状相同的布尔数组,其中
True表示局部最小值的位置(否则为False)。如果 indices 为 true,将返回一个包含所有找到的最小值坐标的元组,每个一维数组包含一个坐标(索引)。
注释
此函数基于以下思想运行:
首先遍历图像的最后一个维度,并通过仅在一个方向上比较像素来标记局部最小值的候选者。如果像素在最后一个维度上不相连,则所有像素都被标记为候选者。
对于每个候选人:
执行泛洪填充以找到所有具有相同灰度值且属于高原的相连像素。
考虑一个高原的连通邻域:如果没有相邻样本的灰度级更小,则将该高原标记为确定的局部最小值。
示例
>>> from skimage.morphology import local_minima >>> image = np.zeros((4, 7), dtype=int) >>> image[1:3, 1:3] = -1 >>> image[3, 0] = -1 >>> image[1:3, 4:6] = -2 >>> image[3, 6] = -3 >>> image array([[ 0, 0, 0, 0, 0, 0, 0], [ 0, -1, -1, 0, -2, -2, 0], [ 0, -1, -1, 0, -2, -2, 0], [-1, 0, 0, 0, 0, 0, -3]])
通过与所有相邻像素(最大连通性)进行比较来找到局部最小值:
>>> local_minima(image) array([[False, False, False, False, False, False, False], [False, True, True, False, False, False, False], [False, True, True, False, False, False, False], [ True, False, False, False, False, False, True]]) >>> local_minima(image, indices=True) (array([1, 1, 2, 2, 3, 3]), array([1, 2, 1, 2, 0, 6]))
在不与对角像素比较的情况下找到局部最小值(连通性 1):
>>> local_minima(image, connectivity=1) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [ True, False, False, False, False, False, True]])
并排除与图像边缘相邻的局部最小值:
>>> local_minima(image, connectivity=1, allow_borders=False) array([[False, False, False, False, False, False, False], [False, True, True, False, True, True, False], [False, True, True, False, True, True, False], [False, False, False, False, False, False, False]])
- skimage.morphology.max_tree(image, connectivity=1)[源代码][源代码]#
从图像中构建最大树。
组件树表示通过应用于图像的连续阈值操作得到的连接组件的层次结构。如果一个层次的组件包含在另一个层次的组件中,则前者是后者的父组件。最大树是组件树的一种高效表示。一个层次的连接组件由该层次的一个参考像素表示,该像素是该层次所有其他像素和上一层参考像素的父像素。最大树是许多形态学操作的基础,特别是连接操作。
- 参数:
- 图像ndarray
要计算最大树的输入图像。该图像可以是任何类型。
- 连接性无符号整数,可选
邻域连通性。整数表示到达邻居所需的最大正交步数。在2D中,4邻域为1,8邻域为2。默认值为1。
- 返回:
- 父级ndarray, int64
与图像形状相同的数组。每个像素的值是其父级在展平数组中的索引。
- tree_traverser1D 数组, int64
有序的像素索引(指向展平数组)。像素的排序方式是每个像素都紧随其父像素之后(根像素除外,因为它没有父像素)。
参考文献
[1]Salembier, P., Oliveras, A., & Garrido, L. (1998). 反扩展连通算子用于图像和序列处理。IEEE图像处理汇刊, 7(4), 555-570. DOI:10.1109/83.663500
[2]Berger, C., Geraud, T., Levillain, R., Widynski, N., Baillard, A., Bertin, E. (2007). 有效的组件树计算及其在天文图像模式识别中的应用。在国际图像处理会议 (ICIP) 上 (第41-44页). DOI:10.1109/ICIP.2007.4379949
[3]Najman, L., & Couprie, M. (2006). 构建准线性时间内的组件树。IEEE图像处理汇刊, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[4]Carlinet, E., & Geraud, T. (2014). 组件树计算算法比较综述. IEEE图像处理汇刊, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
示例
我们创建一个小样本图像(图1来自[4])并构建最大树。
>>> image = np.array([[15, 13, 16], [12, 12, 10], [16, 12, 14]]) >>> P, S = max_tree(image, connectivity=2)
- skimage.morphology.max_tree_local_maxima(image, connectivity=1, parent=None, tree_traverser=None)[源代码][源代码]#
确定图像的所有局部最大值。
局部最大值被定义为具有相同灰度值且严格大于集合直接邻域内所有像素灰度值的像素连接集。该函数标记局部最大值。
从技术上讲,该实现基于图像的最大树表示。如果最大树表示已经计算出来,该函数非常高效。否则,最好使用函数 local_maxima。
- 参数:
- 图像ndarray
要计算极大值的输入图像。
- 连接性无符号整数,可选
邻域连通性。整数表示到达邻居所需的最大正交步数。在2D中,4邻域为1,8邻域为2。默认值为1。
- 父级ndarray, int64, 可选
每个像素的值是其父级在展平数组中的索引。
- tree_traverser1D 数组, int64, 可选
有序的像素索引(指向展平数组)。像素的排序方式是每个像素都紧随其父像素之后(根像素除外,因为它没有父像素)。
- 返回:
- local_maxndarray, uint64
图像的标记局部最大值。
参考文献
[1]Vincent L., Proc. “灰度区域开闭运算,其高效实现及应用”, EURASIP 数学形态学及其在信号处理中的应用研讨会, 巴塞罗那, 西班牙, 第22-27页, 1993年5月。
[2]Soille, P., “形态图像分析:原理与应用” (第6章), 第二版 (2003), ISBN 3540429883. DOI:10.1007/978-3-662-05088-0
[3]Salembier, P., Oliveras, A., & Garrido, L. (1998). 反扩展连通算子用于图像和序列处理。IEEE图像处理汇刊, 7(4), 555-570. DOI:10.1109/83.663500
[4]Najman, L., & Couprie, M. (2006). 构建准线性时间内的组件树。IEEE图像处理汇刊, 15(11), 3531-3539. DOI:10.1109/TIP.2006.877518
[5]Carlinet, E., & Geraud, T. (2014). 组件树计算算法比较综述. IEEE图像处理汇刊, 23(9), 3885-3895. DOI:10.1109/TIP.2014.2336551
示例
我们创建一个图像(中心有一个最大值的二次函数和四个额外的恒定最大值)。
>>> w = 10 >>> x, y = np.mgrid[0:w,0:w] >>> f = 20 - 0.2*((x - w/2)**2 + (y-w/2)**2) >>> f[2:4,2:4] = 40; f[2:4,7:9] = 60; f[7:9,2:4] = 80; f[7:9,7:9] = 100 >>> f = f.astype(int)
我们可以计算所有局部最大值:
>>> maxima = max_tree_local_maxima(f)
生成的图像包含标记的局部最大值。
- skimage.morphology.medial_axis(image, mask=None, return_distance=False, *, rng=None)[源代码][源代码]#
计算二值图像的中轴变换。
- 参数:
- 图像二进制 ndarray,形状 (M, N)
要骨架化的形状的图像。如果此输入还不是二值图像,则将其转换为二值图像:在这种情况下,零值被视为背景(False),非零值被视为前景(True)。
- 掩码二进制 ndarray,形状 (M, N),可选
如果给定了掩码,则仅使用 image 中在 mask 中为真值的元素来计算中轴。
- return_distancebool, 可选
如果为真,距离变换也会与骨架一起返回。
- rng : {
numpy.random.Generator, int}, 可选toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。 伪随机数生成器。默认情况下,使用 PCG64 生成器(参见
numpy.random.default_rng())。如果 rng 是整数,则用于为生成器设定种子。PRNG 决定了在处理像素以打破平局时的顺序。
Added in version 0.19.
- 返回:
- 出布尔类型的 ndarray
图像的中轴变换
- dist整数 ndarray,可选
图像的距离变换(仅在 return_distance 为 True 时返回)
参见
注释
该算法通过图像的距离变换的脊线来计算图像的中轴变换。
- 算法的不同步骤如下
使用一个查找表,该表为每个3x3二进制方格的配置分配0或1,以决定中心像素是否应被移除或保留。我们希望一个点被移除,如果它有超过一个邻居,并且如果移除它不会改变连接组件的数量。
计算了到背景的距离变换,以及像素的角点度。
前景(值为1)的点根据距离变换排序,然后是角点。
调用一个 cython 函数将图像缩减为其骨架。它按照上一步确定的顺序处理像素,并根据查找表移除或保留像素。由于这种顺序,可以只通过一次处理所有像素。
示例
>>> square = np.zeros((7, 7), dtype=bool) >>> square[1:-1, 2:-2] = 1 >>> square.view(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> medial_axis(square).view(np.uint8) array([[0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.mirror_footprint(footprint)[源代码][源代码]#
在足迹中镜像每个维度。
- 参数:
- 足迹ndarray 或 元组
输入的足迹或足迹序列
- 返回:
- 倒置的ndarray 或 元组
沿每个维度镜像的足迹。
示例
>>> footprint = np.array([[0, 0, 0], ... [0, 1, 1], ... [0, 1, 1]], np.uint8) >>> mirror_footprint(footprint) array([[1, 1, 0], [1, 1, 0], [0, 0, 0]], dtype=uint8)
- skimage.morphology.octagon(m, n, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个八边形形状的焊盘。
对于给定的水平和垂直边长 (m) 以及给定的倾斜边高度或宽度 (n),生成一个八边形。倾斜边与水平轴成 45 或 135 度,因此宽度和高度相等。沿单个轴的占地面积总尺寸将为
m + 2 * n。- 参数:
- m整数
水平和垂直边的尺寸。
- n整数
斜边的长度或宽度。
- 返回:
- 足迹ndarray 或 元组
邻域元素为1,其他地方为0的足迹。当 decomposition 为 None 时,这只是一个 numpy.ndarray。否则,这将是一个元组,其长度等于要应用的唯一结构元素的数量(详见注释)
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘sequence’}, 可选
如果为 None,则返回一个数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但具有更好的计算性能。更多详情请参见注释。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。无论是二值还是灰度形态学,使用
decomposition='sequence'都被观察到具有性能优势,且随着足迹大小的增加,这种优势的幅度也会增加。
- skimage.morphology.octahedron(radius, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个八面体形状的足迹。
这是钻石的3D等价物。如果一个像素与邻域中心之间的城市街区/曼哈顿距离不大于半径,则该像素是邻域的一部分(即标记为1)。
- 参数:
- 半径整数
八面体形状的足迹的半径。
- 返回:
- 足迹ndarray 或 元组
邻域元素为1,其他地方为0的足迹。当 decomposition 为 None 时,这只是一个 numpy.ndarray。否则,这将是一个元组,其长度等于要应用的唯一结构元素的数量(详见注释)
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘sequence’}, 可选
如果为 None,则返回一个数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但具有更好的计算性能。更多详情请参见注释。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。无论是二值还是灰度形态学,使用
decomposition='sequence'都被观察到具有性能优势,且随着足迹大小的增加,这种优势的幅度也会增加。
- skimage.morphology.opening(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[源代码][源代码]#
返回图像的灰度形态学开运算。
图像的形态学开运算是定义为先腐蚀后膨胀的操作。开运算可以去除小的亮点(即“盐”)并连接小的暗裂缝。这往往会“打开”(暗)特征之间的(亮)间隙。
- 参数:
- 图像ndarray
图像数组。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式包括:’reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’, ‘max’, ‘min’, 或 ‘ignore’。如果选择 ‘ignore’,图像域外的像素被假设为图像数据类型的最大值用于腐蚀操作,最小值用于膨胀操作,这使得它们不会影响结果。默认值是 ‘reflect’。
- cval标量,可选
如果 mode 是 ‘constant’,则用于填充输入边缘之外的值。默认值为 0.0。
Added in version 0.23: mode 和 cval 在 0.23 版本中被添加。
- 返回:
- opening : 数组,形状和类型与 image 相同数组,形状和类型与
形态学开运算的结果。
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。示例
>>> # Open up gap between two bright regions (but also shrink regions) >>> import numpy as np >>> from skimage.morphology import square >>> bad_connection = np.array([[1, 0, 0, 0, 1], ... [1, 1, 0, 1, 1], ... [1, 1, 1, 1, 1], ... [1, 1, 0, 1, 1], ... [1, 0, 0, 0, 1]], dtype=np.uint8) >>> opening(bad_connection, square(3)) array([[0, 0, 0, 0, 0], [1, 1, 0, 1, 1], [1, 1, 0, 1, 1], [1, 1, 0, 1, 1], [0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.pad_footprint(footprint, *, pad_end=True)[源代码][源代码]#
将每个维度上的足迹填充为奇数大小。
- 参数:
- 足迹ndarray 或 元组
输入的足迹或足迹序列
- pad_endbool, 可选
如果
True,则在每个维度的末尾(右侧)填充,否则在前面(左侧)填充。
- 返回:
- 填充的ndarray 或 元组
每个维度上填充到奇数大小的足迹。
示例
>>> footprint = np.array([[0, 0], ... [1, 1], ... [1, 1]], np.uint8) >>> pad_footprint(footprint) array([[0, 0, 0], [1, 1, 0], [1, 1, 0]], dtype=uint8)
- skimage.morphology.reconstruction(seed, mask, method='dilation', footprint=None, offset=None)[源代码][源代码]#
对图像进行形态学重建。
通过膨胀进行形态学重建类似于基本的形态学膨胀:高强度值将替换附近的低强度值。然而,基本的膨胀操作符使用一个足迹来确定输入图像中的值可以传播多远。相比之下,重建使用两幅图像:一幅“种子”图像,它指定传播的值,以及一幅“掩码”图像,它给出每个像素允许的最大值。掩码图像,类似于足迹,限制了高强度值的传播。通过腐蚀进行的重建则是其逆过程:低强度值从种子图像传播,并由掩码图像限制,掩码图像表示允许的最小值。
或者,你可以将重建视为一种隔离图像中连接区域的方法。对于膨胀,重建连接由种子图像中局部最大值标记的区域:邻近像素小于或等于这些种子的像素被连接到种子区域。具有比种子图像更大值的局部最大值将被截断为种子值。
- 参数:
- 种子ndarray
种子图像(也称为标记图像),指定了将要进行膨胀或腐蚀的值。
- 掩码ndarray
每个像素允许的最大(膨胀)/最小(腐蚀)值。
- 方法{‘dilation’|’erosion’}, 可选
通过膨胀或腐蚀进行重建。在膨胀(或腐蚀)过程中,种子图像被膨胀(或腐蚀),直到被掩膜图像限制。对于膨胀,每个种子值必须小于或等于相应的掩膜值;对于腐蚀,情况相反。默认是’dilation’。
- 足迹ndarray,可选
以 n-D 数组表示的邻域,包含 1 和 0。默认是半径为 1 的 n-D 正方形(例如,对于 2D 图像为 3x3 正方形,对于 3D 图像为 3x3x3 立方体等)。
- 偏移量ndarray,可选
脚印中心点的坐标。默认位于脚印的几何中心,在这种情况下,脚印的尺寸必须是奇数。
- 返回:
- 重建的ndarray
形态重建的结果。
注释
该算法来自 [1]。灰度重建的应用在 [2] 和 [3] 中讨论。
参考文献
[1]Robinson, “高效形态重构:下坡滤波器”, 模式识别快报 25 (2004) 1759-1767.
[2]Vincent, L., “图像分析中的形态学灰度重构:应用和高效算法”,IEEE 图像处理汇刊 (1993)
[3]Soille, P., “形态图像分析:原理与应用”, 第六章, 第二版 (2003), ISBN 3540429883.
示例
>>> import numpy as np >>> from skimage.morphology import reconstruction
首先,我们创建一个正弦掩码图像,其峰值位于中间和两端。
>>> x = np.linspace(0, 4 * np.pi) >>> y_mask = np.cos(x)
然后,我们创建一个种子图像,初始化为最小掩码值(用于通过膨胀进行重建,最小强度值不会扩散),并在左右峰值处添加“种子”,但种子值为峰值值的一部分(1)。
>>> y_seed = y_mask.min() * np.ones_like(x) >>> y_seed[0] = 0.5 >>> y_seed[-1] = 0 >>> y_rec = reconstruction(y_seed, y_mask)
重建的图像(或在这种情况下为曲线)与掩码图像完全相同,只是峰值被截断为0.5和0。中间的峰值完全消失:由于该峰值区域没有种子值,其重建值被截断为周围值(-1)。
作为一个更实际的例子,我们尝试通过减去由重建创建的背景图像来提取图像的明亮特征。
>>> y, x = np.mgrid[:20:0.5, :20:0.5] >>> bumps = np.sin(x) + np.sin(y)
要创建背景图像,请将遮罩图像设置为原始图像,并将种子图像设置为原始图像,其强度偏移量为 h。
>>> h = 0.3 >>> seed = bumps - h >>> background = reconstruction(seed, bumps)
生成的重建图像看起来与原始图像完全相同,但凸起的峰值被切掉了。将这个重建图像从原始图像中减去,只剩下凸起的峰值。
>>> hdome = bumps - background
此操作被称为图像的 h-dome,并在减去的图像中保留高度为 h 的特征。
- skimage.morphology.rectangle(nrows, ncols, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个平坦的矩形形状的焊盘。
在给定宽度和高度生成的矩形中,每个像素都属于邻域。
- 参数:
- nrows整数
矩形的行数。
- ncols整数
矩形的列数。
- 返回:
- 足迹ndarray 或 元组
仅由1组成的足迹,即每个像素都属于邻域。当 decomposition 为 None 时,这只是一个 numpy.ndarray。否则,这将是一个元组,其长度等于要应用的唯一结构元素的数量(详见注释)。
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘separable’, ‘sequence’}, 可选
如果为 None,则返回一个单独的数组。对于 ‘sequence’,将返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但通常具有更好的计算性能。更多详情请参见注释。使用 ‘separable’ 时,此函数对每个轴使用可分离的 1D 足迹。’sequence’ 或 ‘separable’ 哪个计算速度更快可能取决于架构。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。对于二值形态学,使用
decomposition='sequence'被观察到能提供更好的性能,且性能提升的幅度随着结构元素大小的增加而迅速增加。对于带有矩形结构元素的灰度形态学,建议使用decomposition=None,因为所调用的内部 SciPy 函数已经基于可分离的 1D 滑动窗口实现了快速实现。sequence 分解模式仅支持奇数值的 nrows 和 ncols。如果 nrows 或 ncols 为偶数,则使用的序列将与
decomposition='separable'相同。在版本0.18.0中,
width和height的使用已被弃用。请改用nrows和ncols。
- skimage.morphology.remove_objects_by_distance(label_image, min_distance, *, priority=None, p_norm=2, spacing=None, out=None)[源代码][源代码]#
按指定顺序移除对象,直到剩余对象之间的距离达到最小。
从图像中移除标记的对象,直到剩余的对象之间的距离超过给定的距离。默认情况下,首先移除较小的对象。
- 参数:
- label_image整数的ndarray
一个包含对象标签的 n 维数组,例如由
label()返回的。值为零的被视为背景,所有其他对象 ID 必须是正整数。- min_distanceint 或 float
移除与其他对象的距离不超过此正值的对象。优先级较低的对象首先被移除。
- 优先级ndarray,可选
定义对象被移除的优先级。期望一个长度为
np.amax(label_image) + 1的一维数组,其中包含每个对象标签在相应索引处的优先级。优先级较低的对象首先被移除,直到所有剩余对象都满足距离要求。如果没有给出,优先级将给予样本数量较多且标签值次之的对象。- p_normint 或 float, 可选
Minkowski距离的p阶,用于计算对象之间的距离。默认值``2``对应于欧几里得距离,``1``对应于“曼哈顿”距离,``np.inf``对应于切比雪夫距离。
- 间距浮点数序列,可选
label_image 沿每个轴的像素间距。如果未指定,则隐含单位(1)的网格间距。
- 出ndarray,可选
与 image 形状和数据类型相同的数组,输出将被放置在其中。默认情况下,会创建一个新的数组。
- 返回:
- 出ndarray
与 label_image 形状相同的数组,其中违反了 min_distance 条件的对象已被移除。
参见
skimage.morphology.remove_small_objects移除小于指定尺寸的对象。
注释
该算法的基本步骤如下:
找到所有给定对象的索引,并根据它们是否指向对象的边界来分离它们。
按标签值对索引进行排序,确保指向同一对象的索引彼此相邻。这种优化使得只需跳转到相邻的索引即可找到对象的所有部分。
按 priority 排序边界索引。使用稳定排序以保留前一步排序的顺序。如果未给出 priority,则使用
numpy.bincount()作为回退。从边界索引构建
scipy.spatial.cKDTree。按优先排序的顺序遍历边界索引,并查询 kd-tree 以获取距离过近的对象。移除这些对象,并在后续评估其他对象时不考虑它们。
该算法的性能取决于 label_image 中属于物体边界的样本数量。
示例
>>> import skimage as ski >>> ski.morphology.remove_objects_by_distance(np.array([2, 0, 1, 1]), 2) array([0, 0, 1, 1]) >>> ski.morphology.remove_objects_by_distance( ... np.array([2, 0, 1, 1]), 2, priority=np.array([0, 1, 9]) ... ) array([2, 0, 0, 0]) >>> label_image = np.array( ... [[8, 0, 0, 0, 0, 0, 0, 0, 0, 9, 9], ... [8, 8, 8, 0, 0, 0, 0, 0, 0, 9, 9], ... [0, 0, 0, 0, 0, 0, 0, 0, 9, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], ... [0, 0, 3, 0, 0, 0, 1, 0, 0, 0, 0], ... [2, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], ... [0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 7]] ... ) >>> ski.morphology.remove_objects_by_distance( ... label_image, min_distance=3 ... ) array([[8, 0, 0, 0, 0, 0, 0, 0, 0, 9, 9], [8, 8, 8, 0, 0, 0, 0, 0, 0, 9, 9], [0, 0, 0, 0, 0, 0, 0, 0, 9, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 7]])
- skimage.morphology.remove_small_holes(ar, area_threshold=64, connectivity=1, *, out=None)[源代码][源代码]#
移除小于指定尺寸的连续孔洞。
- 参数:
- arndarray(任意形状,int 或 bool 类型)
包含感兴趣的连通分量的数组。
- area_thresholdint, 可选 (默认值: 64)
将被填充的连续孔洞的最大面积,以像素为单位。替代 min_size。
- 连接性int, {1, 2, …, ar.ndim}, 可选 (默认: 1)
定义像素邻域的连通性。
- 出ndarray
与 ar 形状相同且具有 bool 类型的数组,输出将被放置在其中。默认情况下,会创建一个新数组。
- 返回:
- out : ndarray, 与输入 ar 形状和类型相同ndarray,形状和类型与输入相同
移除了连通组件内小孔的输入数组。
- Raises:
- 类型错误
如果输入数组的类型无效,例如浮点数或字符串。
- ValueError
如果输入数组包含负值。
注释
如果数组类型是 int,则假定它包含已经标记的对象。标签不会保留在输出图像中(此函数始终输出布尔图像)。建议在使用此函数后完成标记。
示例
>>> from skimage import morphology >>> a = np.array([[1, 1, 1, 1, 1, 0], ... [1, 1, 1, 0, 1, 0], ... [1, 0, 0, 1, 1, 0], ... [1, 1, 1, 1, 1, 0]], bool) >>> b = morphology.remove_small_holes(a, 2) >>> b array([[ True, True, True, True, True, False], [ True, True, True, True, True, False], [ True, False, False, True, True, False], [ True, True, True, True, True, False]]) >>> c = morphology.remove_small_holes(a, 2, connectivity=2) >>> c array([[ True, True, True, True, True, False], [ True, True, True, False, True, False], [ True, False, False, True, True, False], [ True, True, True, True, True, False]]) >>> d = morphology.remove_small_holes(a, 2, out=a) >>> d is a True
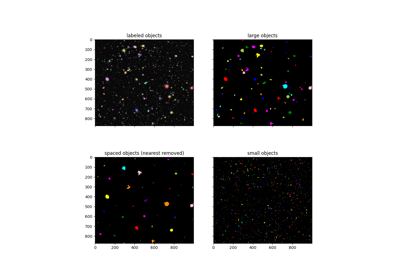
- skimage.morphology.remove_small_objects(ar, min_size=64, connectivity=1, *, out=None)[源代码][源代码]#
移除小于指定尺寸的对象。
期望 ar 是一个带有标签对象的数组,并移除小于 min_size 的对象。如果 ar 是布尔值,图像首先会被标记。这导致布尔值和 0-1 数组可能会有不同的行为。
- 参数:
- arndarray(任意形状,int 或 bool 类型)
包含感兴趣对象的数组。如果数组类型是整数,则整数必须为非负数。
- min_sizeint, 可选 (默认值: 64)
允许的最小对象大小。
- 连接性int, {1, 2, …, ar.ndim}, 可选 (默认: 1)
定义像素邻域的连通性。如果在标记过程中 ar 是布尔值,则使用。
- 出ndarray
与 ar 形状相同的数组,输出将被放置在其中。默认情况下,会创建一个新数组。
- 返回:
- out : ndarray, 与输入 ar 形状和类型相同ndarray,形状和类型与输入相同
移除了小连通分量的输入数组。
- Raises:
- 类型错误
如果输入数组的类型无效,例如浮点数或字符串。
- ValueError
如果输入数组包含负值。
示例
>>> from skimage import morphology >>> a = np.array([[0, 0, 0, 1, 0], ... [1, 1, 1, 0, 0], ... [1, 1, 1, 0, 1]], bool) >>> b = morphology.remove_small_objects(a, 6) >>> b array([[False, False, False, False, False], [ True, True, True, False, False], [ True, True, True, False, False]]) >>> c = morphology.remove_small_objects(a, 7, connectivity=2) >>> c array([[False, False, False, True, False], [ True, True, True, False, False], [ True, True, True, False, False]]) >>> d = morphology.remove_small_objects(a, 6, out=a) >>> d is a True
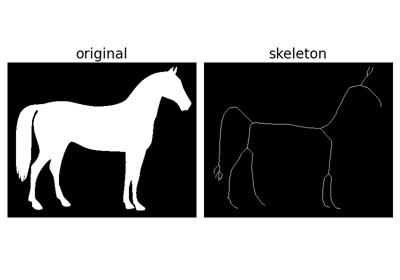
- skimage.morphology.skeletonize(image, *, method=None)[源代码][源代码]#
计算二值图像的骨架。
细化用于将二值图像中的每个连通分量减少为一个单像素宽的骨架。
- 参数:
- 返回:
- 骨架布尔类型的 ndarray
细化后的图像。
参见
参考文献
[Lee94]T.-C. Lee, R.L. Kashyap 和 C.-N. Chu, 通过 3-D 中轴/骨架细化算法构建骨架模型。计算机视觉、图形和图像处理, 56(6):462-478, 1994.
[Zha84]一种用于细化数字模式的快速并行算法,T. Y. Zhang 和 C. Y. Suen,《ACM 通讯》,1984年3月,第27卷,第3期。
示例
>>> X, Y = np.ogrid[0:9, 0:9] >>> ellipse = (1./3 * (X - 4)**2 + (Y - 4)**2 < 3**2).astype(bool) >>> ellipse.view(np.uint8) array([[0, 0, 0, 1, 1, 1, 0, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 1, 1, 0, 0], [0, 0, 0, 1, 1, 1, 0, 0, 0]], dtype=uint8) >>> skel = skeletonize(ellipse) >>> skel.view(np.uint8) array([[0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.square(width, dtype=<class 'numpy.uint8'>, *, decomposition=None)[源代码][源代码]#
生成一个扁平的、方形的外形。
沿着周长的每个像素的棋盘距离不超过半径(radius=floor(width/2))像素。
- 参数:
- 宽度整数
正方形的宽度和高度。
- 返回:
- 足迹ndarray 或 元组
邻域元素为1,其他地方为0的足迹。当 decomposition 为 None 时,这只是一个 numpy.ndarray。否则,这将是一个元组,其长度等于要应用的唯一结构元素的数量(详见注释)
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- 分解{None, ‘separable’, ‘sequence’}, 可选
如果为 None,则返回一个单一数组。对于 ‘sequence’,返回一个较小的足迹元组。应用这一系列较小的足迹将得到与单个较大足迹相同的结果,但通常具有更好的计算性能。更多详情请参见注释。使用 ‘separable’ 时,此函数对每个轴使用可分离的 1D 足迹。’sequence’ 或 ‘separable’ 哪个计算速度更快可能取决于架构。
注释
当 decomposition 不为 None 时,footprint 元组的每个元素都是一个形如
(ndarray, num_iter)的 2-元组,指定了一个 footprint 数组及其要应用的迭代次数。对于二值形态学,使用
decomposition='sequence'或decomposition='separable'观察到比decomposition=None更好的性能,性能提升的幅度随着足迹大小的增加而迅速增加。对于带有方形足迹的灰度形态学,建议使用decomposition=None,因为所调用的内部 SciPy 函数已经基于可分离的 1D 滑动窗口实现了快速实现。“序列”分解模式仅支持奇数值的 width。如果 width 是偶数,所使用的序列将与“可分离”模式相同。
- skimage.morphology.star(a, dtype=<class 'numpy.uint8'>)[源代码][源代码]#
生成一个星形焊盘。
Start 有8个顶点,并且是一个大小为 2*a + 1 的正方形与其45度旋转版本的叠加。斜边与水平轴成45度或135度。
- 参数:
- a整数
决定星形结构元素大小的参数。返回的方形数组的边长为 2*a + 1 + 2*floor(a / 2)。
- 返回:
- 足迹ndarray
邻域元素为1,其他地方为0的足迹。
- 其他参数:
- dtype数据类型,可选
足迹的数据类型。
- skimage.morphology.thin(image, max_num_iter=None)[源代码][源代码]#
对二值图像进行形态学细化。
- 参数:
- 图像二进制 (M, N) ndarray
要细化的图像。如果此输入还不是二值图像,则将其转换为二值图像:在这种情况下,零值被视为背景(False),非零值被视为前景(True)。
- max_num_iterint, 迭代次数, 可选
无论此参数的值如何,如果一次迭代没有产生变化,则立即返回细化图像。如果指定了此参数,则它因此设置了执行的迭代次数的上限。
- 返回:
- 出布尔类型的 ndarray
薄化图像。
注释
该算法 [1] 通过多次遍历图像,移除符合一组设计用于细化连接区域的标准像素,同时保留八连通分量和2 x 2的正方形 [2]。在每次迭代中,算法将中间的骨架图像与邻域掩码相关联,然后查找每个邻域在查找表中,指示在该子迭代中是否应删除中心像素。
参考文献
[1]Z. Guo and R. W. Hall, “Parallel thinning with two-subiteration algorithms,” Comm. ACM, vol. 32, no. 3, pp. 359-373, 1989. DOI:10.1145/62065.62074
[2]Lam, L., Seong-Whan Lee, 和 Ching Y. Suen, “细化方法综述,” IEEE模式分析与机器智能汇刊, 第14卷, 第9期, 第879页, 1992年. DOI:10.1109/34.161346
示例
>>> square = np.zeros((7, 7), dtype=bool) >>> square[1:-1, 2:-2] = 1 >>> square[0, 1] = 1 >>> square.view(np.uint8) array([[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8) >>> skel = thin(square) >>> skel.view(np.uint8) array([[0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0]], dtype=uint8)
- skimage.morphology.white_tophat(image, footprint=None, out=None, *, mode='reflect', cval=0.0)[源代码][源代码]#
返回图像的白色顶帽。
图像的白色顶部帽子定义为图像减去其形态学开运算。此操作返回图像中比结构元素小的亮斑。
- 参数:
- 图像ndarray
图像数组。
- 足迹ndarray 或 元组,可选
以二维数组表示的邻域,数组中包含1和0。如果为None,则使用十字形足迹(connectivity=1)。足迹也可以作为一系列较小的足迹提供,如下面注释中所述。
- 出ndarray,可选
用于存储形态学结果的数组。如果传递 None,将分配一个新数组。
- 模式str, 可选
mode 参数决定了如何处理数组边界。有效的模式有:’reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’, ‘max’, ‘min’, 或 ‘ignore’。参见
skimage.morphology.opening()。默认是 ‘reflect’。- cval标量,可选
如果 mode 是 ‘constant’,则用于填充输入边缘之外的值。默认值为 0.0。
Added in version 0.23: mode 和 cval 在 0.23 版本中被添加。
- 返回:
- out : 数组, 与 image 形状和类型相同数组,形状和类型与
形态学白帽操作的结果。
参见
注释
足迹也可以作为一系列2元组提供,其中每个2元组的第一个元素是一个足迹ndarray,第二个元素是一个整数,描述它应该迭代的次数。例如
footprint=[(np.ones((9, 1)), 1), (np.ones((1, 9)), 1)]将应用一个9x1的足迹,然后是一个1x9的足迹,产生的效果与footprint=np.ones((9, 9))相同,但计算成本较低。大多数内置的足迹,如skimage.morphology.disk()提供了自动生成这种类型足迹序列的选项。参考文献
示例
>>> # Subtract gray background from bright peak >>> import numpy as np >>> from skimage.morphology import square >>> bright_on_gray = np.array([[2, 3, 3, 3, 2], ... [3, 4, 5, 4, 3], ... [3, 5, 9, 5, 3], ... [3, 4, 5, 4, 3], ... [2, 3, 3, 3, 2]], dtype=np.uint8) >>> white_tophat(bright_on_gray, square(3)) array([[0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 1, 5, 1, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 0]], dtype=uint8)