skimage.filters#
对 |
|
应用一个巴特沃斯滤波器来增强高频或低频特征。 |
|
计算 padded_array 和 kernel 的有效互相关。 |
|
在大小中找到介于 |
|
使用 Farid 变换找到边缘幅度。 |
|
使用 Farid 变换查找图像的水平边缘。 |
|
使用 Farid 变换查找图像的垂直边缘。 |
|
应用给定的过滤器到数据。 |
|
对给定数据应用反向过滤器。 |
|
使用Frangi血管滤波器对图像进行滤波。 |
|
返回Gabor滤波器的实部和虚部响应。 |
|
返回复杂的二维Gabor滤波器核。 |
|
多维高斯滤波器。 |
|
使用混合Hessian滤波器对图像进行滤波。 |
|
使用拉普拉斯算子找到图像的边缘。 |
|
返回图像的局部中值。 |
|
使用 Meijering 神经滤波器过滤图像。 |
|
使用Prewitt变换找到边缘幅度。 |
|
使用 Prewitt 变换查找图像的水平边缘。 |
|
使用 Prewitt 变换查找图像的垂直边缘。 |
|
返回一个与原图像形状相同的图像,其中每个像素是该像素值在 |
|
使用Roberts交叉算子寻找边缘幅度。 |
|
使用Roberts' Cross算子查找图像的交叉边缘。 |
|
使用Roberts交叉算子查找图像的交叉边缘。 |
|
使用Sato管状滤波器过滤图像。 |
|
使用Scharr变换查找边缘幅度。 |
|
使用 Scharr 变换查找图像的水平边缘。 |
|
使用 Scharr 变换查找图像的垂直边缘。 |
|
使用Sobel滤波器在图像中寻找边缘。 |
|
使用 Sobel 变换找到图像的水平边缘。 |
|
使用Sobel变换查找图像的垂直边缘。 |
|
基于ISODATA方法返回阈值。 |
|
通过Li的迭代最小交叉熵方法计算阈值。 |
|
基于局部像素邻域计算一个阈值掩码图像。 |
|
基于灰度值的平均值返回阈值。 |
|
基于最小方法返回阈值。 |
|
生成 classes-1 个阈值,以根据 Otsu 的多类方法分割 图像 中的灰度级。 |
|
对数组应用Niblack局部阈值。 |
|
基于大津法返回阈值。 |
|
对数组应用 Sauvola 局部阈值。 |
|
基于三角算法返回阈值。 |
|
基于Yen方法返回阈值。 |
|
返回一个比较不同阈值方法输出的图形。 |
|
非锐化掩模滤镜。 |
|
最小均方误差(维纳)逆滤波器。 |
|
返回一个给定大小和维度的n维窗口。 |
|
线性位置不变滤波器(二维) |
|
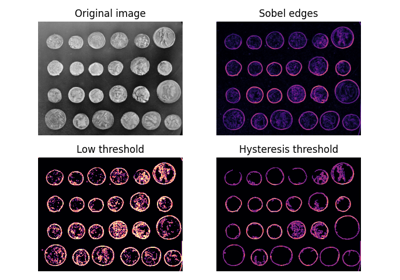
- skimage.filters.apply_hysteresis_threshold(image, low, high)[源代码][源代码]#
对
image应用滞后阈值处理。该算法找到
image大于high或image大于low且该区域与大于high的区域相连的区域。- 参数:
- 图像(M[, …]) ndarray
灰度输入图像。
- low : float, 或与
image形状相同的数组浮点数,或与输入形状相同的数组 较低的阈值。
- 高 : 浮点数,或与
image形状相同的数组浮点数,或与输入形状相同的数组 更高阈值。
- 返回:
- 阈值化(M[, …]) 布尔数组
数组,其中
True表示image高于滞后阈值的位置。
参考文献
[1]J. Canny. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1986; vol. 8, pp.679-698. DOI:10.1109/TPAMI.1986.4767851
示例
>>> image = np.array([1, 2, 3, 2, 1, 2, 1, 3, 2]) >>> apply_hysteresis_threshold(image, 1.5, 2.5).astype(int) array([0, 1, 1, 1, 0, 0, 0, 1, 1])
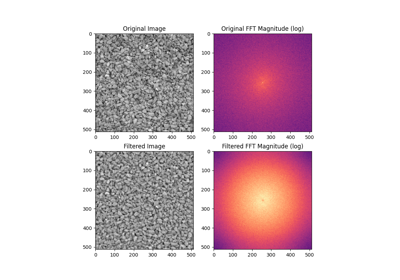
- skimage.filters.butterworth(image, cutoff_frequency_ratio=0.005, high_pass=True, order=2.0, channel_axis=None, *, squared_butterworth=True, npad=0)[源代码][源代码]#
应用一个巴特沃斯滤波器来增强高频或低频特征。
此滤波器在傅里叶域中定义。
- 参数:
- 图像(M[, N[, …, P]][, C]) ndarray
输入图像。
- 截止频率比率float, 可选
确定截止位置相对于 FFT 形状的位置。接收一个介于 [0, 0.5] 之间的值。
- 高通bool, 可选
是否执行高通滤波。如果为 False,则执行低通滤波。
- 顺序float, 可选
影响截止点附近斜率的滤波器顺序。更高的顺序意味着在频率空间中更陡的斜率。
- channel_axisint, 可选
如果有通道维度,请在此处提供索引。如果为 None(默认),则假定所有轴都是空间维度。
- squared_butterworthbool, 可选
当为 True 时,使用巴特沃斯滤波器的平方。更多详情请参见下文。
- npadint, 可选
使用
numpy.pad的mode='edge'扩展,在图像的每个边缘填充 npad 像素。
- 返回:
- 结果ndarray
经过巴特沃斯滤波的图像。
注释
带通滤波器可以通过结合高通滤波器和低通滤波器来实现。如果出现边界伪影,用户可以增加 npad。
图像处理教科书中使用的“巴特沃斯滤波器”(例如 [1],[2])通常是传统巴特沃斯滤波器的平方,如 [3],[4] 所述。如果 squared_butterworth 设置为
True,将使用平方版本。低通平方巴特沃斯滤波器在低通情况下由以下表达式给出:\[H_{low}(f) = \frac{1}{1 + \left(\frac{f}{c f_s}\right)^{2n}}\]在给定高通滤波器的情况下
\[H_{hi}(f) = 1 - H_{low}(f)\]其中 \(f=\sqrt{\sum_{d=0}^{\mathrm{ndim}} f_{d}^{2}}\) 是空间频率的绝对值,\(f_s\) 是采样频率,\(c\) 是
cutoff_frequency_ratio,\(n\) 是滤波器 order [1]。当squared_butterworth=False时,使用上述表达式的平方根。注意,
cutoff_frequency_ratio是根据采样频率 \(f_s\) 定义的。FFT 频谱覆盖了奈奎斯特范围(\([-f_s/2, f_s/2]\)),因此cutoff_frequency_ratio的值应在 0 到 0.5 之间。当squared_butterworth为真时,截止频率处的频率响应(增益)为 0.5,当其为假时,增益为 \(1/\sqrt{2}\)。参考文献
[2]Birchfield, Stan. 图像处理与分析. 2018. Cengage Learning.
[3]Butterworth, Stephen. “关于滤波放大器的理论。” 无线工程师 7.6 (1930): 536-541.
示例
分别对灰度图像和彩色图像应用高通和低通巴特沃斯滤波器:
>>> from skimage.data import camera, astronaut >>> from skimage.filters import butterworth >>> high_pass = butterworth(camera(), 0.07, True, 8) >>> low_pass = butterworth(astronaut(), 0.01, False, 4, channel_axis=-1)
- skimage.filters.correlate_sparse(image, kernel, mode='reflect')[源代码][源代码]#
计算 padded_array 和 kernel 的有效互相关。
当 kernel 很大且包含许多零时,此函数是 快速 的。
参见
scipy.ndimage.correlate以了解互相关的描述。- 参数:
- 图像ndarray, dtype float, 形状 (M, N[, …], P)
输入数组。如果模式是 ‘valid’,这个数组应该已经填充,因为将剥离与核相同形状的边缘。
- 内核ndarray, dtype float, 形状 (Q, R[, …], S)
要进行相关运算的内核。必须与 padded_array 具有相同的维度。为了高性能,它应该是稀疏的(非零元素较少)。
- 模式字符串,可选
参见
scipy.ndimage.correlate以获取有效的模式。此外,模式 ‘valid’ 也被接受,在这种情况下不应用填充,结果是对于内核完全位于原始数据内部的小图像的结果。
- 返回:
- 结果浮点数数组,形状为 (M, N[, …], P)
将 image 与 kernel 进行互相关运算的结果。如果使用模式 ‘valid’,结果的形状为 (M-Q+1, N-R+1[, …], P-S+1)。
- skimage.filters.difference_of_gaussians(image, low_sigma, high_sigma=None, *, mode='nearest', cval=0, channel_axis=None, truncate=4.0)[源代码][源代码]#
在大小中找到介于
low_sigma和high_sigma之间的特征。此函数使用高斯差分方法对多维数组应用带通滤波器。输入数组使用两个不同标准差的高斯核进行模糊处理,生成两个中间的滤波图像。然后将较模糊的图像从较不模糊的图像中减去。因此,最终的输出图像将通过较小标准差的高斯核衰减高频分量,而低频分量将被移除,因为它们存在于较模糊的中间图像中。
- 参数:
- 图像ndarray
要过滤的输入数组。
- low_sigma标量或标量序列
所有轴上较小 sigma 的高斯核的标准偏差。标准偏差作为序列给出,或作为单个数字给出,在这种情况下,单个数字用作所有轴的标准偏差值。
- 高_sigma标量或标量序列,可选(默认值为 None)
高斯核在所有轴上的较大标准差的标准差。标准差以序列形式给出,或作为单个数字给出,在这种情况下,单个数字被用作所有轴的标准差值。如果给定 None(默认),则所有轴的标准差计算为 1.6 * low_sigma。
- 模式{‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’},可选
mode参数决定了数组边界的处理方式,其中cval是当 mode 等于 ‘constant’ 时的值。默认值是 ‘nearest’。- cval标量,可选
如果
mode是 ‘constant’,则填充输入边缘之外的值。默认值为 0.0。- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19:
channel_axis在 0.19 版本中被添加。- 截断float, 可选 (默认值为 4.0)
将过滤器截断为此数量的标准差。
- 返回:
- filtered_imagendarray
过滤后的数组。
注释
此函数将从使用由
high_sigma提供的标准差的高斯核过滤的数组中,减去使用由low_sigma提供的标准差的高斯核过滤的数组。high_sigma的值必须始终大于或等于low_sigma中相应的值,否则将引发ValueError。当
high_sigma为空时,high_sigma的值将计算为low_sigma中相应值的 1.6 倍。这个比例最初由 Marr 和 Hildreth (1980) [1] 提出,并在近似高斯拉普拉斯逆运算时通常使用,该运算用于边缘和斑点检测。输入图像根据
img_as_float的约定进行转换。除了 sigma 值外,所有参数都用于两种过滤器。
参考文献
[1]Marr, D. 和 Hildreth, E. 边缘检测理论。Proc. R. Soc. Lond. Series B 207, 187-217 (1980). https://doi.org/10.1098/rspb.1980.0020
示例
对彩色图像应用简单的高斯差分滤波器:
>>> from skimage.data import astronaut >>> from skimage.filters import difference_of_gaussians >>> filtered_image = difference_of_gaussians(astronaut(), 2, 10, ... channel_axis=-1)
应用一个由高斯差分滤波器近似的拉普拉斯高斯滤波器:
>>> filtered_image = difference_of_gaussians(astronaut(), 2, ... channel_axis=-1)
对灰度图像应用高斯差分滤波器,为每个轴使用不同的sigma值:
>>> from skimage.data import camera >>> filtered_image = difference_of_gaussians(camera(), (2,5), (3,20))
- skimage.filters.farid(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[源代码][源代码]#
使用 Farid 变换找到边缘幅度。
- 参数:
- 图像数组
输入图像。
- 掩码布尔数组,可选
将输出图像裁剪到此掩码。(掩码=0 的值将被设置为 0。)
- 轴int 或 int 序列,可选
计算沿此轴的边缘滤波器。如果未提供,则计算边缘幅度。定义如下:
farid_mag = np.sqrt(sum([farid(image, axis=i)**2 for i in range(image.ndim)]) / image.ndim)
如果轴是一个序列,也会计算大小。
- 模式str 或 str 序列,可选
卷积的边界模式。有关模式的描述,请参见
scipy.ndimage.convolve。这可以是单一的边界模式,也可以是每个轴一个边界模式。- cvalfloat, 可选
当 mode 为
'constant'时,这是在图像数据边界之外的值中使用的常数。
- 返回:
- 输出浮点数数组
Farid 边缘图。
注释
取水平和垂直导数的平方和的平方根,以得到一个对方向不太敏感的幅度。类似于Scharr算子,此算子设计时考虑了旋转不变性约束。
参考文献
[1]Farid, H. 和 Simoncelli, E. P., “离散多维信号的微分”, IEEE Transactions on Image Processing 13(4): 496-508, 2004. DOI:10.1109/TIP.2004.823819
[2]维基百科,“Farid 和 Simoncelli 导数。” 可访问于:<https://en.wikipedia.org/wiki/Image_derivatives#Farid_and_Simoncelli_Derivatives>
示例
>>> from skimage import data >>> camera = data.camera() >>> from skimage import filters >>> edges = filters.farid(camera)
- skimage.filters.farid_h(image, *, mask=None)[源代码][源代码]#
使用 Farid 变换查找图像的水平边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Farid 边缘图。
注释
内核是使用 [1] 中的 5-tap 权重构建的。
参考文献
[1]Farid, H. 和 Simoncelli, E. P., “离散多维信号的微分”, IEEE Transactions on Image Processing 13(4): 496-508, 2004. DOI:10.1109/TIP.2004.823819
[2]Farid, H. 和 Simoncelli, E. P. “最优旋转等变方向导数核”,收录于:第七届国际计算机图像与模式分析会议,德国基尔。1997年9月。
- skimage.filters.farid_v(image, *, mask=None)[源代码][源代码]#
使用 Farid 变换查找图像的垂直边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Farid 边缘图。
注释
内核是使用 [1] 中的 5-tap 权重构建的。
参考文献
[1]Farid, H. 和 Simoncelli, E. P., “离散多维信号的微分”, IEEE Transactions on Image Processing 13(4): 496-508, 2004. DOI:10.1109/TIP.2004.823819
- skimage.filters.filter_forward(data, impulse_response=None, filter_params=None, predefined_filter=None)[源代码][源代码]#
应用给定的过滤器到数据。
- 参数:
- 数据(M, N) ndarray
输入数据。
- impulse_response : 可调用对象 f(r, c, **filter_params)可调用
滤波器的脉冲响应。参见 LPIFilter2D.__init__。
- filter_paramsdict, 可选
impulse_response 函数的附加关键字参数。
- 其他参数:
- 预定义过滤器LPIFilter2D
如果你需要在不同的图像上多次应用相同的滤波器,请构造 LPIFilter2D 并在此处指定它。
示例
未归一化的高斯滤波器:
>>> def filt_func(r, c, sigma=1): ... return np.exp(-(r**2 + c**2)/(2 * sigma**2)) >>> >>> from skimage import data >>> filtered = filter_forward(data.coins(), filt_func)
- skimage.filters.filter_inverse(data, impulse_response=None, filter_params=None, max_gain=2, predefined_filter=None)[源代码][源代码]#
对给定数据应用反向过滤器。
- 参数:
- 数据(M, N) ndarray
输入数据。
- impulse_response : 可调用对象 f(r, c, **filter_params)可调用
滤波器的脉冲响应。参见
LPIFilter2D。这是一个必需的参数,除非提供了 predifined_filter。- filter_paramsdict, 可选
impulse_response 函数的附加关键字参数。
- 最大增益float, 可选
限制滤波器增益。通常,滤波器包含零点,这会导致逆滤波器具有无限增益。高增益会导致伪影的放大,因此建议采用保守的限制。
- 其他参数:
- 预定义过滤器LPIFilter2D,可选
如果你需要在不同的图像上多次应用相同的滤波器,请构造 LPIFilter2D 并在此处指定它。
- skimage.filters.frangi(image, sigmas=range(1, 10, 2), scale_range=None, scale_step=None, alpha=0.5, beta=0.5, gamma=None, black_ridges=True, mode='reflect', cval=0)[源代码][源代码]#
使用Frangi血管滤波器对图像进行滤波。
此过滤器可用于检测连续的山脊,例如血管、皱纹、河流。它可以用于计算整个图像中包含此类对象的比例。
仅针对二维和三维图像定义。计算Hessian矩阵的特征值,以根据[R9152c279884a-1]_中描述的方法计算图像区域与血管的相似性。
- 参数:
- 图像(M, N[, P]) ndarray
包含输入图像数据的数组。
- sigmas浮点数的可迭代对象,可选
作为滤波器尺度的Sigma,即 np.arange(scale_range[0], scale_range[1], scale_step)
- scale_range两个浮点数的2元组,可选
使用的sigma范围。
- scale_stepfloat, 可选
sigma之间的步长。
- alphafloat, 可选
Frangi 修正常数,用于调整滤波器对偏离板状结构的敏感度。
- betafloat, 可选
Frangi 修正常数,用于调整滤波器对偏离类斑点结构敏感度的参数。
- gammafloat, 可选
Frangi 修正常数,用于调整滤波器对高方差/纹理/结构区域的敏感度。默认值为 None,使用 Hessian 范数的最大值的一半。
- black_ridges布尔值,可选
当为 True 时(默认),过滤器检测黑色脊线;当为 False 时,它检测白色脊线。
- 模式{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, 可选
如何处理图像边界外的值。
- cvalfloat, 可选
与模式 ‘constant’ 结合使用时,图像边界外的值。
- 返回:
- 出(M, N[, P]) ndarray
过滤后的图像(所有尺度上的最大像素数)。
注释
此过滤器的早期版本由 Marc Schrijver 实现(2001年11月),D. J. Kroon,特温特大学(2009年5月)[R9152c279884a-2]_,以及 D. G. Ellis(2017年1月)[R9152c279884a-3]_。
参考文献
[1]Frangi, A. F., Niessen, W. J., Vincken, K. L., & Viergever, M. A. (1998,). 多尺度血管增强滤波。在医学图像计算与计算机辅助介入国际会议(第130-137页)。Springer Berlin Heidelberg. DOI:10.1007/BFb0056195
[2]Kroon, D. J.: 基于 Hessian 的 Frangi 血管滤波器。
[3]Ellis, D. G.: ellisdg/frangi3d
- skimage.filters.gabor(image, frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0, mode='reflect', cval=0)[源代码][源代码]#
返回Gabor滤波器的实部和虚部响应。
Gabor滤波器核的实部和虚部应用于图像,响应作为一对数组返回。
Gabor 滤波器是一种线性滤波器,具有由正弦平面波调制的高斯核。Gabor 滤波器的频率和方向表示与人类视觉系统的表示相似。Gabor 滤波器组在计算机视觉和图像处理中常用。它们特别适用于边缘检测和纹理分类。
- 参数:
- 图像二维数组
输入图像。
- 频率浮动
谐波函数的空间频率。以像素为单位指定。
- thetafloat, 可选
以弧度为单位的方位角。如果为0,谐波在x方向上。
- 带宽float, 可选
滤波器捕获的带宽。对于固定带宽,
sigma_x和sigma_y会随着频率的增加而减小。如果sigma_x和sigma_y由用户设置,则忽略此值。- sigma_x, sigma_yfloat, 可选
x 和 y 方向的标准偏差。这些方向适用于 旋转前 的内核。如果 theta = pi/2,那么内核旋转 90 度,因此
sigma_x控制 垂直 方向。- n_stds标量,可选
核的线性大小是 n_stds(默认值为3)个标准差。
- 偏移量float, 可选
谐波函数的相位偏移,单位为弧度。
- 模式{‘constant’, ‘nearest’, ‘reflect’, ‘mirror’, ‘wrap’}, 可选
用于将图像与核进行卷积的模式,传递给 ndi.convolve
- cval标量,可选
如果卷积的
mode是 ‘constant’,则填充输入边缘的值。该参数传递给 ndi.convolve。
- 返回:
- 实部, 虚部数组
使用Gabor滤波器核的实部和虚部进行滤波的图像。图像的尺寸与输入图像相同。
参考文献
示例
>>> from skimage.filters import gabor >>> from skimage import data, io >>> from matplotlib import pyplot as plt
>>> image = data.coins() >>> # detecting edges in a coin image >>> filt_real, filt_imag = gabor(image, frequency=0.6) >>> plt.figure() >>> io.imshow(filt_real) >>> io.show()
>>> # less sensitivity to finer details with the lower frequency kernel >>> filt_real, filt_imag = gabor(image, frequency=0.1) >>> plt.figure() >>> io.imshow(filt_real) >>> io.show()
- skimage.filters.gabor_kernel(frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0, dtype=<class 'numpy.complex128'>)[源代码][源代码]#
返回复杂的二维Gabor滤波器核。
Gabor 核是一个由复数谐波函数调制的高斯核。谐波函数由一个虚数正弦函数和一个实数余弦函数组成。空间频率与谐波的波长和高斯核的标准偏差成反比。带宽也与标准偏差成反比。
- 参数:
- 频率浮动
谐波函数的空间频率。以像素为单位指定。
- thetafloat, 可选
以弧度为单位的方位角。如果为0,谐波在x方向上。
- 带宽float, 可选
滤波器捕获的带宽。对于固定带宽,
sigma_x和sigma_y会随着频率的增加而减小。如果sigma_x和sigma_y由用户设置,则忽略此值。- sigma_x, sigma_yfloat, 可选
x 和 y 方向的标准偏差。这些方向适用于 旋转前 的内核。如果 theta = pi/2,那么内核旋转 90 度,因此
sigma_x控制 垂直 方向。- n_stds标量,可选
核的线性大小是 n_stds(默认值为3)个标准差
- 偏移量float, 可选
谐波函数的相位偏移,单位为弧度。
- dtype{np.complex64, np.complex128}
指定过滤器是单精度还是双精度复数。
- 返回:
- g复杂数组
复杂滤波核。
参考文献
示例
>>> from skimage.filters import gabor_kernel >>> from skimage import io >>> from matplotlib import pyplot as plt
>>> gk = gabor_kernel(frequency=0.2) >>> plt.figure() >>> io.imshow(gk.real) >>> io.show()
>>> # more ripples (equivalent to increasing the size of the >>> # Gaussian spread) >>> gk = gabor_kernel(frequency=0.2, bandwidth=0.1) >>> plt.figure() >>> io.imshow(gk.real) >>> io.show()
- skimage.filters.gaussian(image, sigma=1, output=<DEPRECATED>, mode='nearest', cval=0, preserve_range=False, truncate=4.0, *, channel_axis=None, out=None)[源代码][源代码]#
多维高斯滤波器。
- 参数:
- 图像ndarray
输入图像(灰度或彩色)以进行滤波。
- sigma标量或标量序列,可选
高斯核的标准差。高斯滤波器的标准差按每个轴给定为一个序列,或作为一个单一数字,在这种情况下,它对所有轴都是相等的。
- 模式{‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’},可选
mode参数决定了数组边界的处理方式,其中cval是当 mode 等于 ‘constant’ 时的值。默认值是 ‘nearest’。- cval标量,可选
如果
mode是 ‘constant’,则填充输入边缘之外的值。默认值为 0.0。- preserve_rangebool, 可选
如果为 True,则保留原始值范围。否则,输入的
image将根据img_as_float的约定进行转换(首先根据输入的 dtype 归一化为 [-1.0 ; 1.0] 或 [0 ; 1.0] 的值)更多信息,请参见:https://scikit-image.org/docs/dev/user_guide/data_types.html
- 截断float, 可选
将过滤器截断为此数量的标准差。
- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19: channel_axis 在 0.19 版本中被添加。
- 出ndarray,可选
如果提供,过滤后的图像将存储在此数组中。
Added in version 0.23: out 在 0.23 版本中被添加。
- 返回:
- filtered_imagendarray
过滤后的数组
- 其他参数:
- 输出已弃用
已弃用,改为使用 out。
自 0.23 版本弃用.
注释
这个函数是
scipy.ndimage.gaussian_filter()的包装器。整数数组被转换为浮点数。
out 应该是浮点数数据类型,因为
gaussian将输入的 image 转换为浮点数。如果未提供 out,则会分配并返回另一个数组作为结果。多维滤波器实现为一维卷积滤波器的序列。中间数组以与输出相同的数据类型存储。因此,对于精度有限的输出类型,结果可能不精确,因为中间结果可能以不足的精度存储。
示例
>>> import skimage as ski >>> a = np.zeros((3, 3)) >>> a[1, 1] = 1 >>> a array([[0., 0., 0.], [0., 1., 0.], [0., 0., 0.]]) >>> ski.filters.gaussian(a, sigma=0.4) # mild smoothing array([[0.00163116, 0.03712502, 0.00163116], [0.03712502, 0.84496158, 0.03712502], [0.00163116, 0.03712502, 0.00163116]]) >>> ski.filters.gaussian(a, sigma=1) # more smoothing array([[0.05855018, 0.09653293, 0.05855018], [0.09653293, 0.15915589, 0.09653293], [0.05855018, 0.09653293, 0.05855018]]) >>> # Several modes are possible for handling boundaries >>> ski.filters.gaussian(a, sigma=1, mode='reflect') array([[0.08767308, 0.12075024, 0.08767308], [0.12075024, 0.16630671, 0.12075024], [0.08767308, 0.12075024, 0.08767308]]) >>> # For RGB images, each is filtered separately >>> image = ski.data.astronaut() >>> filtered_img = ski.filters.gaussian(image, sigma=1, channel_axis=-1)
- skimage.filters.hessian(image, sigmas=range(1, 10, 2), scale_range=None, scale_step=None, alpha=0.5, beta=0.5, gamma=15, black_ridges=True, mode='reflect', cval=0)[源代码][源代码]#
使用混合Hessian滤波器对图像进行滤波。
此过滤器可用于检测连续的边缘,例如血管、皱纹、河流。它可以用于计算包含此类对象的整个图像的比例。
仅针对2-D和3-D图像定义。几乎等同于Frangi滤波器,但使用替代的平滑方法。参考 [1] 以了解Frangi和Hessian滤波器之间的差异。
- 参数:
- 图像(M, N[, P]) ndarray
包含输入图像数据的数组。
- sigmas浮点数的可迭代对象,可选
作为滤波器尺度的Sigma,即 np.arange(scale_range[0], scale_range[1], scale_step)
- scale_range两个浮点数的2元组,可选
使用的sigma范围。
- scale_stepfloat, 可选
sigma之间的步长。
- betafloat, 可选
Frangi 修正常数,用于调整滤波器对偏离类斑点结构敏感度的参数。
- gammafloat, 可选
Frangi 修正常数,用于调整滤波器对高方差/纹理/结构区域的敏感度。
- black_ridges布尔值,可选
当为 True 时(默认),过滤器检测黑色脊线;当为 False 时,它检测白色脊线。
- 模式{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, 可选
如何处理图像边界外的值。
- cvalfloat, 可选
与模式 ‘constant’ 结合使用时,图像边界外的值。
- 返回:
- 出(M, N[, P]) ndarray
过滤后的图像(所有尺度上的最大像素数)。
注释
由 Marc Schrijver 撰写 (2001年11月) 由 D. J. Kroon 在特温特大学重写 (2009年5月) [2]
参考文献
[1]Ng, C. C., Yap, M. H., Costen, N., & Li, B. (2014,). 使用混合Hessian滤波器的自动皱纹检测。在亚洲计算机视觉会议上(第609-622页)。Springer国际出版。DOI:10.1007/978-3-319-16811-1_40
[2]Kroon, D. J.: 基于 Hessian 的 Frangi 血管滤波器。
- skimage.filters.laplace(image, ksize=3, mask=None)[源代码][源代码]#
使用拉普拉斯算子找到图像的边缘。
- 参数:
- 图像ndarray
待处理的图像。
- ksizeint, 可选
定义离散拉普拉斯算子的尺寸,使其尺寸为 (ksize,) * image.ndim。
- 掩码ndarray,可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出ndarray
拉普拉斯边缘图。
注释
拉普拉斯算子是通过函数 skimage.restoration.uft.laplacian() 生成的。
- skimage.filters.median(image, footprint=None, out=None, mode='nearest', cval=0.0, behavior='ndimage')[源代码][源代码]#
返回图像的局部中值。
- 参数:
- 图像类似数组
输入图像。
- 足迹ndarray,可选
如果
behavior=='rank',footprint是一个由 1 和 0 组成的二维数组。如果behavior=='ndimage',footprint是一个由 1 和 0 组成的 N 维数组,其维度数量与image相同。如果为 None,footprint将是一个 N 维数组,每个维度有 3 个元素(例如,向量、正方形、立方体等)。- 出ndarray,(与图像相同的 dtype),可选
如果为 None,则分配一个新数组。
- 模式{‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’}, 可选
mode 参数决定了如何处理数组边界,其中
cval是当 mode 等于 ‘constant’ 时的值。默认是 ‘nearest’。Added in version 0.15:
mode在behavior='ndimage'时使用。- cval标量,可选
如果模式为 ‘constant’,则填充输入边缘外的值。默认值为 0.0。
Added in version 0.15:
cval在 0.15 版本中添加,当behavior='ndimage'时使用。- 行为{‘ndimage’, ‘rank’}, 可选
选择使用旧行为(即 < 0.15)还是新行为。旧行为将调用
skimage.filters.rank.median()。新行为将调用scipy.ndimage.median_filter()。默认是 ‘ndimage’。Added in version 0.15:
behavior在 0.15 版本中引入在 0.16 版本发生变更: 默认
behavior已从 ‘rank’ 更改为 ‘ndimage’
- 返回:
- 出2-D 数组 (与输入图像相同的 dtype)
输出图像。
参见
skimage.filters.rank.median基于排序的中值滤波实现,提供更多灵活性,带有额外参数,但专为无符号整数图像设计。
示例
>>> from skimage import data >>> from skimage.morphology import disk >>> from skimage.filters import median >>> img = data.camera() >>> med = median(img, disk(5))
- skimage.filters.meijering(image, sigmas=range(1, 10, 2), alpha=None, black_ridges=True, mode='reflect', cval=0)[源代码][源代码]#
使用 Meijering 神经滤波器过滤图像。
此过滤器可用于检测连续的山脊,例如神经突、皱纹、河流。它可以用于计算包含此类对象的整个图像的比例。
根据 [1] 中描述的方法,计算 Hessian 矩阵的特征值以计算图像区域与神经突的相似性。
- 参数:
- 图像(M, N[, …]) ndarray
包含输入图像数据的数组。
- sigmas浮点数的可迭代对象,可选
作为滤波器尺度的西格玛值
- alphafloat, 可选
形状过滤器常数,选择最大平坦的拉长特征。默认值为 None,选择最优值 -1/(ndim+1)。
- black_ridges布尔值,可选
当为 True 时(默认),过滤器检测黑色脊线;当为 False 时,它检测白色脊线。
- 模式{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, 可选
如何处理图像边界外的值。
- cvalfloat, 可选
与模式 ‘constant’ 结合使用时,图像边界外的值。
- 返回:
- 出(M, N[, …]) ndarray
过滤后的图像(所有尺度上的最大像素数)。
参考文献
[1]Meijering, E., Jacob, M., Sarria, J. C., Steiner, P., Hirling, H., Unser, M. (2004). 设计和验证用于荧光显微镜图像中神经突追踪和分析的工具。细胞计量学A部分, 58(2), 167-176. DOI:10.1002/cyto.a.20022
- skimage.filters.prewitt(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[源代码][源代码]#
使用Prewitt变换找到边缘幅度。
- 参数:
- 图像数组
输入图像。
- 掩码布尔数组,可选
将输出图像裁剪到此掩码。(掩码=0 的值将被设置为 0。)
- 轴int 或 int 序列,可选
计算沿此轴的边缘滤波器。如果未提供,则计算边缘幅度。定义如下:
prw_mag = np.sqrt(sum([prewitt(image, axis=i)**2 for i in range(image.ndim)]) / image.ndim)
如果轴是一个序列,也会计算大小。
- 模式str 或 str 序列,可选
卷积的边界模式。有关模式的描述,请参见
scipy.ndimage.convolve。这可以是单一的边界模式,也可以是每个轴一个边界模式。- cvalfloat, 可选
当 mode 为
'constant'时,这是在图像数据边界之外的值中使用的常数。
- 返回:
- 输出浮点数数组
Prewitt 边缘图。
注释
边缘幅度稍微依赖于边缘方向,因为Prewitt算子对梯度算子的近似并不是完全旋转不变的。为了更好的旋转不变性,应使用Scharr算子。Sobel算子比Prewitt算子有更好的旋转不变性,但比Scharr算子的旋转不变性差。
示例
>>> from skimage import data >>> from skimage import filters >>> camera = data.camera() >>> edges = filters.prewitt(camera)
- skimage.filters.prewitt_h(image, mask=None)[源代码][源代码]#
使用 Prewitt 变换查找图像的水平边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Prewitt 边缘图。
注释
我们使用以下内核:
1/3 1/3 1/3 0 0 0 -1/3 -1/3 -1/3
- skimage.filters.prewitt_v(image, mask=None)[源代码][源代码]#
使用 Prewitt 变换查找图像的垂直边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Prewitt 边缘图。
注释
我们使用以下内核:
1/3 0 -1/3 1/3 0 -1/3 1/3 0 -1/3
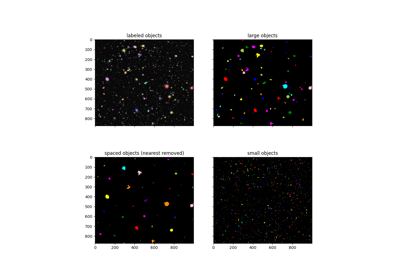
- skimage.filters.rank_order(image)[源代码][源代码]#
返回一个与原图像形状相同的图像,其中每个像素是该像素值在
image唯一值的升序中的索引,即排名顺序值。- 参数:
- 图像ndarray
- 返回:
- 标签无符号整数的 ndarray,形状为 image.shape
新数组,其中每个像素具有
image中相应像素的排序值。像素值介于 0 和 n - 1 之间,其中 n 是image中不同唯一值的数量。此数组的 dtype 将由np.min_scalar_type(image.size)确定。- 原始值一维 ndarray
image的唯一原始值。这将具有与image相同的 dtype。
示例
>>> a = np.array([[1, 4, 5], [4, 4, 1], [5, 1, 1]]) >>> a array([[1, 4, 5], [4, 4, 1], [5, 1, 1]]) >>> rank_order(a) (array([[0, 1, 2], [1, 1, 0], [2, 0, 0]], dtype=uint8), array([1, 4, 5])) >>> b = np.array([-1., 2.5, 3.1, 2.5]) >>> rank_order(b) (array([0, 1, 2, 1], dtype=uint8), array([-1. , 2.5, 3.1]))
- skimage.filters.roberts(image, mask=None)[源代码][源代码]#
使用Roberts交叉算子寻找边缘幅度。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Roberts’ Cross 边缘图。
参见
示例
>>> from skimage import data >>> camera = data.camera() >>> from skimage import filters >>> edges = filters.roberts(camera)
- skimage.filters.roberts_neg_diag(image, mask=None)[源代码][源代码]#
使用Roberts’ Cross算子查找图像的交叉边缘。
内核应用于输入图像,以产生梯度分量在某一方向上的单独测量。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Robert’s 边缘图。
注释
我们使用以下内核:
0 1 -1 0
- skimage.filters.roberts_pos_diag(image, mask=None)[源代码][源代码]#
使用Roberts交叉算子查找图像的交叉边缘。
内核应用于输入图像,以产生梯度分量在某一方向上的单独测量。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Robert’s 边缘图。
注释
我们使用以下内核:
1 0 0 -1
- skimage.filters.sato(image, sigmas=range(1, 10, 2), black_ridges=True, mode='reflect', cval=0)[源代码][源代码]#
使用Sato管状滤波器过滤图像。
此过滤器可用于检测连续的山脊,例如管道、皱纹、河流。它可以用于计算包含此类对象的整个图像的比例。
仅针对二维和三维图像定义。计算Hessian的特征值以根据[R7b0e4f38c6a4-1]_中描述的方法计算图像区域与管道的相似性。
- 参数:
- 图像(M, N[, P]) ndarray
包含输入图像数据的数组。
- sigmas浮点数的可迭代对象,可选
用作滤波器尺度的西格玛。
- black_ridges布尔值,可选
当为 True 时(默认),过滤器检测黑色脊线;当为 False 时,它检测白色脊线。
- 模式{‘constant’, ‘reflect’, ‘wrap’, ‘nearest’, ‘mirror’}, 可选
如何处理图像边界外的值。
- cvalfloat, 可选
与模式 ‘constant’ 结合使用时,图像边界外的值。
- 返回:
- 出(M, N[, P]) ndarray
过滤后的图像(所有尺度上的最大像素数)。
参考文献
[1]Sato, Y., Nakajima, S., Shiraga, N., Atsumi, H., Yoshida, S., Koller, T., …, Kikinis, R. (1998). 医学图像中曲线结构分割与可视化的三维多尺度线滤波器。医学图像分析, 2(2), 143-168. DOI:10.1016/S1361-8415(98)80009-1
- skimage.filters.scharr(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[源代码][源代码]#
使用Scharr变换查找边缘幅度。
- 参数:
- 图像数组
输入图像。
- 掩码布尔数组,可选
将输出图像裁剪到此掩码。(掩码=0 的值将被设置为 0。)
- 轴int 或 int 序列,可选
计算沿此轴的边缘滤波器。如果未提供,则计算边缘幅度。定义如下:
sch_mag = np.sqrt(sum([scharr(image, axis=i)**2 for i in range(image.ndim)]) / image.ndim)
如果轴是一个序列,也会计算大小。
- 模式str 或 str 序列,可选
卷积的边界模式。有关模式的描述,请参见
scipy.ndimage.convolve。这可以是单一的边界模式,也可以是每个轴一个边界模式。- cvalfloat, 可选
当 mode 为
'constant'时,这是在图像数据边界之外的值中使用的常数。
- 返回:
- 输出浮点数数组
Scharr 边缘图。
注释
Scharr 算子比其他边缘滤波器(如 Sobel 或 Prewitt 算子)具有更好的旋转不变性。
参考文献
[1]D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives.
示例
>>> from skimage import data >>> from skimage import filters >>> camera = data.camera() >>> edges = filters.scharr(camera)
- skimage.filters.scharr_h(image, mask=None)[源代码][源代码]#
使用 Scharr 变换查找图像的水平边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Scharr 边缘图。
注释
我们使用以下内核:
3 10 3 0 0 0 -3 -10 -3
参考文献
[1]D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives.
- skimage.filters.scharr_v(image, mask=None)[源代码][源代码]#
使用 Scharr 变换查找图像的垂直边缘。
- 参数:
- 图像二维数组
待处理的图像
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Scharr 边缘图。
注释
我们使用以下内核:
3 0 -3 10 0 -10 3 0 -3
参考文献
[1]D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives.
- skimage.filters.sobel(image, mask=None, *, axis=None, mode='reflect', cval=0.0)[源代码][源代码]#
使用Sobel滤波器在图像中寻找边缘。
- 参数:
- 图像数组
输入图像。
- 掩码布尔数组,可选
将输出图像裁剪到此掩码。(掩码=0 的值将被设置为 0。)
- 轴int 或 int 序列,可选
计算沿此轴的边缘滤波器。如果未提供,则计算边缘幅度。定义如下:
sobel_mag = np.sqrt(sum([sobel(image, axis=i)**2 for i in range(image.ndim)]) / image.ndim)
如果轴是一个序列,也会计算大小。
- 模式str 或 str 序列,可选
卷积的边界模式。有关模式的描述,请参见
scipy.ndimage.convolve。这可以是单一的边界模式,也可以是每个轴一个边界模式。- cvalfloat, 可选
当 mode 为
'constant'时,这是在图像数据边界之外的值中使用的常数。
- 返回:
- 输出浮点数数组
Sobel 边缘图。
参考文献
[1]D. Kroon, 2009, Short Paper University Twente, Numerical Optimization of Kernel Based Image Derivatives.
示例
>>> from skimage import data >>> from skimage import filters >>> camera = data.camera() >>> edges = filters.sobel(camera)
- skimage.filters.sobel_h(image, mask=None)[源代码][源代码]#
使用 Sobel 变换找到图像的水平边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Sobel 边缘图。
注释
我们使用以下内核:
1 2 1 0 0 0 -1 -2 -1
- skimage.filters.sobel_v(image, mask=None)[源代码][源代码]#
使用Sobel变换查找图像的垂直边缘。
- 参数:
- 图像二维数组
待处理的图像。
- 掩码2-D 数组, 可选
一个可选的掩码,用于将应用限制在特定区域。请注意,掩码区域周围的像素也会被掩码,以防止掩码区域影响结果。
- 返回:
- 输出二维数组
Sobel 边缘图。
注释
我们使用以下内核:
1 0 -1 2 0 -2 1 0 -1
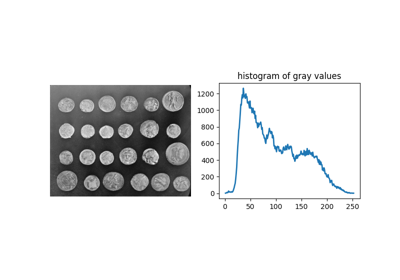
- skimage.filters.threshold_isodata(image=None, nbins=256, return_all=False, *, hist=None)[源代码][源代码]#
基于ISODATA方法返回阈值。
基于直方图的阈值,称为 Ridler-Calvard 方法或中间均值法。返回的阈值满足以下等式:
threshold = (image[image <= threshold].mean() + image[image > threshold].mean()) / 2.0
也就是说,返回的阈值是强度,它将图像分成两组像素,其中阈值强度位于这两组像素的平均强度之间。
对于整数图像,上述等式在1以内成立;对于浮点图像,等式在直方图的区间宽度内成立。
必须提供图像或直方图。如果提供了直方图,则忽略图像的实际直方图。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- nbinsint, 可选
用于计算直方图的箱数。此值对整数数组忽略。
- return_allbool, 可选
如果为 False(默认),则仅返回满足上述等式的最低阈值。如果为 True,则返回所有有效阈值。
- hist数组,或两个数组的 2-tuple,可选
直方图以确定阈值,并附带一个对应于箱中心强度的数组。或者,仅传递直方图。
- 返回:
- 阈值浮点数或整数或数组
阈值。
参考文献
[1]Ridler, TW & Calvard, S (1978), “使用迭代选择方法的图像阈值处理” IEEE Transactions on Systems, Man and Cybernetics 8: 630-632, DOI:10.1109/TSMC.1978.4310039
[2]Sezgin M. 和 Sankur B. (2004) “图像阈值技术及其定量性能评估调查” 电子成像杂志, 13(1): 146-165, http://www.busim.ee.boun.edu.tr/~sankur/SankurFolder/Threshold_survey.pdf DOI:10.1117/1.1631315
[3]ImageJ AutoThresholder 代码, http://fiji.sc/wiki/index.php/Auto_Threshold
示例
>>> from skimage.data import coins >>> image = coins() >>> thresh = threshold_isodata(image) >>> binary = image > thresh
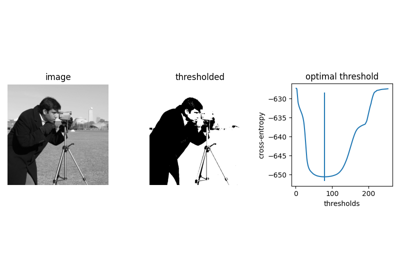
- skimage.filters.threshold_li(image, *, tolerance=None, initial_guess=None, iter_callback=None)[源代码][源代码]#
通过Li的迭代最小交叉熵方法计算阈值。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- 容差float, 可选
当迭代中阈值的变化小于此值时,完成计算。默认情况下,这是
image中强度值之间最小差异的一半。- 初始猜测浮点数或可调用对象[[数组[浮点数]], 浮点数], 可选
Li的迭代方法使用梯度下降来找到最优阈值。如果图像强度直方图包含超过两个模式(峰值),梯度下降可能会陷入局部最优。迭代的一个初始猜测可以帮助算法找到全局最优阈值。浮点值定义了一个特定的起点,而可调用对象应该接受一个图像强度数组并返回一个浮点值。有效的可调用对象示例包括``numpy.mean``(默认)、
lambda arr: numpy.quantile(arr, 0.95),甚至是skimage.filters.threshold_otsu()。- iter_callbackCallable[[float], Any], 可选
一个在算法每次迭代时将在阈值处调用的函数。
- 返回:
- 阈值浮动
上限阈值。所有强度高于此值的像素都被认为是前景。
参考文献
[1]Li C.H. 和 Lee C.K. (1993) “最小交叉熵阈值法” 模式识别, 26(4): 617-625 DOI:10.1016/0031-3203(93)90115-D
[2]Li C.H. 和 Tam P.K.S. (1998) “一种用于最小交叉熵阈值的迭代算法” 模式识别通讯, 18(8): 771-776 DOI:10.1016/S0167-8655(98)00057-9
[3]Sezgin M. 和 Sankur B. (2004) “图像阈值技术及其定量性能评估调查” 电子成像杂志, 13(1): 146-165 DOI:10.1117/1.1631315
[4]ImageJ AutoThresholder 代码, http://fiji.sc/wiki/index.php/Auto_Threshold
示例
>>> from skimage.data import camera >>> image = camera() >>> thresh = threshold_li(image) >>> binary = image > thresh
- skimage.filters.threshold_local(image, block_size=3, method='gaussian', offset=0, mode='reflect', param=None, cval=0)[源代码][源代码]#
基于局部像素邻域计算一个阈值掩码图像。
也称为自适应或动态阈值。阈值是像素局部邻域的加权平均值减去一个常数。或者,可以使用“通用”方法通过给定函数动态确定阈值。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- block_size整数或整数序列
用于计算阈值的像素邻域的奇数大小(例如 3, 5, 7, …, 21, …)。
- 方法{‘generic’, ‘gaussian’, ‘mean’, ‘median’}, 可选
用于确定加权平均图像中局部邻域自适应阈值的方法。
‘generic’: 使用自定义函数(参见
param参数)‘gaussian’: 应用高斯滤波器(参见
param参数以自定义 sigma 值)‘mean’: 应用算术平均滤波器
‘中位数’: 应用中位数排名过滤器
默认情况下,使用 ‘gaussian’ 方法。
- 偏移量float, 可选
从邻域的加权平均值中减去的常数,用于计算局部阈值。默认偏移量为0。
- 模式{‘reflect’, ‘constant’, ‘nearest’, ‘mirror’, ‘wrap’},可选
mode 参数决定了如何处理数组边界,当 mode 等于 ‘constant’ 时,cval 是该值。默认是 ‘reflect’。
- 参数{int, function}, 可选
对于’gaussian’方法指定sigma,或者对于’generic’方法指定函数对象。此函数接受局部邻域的扁平数组作为单个参数,并返回中心像素的计算阈值。
- cvalfloat, 可选
如果模式是 ‘constant’,则填充输入边缘之外的值。
- 返回:
- 阈值(M, N[, …]) ndarray
阈值图像。输入图像中所有高于阈值图像中对应像素的像素被视为前景。
参考文献
[1]Gonzalez, R. C. 和 Wood, R. E. 《数字图像处理(第二版)》。Prentice-Hall Inc., 2002: 600–612. ISBN: 0-201-18075-8
示例
>>> from skimage.data import camera >>> image = camera()[:50, :50] >>> binary_image1 = image > threshold_local(image, 15, 'mean') >>> func = lambda arr: arr.mean() >>> binary_image2 = image > threshold_local(image, 15, 'generic', ... param=func)
- skimage.filters.threshold_mean(image)[源代码][源代码]#
基于灰度值的平均值返回阈值。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- 返回:
- 阈值浮动
上限阈值。所有强度高于此值的像素都被认为是前景。
参考文献
[1]C. A. Glasbey, “An analysis of histogram-based thresholding algorithms,” CVGIP: Graphical Models and Image Processing, vol. 55, pp. 532-537, 1993. DOI:10.1006/cgip.1993.1040
示例
>>> from skimage.data import camera >>> image = camera() >>> thresh = threshold_mean(image) >>> binary = image > thresh
- skimage.filters.threshold_minimum(image=None, nbins=256, max_num_iter=10000, *, hist=None)[源代码][源代码]#
基于最小方法返回阈值。
如果没有提供直方图,则计算输入
image的直方图,并进行平滑处理,直到只剩下两个最大值。然后,两者之间的最小值即为阈值。必须提供图像或直方图。如果提供了直方图,则忽略图像的实际直方图。
- 参数:
- 图像(M, N[, …]) ndarray, 可选
灰度输入图像。
- nbinsint, 可选
用于计算直方图的箱数。此值对整数数组忽略。
- max_num_iterint, 可选
平滑直方图的最大迭代次数。
- hist数组,或两个数组的 2-tuple,可选
直方图以确定阈值,并附带一个对应于箱中心强度的数组。或者,仅传递直方图。
- 返回:
- 阈值浮动
上限阈值。所有强度高于此值的像素都被认为是前景。
- Raises:
- RuntimeError
如果在直方图中无法找到两个局部最大值,或者如果平滑操作超过1e4次迭代。
参考文献
[1]C. A. Glasbey, “An analysis of histogram-based thresholding algorithms,” CVGIP: Graphical Models and Image Processing, vol. 55, pp. 532-537, 1993.
[2]Prewitt, JMS & Mendelsohn, ML (1966), “细胞图像的分析”, 纽约科学院年鉴 128: 1035-1053 DOI:10.1111/j.1749-6632.1965.tb11715.x
示例
>>> from skimage.data import camera >>> image = camera() >>> thresh = threshold_minimum(image) >>> binary = image > thresh
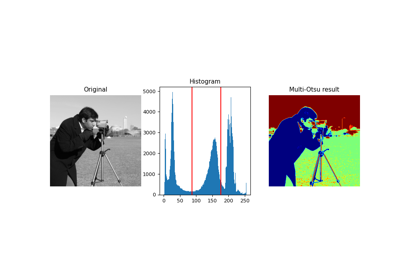
- skimage.filters.threshold_multiotsu(image=None, classes=3, nbins=256, *, hist=None)[源代码][源代码]#
生成 classes-1 个阈值,以根据 Otsu 的多类方法分割 图像 中的灰度级。
阈值的选择是为了最大化阈值化灰度级类别之间的成对方差总和。更多详情请参见注释和 [1]。
必须提供图像或直方图。如果提供了直方图,则忽略图像的实际直方图。
- 参数:
- 图像(M, N[, …]) ndarray, 可选
灰度输入图像。
- 类int, 可选
要进行阈值处理的类的数量,即生成的区域数量。
- nbinsint, 可选
用于计算直方图的箱数。此值对整数数组无效。
- hist数组,或两个数组的 2-tuple,可选
用于确定阈值的直方图,以及可选的相应箱中心强度数组。如果没有提供直方图,此函数将从图像中计算它(参见注释)。
- 返回:
- thresh数组
包含所需类别的阈值的数组。
- Raises:
- ValueError
如果
image包含的灰度值少于所需类别的数量。
注释
此实现依赖于一个Cython函数,其复杂度为 \(O\left(\frac{Ch^{C-1}}{(C-1)!}\right)\),其中 \(h\) 是直方图的箱数,\(C\) 是所需类别的数量。
如果没有提供直方图,此函数将使用
skimage.exposure.histogram,其行为与 np.histogram 不同。虽然两者都允许使用,但为了行为一致,建议使用前者。输入图像必须是灰度图像。
参考文献
[1]Liao, P-S., Chen, T-S. 和 Chung, P-C., “多级阈值的快速算法”, 信息科学与工程杂志 17 (5): 713-727, 2001. 可从以下网址获取: <https://ftp.iis.sinica.edu.tw/JISE/2001/200109_01.pdf> DOI:10.6688/JISE.2001.17.5.1
[2]Tosa, Y., “多重Otsu阈值”,一个用于ImageJ的Java插件。可从以下网址获取:<http://imagej.net/plugins/download/Multi_OtsuThreshold.java>
示例
>>> from skimage.color import label2rgb >>> from skimage import data >>> image = data.camera() >>> thresholds = threshold_multiotsu(image) >>> regions = np.digitize(image, bins=thresholds) >>> regions_colorized = label2rgb(regions)
- skimage.filters.threshold_niblack(image, window_size=15, k=0.2)[源代码][源代码]#
对数组应用Niblack局部阈值。
使用以下公式为图像中的每个像素计算一个阈值 T:
T = m(x,y) - k * s(x,y)
其中 m(x,y) 和 s(x,y) 分别是像素 (x,y) 邻域的均值和标准差,该邻域由以像素为中心的 w 乘 w 大小的矩形窗口定义。k 是一个可配置的参数,用于权衡标准差的影响。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- 窗口大小int,或 int 的可迭代对象,可选
窗口大小指定为一个单独的奇数整数(3, 5, 7, …),或一个长度为
image.ndim的可迭代对象,其中仅包含奇数整数(例如(1, 5, 5))。- kfloat, 可选
阈值公式中参数 k 的值。
- 返回:
- 阈值(M, N[, …]) ndarray
阈值掩码。所有强度高于此值的像素都被认为是前景。
注释
该算法最初是为文本识别设计的。
Bradley 阈值是 Niblack 阈值的一个特例,两者是等价的。
>>> from skimage import data >>> image = data.page() >>> q = 1 >>> threshold_image = threshold_niblack(image, k=0) * q
对于某个值
q。默认情况下,Bradley 和 Roth 使用q=1。参考文献
[1]W. Niblack, An introduction to Digital Image Processing, Prentice-Hall, 1986.
[2]D. Bradley and G. Roth, “Adaptive thresholding using Integral Image”, Journal of Graphics Tools 12(2), pp. 13-21, 2007. DOI:10.1080/2151237X.2007.10129236
示例
>>> from skimage import data >>> image = data.page() >>> threshold_image = threshold_niblack(image, window_size=7, k=0.1)
- skimage.filters.threshold_otsu(image=None, nbins=256, *, hist=None)[源代码][源代码]#
基于大津法返回阈值。
必须提供图像或直方图。如果提供了直方图,则忽略图像的实际直方图。
- 参数:
- 图像(M, N[, …]) ndarray, 可选
灰度输入图像。
- nbinsint, 可选
用于计算直方图的箱数。此值对整数数组忽略。
- hist数组,或两个数组的 2-tuple,可选
用于确定阈值的直方图,以及可选的相应箱中心强度数组。如果没有提供直方图,此函数将从图像中计算它。
- 返回:
- 阈值浮动
上限阈值。所有强度高于此值的像素都被认为是前景。
注释
输入图像必须是灰度图像。
参考文献
示例
>>> from skimage.data import camera >>> image = camera() >>> thresh = threshold_otsu(image) >>> binary = image <= thresh
- skimage.filters.threshold_sauvola(image, window_size=15, k=0.2, r=None)[源代码][源代码]#
对数组应用 Sauvola 局部阈值。Sauvola 是 Niblack 技术的改进版。
在原始方法中,使用以下公式为图像中的每个像素计算一个阈值 T:
T = m(x,y) * (1 + k * ((s(x,y) / R) - 1))
其中 m(x,y) 和 s(x,y) 是像素 (x,y) 邻域的均值和标准差,该邻域由一个大小为 w 乘 w 的矩形窗口定义,窗口中心为该像素。k 是一个可配置的参数,用于加权标准差的影响。R 是灰度图像的最大标准差。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- 窗口大小int,或 int 的可迭代对象,可选
窗口大小指定为一个单独的奇数整数(3, 5, 7, …),或一个长度为
image.ndim的可迭代对象,其中仅包含奇数整数(例如(1, 5, 5))。- kfloat, 可选
正参数 k 的值。
- rfloat, 可选
R 的值,即标准差的动态范围。如果为 None,则设置为图像数据类型范围的一半。
- 返回:
- 阈值(M, N[, …]) ndarray
阈值掩码。所有强度高于此值的像素都被认为是前景。
注释
该算法最初是为文本识别设计的。
参考文献
[1]J. Sauvola and M. Pietikainen, “Adaptive document image binarization,” Pattern Recognition 33(2), pp. 225-236, 2000. DOI:10.1016/S0031-3203(99)00055-2
示例
>>> from skimage import data >>> image = data.page() >>> t_sauvola = threshold_sauvola(image, window_size=15, k=0.2) >>> binary_image = image > t_sauvola
- skimage.filters.threshold_triangle(image, nbins=256)[源代码][源代码]#
基于三角算法返回阈值。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- nbinsint, 可选
用于计算直方图的箱数。此值对整数数组忽略。
- 返回:
- 阈值浮动
上限阈值。所有强度高于此值的像素都被认为是前景。
参考文献
[1]Zack, G. W., Rogers, W. E. 和 Latt, S. A., 1977, 姐妹染色单体交换频率的自动测量, 组织化学与细胞化学杂志 25 (7), pp. 741-753 DOI:10.1177/25.7.70454
[2]ImageJ AutoThresholder 代码, http://fiji.sc/wiki/index.php/Auto_Threshold
示例
>>> from skimage.data import camera >>> image = camera() >>> thresh = threshold_triangle(image) >>> binary = image > thresh
- skimage.filters.threshold_yen(image=None, nbins=256, *, hist=None)[源代码][源代码]#
基于Yen方法返回阈值。必须提供图像或直方图。如果提供了直方图,则忽略图像的实际直方图。
- 参数:
- 图像(M, N[, …]) ndarray
灰度输入图像。
- nbinsint, 可选
用于计算直方图的箱数。此值对整数数组忽略。
- hist数组,或两个数组的 2-tuple,可选
用于确定阈值的直方图,以及可选的对应箱中心强度数组。此函数的另一种用法是仅传递 hist。
- 返回:
- 阈值浮动
上限阈值。所有强度高于此值的像素都被认为是前景。
参考文献
[1]Yen J.C., Chang F.J., and Chang S. (1995) “一种新的自动多级阈值选择准则” IEEE 图像处理汇刊, 4(3): 370-378. DOI:10.1109/83.366472
[2]Sezgin M. 和 Sankur B. (2004) “图像阈值技术及其定量性能评估调查” 《电子成像杂志》, 13(1): 146-165, DOI:10.1117/1.1631315 http://www.busim.ee.boun.edu.tr/~sankur/SankurFolder/Threshold_survey.pdf
[3]ImageJ AutoThresholder 代码, http://fiji.sc/wiki/index.php/Auto_Threshold
示例
>>> from skimage.data import camera >>> image = camera() >>> thresh = threshold_yen(image) >>> binary = image <= thresh
- skimage.filters.try_all_threshold(image, figsize=(8, 5), verbose=True)[源代码][源代码]#
返回一个比较不同阈值方法输出的图形。
- 参数:
- 图像(M, N) ndarray
输入图像。
- figsizetuple, 可选
图表尺寸(以英寸为单位)。
- 详细bool, 可选
为每个方法打印函数名称。
- 返回:
- fig, ax元组
Matplotlib 图形和坐标轴。
注释
使用了以下算法:
isodata
li
平均
最小值
otsu
三角形
日元
示例
>>> from skimage.data import text >>> fig, ax = try_all_threshold(text(), figsize=(10, 6), verbose=False)
- skimage.filters.unsharp_mask(image, radius=1.0, amount=1.0, preserve_range=False, *, channel_axis=None)[源代码][源代码]#
非锐化掩模滤镜。
锐化细节被识别为原始图像与其模糊版本之间的差异。这些细节随后被缩放,并添加回原始图像。
- 参数:
- 图像(M[, …][, C]) ndarray
输入图像。
- 半径标量或标量序列,可选
如果给定一个标量,那么它的值将用于所有维度。如果给定一个序列,那么除了多通道图像的最后一个维度外,每个维度必须恰好有一个半径。请注意,0 半径意味着没有模糊处理,负值是不允许的。
- 金额标量,可选
细节将通过这个因子放大。因子可以是0或负数。通常,它是一个小的正数,例如1.0。
- preserve_rangebool, 可选
是否保留原始值范围。否则,输入图像将根据
img_as_float的约定进行转换。另见 https://scikit-image.org/docs/dev/user_guide/data_types.html- channel_axisint 或 None, 可选
如果为 None,则假定图像是灰度图像(单通道)。否则,此参数指示数组的哪个轴对应于通道。
Added in version 0.19:
channel_axis在 0.19 版本中被添加。
- 返回:
- 输出(M[, …][, C]) 浮点型 ndarray
应用了钝化蒙版的图像。
注释
非锐化掩模是一种图像锐化技术。它是一种线性图像操作,并且在数值上是稳定的,不像反卷积那样是一个不适定问题。由于这种稳定性,它通常比反卷积更受欢迎。
主要思想如下:锐利细节被识别为原始图像与其模糊版本之间的差异。这些细节在缩放步骤之后被加回到原始图像中:
增强图像 = 原始图像 + 数量 * (原始图像 - 模糊图像)
当独立地将此滤镜应用于多个颜色层时,可能会发生颜色渗出。通过在适当的颜色空间(如HSV、HSL、YUV或YCbCr)中仅处理亮度/亮度/强度通道,可以获得更令人愉悦的视觉效果。
模糊蒙版在大多数数字图像处理入门书籍中都有描述。此实现基于 [1]。
参考文献
[1]Maria Petrou, Costas Petrou 《图像处理:基础》,(2010),第二版,第357页,ISBN 13: 9781119994398 DOI:10.1002/9781119994398
[2]Wikipedia. 非锐化掩模 https://en.wikipedia.org/wiki/Unsharp_masking
示例
>>> array = np.ones(shape=(5,5), dtype=np.uint8)*100 >>> array[2,2] = 120 >>> array array([[100, 100, 100, 100, 100], [100, 100, 100, 100, 100], [100, 100, 120, 100, 100], [100, 100, 100, 100, 100], [100, 100, 100, 100, 100]], dtype=uint8) >>> np.around(unsharp_mask(array, radius=0.5, amount=2),2) array([[0.39, 0.39, 0.39, 0.39, 0.39], [0.39, 0.39, 0.38, 0.39, 0.39], [0.39, 0.38, 0.53, 0.38, 0.39], [0.39, 0.39, 0.38, 0.39, 0.39], [0.39, 0.39, 0.39, 0.39, 0.39]])
>>> array = np.ones(shape=(5,5), dtype=np.int8)*100 >>> array[2,2] = 127 >>> np.around(unsharp_mask(array, radius=0.5, amount=2),2) array([[0.79, 0.79, 0.79, 0.79, 0.79], [0.79, 0.78, 0.75, 0.78, 0.79], [0.79, 0.75, 1. , 0.75, 0.79], [0.79, 0.78, 0.75, 0.78, 0.79], [0.79, 0.79, 0.79, 0.79, 0.79]])
>>> np.around(unsharp_mask(array, radius=0.5, amount=2, preserve_range=True), 2) array([[100. , 100. , 99.99, 100. , 100. ], [100. , 99.39, 95.48, 99.39, 100. ], [ 99.99, 95.48, 147.59, 95.48, 99.99], [100. , 99.39, 95.48, 99.39, 100. ], [100. , 100. , 99.99, 100. , 100. ]])
- skimage.filters.wiener(data, impulse_response=None, filter_params=None, K=0.25, predefined_filter=None)[源代码][源代码]#
最小均方误差(维纳)逆滤波器。
- 参数:
- 数据(M, N) ndarray
输入数据。
- K浮点数或 (M, N) 的 ndarray
噪声功率谱与未退化图像的功率谱之比。
- impulse_response : 可调用对象 f(r, c, **filter_params)可调用
滤波器的脉冲响应。参见 LPIFilter2D.__init__。
- filter_paramsdict, 可选
impulse_response 函数的附加关键字参数。
- 其他参数:
- 预定义过滤器LPIFilter2D
如果你需要在不同的图像上多次应用相同的滤波器,请构造 LPIFilter2D 并在此处指定它。
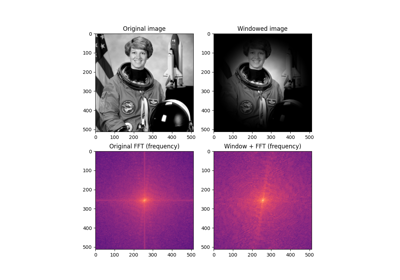
- skimage.filters.window(window_type, shape, warp_kwargs=None)[源代码][源代码]#
返回一个给定大小和维度的n维窗口。
- 参数:
- 窗口类型字符串, 浮点数, 或 元组
要创建的窗口类型。这里允许使用
scipy.signal.get_window支持的任何窗口类型。请参阅下面的当前列表,或您机器上 SciPy 版本的 SciPy 文档。- 形状整数元组或整数
窗口沿每个轴的形状。如果提供了一个整数,则生成一个1D窗口。
- warp_kwargsdict
传递给
skimage.transform.warp的关键字参数(例如,warp_kwargs={'order':3}以更改插值方法)。
- 返回:
- nd_windowndarray
指定
shape的窗口。dtype为np.float64。
注释
此函数基于
scipy.signal.get_window,因此可以访问该函数可用的所有窗口类型(例如,"hann","boxcar")。请注意,某些窗口类型需要参数,这些参数必须与窗口名称一起作为元组提供(例如,("tukey", 0.8))。如果仅提供一个浮点数,则将其解释为Kaiser窗口的beta参数。更多详情请参见 https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.windows.get_window.html。
请注意,此函数生成一个指定
shape的双精度数组,因此可以生成占用大量可用内存的非常大的数组。这里创建nD窗口的方法是首先计算从目标nD窗口中心到数组中每个位置的欧几里得距离。该距离用于从``scipy.signal.get_window``返回的1D窗口中进行采样,并进行插值。插值方法可以通过传递给`skimage.transform.warp`的``order``关键字参数来更改。
输出窗口中的一些坐标将超出原始信号的范围;这些部分将用零填充。
窗口类型: - boxcar - triang - blackman - hamming - hann - bartlett - flattop - parzen - bohman - blackmanharris - nuttall - barthann - kaiser (需要 beta) - gaussian (需要标准差) - general_gaussian (需要功率, 宽度) - slepian (需要宽度) - dpss (需要归一化半带宽) - chebwin (需要衰减) - exponential (需要衰减尺度) - tukey (需要渐变部分)
参考文献
[1]二维窗口设计, 维基百科, https://en.wikipedia.org/wiki/Two_dimensional_window_design
示例
返回一个形状为 (512, 512) 的汉宁窗:
>>> from skimage.filters import window >>> w = window('hann', (512, 512))
返回一个beta参数为16且形状为(256, 256, 35)的Kaiser窗口:
>>> w = window(16, (256, 256, 35))
返回一个 alpha 参数为 0.8 且形状为 (100, 300) 的 Tukey 窗口:
>>> w = window(('tukey', 0.8), (100, 300))
- class skimage.filters.LPIFilter2D(impulse_response, **filter_params)[源代码][源代码]#
基类:
object线性位置不变滤波器(二维)
- __init__(impulse_response, **filter_params)[源代码][源代码]#
- 参数:
- impulse_response : 可调用对象 f(r, c, **filter_params)可调用
生成脉冲响应的函数。
r和c是表示行和列位置的一维向量,换句话说,坐标是 (r[0],c[0]),(r[0],c[1]) 等。**filter_params 被传递。换句话说,
impulse_response可以这样调用:>>> def impulse_response(r, c, **filter_params): ... pass >>> >>> r = [0,0,0,1,1,1,2,2,2] >>> c = [0,1,2,0,1,2,0,1,2] >>> filter_params = {'kw1': 1, 'kw2': 2, 'kw3': 3} >>> impulse_response(r, c, **filter_params)
示例
未归一化系数的Gaussian滤波器:
>>> def filt_func(r, c, sigma=1): ... return np.exp(-(r**2 + c**2)/(2 * sigma**2)) >>> filter = LPIFilter2D(filt_func)