备注
转到结尾 下载完整示例代码。或在浏览器中通过 Binder 运行此示例。
Li 阈值化#
1993年,Li和Lee提出了一种寻找图像“最优”阈值的新标准,以区分背景和前景 [1]。他们提出,最小化前景与前景均值之间以及背景与背景均值之间的*交叉熵*,在大多数情况下会给出最佳阈值。
直到1998年,找到这个阈值的方法是通过尝试所有可能的阈值,然后选择具有最小交叉熵的那个。在那时,Li和Tam实现了一种新的迭代方法,通过使用交叉熵的斜率来更快地找到最佳点 [2]。这是scikit-image的 skimage.filters.threshold_li() 中实现的方法。
在这里,我们通过Li的迭代方法展示了交叉熵及其优化。请注意,我们使用的是私有函数 _cross_entropy,在生产代码中不应使用,因为它可能会发生变化。
import numpy as np
import matplotlib.pyplot as plt
from skimage import data
from skimage import filters
from skimage.filters.thresholding import _cross_entropy
cell = data.cell()
camera = data.camera()
首先,我们绘制 skimage.data.camera() 图像在所有可能阈值下的交叉熵。
thresholds = np.arange(np.min(camera) + 1.5, np.max(camera) - 1.5)
entropies = [_cross_entropy(camera, t) for t in thresholds]
optimal_camera_threshold = thresholds[np.argmin(entropies)]
fig, ax = plt.subplots(1, 3, figsize=(8, 3))
ax[0].imshow(camera, cmap='gray')
ax[0].set_title('image')
ax[0].set_axis_off()
ax[1].imshow(camera > optimal_camera_threshold, cmap='gray')
ax[1].set_title('thresholded')
ax[1].set_axis_off()
ax[2].plot(thresholds, entropies)
ax[2].set_xlabel('thresholds')
ax[2].set_ylabel('cross-entropy')
ax[2].vlines(
optimal_camera_threshold,
ymin=np.min(entropies) - 0.05 * np.ptp(entropies),
ymax=np.max(entropies) - 0.05 * np.ptp(entropies),
)
ax[2].set_title('optimal threshold')
fig.tight_layout()
print('The brute force optimal threshold is:', optimal_camera_threshold)
print('The computed optimal threshold is:', filters.threshold_li(camera))
plt.show()
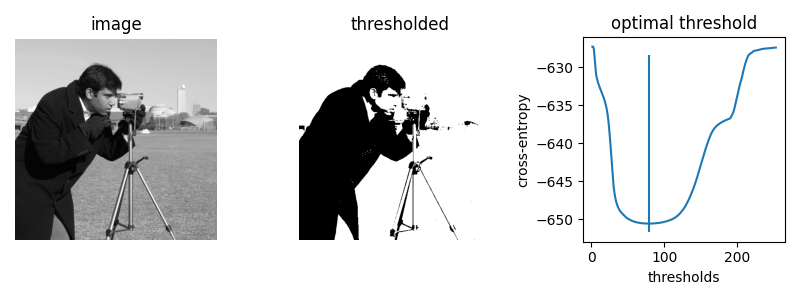
The brute force optimal threshold is: 78.5
The computed optimal threshold is: 78.91288426606151
接下来,我们使用 threshold_li 的 iter_callback 功能来实时检查优化过程。
iter_thresholds = []
optimal_threshold = filters.threshold_li(camera, iter_callback=iter_thresholds.append)
iter_entropies = [_cross_entropy(camera, t) for t in iter_thresholds]
print('Only', len(iter_thresholds), 'thresholds examined.')
fig, ax = plt.subplots()
ax.plot(thresholds, entropies, label='all threshold entropies')
ax.plot(iter_thresholds, iter_entropies, label='optimization path')
ax.scatter(iter_thresholds, iter_entropies, c='C1')
ax.legend(loc='upper right')
plt.show()
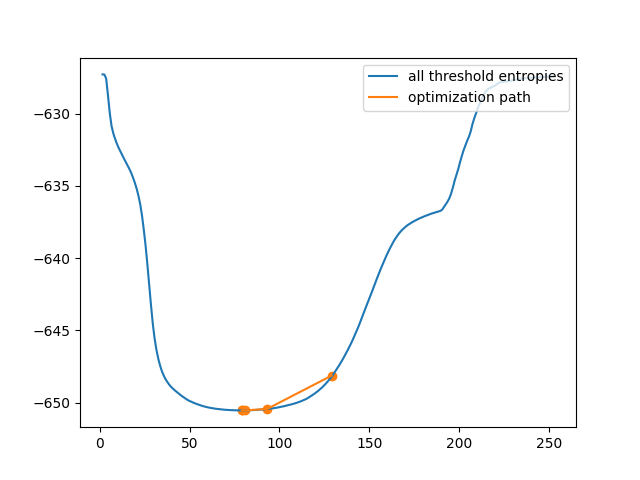
Only 5 thresholds examined.
这显然比暴力方法要高效得多。然而,在某些图像中,交叉熵不是 凸 的,这意味着只有一个最优解。在这种情况下,梯度下降可能会产生一个非最优的阈值。在这个例子中,我们可以看到,优化初始猜测不佳会导致阈值选择不佳。
iter_thresholds2 = []
opt_threshold2 = filters.threshold_li(
cell, initial_guess=64, iter_callback=iter_thresholds2.append
)
thresholds2 = np.arange(np.min(cell) + 1.5, np.max(cell) - 1.5)
entropies2 = [_cross_entropy(cell, t) for t in thresholds]
iter_entropies2 = [_cross_entropy(cell, t) for t in iter_thresholds2]
fig, ax = plt.subplots(1, 3, figsize=(8, 3))
ax[0].imshow(cell, cmap='magma')
ax[0].set_title('image')
ax[0].set_axis_off()
ax[1].imshow(cell > opt_threshold2, cmap='gray')
ax[1].set_title('thresholded')
ax[1].set_axis_off()
ax[2].plot(thresholds2, entropies2, label='all threshold entropies')
ax[2].plot(iter_thresholds2, iter_entropies2, label='optimization path')
ax[2].scatter(iter_thresholds2, iter_entropies2, c='C1')
ax[2].legend(loc='upper right')
plt.show()
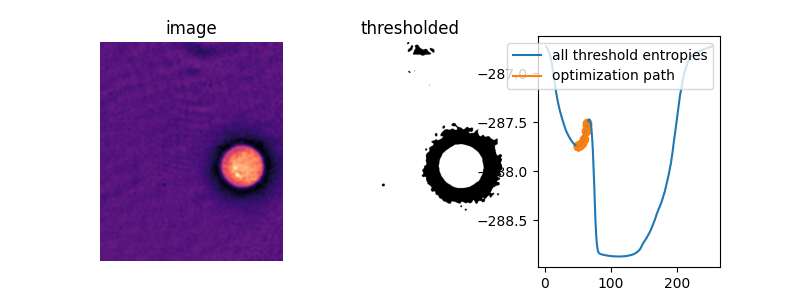
在这张图中,令人惊讶的是,默认 初始猜测,即图像的平均值,实际上 正好 位于目标函数两个“谷”之间的峰值上。如果不提供初始猜测,Li的阈值方法根本不起作用!
iter_thresholds3 = []
opt_threshold3 = filters.threshold_li(cell, iter_callback=iter_thresholds3.append)
iter_entropies3 = [_cross_entropy(cell, t) for t in iter_thresholds3]
fig, ax = plt.subplots(1, 3, figsize=(8, 3))
ax[0].imshow(cell, cmap='magma')
ax[0].set_title('image')
ax[0].set_axis_off()
ax[1].imshow(cell > opt_threshold3, cmap='gray')
ax[1].set_title('thresholded')
ax[1].set_axis_off()
ax[2].plot(thresholds2, entropies2, label='all threshold entropies')
ax[2].plot(iter_thresholds3, iter_entropies3, label='optimization path')
ax[2].scatter(iter_thresholds3, iter_entropies3, c='C1')
ax[2].legend(loc='upper right')
plt.show()
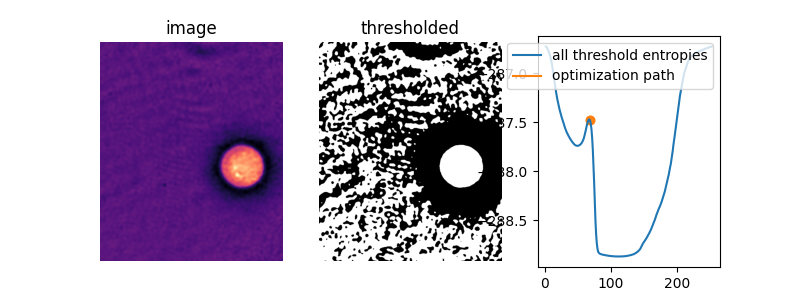
为了了解发生了什么,让我们定义一个函数 li_gradient,它复制了 Li 方法的内部循环并返回从当前阈值到下一个阈值的 变化。当这个梯度为 0 时,我们处于所谓的 稳定点,Li 返回这个值。当它为负时,下一个阈值猜测将更低,当它为正时,下一个猜测将更高。
在下图中,我们展示了当初始猜测在熵峰值的*右侧*时,交叉熵和Li更新路径。我们叠加了阈值更新梯度,标记了0梯度线和默认初始猜测 threshold_li。
def li_gradient(image, t):
"""Find the threshold update at a given threshold."""
foreground = image > t
mean_fore = np.mean(image[foreground])
mean_back = np.mean(image[~foreground])
t_next = (mean_back - mean_fore) / (np.log(mean_back) - np.log(mean_fore))
dt = t_next - t
return dt
iter_thresholds4 = []
opt_threshold4 = filters.threshold_li(
cell, initial_guess=68, iter_callback=iter_thresholds4.append
)
iter_entropies4 = [_cross_entropy(cell, t) for t in iter_thresholds4]
print(len(iter_thresholds4), 'examined, optimum:', opt_threshold4)
gradients = [li_gradient(cell, t) for t in thresholds2]
fig, ax1 = plt.subplots()
ax1.plot(thresholds2, entropies2)
ax1.plot(iter_thresholds4, iter_entropies4)
ax1.scatter(iter_thresholds4, iter_entropies4, c='C1')
ax1.set_xlabel('threshold')
ax1.set_ylabel('cross entropy', color='C0')
ax1.tick_params(axis='y', labelcolor='C0')
ax2 = ax1.twinx()
ax2.plot(thresholds2, gradients, c='C3')
ax2.hlines(
[0], xmin=thresholds2[0], xmax=thresholds2[-1], colors='gray', linestyles='dashed'
)
ax2.vlines(
np.mean(cell),
ymin=np.min(gradients),
ymax=np.max(gradients),
colors='gray',
linestyles='dashed',
)
ax2.set_ylabel(r'$\Delta$(threshold)', color='C3')
ax2.tick_params(axis='y', labelcolor='C3')
fig.tight_layout()
plt.show()
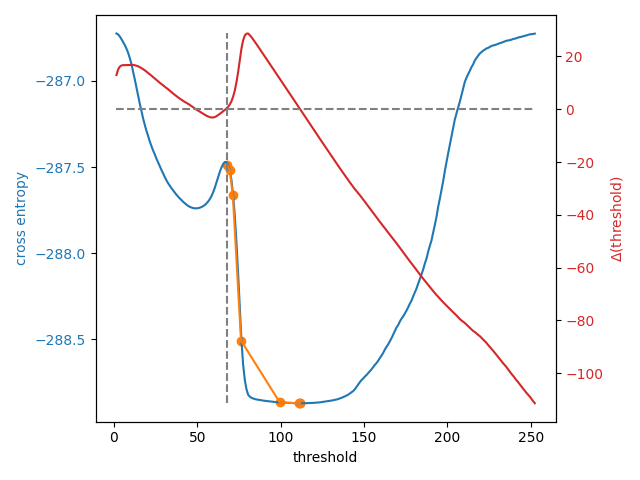
8 examined, optimum: 111.68876119648344
除了允许用户提供一个数字作为初始猜测外,skimage.filters.threshold_li() 还可以接收一个从图像强度中进行猜测的函数,就像 numpy.mean() 默认所做的那样。当需要处理许多范围不同的图像时,这可能是一个不错的选择。
def quantile_95(image):
# you can use np.quantile(image, 0.95) if you have NumPy>=1.15
return np.percentile(image, 95)
iter_thresholds5 = []
opt_threshold5 = filters.threshold_li(
cell, initial_guess=quantile_95, iter_callback=iter_thresholds5.append
)
iter_entropies5 = [_cross_entropy(cell, t) for t in iter_thresholds5]
print(len(iter_thresholds5), 'examined, optimum:', opt_threshold5)
fig, ax1 = plt.subplots()
ax1.plot(thresholds2, entropies2)
ax1.plot(iter_thresholds5, iter_entropies5)
ax1.scatter(iter_thresholds5, iter_entropies5, c='C1')
ax1.set_xlabel('threshold')
ax1.set_ylabel('cross entropy', color='C0')
ax1.tick_params(axis='y', labelcolor='C0')
plt.show()
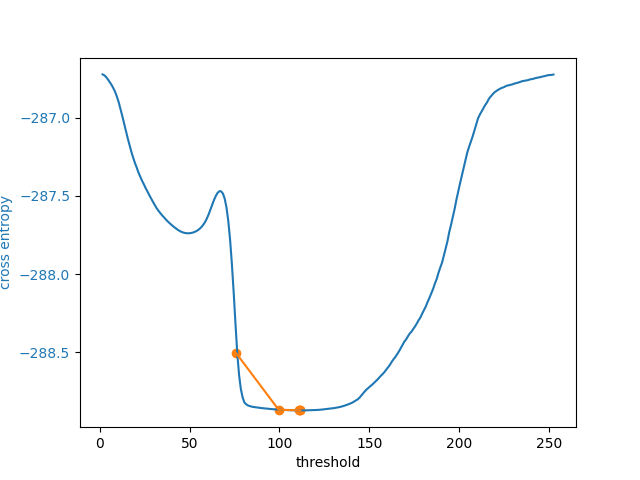
5 examined, optimum: 111.68876119648344
脚本总运行时间: (0 分钟 3.545 秒)
