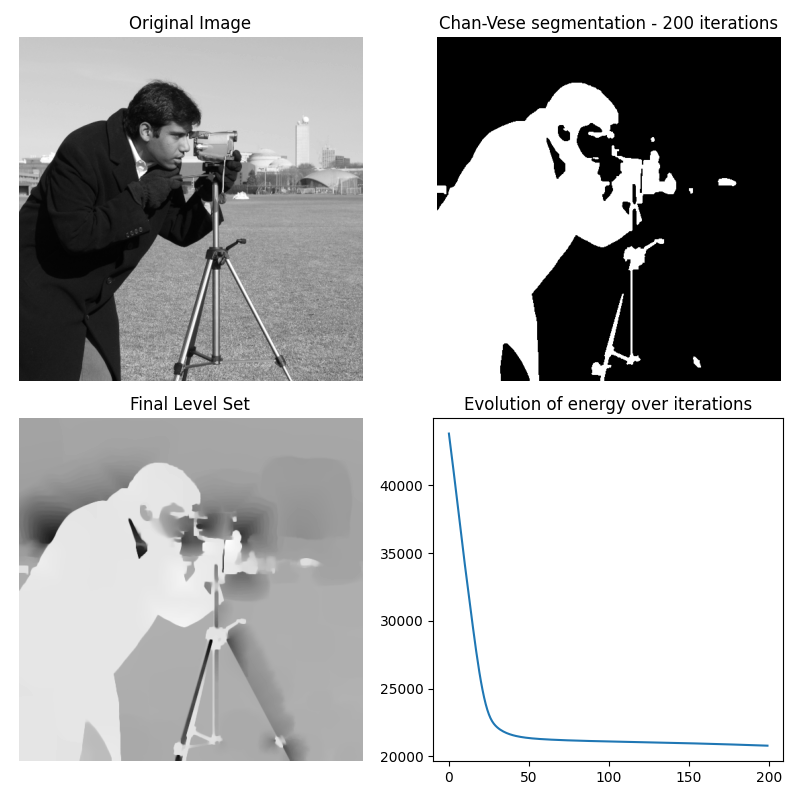
Chan-Vese 分割

Chan-Vese分割算法旨在分割没有清晰定义边界的物体。该算法基于水平集，这些水平集通过迭代演化以最小化一个能量，该能量由加权值定义，对应于分割区域外平均值的强度差之和、分割区域内平均值的强度差之和，以及依赖于分割区域边界长度的项。

该算法由Tony Chan和Luminita Vese首次提出，发表在《一个没有边缘的活动轮廓模型》[1]_中。另见[2]_，[3]。

该算法的实现略有简化，因为在原始论文中描述的面积因子 ‘nu’ 未被实现，并且仅适用于灰度图像。

lambda1 和 lambda2 的典型值为 1。如果 ‘背景’ 在分布上与分割对象非常不同（例如，一张均匀的黑色图像，其中有强度各异的图形），那么这些值应该彼此不同。

mu 的典型值介于 0 和 1 之间，尽管在处理轮廓非常不明确的形状时可以使用更高的值。

该算法还返回一个值列表，对应于每次迭代的能量。这可以用来调整上述各种参数。

参考文献

[1]

一个没有边缘的活动轮廓模型，Tony Chan 和 Luminita Vese，计算机视觉中的尺度空间理论，1999年，DOI:10.1007/3-540-48236-9_13

[2]

Chan-Vese 分割, Pascal Getreuer, 在线图像处理, 2 (2012), 页码. 214-224, DOI:10.5201/ipol.2012.g-cv

[3]

Chan-Vese算法 - 项目报告, Rami Cohen, 2011 arXiv:1107.2782

import matplotlib.pyplot as plt
from skimage import data, img_as_float
from skimage.segmentation import chan_vese

image = img_as_float(data.camera())
# Feel free to play around with the parameters to see how they impact the result
cv = chan_vese(
    image,
    mu=0.25,
    lambda1=1,
    lambda2=1,
    tol=1e-3,
    max_num_iter=200,
    dt=0.5,
    init_level_set="checkerboard",
    extended_output=True,
)

fig, axes = plt.subplots(2, 2, figsize=(8, 8))
ax = axes.flatten()

ax[0].imshow(image, cmap="gray")
ax[0].set_axis_off()
ax[0].set_title("Original Image", fontsize=12)

ax[1].imshow(cv[0], cmap="gray")
ax[1].set_axis_off()
title = f'Chan-Vese segmentation - {len(cv[2])} iterations'
ax[1].set_title(title, fontsize=12)

ax[2].imshow(cv[1], cmap="gray")
ax[2].set_axis_off()
ax[2].set_title("Final Level Set", fontsize=12)

ax[3].plot(cv[2])
ax[3].set_title("Evolution of energy over iterations", fontsize=12)

fig.tight_layout()
plt.show()