splprep#
- scipy.interpolate.splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None, full_output=0, nest=None, per=0, quiet=1)[源代码][源代码]#
找到 N 维曲线的 B 样条表示。
给定一个包含 N 个一维数组的列表 x,它们表示在 N 维空间中由 u 参数化的曲线,找到一个平滑的近似样条曲线 g(u)。使用 FITPACK 中的 FORTRAN 例程 parcur。
- 参数:
- xarray_like
表示曲线的样本向量数组列表。
- w类似数组, 可选
严格正的秩-1权重数组,长度与 x[0] 相同。这些权重用于计算加权最小二乘样条拟合。如果 x 值的误差的标准差由向量 d 给出,那么 w 应该是 1/d。默认是
ones(len(x[0]))。- u类似数组, 可选
参数值的数组。如果没有给出,这些值会自动计算为
M = len(x[0]),其中v[0] = 0
v[i] = v[i-1] + distance(x[i], x[i-1])
u[i] = v[i] / v[M-1]
- ub, ueint, 可选
参数区间端点。默认值为 u[0] 和 u[-1]。
- kint, 可选
样条的度数。推荐使用三次样条。应避免使用偶数值的 k,特别是在 s 值较小的情况下。
1 <= k <= 5,默认值为 3。- 任务int, 可选
如果 task==0(默认),找到给定平滑因子 s 的 t 和 c。如果 task==1,找到平滑因子 s 的另一个值的 t 和 c。必须先前对同一组数据调用过 task=0 或 task=1。如果 task=-1,找到给定节点 t 的加权最小二乘样条。
- sfloat, 可选
一个平滑条件。平滑的程度由满足以下条件决定:
sum((w * (y - g))**2,axis=0) <= s,其中 g(x) 是 (x,y) 的平滑插值。用户可以使用 s 来控制拟合的接近度和平滑度之间的权衡。较大的 s 意味着更多的平滑,而较小的 s 值表示较少的平滑。推荐的 s 值取决于权重 w。如果权重代表 y 的标准差的倒数,那么一个好的 s 值应在范围(m-sqrt(2*m),m+sqrt(2*m))内找到,其中 m 是 x、y 和 w 中的数据点数。- t数组,可选
task=-1所需的节点。必须至少有2*k+2个节点。- 完整输出int, 可选
如果非零,则返回可选输出。
- 嵌套int, 可选
用于帮助确定存储空间的样条曲线结点总数的高估。默认情况下,nest=m/2。总是足够大的是nest=m+k+1。
- 每int, 可选
如果非零,数据点被认为是周期性的,周期为
x[m-1] - x[0],并返回一个平滑的周期性样条近似。y[m-1]和w[m-1]的值不被使用。- 安静int, 可选
非零值以抑制消息。
- 返回:
- tck元组
一个元组
(t,c,k),包含节点向量、B样条系数和样条的阶数。- u数组
参数值的数组。
- fp浮动
样条逼近的残差平方的加权和。
- ier整数
关于 splrep 成功的整数标志。如果 ier <= 0,则表示成功。如果 ier 在 [1,2,3] 中,则发生了错误但未引发。否则会引发错误。
- 消息str
与整数标志 ier 对应的错误信息。
参见
注释
参见
splev以评估样条及其导数。维度数 N 必须小于 11。c 数组中的系数数量比节点数量
len(t)少k+1。这与splrep不同,后者将系数数组零填充以使其长度与节点数组相同。这些额外的系数被评估例程splev和BSpline忽略。参考文献
[1]P. Dierckx, “Algorithms for smoothing data with periodic and parametric splines, Computer Graphics and Image Processing”, 20 (1982) 171-184.
[2]P. Dierckx, “Algorithms for smoothing data with periodic and parametric splines”, report tw55, Dept. Computer Science, K.U.Leuven, 1981.
[3]P. Dierckx, “Curve and surface fitting with splines”, Monographs on Numerical Analysis, Oxford University Press, 1993.
示例
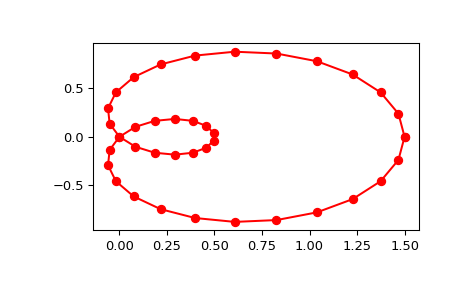
在极坐标中生成一个蜗线曲线的离散化:
>>> import numpy as np >>> phi = np.linspace(0, 2.*np.pi, 40) >>> r = 0.5 + np.cos(phi) # polar coords >>> x, y = r * np.cos(phi), r * np.sin(phi) # convert to cartesian
并插入:
>>> from scipy.interpolate import splprep, splev >>> tck, u = splprep([x, y], s=0) >>> new_points = splev(u, tck)
注意,(i) 我们通过使用 s=0 强制插值,(ii) 参数化,
u,是自动生成的。现在绘制结果:>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.plot(x, y, 'ro') >>> ax.plot(new_points[0], new_points[1], 'r-') >>> plt.show()