scipy.signal.

双线性_zpk

scipy.signal.bilinear_zpk(z, p, k, fs)

使用双线性变换从模拟滤波器返回数字IIR滤波器。

使用Tustin方法将一组极点和零点从模拟s平面转换到数字z平面，该方法用 2*fs*(z-1) / (z+1) 替换 s，保持频率响应的形状。

参数:

zarray_like

模拟滤波器传递函数的零点。

parray_like

模拟滤波器传递函数的极点。

k浮动

模拟滤波器传递函数的系统增益。

fs浮动

采样率，作为普通频率（例如，赫兹）。此函数中没有进行预扭曲。

返回:

zndarray

变换后的数字滤波器传递函数的零点。

pndarray

变换后的数字滤波器传递函数的极点。

k浮动

变换后的数字滤波器的系统增益。

参见

lp2lp_zpk, lp2hp_zpk, lp2bp_zpk, lp2bs_zpk

bilinear

注释

Added in version 1.1.0.

示例

Try it in your browser!

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

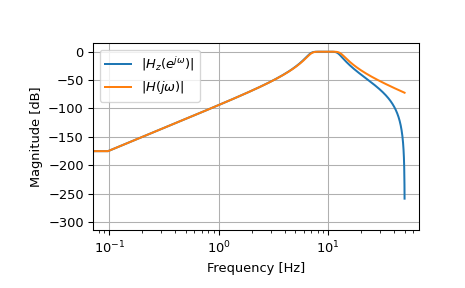
>>> fs = 100
>>> bf = 2 * np.pi * np.array([7, 13])
>>> filts = signal.lti(*signal.butter(4, bf, btype='bandpass', analog=True,
...                                   output='zpk'))
>>> filtz = signal.lti(*signal.bilinear_zpk(filts.zeros, filts.poles,
...                                         filts.gain, fs))
>>> wz, hz = signal.freqz_zpk(filtz.zeros, filtz.poles, filtz.gain)
>>> ws, hs = signal.freqs_zpk(filts.zeros, filts.poles, filts.gain,
...                           worN=fs*wz)
>>> plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hz).clip(1e-15)),
...              label=r'$|H_z(e^{j \omega})|$')
>>> plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hs).clip(1e-15)),
...              label=r'$|H(j \omega)|$')
>>> plt.legend()
>>> plt.xlabel('Frequency [Hz]')
>>> plt.ylabel('Magnitude [dB]')
>>> plt.grid(True)

Go BackOpen In Tab