kaiserord#
- scipy.signal.kaiserord(ripple, width)[源代码][源代码]#
确定Kaiser窗方法的滤波器窗口参数。
此函数返回的参数通常用于使用窗口法创建有限脉冲响应滤波器,使用
firwin或firwin2。- 参数:
- ripple浮动
滤波器频率响应幅值与期望滤波器频率响应幅值之间偏差的上限(以dB为单位,不包括任何过渡区间的频率)。也就是说,如果w是以奈奎斯特频率为单位的频率分数,A(w)是滤波器的实际频率响应,D(w)是期望的频率响应,设计要求是:
abs(A(w) - D(w))) < 10**(-ripple/20)
对于 0 <= w <= 1 且 w 不在过渡区间内。
- 宽度浮动
过渡区域的宽度,标准化后1对应于π弧度/样本。也就是说,频率表示为奈奎斯特频率的分数。
- 返回:
- numtaps整数
Kaiser窗口的长度。
- beta浮动
Kaiser 窗口的 beta 参数。
注释
有几种方法可以获得Kaiser窗口:
signal.windows.kaiser(numtaps, beta, sym=True)signal.get_window(beta, numtaps)signal.get_window(('kaiser', beta), numtaps)
使用Kaiser发现的实验方程。
参考文献
Oppenheim, Schafer, “离散时间信号处理”, 第475-476页。
示例
我们将使用Kaiser窗方法来设计一个低通FIR滤波器,用于以1000 Hz采样的信号。
我们希望在阻带中至少有65 dB的衰减,并且在通带中增益的变化不应超过0.5%。
我们希望截止频率为175 Hz,通带和阻带之间的过渡带宽为24 Hz。也就是说,在频带[0, 163]内,增益变化不超过0.5%,而在频带[187, 500]内,信号至少衰减65 dB。
>>> import numpy as np >>> from scipy.signal import kaiserord, firwin, freqz >>> import matplotlib.pyplot as plt >>> fs = 1000.0 >>> cutoff = 175 >>> width = 24
Kaiser方法仅接受一个参数来控制通带波纹和阻带衰减,因此我们使用两者中更严格的一个。在这种情况下,通带波纹为0.005,即46.02 dB,因此我们将使用65 dB作为设计参数。
使用
kaiserord来确定滤波器的长度和Kaiser窗口的参数。>>> numtaps, beta = kaiserord(65, width/(0.5*fs)) >>> numtaps 167 >>> beta 6.20426
使用
firwin来创建 FIR 滤波器。>>> taps = firwin(numtaps, cutoff, window=('kaiser', beta), ... scale=False, fs=fs)
计算滤波器的频率响应。
w是频率数组,h是对应的频率响应复数数组。>>> w, h = freqz(taps, worN=8000) >>> w *= 0.5*fs/np.pi # Convert w to Hz.
计算滤波器响应的幅度与理想低通滤波器的偏差。过渡区域中的值设置为
nan,因此它们不会出现在图中。>>> ideal = w < cutoff # The "ideal" frequency response. >>> deviation = np.abs(np.abs(h) - ideal) >>> deviation[(w > cutoff - 0.5*width) & (w < cutoff + 0.5*width)] = np.nan
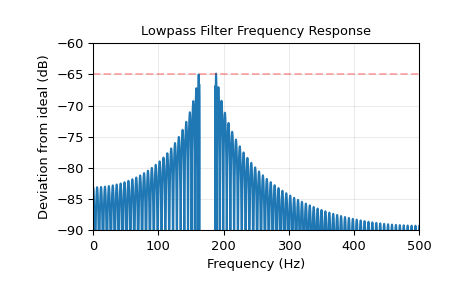
绘制偏差。仔细观察阻带左端,可以看到在第一个旁瓣中,65 dB衰减的要求被违反了约0.125 dB。这是Kaiser窗方法的常见现象。
>>> plt.plot(w, 20*np.log10(np.abs(deviation))) >>> plt.xlim(0, 0.5*fs) >>> plt.ylim(-90, -60) >>> plt.grid(alpha=0.25) >>> plt.axhline(-65, color='r', ls='--', alpha=0.3) >>> plt.xlabel('Frequency (Hz)') >>> plt.ylabel('Deviation from ideal (dB)') >>> plt.title('Lowpass Filter Frequency Response') >>> plt.show()