scipy.special.ive#

scipy.special.ive(v, z, out=None) = <ufunc 'ive'>#

第一类指数缩放修正贝塞尔函数。

定义为:

ive(v, z) = iv(v, z) * exp(-abs(z.real))

对于没有实部的虚数，返回未缩放的第一类贝塞尔函数 iv。

参数:

v类数组的浮点数: 订单。
z类似数组的浮点数或复数: 参数。
出ndarray，可选: 函数值的可选输出数组

返回:

标量或ndarray: 指数缩放修正贝塞尔函数的值。

参见

iv: 第一类修正贝塞尔函数
i0e: 此函数的更快实现，适用于阶数为0的情况
i1e: 此函数的更快速实现，适用于阶数1

注释

对于正数 v，会调用 AMOS [1] 的 zbesi 例程。它对小 z 使用幂级数，对大 abs(z) 使用渐近展开，对中间量级使用由 Wronskian 归一化的 Miller 算法和 Neumann 级数，以及对大阶数使用 \(I_v(z)\) 和 \(J_v(z)\) 的均匀渐近展开。必要时使用后向递归来生成序列或减少阶数。

上述计算在右半平面进行，并通过公式延续到左半平面，

\[ \begin{align}\begin{aligned}I_v(z \exp(\pm\imath\pi)) = \exp(\pm\pi v) I_v(z)\\I_v(z \exp(\pm\imath\pi)) = \exp(\pm\pi v) I_v(z)\end{aligned}\end{align} \]

(当 z 的实部为正时有效)。对于负的 v，公式

\[I_{-v}(z) = I_v(z) + \frac{2}{\pi} \sin(\pi v) K_v(z)\]

使用时，其中 \(K_v(z)\) 是第二类修正贝塞尔函数，使用 AMOS 例程 zbesk 进行评估。

ive 对于大参数 z 很有用：对于这些参数，iv 容易溢出，而 ive 不会，因为它采用了指数缩放。

参考文献

[1]

Donald E. Amos, “AMOS, 一个用于复数参数和非负阶贝塞尔函数的便携式软件包”, http://netlib.org/amos/

示例

在下面的例子中，iv 返回无穷大，而 ive 仍然返回一个有限数。

>>> from scipy.special import iv, ive
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> iv(3, 1000.), ive(3, 1000.)
(inf, 0.01256056218254712)

通过为 v 参数提供列表或 NumPy 数组作为参数，在不同阶数下评估函数在某一点的结果：

>>> ive([0, 1, 1.5], 1.)
array([0.46575961, 0.20791042, 0.10798193])

通过为 z 提供一个数组，在多个点上评估阶数为0的函数。

>>> points = np.array([-2., 0., 3.])
>>> ive(0, points)
array([0.30850832, 1.        , 0.24300035])

通过为 v 和 z 提供数组，在不同阶数下评估函数。两个数组都必须能够广播到正确的形状。要计算一维数组点在阶数 0、1 和 2 下的值：

>>> ive([[0], [1], [2]], points)
array([[ 0.30850832,  1.        ,  0.24300035],
       [-0.21526929,  0.        ,  0.19682671],
       [ 0.09323903,  0.        ,  0.11178255]])

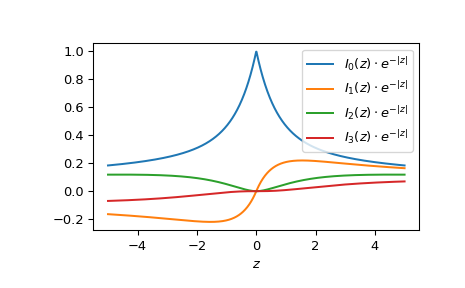
绘制从 -5 到 5 的 0 到 3 阶函数。

>>> fig, ax = plt.subplots()
>>> x = np.linspace(-5., 5., 1000)
>>> for i in range(4):
...     ax.plot(x, ive(i, x), label=fr'$I_{i!r}(z)\cdot e^{{-|z|}}$')
>>> ax.legend()
>>> ax.set_xlabel(r"$z$")
>>> plt.show()