scipy.special.ncfdtr#
- scipy.special.ncfdtr(dfn, dfd, nc, f, out=None) = <ufunc 'ncfdtr'>#
非中心F分布的累积分布函数。
非中心 F 描述了,
\[Z = \frac{X/d_n}{Y/d_d}\]其中 \(X\) 和 \(Y\) 是独立分布的,\(X\) 服从非中心 \(\chi^2\) 分布,非中心参数为 nc,自由度为 \(d_n\),而 \(Y\) 服从自由度为 \(d_d\) 的 \(\chi^2\) 分布。
- 参数:
- dfnarray_like
分子平方和的自由度。范围(0,无穷大)。
- dfdarray_like
分母平方和的自由度。范围 (0, ∞)。
- ncarray_like
非中心参数。应在范围 (0, 1e4) 内。
- farray_like
分位数,即积分的上限。
- 出ndarray,可选
函数结果的可选输出数组
- 返回:
- cdf标量或ndarray
计算的累积分布函数(CDF)。如果所有输入都是标量,返回值将为浮点数。否则,它将是一个数组。
参见
ncfdtri分位数函数;相对于 f 的
ncfdtr的逆函数。ncfdtridfd相对于 dfd 的
ncfdtr的逆函数。ncfdtridfn关于 dfn 的
ncfdtr的逆函数。ncfdtrinc关于 nc 的
ncfdtr的逆函数。
注释
CDFLIB [1] Fortran 例程 cdffnc 的包装器。
累积分布函数是使用 [2] 的公式 26.6.20 计算的。
\[ \begin{align}\begin{aligned}F(d_n, d_d, n_c, f) = \sum_{j=0}^\infty e^{-n_c/2} \frac{(n_c/2)^j}{j!} I_{x}(\frac{d_n}{2} + j, \frac{d_d}{2}),\\F(d_n, d_d, n_c, f) = \sum_{j=0}^\infty e^{-n_c/2} \frac{(n_c/2)^j}{j!} I_{x}(\frac{d_n}{2} + j, \frac{d_d}{2}),\end{aligned}\end{align} \]其中 \(I\) 是正则化不完全贝塔函数,且 \(x = f d_n/(f d_n + d_d)\)。
此例程所需的计算时间与非中心性参数 nc 成正比。此参数的极大值会消耗大量计算机资源。这就是搜索范围被限制在10,000的原因。
参考文献
[1]Barry Brown, James Lovato, 和 Kathy Russell, CDFLIB: 累积分布函数、逆函数及其他参数的Fortran例程库。
[2]Milton Abramowitz 和 Irene A. Stegun 编。《带有公式、图表和数学表格的数学函数手册》。纽约:Dover,1972年。
示例
>>> import numpy as np >>> from scipy import special >>> from scipy import stats >>> import matplotlib.pyplot as plt
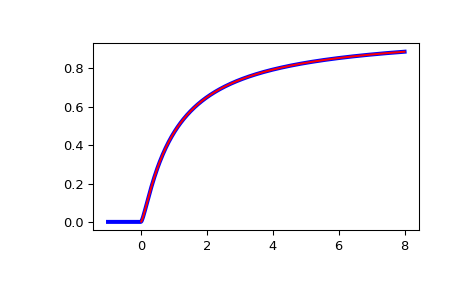
绘制非中心 F 分布的 CDF,其中 nc=0。与 scipy.stats 中的 F 分布进行比较:
>>> x = np.linspace(-1, 8, num=500) >>> dfn = 3 >>> dfd = 2 >>> ncf_stats = stats.f.cdf(x, dfn, dfd) >>> ncf_special = special.ncfdtr(dfn, dfd, 0, x)
>>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> ax.plot(x, ncf_stats, 'b-', lw=3) >>> ax.plot(x, ncf_special, 'r-') >>> plt.show()