多尺度图相关（MGC）

使用 scipy.stats.multiscale_graphcorr，我们可以对高维和非线性数据进行独立性检验。在开始之前，让我们导入一些有用的包：

>>> import numpy as np
>>> import matplotlib.pyplot as plt; plt.style.use('classic')
>>> from scipy.stats import multiscale_graphcorr

让我们使用一个自定义的绘图函数来绘制数据关系：

>>> def mgc_plot(x, y, sim_name, mgc_dict=None, only_viz=False,
...              only_mgc=False):
...     """绘制模拟和MGC图"""
...     if not only_mgc:
...         # 模拟
...         plt.figure(figsize=(8, 8))
...         ax = plt.gca()
...         ax.set_title(sim_name + " 模拟", fontsize=20)
...         ax.scatter(x, y)
...         ax.set_xlabel('X', fontsize=15)
...         ax.set_ylabel('Y', fontsize=15)
...         ax.axis('equal')
...         ax.tick_params(axis="x", labelsize=15)
...         ax.tick_params(axis="y", labelsize=15)
...         plt.show()
...     if not only_viz:
...         # 局部相关性图
...         plt.figure(figsize=(8,8))
...         ax = plt.gca()
...         mgc_map = mgc_dict["mgc_map"]
...         # 绘制热图
...         ax.set_title("局部相关性图", fontsize=20)
...         im = ax.imshow(mgc_map, cmap='YlGnBu')
...         # 颜色条
...         cbar = ax.figure.colorbar(im, ax=ax)
...         cbar.ax.set_ylabel("", rotation=-90, va="bottom")
...         ax.invert_yaxis()
...         # 关闭边框并创建白色网格。
...         for edge, spine in ax.spines.items():
...             spine.set_visible(False)
...         # 最优尺度
...         opt_scale = mgc_dict["opt_scale"]
...         ax.scatter(opt_scale[0], opt_scale[1],
...                    marker='X', s=200, color='red')
...         # 其他格式设置
...         ax.tick_params(bottom="off", left="off")
...         ax.set_xlabel('#X的邻居数', fontsize=15)
...         ax.set_ylabel('#Y的邻居数', fontsize=15)
...         ax.tick_params(axis="x", labelsize=15)
...         ax.tick_params(axis="y", labelsize=15)
...         ax.set_xlim(0, 100)
...         ax.set_ylim(0, 100)
...         plt.show()

让我们先来看一些线性数据：

>>> rng = np.random.default_rng()
>>> x = np.linspace(-1, 1, num=100)
>>> y = x + 0.3 * rng.random(x.size)

模拟关系可以绘制如下：

>>> mgc_plot(x, y, "线性", only_viz=True)

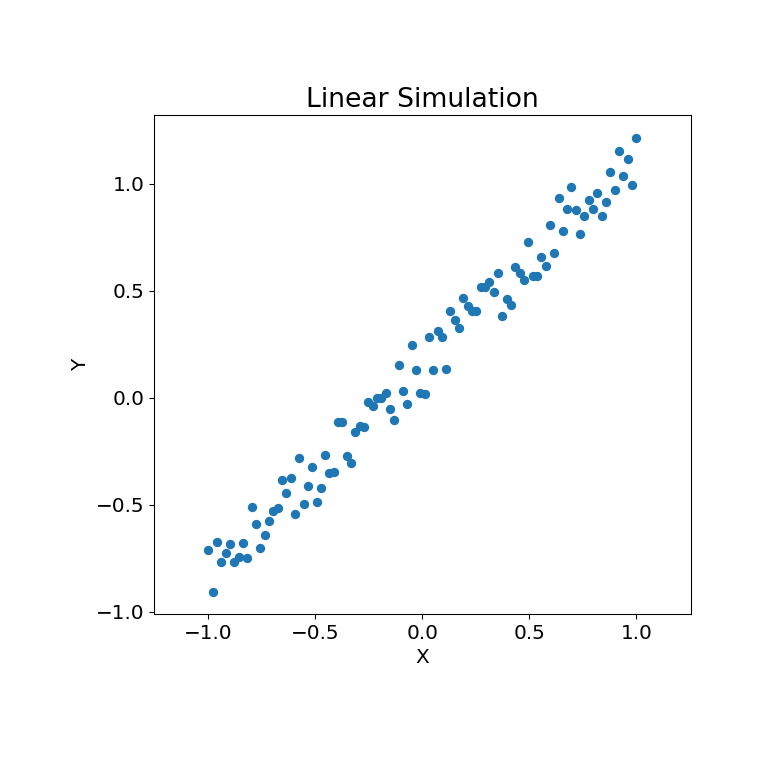
现在，我们可以看到测试统计量、p值和MGC图的可视化结果。最佳尺度在图中以红色“x”标记：

>>> stat, pvalue, mgc_dict = multiscale_graphcorr(x, y)
>>> print("MGC测试统计量: ", round(stat, 1))
MGC测试统计量:  1.0
>>> print("P值: ", round(pvalue, 1))
P值:  0.0
>>> mgc_plot(x, y, "线性", mgc_dict, only_mgc=True)

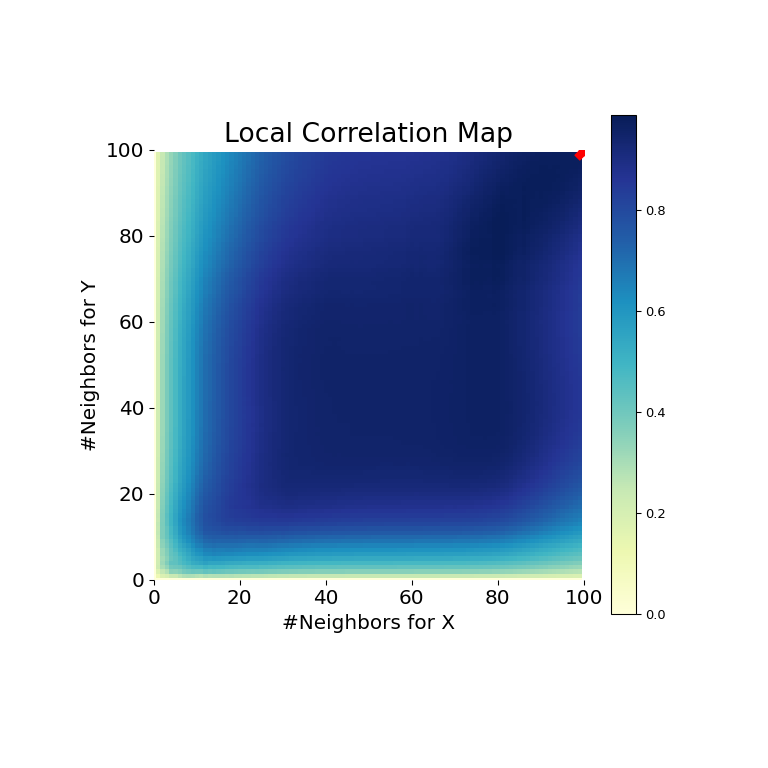
从这里可以清楚地看出，MGC能够确定输入数据矩阵之间的关系，因为p值非常低，而MGC测试统计量相对较高。MGC图表明存在**强线性关系**。直觉上，这是因为拥有更多的邻居将有助于识别 \(x\) 和 \(y\) 之间的线性关系。在这种情况下，最佳尺度**等同于全局尺度**，在图中以红色标记。

同样的方法可以用于非线性数据集。以下 \(x\) 和 \(y\) 数组来自一个非线性模拟：

>>> unif = np.array(rng.uniform(0, 5, size=100))
>>> x = unif * np.cos(np.pi * unif)
>>> y = unif * np.sin(np.pi * unif) + 0.4 * rng.random(x.size)

模拟关系可以绘制如下：

>>> mgc_plot(x, y, "Spiral", only_viz=True)

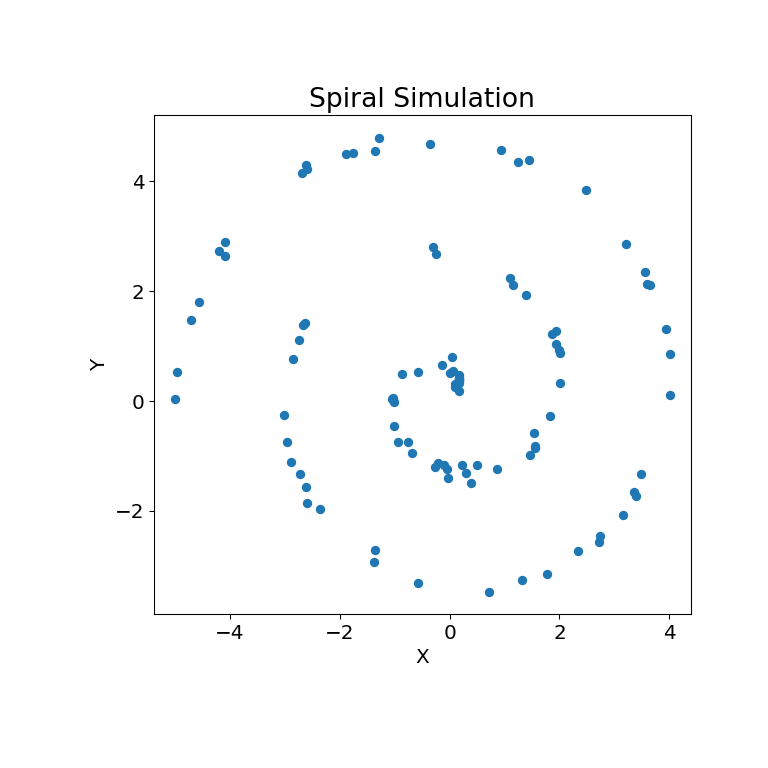
现在，我们可以看到测试统计量、p值和MGC图的可视化结果。最佳尺度在图中以红色“x”标记：

>>> stat, pvalue, mgc_dict = multiscale_graphcorr(x, y)
>>> print("MGC测试统计量: ", round(stat, 1))
MGC测试统计量:  0.2  # 随机
>>> print("P值: ", round(pvalue, 1))
P值:  0.0
>>> mgc_plot(x, y, "Spiral", mgc_dict, only_mgc=True)

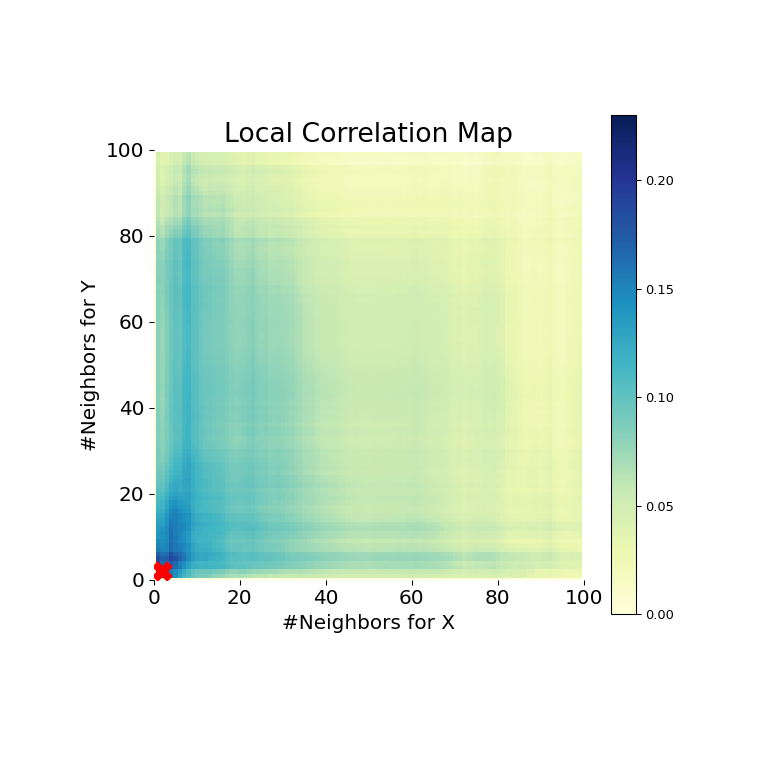
从这里可以清楚地看出，MGC再次能够确定关系，因为p值非常低，而MGC测试统计量相对较高。MGC图表明存在**强非线性关系**。在这种情况下，最佳尺度**等同于局部尺度**，在图中以红色标记。