核密度估计#
统计学中的一个常见任务是从一组数据样本中估计随机变量的概率密度函数(PDF)。这个任务被称为密度估计。最著名的工具是直方图。直方图是一个有用的可视化工具(主要是因为每个人都能理解它),但它并没有充分利用可用数据。核密度估计(KDE)是完成相同任务的更有效工具。scipy.stats.gaussian_kde 估计器可用于估计单变量和多变量数据的PDF。如果数据是单峰的,它的效果最好。
单变量估计#
我们从最少量的数据开始,以便了解 scipy.stats.gaussian_kde 的工作原理以及带宽选择的各个选项的作用。从PDF中采样的数据以蓝色短划线显示在图的底部(这称为地毯图):
>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> x1 = np.array([-7, -5, 1, 4, 5], dtype=np.float64)
>>> kde1 = stats.gaussian_kde(x1)
>>> kde2 = stats.gaussian_kde(x1, bw_method='silverman')
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x1, np.zeros(x1.shape), 'b+', ms=20) # 地毯图
>>> x_eval = np.linspace(-10, 10, num=200)
>>> ax.plot(x_eval, kde1(x_eval), 'k-', label="Scott's Rule")
>>> ax.plot(x_eval, kde2(x_eval), 'r-', label="Silverman's Rule")
>>> plt.show()
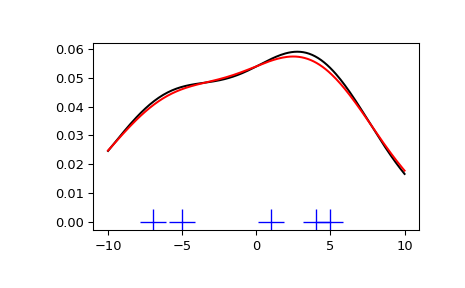
我们看到,Scott’s Rule 和 Silverman’s Rule 之间几乎没有区别,而且带宽选择在数据量有限的情况下可能有点太宽了。我们可以定义自己的带宽函数,以获得不太平滑的结果。
>>> def my_kde_bandwidth(obj, fac=1./5): ... """我们使用 Scott's Rule,乘以一个常数因子。"""… return np.power(obj.n, -1./(obj.d+4)) * fac
>>> fig = plt.figure() >>> ax = fig.add_subplot(111)>>> ax.plot(x1, np.zeros(x1.shape), 'b+', ms=20) # 地毯图 >>> kde3 = stats.gaussian_kde(x1, bw_method=my_kde_bandwidth) >>> ax.plot(x_eval, kde3(x_eval), 'g-', label="使用较小的带宽")>>> plt.show()
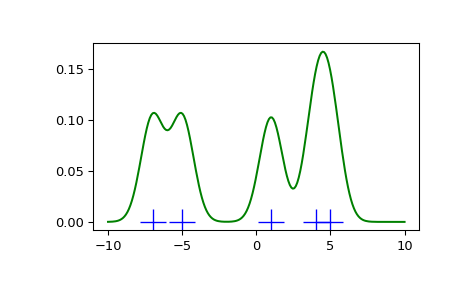
我们看到,如果将带宽设置得非常窄,得到的概率密度函数(PDF)估计仅仅是围绕每个数据点的多个高斯分布之和。
现在我们举一个更现实的例子,看看两种可用的带宽选择规则之间的差异。这些规则在(接近)正态分布的情况下表现良好,但对于相当非正态的单峰分布,它们也能合理地工作。作为一个非正态分布,我们采用自由度为5的学生T分布。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
rng = np.random.default_rng()
x1 = rng.normal(size=200) # random data, normal distribution
xs = np.linspace(x1.min()-1, x1.max()+1, 200)
kde1 = stats.gaussian_kde(x1)
kde2 = stats.gaussian_kde(x1, bw_method='silverman')
fig = plt.figure(figsize=(8, 6))
ax1 = fig.add_subplot(211)
ax1.plot(x1, np.zeros(x1.shape), 'b+', ms=12) # rug plot
ax1.plot(xs, kde1(xs), 'k-', label="Scott's Rule")
ax1.plot(xs, kde2(xs), 'b-', label="Silverman's Rule")
ax1.plot(xs, stats.norm.pdf(xs), 'r--', label="True PDF")
ax1.set_xlabel('x')
ax1.set_ylabel('Density')
ax1.set_title("Normal (top) and Student's T$_{df=5}$ (bottom) distributions")
ax1.legend(loc=1)
x2 = stats.t.rvs(5, size=200, random_state=rng) # random data, T distribution
xs = np.linspace(x2.min() - 1, x2.max() + 1, 200)
kde3 = stats.gaussian_kde(x2)
kde4 = stats.gaussian_kde(x2, bw_method='silverman')
ax2 = fig.add_subplot(212)
ax2.plot(x2, np.zeros(x2.shape), 'b+', ms=12) # rug plot
ax2.plot(xs, kde3(xs), 'k-', label="Scott's Rule")
ax2.plot(xs, kde4(xs), 'b-', label="Silverman's Rule")
ax2.plot(xs, stats.t.pdf(xs, 5), 'r--', label="True PDF")
ax2.set_xlabel('x')
ax2.set_ylabel('Density')
plt.show()
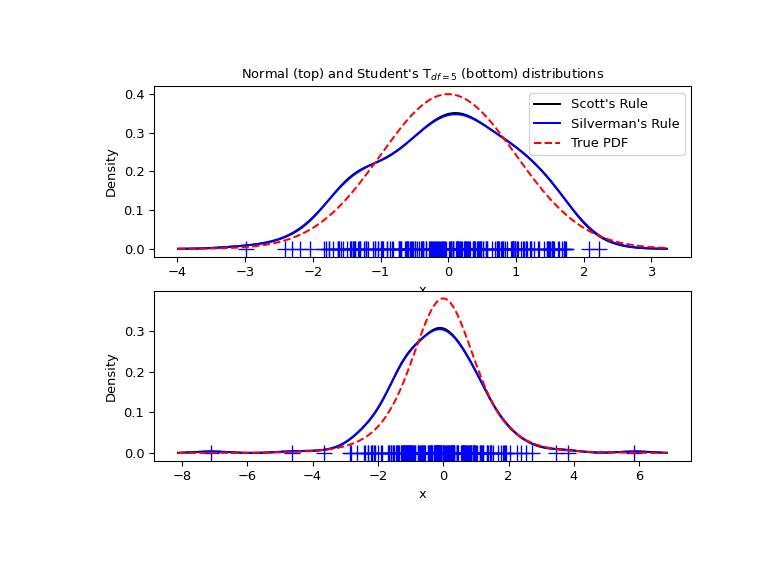
现在我们来看一个具有一个较宽和一个较窄高斯特征的双峰分布。我们预计这将是一个更难近似的密度,因为需要不同的带宽来准确解析每个特征。
>>> from functools import partial
>>> loc1, scale1, size1 = (-2, 1, 175)
>>> loc2, scale2, size2 = (2, 0.2, 50)
>>> x2 = np.concatenate([np.random.normal(loc=loc1, scale=scale1, size=size1),
... np.random.normal(loc=loc2, scale=scale2, size=size2)])
>>> x_eval = np.linspace(x2.min() - 1, x2.max() + 1, 500)
>>> kde = stats.gaussian_kde(x2)
>>> kde2 = stats.gaussian_kde(x2, bw_method='silverman')
>>> kde3 = stats.gaussian_kde(x2, bw_method=partial(my_kde_bandwidth, fac=0.2))
>>> kde4 = stats.gaussian_kde(x2, bw_method=partial(my_kde_bandwidth, fac=0.5))
>>> pdf = stats.norm.pdf
>>> bimodal_pdf = pdf(x_eval, loc=loc1, scale=scale1) * float(size1) / x2.size + \
... pdf(x_eval, loc=loc2, scale=scale2) * float(size2) / x2.size
>>> fig = plt.figure(figsize=(8, 6))
>>> ax = fig.add_subplot(111)
>>> ax.plot(x2, np.zeros(x2.shape), 'b+', ms=12)
>>> ax.plot(x_eval, kde(x_eval), 'k-', label="Scott's Rule")
>>> ax.plot(x_eval, kde2(x_eval), 'b-', label="Silverman's Rule")
>>> ax.plot(x_eval, kde3(x_eval), 'g-', label="Scott * 0.2")
>>> ax.plot(x_eval, kde4(x_eval), 'c-', label="Scott * 0.5")
>>> ax.plot(x_eval, bimodal_pdf, 'r--', label="Actual PDF")
>>> ax.set_xlim([x_eval.min(), x_eval.max()])
>>> ax.legend(loc=2)
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('Density')
>>> plt.show()
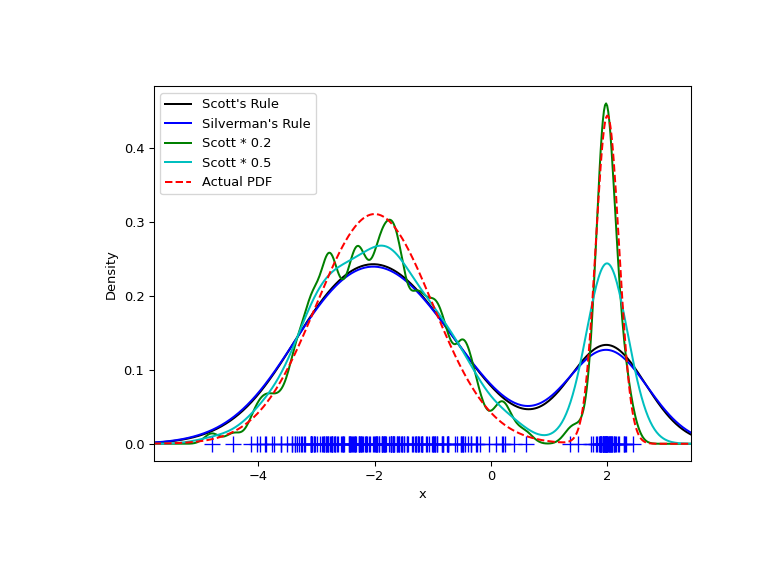
正如预期,由于双峰分布的两个特征具有不同的特征大小,KDE 并没有像我们希望的那样接近真实的 PDF。通过将默认带宽减半(Scott * 0.5),我们可以做得更好一些,而使用比默认值小 5 倍的带宽则不够平滑。然而,在这种情况下,我们真正需要的是非均匀(自适应)带宽。
多元估计#
使用 scipy.stats.gaussian_kde,我们可以进行多元以及单变量估计。我们演示了双变量的情况。首先,我们生成一些随机数据,其中两个变量是相关的。
>>> def measure(n):
... """测量模型,返回两个耦合的测量值。"""
... m1 = np.random.normal(size=n)
... m2 = np.random.normal(scale=0.5, size=n)
... return m1+m2, m1-m2
>>> m1, m2 = measure(2000)
>>> xmin = m1.min()
>>> xmax = m1.max()
>>> ymin = m2.min()
>>> ymax = m2.max()
- 然后我们对数据应用 KDE:
>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j] >>> positions = np.vstack([X.ravel(), Y.ravel()]) >>> values = np.vstack([m1, m2]) >>> kernel = stats.gaussian_kde(values) >>> Z = np.reshape(kernel.evaluate(positions).T, X.shape)
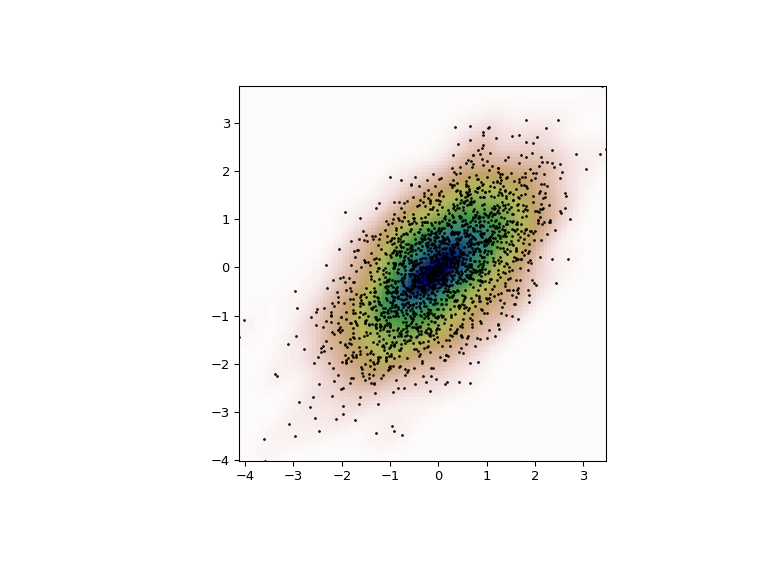
最后,我们将估计的二元分布绘制为颜色映射图,并在其上绘制单独的数据点。
>>> fig = plt.figure(figsize=(8, 6))
>>> ax = fig.add_subplot(111)
>>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r,
... extent=[xmin, xmax, ymin, ymax])
>>> ax.plot(m1, m2, 'k.', markersize=2)
>>> ax.set_xlim([xmin, xmax])
>>> ax.set_ylim([ymin, ymax])
>>> plt.show()