SciPy中的通用非均匀随机数采样#
SciPy提供了一个接口,用于许多通用非均匀随机数生成器,以从各种单变量连续和离散分布中采样随机变量。这些生成器使用了名为`UNU.RAN <http://statmath.wu.ac.at/software/unuran/>`__的快速C库的实现,以提高速度和性能。请参阅`UNU.RAN的文档 <http://statmath.wu.ac.at/software/unuran/doc/unuran.html>`__以深入了解这些方法。本教程和所有生成器的文档在很大程度上参考了该文档。
引言#
随机变量生成是研究如何从各种分布中生成随机变量的算法的小领域。通常假设存在一个均匀随机数生成器。这是一个程序,它生成一系列独立同分布的连续U(0,1)随机变量(即在区间(0,1)上的均匀随机变量)。当然,现实世界的计算机永远无法生成理想的随机数,也无法生成任意精度的数字,但最先进的均匀随机数生成器接近这一目标。因此,随机变量生成处理的问题是将这种U(0,1)随机数序列转换为非均匀随机变量。这些方法是通用的,并以黑箱方式工作。
一些实现这一目标的方法包括:
逆变换法:当累积分布函数的逆 \(F^{-1}\) 已知时,随机变量生成很容易。我们只需生成一个均匀U(0,1)分布的随机数U,并返回 \(X = F^{-1}(U)\)。由于逆变换的封闭形式解 很少有现成的逆函数可用,通常需要依赖于逆函数的近似(例如:
ndtri,stdtrit)。一般来说,特殊函数的实现相比UNU.RAN中的逆方法要慢得多。拒绝方法:拒绝方法,通常称为接受-拒绝方法,由John von Neumann在1951年提出 [1]。它涉及计算PDF的上限(也称为帽函数),并使用逆方法从这个上限生成一个随机变量,比如Y。然后可以在0到Y处的上限值之间抽取一个均匀随机数。如果这个数小于Y处的PDF值,则返回样本,否则拒绝它。参见
TransformedDensityRejection。均匀比方法:这是一种接受-拒绝方法,它使用最小边界矩形来构造帽函数。参见
scipy.stats.rvs_ratio_uniforms。离散分布的逆方法:与连续情况的不同之处在于,\(F\) 现在是一个阶梯函数。为了在计算机中实现这一点,使用了一种搜索算法,最简单的是*顺序搜索*。从U(0, 1)生成一个均匀随机数,并累加概率,直到累积概率超过均匀随机数。发生这种情况的索引即为所需的随机变量,并返回。
有关这些算法的更多详细信息可以在 UNU.RAN用户手册的附录 中找到。
在生成分布的随机变量时,两个因素对生成器的速度至关重要:设置步骤和实际采样。根据情况的不同,不同的生成器可能是最优的。例如,如果需要从给定分布中反复抽取大量样本, 固定形状参数的情况下,如果采样速度快,缓慢的设置是可以接受的。 这被称为固定参数情况。如果目标是生成不同形状参数(变化参数情况)的分布样本, 那么每次参数变化都需要重复的昂贵设置将导致性能非常低下。在这种情况下,快速的设置对于实现良好的性能至关重要。 下表概述了不同方法的设置和采样速度。
其中
pdf: 概率密度函数
dpdf: pdf的导数
cdf: 累积分布函数
要在SciPy中对大量连续分布应用数值反演方法NumericalInversePolynomial, 并尽量减少工作量,请查看`scipy.stats.sampling.FastGeneratorInversion`。
其中
pv: 概率向量
pmf: 概率质量函数
有关UNU.RAN中实现的生成器的更多详细信息,请参阅[2]_和[3]_。
接口的基本概念#
每个生成器在使用之前都需要进行设置。这可以通过实例化该类的对象来完成。大多数生成器需要一个分布对象作为输入,该对象包含PDF、CDF等所需方法的实现。除了分布对象外,还可以传递用于设置生成器的参数。还可以使用``domain``参数对分布进行截断。所有生成器都需要一个均匀随机数流,这些随机数被转换为给定分布的随机变量。这是通过传递一个包含NumPy BitGenerator的``random_state``参数来完成的,作为均匀随机数生成器。``random_state``可以是整数、numpy.random.Generator`或`numpy.random.RandomState。
警告
不建议使用NumPy < 1.19.0,因为它没有用于生成均匀随机数的快速Cython API,并且可能对于实际使用来说太慢。
所有生成器都有一个通用的``rvs``方法,可用于从给定分布中抽取样本。
以下是此接口的一个示例:
>>> from scipy.stats.sampling import TransformedDensityRejection
>>> from math import exp
>>>
>>> class StandardNormal:
... def pdf(self, x: float) -> float:
... # 注意不需要归一化常数
... return exp(-0.5 * x*x)
... def dpdf(self, x: float) -> float:
... return -x * exp(-0.5 * x*x)
...
>>> dist = StandardNormal()
>>>
>>> import numpy as np
>>> urng = np.random.default_rng()
>>> rng = TransformedDensityRejection(dist, random_state=urng)
如示例所示,我们首先初始化一个包含生成器所需方法实现的分布对象。在我们的例子中,我们使用了 TransformedDensityRejection (TDR) 方法,该方法需要 PDF 及其关于 ``x``(即变量)的导数。
注意
请注意,分布的方法(即 pdf、dpdf 等)不需要向量化。它们应接受并返回浮点数。
注意
也可以传递 SciPy 分布作为参数。然而,请注意,对象并不总是包含某些生成器(如 TDR 方法的 PDF 导数)所需的所有信息。依赖 SciPy 分布也可能由于方法(如 pdf 和 cdf)的向量化而降低性能。在这两种情况下,都可以实现一个包含所有必需方法且未向量化的自定义分布对象,如上例所示。如果希望对 SciPy 中定义的分布应用数值反演方法,请同时查看 scipy.stats.sampling.FastGeneratorInversion。
在上面的示例中,我们设置了一个 TransformedDensityRejection 方法的对象,用于从标准正态分布中采样。现在,我们可以通过调用 rvs 方法开始从我们的分布中采样:
>>> rng.rvs()
-1.526829048388144
>>> rng.rvs((5, 3))
array([[ 2.06206883, 0.15205036, 1.11587367],
[-0.30775562, 0.29879802, -0.61858268],
[-1.01049115, 0.78853694, -0.23060766],
[-0.60954752, 0.29071797, -0.57167182],
[ 0.9331694 , -0.95605208, 1.72195199]])
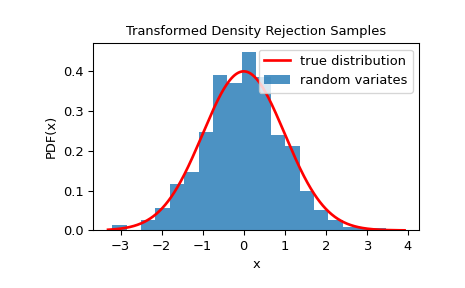
我们还可以通过可视化样本的直方图来检查样本是否从正确的分布中抽取:
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import norm
>>> from scipy.stats.sampling import TransformedDensityRejection
>>> from math import exp
>>>
>>> class StandardNormal:
... def pdf(self, x: float) -> float:
... # 注意不需要归一化常数
... return exp(-0.5 * x*x)
... def dpdf(self, x: float) -> float:
... return -x * exp(-0.5 * x*x)
...
>>>
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = TransformedDensityRejection(dist, random_state=urng)
>>> rvs = rng.rvs(size=1000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, num=1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Transformed Density Rejection Samples')
>>> plt.legend()
>>> plt.show()
备注
请注意 scipy.stats 中分布的 rvs 方法与这些生成器提供的 rvs 方法之间的区别。UNU.RAN 生成器必须被视为独立的,因为它们通常会产生与等效生成器不同的随机数流。
在 scipy.stats 中,对于任何种子,分布的实现方式可能会有所不同。scipy.stats.rv_continuous 中 rvs 的实现通常依赖于 NumPy 模块 numpy.random 来处理众所周知的分布(例如,正态分布、贝塔分布)以及其他分布的变换(例如,正态逆高斯分布 scipy.stats.norminvgauss 和 对数正态分布 scipy.stats.lognorm)。如果没有实现特定方法,scipy.stats.rv_continuous 默认使用 CDF 的数值反演方法,这种方法非常慢。由于 UNU.RAN 对均匀随机数的变换方式与 SciPy 或 NumPy 不同,即使对于相同的均匀随机数流,生成的随机变量流也会不同。例如,SciPy 的 scipy.stats.norm 和 UNU.RAN 的 TransformedDensityRejection 的随机数流即使使用相同的 random_state 也不会相同:
>>> from scipy.stats import norm
>>> from scipy.stats.sampling import TransformedDensityRejection
>>> from copy import copy
>>> dist = StandardNormal()
>>> urng1 = np.random.default_rng()
>>> urng1_copy = copy(urng1)
>>> rng = TransformedDensityRejection(dist, random_state=urng1)
>>> rng.rvs()
-1.526829048388144
>>> norm.rvs(random_state=urng1_copy)
1.3194816698862635 # 可能会有所不同
我们可以传递一个 domain 参数来截断分布:
>>> rng = TransformedDensityRejection(dist, domain=(-1, 1), random_state=urng)
>>> rng.rvs((5, 3))
array([[-0.99865691, 0.38104014, 0.31633526], # 可能会有所不同
[ 0.88433909, -0.45181849, 0.78574461],
[ 0.3337244 , 0.12924307, 0.40499404],
[-0.51865761, 0.43252222, -0.6514866 ],
[-0.82666174, 0.71525582, 0.49006743]])
无效和错误的参数由SciPy或UNU.RAN处理。后者抛出一个遵循通用格式的:class:UNURANError:
UNURANError: [objid: <对象ID>] <错误代码>: <原因> => <错误类型>
其中:
<对象ID>是UNU.RAN给出的对象ID<错误代码>是表示错误类型的错误代码。<原因>是错误发生的原因。<错误类型>是错误类型的简短描述。
<原因> 显示了导致错误的原因。这本身应该包含足够的信息来帮助调试错误。此外,<错误ID> 和 <错误类型> 可以用于调查UNU.RAN中不同类别的错误。所有错误代码及其描述的完整列表可以在 UNU.RAN用户手册的第8.4节 中找到。
下面显示了一个由UNU.RAN生成的错误的示例:
UNURANError: [objid: TDR.003] 50 : PDF(x) < 0.! => (生成器) (可能) 无效数据
这表明UNU.RAN未能初始化ID为``TDR.003``的对象,因为PDF < 0,即负值。这属于“生成器可能的无效数据”类型,错误代码为50。
UNU.RAN抛出的警告也遵循相同的格式。