离散别名瓮(DAU)#
必需:概率向量(PV)或概率质量函数(PMF)以及有限域
速度:
设置:慢(与向量长度成线性关系)
采样:非常快
DAU 从具有任意但有限长度 N 的概率向量(PV)的分布中进行采样。该算法基于 A.J. Walker 的巧妙方法,并需要一个大小至少为 N 的表格。它每次生成随机变量只需要一个随机数和一次比较。构建表格的设置时间为 O(N)。
>>> import numpy as np
>>> from scipy.stats.sampling import DiscreteAliasUrn
>>>
>>> pv = [0.18, 0.02, 0.8]
>>> urng = np.random.default_rng()
>>> rng = DiscreteAliasUrn(pv, random_state=urng)
>>> rng.rvs()
0 # 可能会有所不同
默认情况下,概率向量的索引从 0 开始。然而,这可以通过传递一个 domain 参数来改变。当 domain 与 PV 一起给出时,它会将分布从 (0, len(pv)) 重新定位到 (domain[0], domain[0] + len(pv))。在这种情况下,domain[1] 被忽略。
>>> rng = DiscreteAliasUrn(pv, domain=(10, 13), random_state=urng)
>>> rng.rvs()
12 # 可能会有所不同
当没有给出概率向量而是给出了 PMF 时,该方法也适用。在这种情况下,还必须通过显式传递 domain 参数或通过在分布对象中提供 support 方法来给出有界(有限)域:
>>> class Distribution:
... def __init__(self, c):
... self.c = c
... def pmf(self, x):
... return x**self.c
... def support(self):
... return (0, 10)
...
>>> dist = Distribution(2)
>>> rng = DiscreteAliasUrn(dist, random_state=urng)
>>> rng.rvs()
10 # 可能会有所不同
>>> import matplotlib.pyplot as plt
>>> from scipy.stats.sampling import DiscreteAliasUrn
>>> class Distribution:
... def __init__(self, c):
... self.c = c
... def pmf(self, x):
... return x**self.c
... def support(self):
... return (0, 10)
...
>>> dist = Distribution(2)
>>> urng = np.random.default_rng()
>>> rng = DiscreteAliasUrn(dist, random_state=urng)
>>> rvs = rng.rvs(1000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> x = np.arange(1, 11)
>>> fx = dist.pmf(x)
>>> fx = fx / fx.sum()
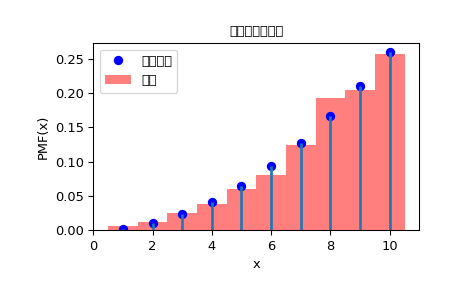
>>> ax.plot(x, fx, 'bo', label='真实分布')
>>> ax.vlines(x, 0, fx, lw=2)
>>> ax.hist(rvs, bins=np.r_[x, 11]-0.5, density=True, alpha=0.5, color='r',
... label='样本')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PMF(x)')
>>> ax.set_title('离散别名瓮样本')
>>> plt.legend()
>>> plt.show()
注意
由于 DiscreteAliasUrn 期望 PMF 具有签名
def pmf(self, x: float) -> float,它首先使用 np.vectorize 对
PMF 进行向量化,然后在域中的所有点上进行评估。但如果 PMF 已经向量化,
直接在域中的每个点上进行评估并传递获得的 PV 以及域会快得多。
例如,SciPy 的离散分布的 pmf 方法是向量化的,可以通过以下方式获得 PV:
>>> from scipy.stats import binom
>>> from scipy.stats.sampling import DiscreteAliasUrn
>>> dist = binom(10, 0.2) # 分布对象
>>> domain = dist.support() # 你的分布的域
>>> x = np.arange(domain[0], domain[1] + 1)
>>> pv = dist.pmf(x)
>>> rng = DiscreteAliasUrn(pv, domain=domain)
这里需要域来重新定位分布。
性能可以通过设置使用的表的大小来略微影响,该大小可以通过传递 urn_factor 参数来更改。
>>> # 使用长度为 PV 两倍的表。
>>> urn_factor = 2
>>> rng = DiscreteAliasUrn(pv, urn_factor=urn_factor, random_state=urng)
>>> rng.rvs()
2 # 可能会有所不同
备注
建议将此参数保持在 2 以下。