概率分布#

已经实现了两个通用的分布类，用于封装连续随机变量和离散随机变量。使用这些类已经实现了超过 80 个连续随机变量 (RVs) 和 10 个离散随机变量。关于各个分布的数学参考信息，请参阅连续统计分布和离散统计分布。

所有的统计函数都位于子包 scipy.stats 中，并且可以通过 stats 子包的 docstring 获得这些函数和随机变量的相当完整的列表。

在下面的讨论中，我们主要关注连续 RVs。几乎所有内容也适用于离散变量，但我们在这里指出一些差异：离散分布的特定点。

在下面的代码示例中，我们假设 scipy.stats 包被导入为

>>> from scipy import stats

在某些情况下，我们还假设个别对象被导入为

>>> from scipy.stats import norm

所有分布

获取帮助#

首先，所有分布都附带有帮助函数。要获取一些基本信息，我们打印相关的 docstring：print(stats.norm.__doc__)。

要查找分布的支持，即分布的上限和下限，请调用：

>>> print('分布的下限: %s, 上限: %s' % norm.support())
分布的下限: -inf, 上限: inf

我们可以使用 dir(norm) 列出分布的所有方法和属性。事实证明，一些方法是私有的，尽管它们没有这样命名（它们的名称不以开头下划线开头），例如 veccdf，仅用于内部计算（这些方法在尝试使用时会给出警告）。使用它们（并且将在某个时候被移除）。

要获取*真正的*主方法，我们列出冻结分布的方法。（我们将在下面解释`frozen`分布的含义）。

>>> rv = norm()
>>> dir(rv)  # 重新格式化
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__',
 '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__',
 '__init__', '__le__', '__lt__', '__module__', '__ne__', '__new__',
 '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__',
 '__str__', '__subclasshook__', '__weakref__', 'a', 'args', 'b', 'cdf',
 'dist', 'entropy', 'expect', 'interval', 'isf', 'kwds', 'logcdf',
 'logpdf', 'logpmf', 'logsf', 'mean', 'median', 'moment', 'pdf', 'pmf',
 'ppf', 'random_state', 'rvs', 'sf', 'stats', 'std', 'var']

最后，我们可以通过内省获取可用分布的列表：

>>> dist_continu = [d for d in dir(stats) if
...                 isinstance(getattr(stats, d), stats.rv_continuous)]
>>> dist_discrete = [d for d in dir(stats) if
...                  isinstance(getattr(stats, d), stats.rv_discrete)]
>>> print('连续分布的数量: %d' % len(dist_continu))
连续分布的数量: 108
>>> print('离散分布的数量:   %d' % len(dist_discrete))
离散分布的数量:   20

常用方法#

连续随机变量的主要公共方法有：

rvs: 随机变量
pdf: 概率密度函数
cdf: 累积分布函数
sf: 生存函数（1-CDF）
ppf: 百分点函数（CDF的逆）
isf: 逆生存函数（SF的逆）
stats: 返回均值、方差、（Fisher的）偏度或（Fisher的）峰度
moment: 分布的非中心矩

让我们以正态随机变量为例。

>>> norm.cdf(0)
0.5

要计算在多个点的``cdf``，我们可以传递一个列表或一个numpy数组。

>>> norm.cdf([-1., 0, 1])
array([ 0.15865525,  0.5,  0.84134475])
>>> import numpy as np
>>> norm.cdf(np.array([-1., 0, 1]))
array([ 0.15865525,  0.5,  0.84134475])

因此，基本方法，如 pdf、cdf 等，都是向量化的。

其他常用方法也得到了支持：

>>> norm.mean(), norm.std(), norm.var()
(0.0, 1.0, 1.0)
>>> norm.stats(moments="mv")
(array(0.0), array(1.0))

要找到分布的中位数，我们可以使用百分位点函数 ppf，它是 cdf 的逆函数：

>>> norm.ppf(0.5)
0.0

要生成一系列随机变量，请使用 size 关键字参数：

>>> norm.rvs(size=3)
array([-0.35687759,  1.34347647, -0.11710531])   # 随机

不要认为 norm.rvs(5) 会生成 5 个变量：

>>> norm.rvs(5)
5.471435163732493  # 随机

在这里，没有关键字的 5 被解释为第一个可能的关键字参数 loc，它是所有连续分布所采用的一对关键字参数中的第一个。这使我们进入下一个小节的主题。

随机数生成#

绘制随机数依赖于 numpy.random 包中的生成器。在上面的示例中，特定的随机数流在运行之间是不可复现的。为了实现可复现性，您可以显式地种子一个随机数生成器。在 NumPy 中，生成器是 numpy.random.Generator 的一个实例。以下是创建生成器的规范方法：

>>> from numpy.random import default_rng
>>> rng = default_rng()

而固定种子可以这样做：

>>> # 不要复制这个值
>>> rng = default_rng(301439351238479871608357552876690613766)

警告

不要使用这个数字或常见的值，如 0。仅使用一小部分种子来实例化更大的状态空间意味着有一些初始状态是无法达到的。这

如果每个人都使用这些值，会产生一些偏差。获取种子的一种好方法是使用 numpy.random.SeedSequence：

>>> from numpy.random import SeedSequence
>>> print(SeedSequence().entropy)
301439351238479871608357552876690613766  # 随机

分布中的 random_state 参数接受 numpy.random.Generator 类的实例，或一个整数，该整数随后用于为内部 Generator 对象设定种子：

>>> norm.rvs(size=5, random_state=rng)
array([ 0.47143516, -1.19097569,  1.43270697, -0.3126519 , -0.72058873])  # 随机

更多信息，请参阅 NumPy 的文档。

要了解更多关于 SciPy 中实现的随机数采样器的信息，请参阅非均匀随机数采样教程和准蒙特卡罗教程

平移和缩放#

所有连续分布都接受 loc 和 scale 作为关键字参数，以调整分布的位置和尺度，例如，对于标准正态分布，位置是均值，尺度是标准差。

>>> norm.stats(loc=3, scale=4, moments="mv")
(array(3.0), array(16.0))

在许多情况下，随机变量 X 的标准化分布通过变换 (X - loc) / scale 获得。默认值为 loc = 0 和 scale = 1。

智能使用 loc 和 scale 可以帮助以多种方式修改标准分布。为了进一步说明缩放，均值为 \(1/\lambda\) 的指数分布随机变量的 cdf 由下式给出

\[F(x) = 1 - \exp(-\lambda x)\]

通过应用上述缩放规则，可以看出通过取 scale = 1./lambda 可以得到适当的尺度。

>>> from scipy.stats import expon
>>> expon.mean(scale=3.)
3.0

备注

需要形状参数的分布可能需要比简单应用 loc 和/或 scale 更复杂的操作才能达到所需的形式。例如，给定长度为 \(R\) 的常向量，其每个分量受到独立 N(0, \(\sigma^2\)) 扰动的情况下，2-D 向量长度的分布为 rice(\(R/\sigma\), scale= \(\sigma\))。第一个参数是一个需要与 \(x\) 一起缩放的形状参数。

均匀分布也很有趣：

>>> from scipy.stats import uniform
>>> uniform.cdf([0, 1, 2, 3, 4, 5], loc=1, scale=4)
array([ 0.  ,  0.  ,  0.25,  0.5 ,  0.75,  1.  ])

最后，回想一下前一段，我们留下了 norm.rvs(5) 的意义问题。事实证明，像这样调用一个分布时，第一个参数，即 5，会被传递来设置 loc 参数。让我们看看：

>>> np.mean(norm.rvs(5, size=500))
5.0098355106969992  # 随机

因此，为了解释上一节的示例输出：norm.rvs(5) 生成一个均值为 loc=5 的正态分布随机变量，因为默认的 size=1。

我们建议您通过传递值作为关键字而不是参数来显式设置 loc 和 scale 参数。当调用给定 RV 的多个方法时，可以通过使用下面解释的冻结分布技术来最小化重复。

形状参数#

虽然一般的连续随机变量可以通过 loc 和 scale 参数进行平移和缩放，但某些分布需要额外的形状参数。例如，具有密度的伽马分布

\[\gamma(x, a) = \frac{\lambda (\lambda x)^{a-1}}{\Gamma(a)} e^{-\lambda x}\;,\]

需要形状参数 \(a\)。请注意，设置 \(\lambda\) 可以通过将 scale 关键字设置为 \(1/\lambda\) 来实现。让我们检查伽玛分布的形状参数的数量和名称。（根据上面的信息，我们知道这应该是1。）

>>> from scipy.stats import gamma
>>> gamma.numargs
1
>>> gamma.shapes
'a'

现在，我们将形状变量的值设置为1以获得指数分布，这样我们可以轻松比较是否得到了预期的结果。

>>> gamma(1, scale=2.).stats(moments="mv")
(array(2.0), array(4.0))

请注意，我们也可以将形状参数指定为关键字：

>>> gamma(a=1, scale=2.).stats(moments="mv")
(array(2.0), array(4.0))

冻结分布#

每次传递 loc 和 scale 关键字可能会变得相当麻烦。使用冻结 RV 的概念来解决这类问题。

>>> rv = gamma(1, scale=2.)

通过使用 rv，我们不再需要包含比例或形状参数。因此，分布可以通过两种方式使用，要么通过将所有分布参数传递给每个方法调用（就像我们之前所做的那样），要么通过冻结分布实例的参数。让我们检查一下：

>>> rv.mean(), rv.std()
(2.0, 2.0)

这确实是我们应该得到的结果。

广播#

基本方法 pdf 等，满足通常的 numpy 广播规则。例如，我们可以计算不同概率和自由度的 t 分布的上尾临界值。

>>> stats.t.isf([0.1, 0.05, 0.01], [[10], [11]])
array([[ 1.37218364,  1.81246112,  2.76376946],
       [ 1.36343032,  1.79588482,  2.71807918]])

这里，第一行包含10个自由度的临界值，第二行包含11个自由度的临界值。因此，广播规则给出了与调用 isf 两次相同的结果：

>>> stats.t.isf([0.1, 0.05, 0.01], 10)
array([ 1.37218364,  1.81246112,  2.76376946])
>>> stats.t.isf([0.1, 0.05, 0.01], 11)
array([ 1.36343032,  1.79588482,  2.71807918])
array([ 1.36343032,  1.79588482,  2.71807918])

如果概率数组，即 [0.1, 0.05, 0.01] 和自由度数组，即 [10, 11, 12]，具有相同的数组形状，则使用元素逐个匹配。例如，我们可以通过调用以下代码来获取10个自由度的10%尾部、11个自由度的5%尾部和12个自由度的1%尾部：

>>> stats.t.isf([0.1, 0.05, 0.01], [10, 11, 12])
array([ 1.37218364,  1.79588482,  2.68099799])

离散分布的特定点#

离散分布的大部分基本方法与连续分布相同。然而，pdf 被概率质量函数 pmf 取代，没有诸如拟合等估计方法可用，并且 scale 不是一个有效的关键字参数。位置参数，关键字 loc，仍然可以用来移动分布。

计算 cdf 需要一些额外的关注。在连续分布的情况下，累积分布函数在大多数标准情况下在边界 (a,b) 内是严格单调递增的，因此具有唯一的逆函数。然而，离散分布的 cdf 是一个阶梯函数，因此逆 cdf，即百分点函数，需要不同的定义：

ppf(q) = min{x : cdf(x) >= q, x 为整数}

更多信息，请参阅文档这里。

我们可以以超几何分布为例

>>> from scipy.stats import hypergeom
>>> [M, n, N] = [20, 7, 12]

如果我们使用 cdf 在一些整数点上，然后在这些 cdf 值上评估 ppf，我们会得到初始的整数，例如

>>> x = np.arange(4) * 2
>>> x
array([0, 2, 4, 6])
>>> prb = hypergeom.cdf(x, M, n, N)
>>> prb
array([  1.03199174e-04,   5.21155831e-02,   6.08359133e-01,
         9.89783282e-01])
>>> hypergeom.ppf(prb, M, n, N)
array([ 0.,  2.,  4.,  6.])

如果我们使用不在cdf阶跃函数拐点处的值，我们会得到下一个更高的整数：

>>> hypergeom.ppf(prb + 1e-8, M, n, N)
array([ 1.,  3.,  5.,  7.])
>>> hypergeom.ppf(prb - 1e-8, M, n, N)
array([ 0.,  2.,  4.,  6.])

拟合分布#

非冻结分布的主要附加方法与分布参数的估计相关：

fit: 分布参数的最大似然估计，包括位置和尺度
fit_loc_scale: 当形状参数已知时，估计位置和尺度
nnlf: 负对数似然函数
expect: 计算函数相对于pdf或pmf的期望值

性能问题和注意事项#

各个方法的性能（以速度衡量）因分布和方法的不同而有很大差异。方法的结果通过以下两种方式之一获得：要么通过显式计算，要么通过独立于特定分布的通用算法。

一方面，显式计算要求该方法直接为给定的分布指定，无论是通过解析公式还是通过``scipy.special``或``numpy.random``中的特殊函数用于``rvs``。这些通常是相对较快的计算。

另一方面，如果分布没有指定任何显式计算，则使用通用方法。要定义一个分布，只需要pdf或cdf中的一个；所有其他方法都可以通过数值积分和求根来推导。然而，这些间接方法可能`非常`慢。例如，``rgh = stats.gausshyper.rvs(0.5, 2, 2, 2, size=100)``以非常间接的方式创建随机变量，在我的计算机上大约需要19秒来生成100个随机变量，而一百万个标准正态分布或t分布的随机变量只需一秒多一点。剩余问题 ^^^^^^^^^^^^^^^^

scipy.stats 中的分布最近得到了修正和改进，并增加了一套相当完善的测试套件；然而，仍有一些问题存在：

这些分布已经在某些参数范围内进行了测试；然而，在一些极端范围内，可能仍存在一些错误结果。
fit 中的最大似然估计在所有分布中并不总是适用于默认的起始参数，用户需要提供良好的起始参数。此外，对于某些分布，使用最大似然估计可能本身就不是最佳选择。

构建特定分布#

接下来的示例展示了如何构建自己的分布。进一步的示例展示了分布的使用以及一些统计测试。

创建一个连续分布，即子类化 `rv_continuous`#

创建连续分布相当简单。

>>> from scipy import stats
>>> class deterministic_gen(stats.rv_continuous):
...     def _cdf(self, x):
...         return np.where(x < 0, 0., 1.)
...     def _stats(self):
...         return 0., 0., 0., 0.

>>> deterministic = deterministic_gen(name="deterministic")
>>> deterministic.cdf(np.arange(-3, 3, 0.5))
array([ 0.,  0.,  0.,  0.,  0.,  0.,  1.,  1.,  1.,  1.,  1.,  1.])

有趣的是，pdf 现在会自动计算：

>>> deterministic.pdf(np.arange(-3, 3, 0.5))
array([  0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
         0.00000000e+00,   0.00000000e+00,   0.00000000e+00,
         5.83333333e+04,   4.16333634e-12,   4.16333634e-12,
         4.16333634e-12,   4.16333634e-12,   4.16333634e-12])

请注意在性能问题和注意事项中提到的一些性能问题。未指定的计算通用方法可能会变得非常慢，因为只能调用一般方法，而这些方法本质上无法利用分布的任何特定信息。因此，作为一个警示性的例子：

>>> from scipy.integrate import quad
>>> quad(deterministic.pdf, -1e-1, 1e-1)
(4.163336342344337e-13, 0.0)

但这并不正确：对这个概率密度函数的积分结果应该是1。让我们缩小积分区间：

>>> quad(deterministic.pdf, -1e-3, 1e-3)  # 警告已移除
(1.000076872229173, 0.0010625571718182458)

这看起来好多了。然而，问题源于在确定性分布的类定义中未指定概率密度函数。

子类化 `rv_discrete`#

接下来，我们使用 stats.rv_discrete 生成一个离散分布，该分布具有以整数为中心的区间的截断正态分布的概率。

一般信息

从 rv_discrete 的文档字符串中，help(stats.rv_discrete)，

“你可以构造一个任意的离散随机变量，其中 P{X=xk} = pk，通过将一个包含序列 (xk, pk) 的元组传递给 rv_discrete 的初始化方法（通过 values= 关键字），该元组仅描述那些以非零概率 (pk) 出现的 X 值 (xk)。”

除此之外，这种方法还有一些额外的要求：

必须提供 name 关键字。
分布的支持点 xk 必须是整数。
需要指定有效数字（小数位数）。

实际上，如果不满足最后两个要求，可能会引发异常或导致结果不正确。

一个示例

让我们开始工作。首先：

>>> npoints = 20   # 分布的整数支持点数减1
>>> npointsh = npoints // 2
>>> npointsf = float(npoints)
>>> nbound = 4   # 截断正态的边界
>>> normbound = (1+1/npointsf) * nbound   # 截断正态的实际边界

>>> grid = np.arange(-npointsh, npointsh+2, 1)   # 整数网格
>>> gridlimitsnorm = (grid-0.5) / npointsh * nbound   # 截断正态分布的分箱边界
>>> gridlimits = grid - 0.5   # 稍后在分析中使用
>>> grid = grid[:-1]
>>> probs = np.diff(stats.truncnorm.cdf(gridlimitsnorm, -normbound, normbound))
>>> gridint = grid

最后，我们可以对 rv_discrete 进行子类化：

>>> normdiscrete = stats.rv_discrete(values=(gridint,
...              np.round(probs, decimals=7)), name='normdiscrete')

现在我们已经定义了分布，我们可以访问离散分布的所有常用方法。

>>> print('mean = %6.4f, variance = %6.4f, skew = %6.4f, kurtosis = %6.4f' %
...       normdiscrete.stats(moments='mvsk'))
mean = -0.0000, variance = 6.3302, skew = 0.0000, kurtosis = -0.0076

>>> nd_std = np.sqrt(normdiscrete.stats(moments='v'))

测试实现

让我们生成一个随机样本，并将观察到的频率与概率进行比较。

>>> n_sample = 500
>>> rvs = normdiscrete.rvs(size=n_sample)
>>> f, l = np.histogram(rvs, bins=gridlimits)
>>> sfreq = np.vstack([gridint, f, probs*n_sample]).T
>>> print(sfreq)
[[-1.00000000e+01  0.00000000e+00  2.95019349e-02]  # 随机
 [-9.00000000e+00  0.00000000e+00  1.32294142e-01]
 [-8.00000000e+00  0.00000000e+00  5.06497902e-01]
 [-7.00000000e+00  2.00000000e+00  1.65568919e+00]
 [-6.00000000e+00  1.00000000e+00  4.62125309e+00]
 [-5.00000000e+00  9.00000000e+00  1.10137298e+01]
 [-4.00000000e+00  2.60000000e+01  2.24137683e+01]
 [-3.00000000e+00  3.70000000e+01  3.89503370e+01]
 [-2.00000000e+00  5.10000000e+01  5.78004747e+01]
 [-1.00000000e+00  7.10000000e+01  7.32455414e+01]
 [ 0.00000000e+00  7.40000000e+01  7.92618251e+01]
 [ 1.00000000e+00  8.90000000e+01  7.32455414e+01]
 [ 2.00000000e+00  5.50000000e+01  5.78004747e+01]

[ 3.00000000e+00 5.00000000e+01 3.89503370e+01] [ 4.00000000e+00 1.70000000e+01 2.24137683e+01] [ 5.00000000e+00 1.10000000e+01 1.10137298e+01] [ 6.00000000e+00 4.00000000e+00 4.62125309e+00] [ 7.00000000e+00 3.00000000e+00 1.65568919e+00] [ 8.00000000e+00 0.00000000e+00 5.06497902e-01] [ 9.00000000e+00 0.00000000e+00 1.32294142e-01] [ 1.00000000e+01 0.00000000e+00 2.95019349e-02]]

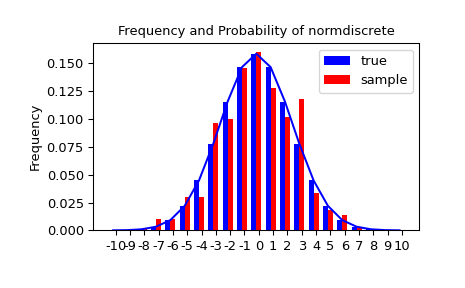
"一个X-Y直方图，显示随机变量的分布。一条蓝色曲线显示了正态钟形曲线。一个蓝色条形图完美地近似了曲线，显示了真实的分布。一个代表样本的红色条形图很好地被蓝色曲线描述，但并不完全精确。"

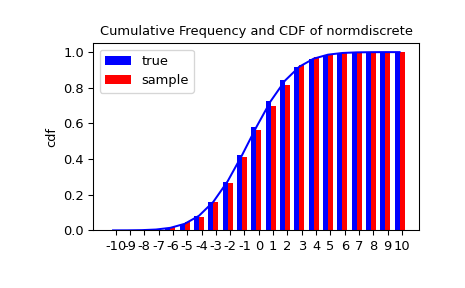
"一个X-Y直方图，显示随机变量的累积分布。一条蓝色曲线显示了典型正态分布的CDF。一个蓝色条形图完美地近似了曲线，显示了真实的分布。一个代表样本的红色条形图很好地被蓝色曲线描述，但并不完全精确。"

接下来，我们可以测试我们的样本是否由我们的norm-discrete分布生成。这也验证了随机数是否正确生成。

卡方检验要求每个箱子中有足够数量的观测值。我们将尾部箱子合并成更大的箱子，以便它们包含足够的观测值。

>>> f2 = np.hstack([f[:5].sum(), f[5:-5], f[-5:].sum()])
>>> p2 = np.hstack([probs[:5].sum(), probs[5:-5], probs[-5:].sum()])
>>> ch2, pval = stats.chisquare(f2, p2*n_sample)

>>> print('normdiscrete的卡方检验: chi2 = %6.3f pvalue = %6.4f' % (ch2, pval))
normdiscrete的卡方检验: chi2 = 12.466 pvalue = 0.4090  # 随机

在这种情况下，p值较高，因此我们可以相当有信心地认为我们的随机样本实际上是由该分布生成的。