准蒙特卡罗方法#

在谈论准蒙特卡罗方法（QMC）之前，先简要介绍一下蒙特卡罗方法（MC）。MC方法，或称MC实验，是一类广泛的计算算法，依赖于重复的随机抽样来获得数值结果。其基本概念是利用随机性来解决原则上可能是确定性的问题。它们通常用于物理和数学问题，并且在难以或不可能使用其他方法时最为有用。MC方法主要用于三类问题：优化、数值积分和生成概率分布的抽样。

生成具有特定属性的随机数比听起来要复杂得多。简单的MC方法旨在对独立同分布（IID）的点进行抽样。但生成多组随机点可能会产生截然不同的结果。

" "

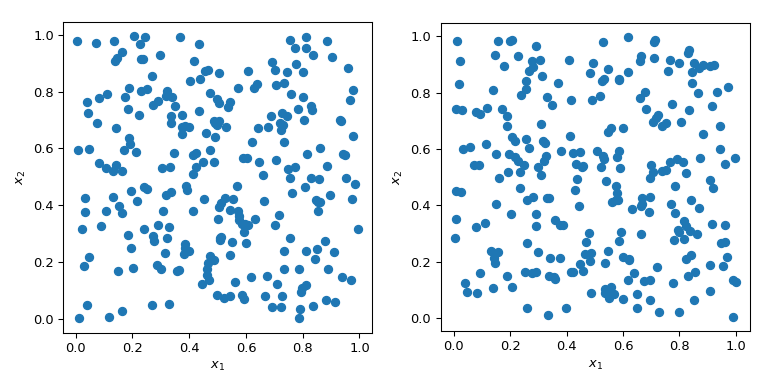
在上图的两种情况下，点都是随机生成的，没有任何关于先前绘制点的信息。很明显，空间中的某些区域未被探索——这可能会在模拟中引发问题，因为特定的一组点可能会触发完全不同的行为。

MC的一个巨大优势是它具有已知的收敛性质。让我们看一下5维中平方和的均值：

\[f(\mathbf{x}) = \left( \sum_{j=1}^{5}x_j \right)^2,\]

其中 \(x_j \sim \mathcal{U}(0,1)\)。它有一个已知的均值，\(\mu = 5/3+5(5-1)/4\)。使用MC抽样，我们可以数值计算该均值，并且近似误差遵循理论速率 \(O(n^{-1/2})\)。

" "

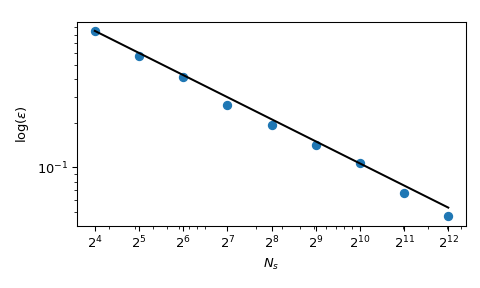
尽管收敛性得到了保证，但从业者往往希望更快地获得结果。 探索过程更具确定性。使用普通的蒙特卡罗方法时，可以通过设置种子来实现可重复的过程。但固定种子会破坏收敛性：给定的种子可能适用于某一类问题，而对另一类问题则失效。

通常为了以确定性的方式遍历空间，会使用一个覆盖所有参数维度的规则网格，也称为饱和设计。我们考虑单位超立方体，其所有边界范围从0到1。现在，如果点之间的距离为0.1，填充单位区间所需点的数量为10。在二维超立方体中，相同的间距需要100个点，而在三维空间中需要1,000个点。随着维度的增加，填充空间所需实验的数量呈指数增长。这种指数增长被称为“维数灾难”。

>>> import numpy as np
>>> disc = 10
>>> x1 = np.linspace(0, 1, disc)
>>> x2 = np.linspace(0, 1, disc)
>>> x3 = np.linspace(0, 1, disc)
>>> x1, x2, x3 = np.meshgrid(x1, x2, x3)
" "

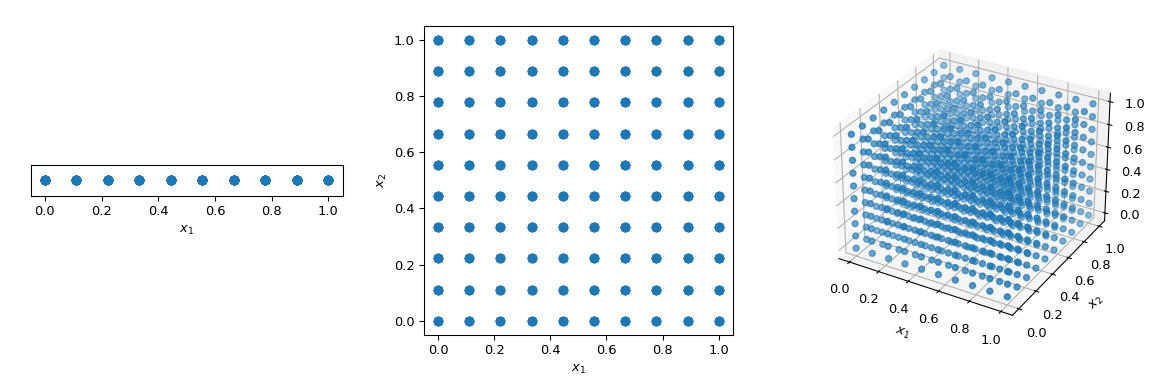
为了缓解这个问题，设计了准蒙特卡罗（QMC）方法。它们是确定性的，能够很好地覆盖空间，并且其中一些方法可以继续进行并保持良好的性质。与蒙特卡罗方法的主要区别在于，点不是独立同分布的，而是知道先前的点。因此，一些方法也被称为序列。

" "

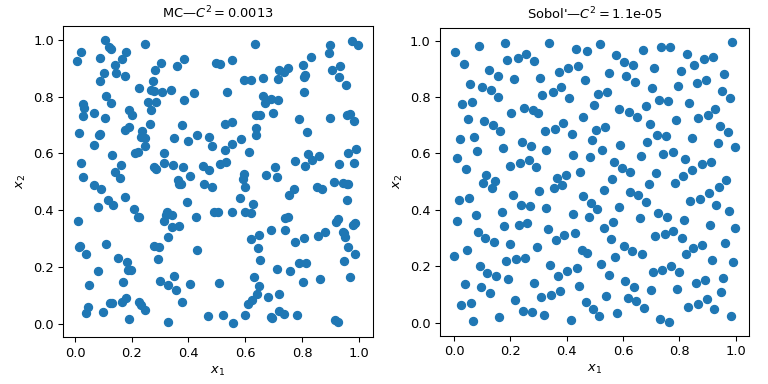
这幅图展示了2组256个点。左边的设计是普通的蒙特卡罗方法，而右边的设计是使用*Sobol’方法的QMC设计。我们可以清楚地看到，QMC版本更加均匀。点在边界附近更好地采样，并且聚类或间隙更少。 评估均匀性的一种方法是使用称为偏差（discrepancy）的度量。这里，*Sobol’ 点的偏差优于粗略蒙特卡罗（crude MC）。

回到均值的计算，准蒙特卡罗（QMC）方法在误差收敛率方面也表现更好。对于这个函数，它们可以达到 \(O(n^{-1})\)，甚至在非常光滑的函数上可以达到更好的收敛率。下图显示了 Sobol’ 方法的收敛率为 \(O(n^{-1})\)：

" "

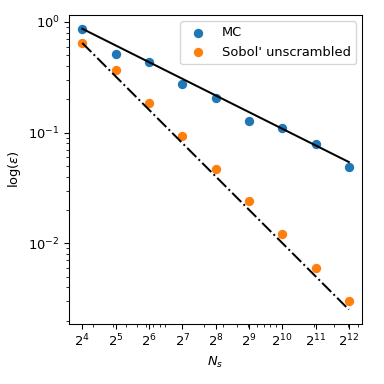
我们参考 scipy.stats.qmc 的文档以获取更多数学细节。

计算偏差#

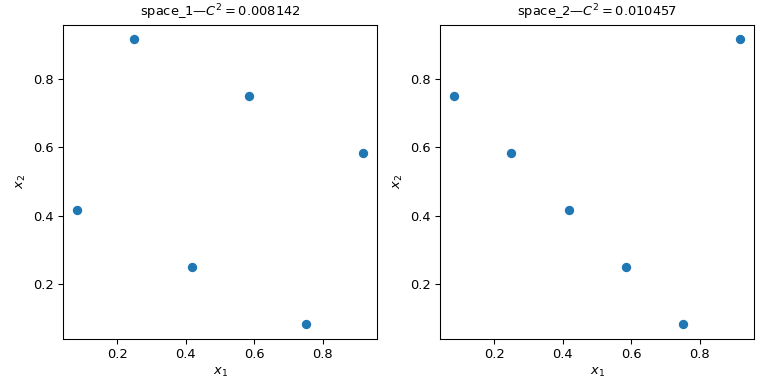
让我们考虑两组点。从下图可以清楚地看出，左侧的设计比右侧的设计覆盖了更多的空间。这可以使用 scipy.stats.qmc.discrepancy 度量来量化。偏差越低，样本越均匀。

>>> import numpy as np
>>> from scipy.stats import qmc
>>> space_1 = np.array([[1, 3], [2, 6], [3, 2], [4, 5], [5, 1], [6, 4]])
>>> space_2 = np.array([[1, 5], [2, 4], [3, 3], [4, 2], [5, 1], [6, 6]])
>>> l_bounds = [0.5, 0.5]
>>> u_bounds = [6.5, 6.5]
>>> space_1 = qmc.scale(space_1, l_bounds, u_bounds, reverse=True)
>>> space_2 = qmc.scale(space_2, l_bounds, u_bounds, reverse=True)
>>> qmc.discrepancy(space_1)
0.008142039609053464
>>> qmc.discrepancy(space_2)
0.010456854423869011
" "

使用 QMC 引擎#

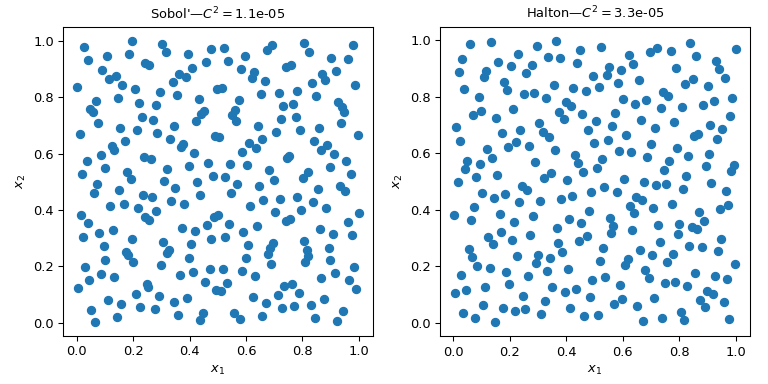
实现了几种 QMC 采样器/引擎。这里我们来看两种最常用的 QMC 方法：scipy.stats.qmc.Sobol 和 scipy.stats.qmc.Halton 序列。

"""Sobol' and Halton sequences."""
from scipy.stats import qmc
import numpy as np

import matplotlib.pyplot as plt


rng = np.random.default_rng()

n_sample = 256
dim = 2

sample = {}

# Sobol'
engine = qmc.Sobol(d=dim, seed=rng)
sample["Sobol'"] = engine.random(n_sample)

# Halton
engine = qmc.Halton(d=dim, seed=rng)
sample["Halton"] = engine.random(n_sample)

fig, axs = plt.subplots(1, 2, figsize=(8, 4))

for i, kind in enumerate(sample):
    axs[i].scatter(sample[kind][:, 0], sample[kind][:, 1])

    axs[i].set_aspect('equal')
    axs[i].set_xlabel(r'$x_1$')
    axs[i].set_ylabel(r'$x_2$')
    axs[i].set_title(f'{kind}—$C^2 = ${qmc.discrepancy(sample[kind]):.2}')

plt.tight_layout()
plt.show()
" "

警告

QMC方法需要特别小心，用户必须阅读文档以避免常见陷阱。例如，*Sobol’*要求点的数量遵循2的幂次。此外，抽取、燃烧或其他点选择可能会破坏序列的性质，导致生成的点集不如MC方法。

QMC引擎具有状态感知能力。这意味着你可以继续序列、跳过一些点或重置它。让我们从:class:`scipy.stats.qmc.Halton`中取5个点。然后请求第二组5个点：

>>> from scipy.stats import qmc
>>> engine = qmc.Halton(d=2)
>>> engine.random(5)
array([[0.22166437, 0.07980522],  # random
       [0.72166437, 0.93165708],
       [0.47166437, 0.41313856],
       [0.97166437, 0.19091633],
       [0.01853937, 0.74647189]])
>>> engine.random(5)
array([[0.51853937, 0.52424967],  # random
       [0.26853937, 0.30202745],
       [0.76853937, 0.857583  ],
       [0.14353937, 0.63536078],
       [0.64353937, 0.01807683]])

现在我们重置序列。请求5个点会得到相同的前5个点：

>>> engine.reset()
>>> engine.random(5)
array([[0.22166437, 0.07980522],  # random
       [0.72166437, 0.93165708],
       [0.47166437, 0.41313856],
       [0.97166437, 0.19091633],
       [0.01853937, 0.74647189]])

然后我们推进序列以获取相同的第二组5个点：

>>> engine.reset()
>>> engine.fast_forward(5)
>>> engine.random(5)
array([[0.51853937, 0.52424967],  # random
       [0.26853937, 0.30202745],
       [0.76853937, 0.857583  ],
       [0.14353937, 0.63536078],
       [0.64353937, 0.01807683]])

备注

默认情况下，:class:`scipy.stats.qmc.Sobol`和:class:`scipy.stats.qmc.Halton`都会进行扰动。这会改善收敛性，并防止出现条纹或明显的模式。

高维中的点分布。没有实际理由不使用打乱版本。

制作一个QMC引擎，即子类化 QMCEngine#

要制作你自己的 scipy.stats.qmc.QMCEngine，必须定义一些方法。以下是一个包装 numpy.random.Generator 的示例。

>>> import numpy as np
>>> from scipy.stats import qmc
>>> class RandomEngine(qmc.QMCEngine):
...     def __init__(self, d, seed=None):
...         super().__init__(d=d, seed=seed)
...         self.rng = np.random.default_rng(self.rng_seed)
...
...
...     def _random(self, n=1, *, workers=1):
...         return self.rng.random((n, self.d))
...
...
...     def reset(self):
...         self.rng = np.random.default_rng(self.rng_seed)
...         self.num_generated = 0
...         return self
...
...
...     def fast_forward(self, n):
...         self.random(n)
...         return self

然后我们像使用其他QMC引擎一样使用它：

>>> engine = RandomEngine(2)
>>> engine.random(5)
array([[0.22733602, 0.31675834],  # 随机
       [0.79736546, 0.67625467],
       [0.39110955, 0.33281393],
       [0.59830875, 0.18673419],
       [0.67275604, 0.94180287]])
>>> engine.reset()
>>> engine.random(5)
array([[0.22733602, 0.31675834],  # 随机
       [0.79736546, 0.67625467],
       [0.39110955, 0.33281393],
       [0.59830875, 0.18673419],
       [0.67275604, 0.94180287]])

使用QMC的指南#

  • QMC有规则！务必阅读文档，否则你可能无法获得比MC更好的效果。

  • 如果你需要**恰好** \(2^m\) 个点，请使用 scipy.stats.qmc.Sobol。

  • scipy.stats.qmc.Halton 允许采样或跳过任意数量的点。这会以比 Sobol’ 更慢的收敛速度为代价。

  • 切勿移除序列的第一个点。这将破坏其性质。

  • 打乱顺序总是更好的选择。

  • 如果你使用基于LHS的方法，添加点会导致失去LHS的性质。（有一些方法可以做到这一点，但目前尚未实现。）

On this page