简单比率均匀法 (SROU)#
必需:PDF,如果与1不同,则为PDF下的面积
可选:众数,众数处的CDF
速度:
设置:快速
采样:慢速
SROU基于比率均匀法,该方法使用通用不等式来构建一个(通用)边界矩形。它适用于T-凹分布,其中T(x) = -1/sqrt(x)。
>>> import numpy as np
>>> from scipy.stats.sampling import SimpleRatioUniforms
假设我们有一个标准正态分布:
>>> class StdNorm:
... def pdf(self, x):
... return np.exp(-0.5 * x**2)
注意,PDF的积分不等于1。我们可以在生成器的初始化过程中传递PDF下的确切面积或PDF下面积的上限。此外,建议传递分布的众数以加快设置速度:
>>> urng = np.random.default_rng()
>>> dist = StdNorm()
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... random_state=urng)
现在,我们可以使用 rvs 方法从分布中生成样本:
>>> rvs = rng.rvs(10)
如果众数处的CDF可用,可以设置它以提高 rvs 的性能:
>>> from scipy.stats import norm
>>> rng = SimpleRatioUniforms(dist, mode=0,
... pdf_area=np.sqrt(2*np.pi),
... cdf_at_mode=norm.cdf(0),
... random_state=urng)
>>> rvs = rng.rvs(1000)
我们可以通过可视化其直方图来检查样本是否来自给定的分布:
>>> from scipy.stats.sampling import SimpleRatioUniforms
>>> from scipy.stats import norm
>>> import matplotlib.pyplot as plt
>>> class StdNorm:
... def pdf(self, x):
... return np.exp(-0.5 * x**2)
… >>> urng = np.random.default_rng() >>> dist = StdNorm() >>> rng = SimpleRatioUniforms(dist, mode=0, … pdf_area=np.sqrt(2*np.pi), … cdf_at_mode=norm.cdf(0), … random_state=urng) >>> rvs = rng.rvs(1000) >>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000) >>> fx = 1/np.sqrt(2*np.pi) * dist.pdf(x) >>> fig, ax = plt.subplots() >>> ax.plot(x, fx, ‘r-’, lw=2, label=’真实分布’) >>> ax.hist(rvs, bins=10, density=True, alpha=0.8, label=’随机变量’) >>> ax.set_xlabel(‘x’) >>> ax.set_ylabel(‘PDF(x)’) >>> ax.set_title(‘简单比率均匀样本’) >>> ax.legend() >>> plt.show()
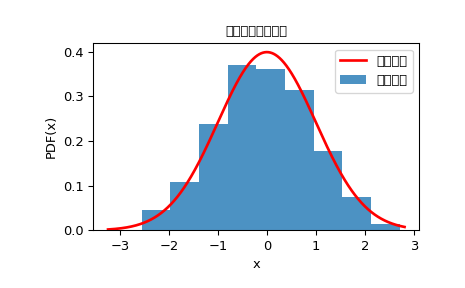
该方法的主要优势在于快速设置。如果需要反复生成具有不同形状参数的分布的小到中等样本,这将非常有利。在这种情况下,sampling.NumericalInverseHermite 或 sampling.NumericalInversePolynomial 的设置步骤会导致性能不佳。例如,假设我们对生成100个Gamma分布样本感兴趣,其形状参数为 np.arange(1.5, 5, 1000) 中的1000个不同值。
>>> import math
>>> class GammaDist:
... def __init__(self, p):
... self.p = p
... def pdf(self, x):
... return x**(self.p-1) * np.exp(-x)
...
>>> urng = np.random.default_rng()
>>> p = np.arange(1.5, 5, 1000)
>>> res = np.empty((1000, 100))
>>> for i in range(1000):
... dist = GammaDist(p[i])
... rng = SimpleRatioUniforms(dist, mode=p[i]-1,
... pdf_area=math.gamma(p[i]),
... random_state=urng)
... with np.testing.suppress_warnings() as sup:
... sup.filter(RuntimeWarning, "invalid value encountered in double_scalars")
... sup.filter(RuntimeWarning, "overflow encountered in exp")
... res[i] = rng.rvs(100)
更多详情请参见[1]_、[2]_和[3]_。