括号对颜色化速度提升10,000倍

2021年9月29日，由Henning Dieterichs发布，@hediet_dev

在Visual Studio Code中处理深度嵌套的括号时，可能很难确定哪些括号匹配，哪些不匹配。

为了简化这一过程，2016年，一位名为CoenraadS的用户开发了令人惊叹的Bracket Pair Colorizer扩展，用于为匹配的括号着色，并将其发布到VS Code市场。这个扩展变得非常流行，现在是市场上最受欢迎的10个扩展之一，安装量超过600万。

为了解决性能和准确性问题，2018年，CoenraadS 推出了 Bracket Pair Colorizer 2，该插件现在也有超过300万的安装量。

Bracket Pair Colorizer 扩展是 VS Code 可扩展性的一个很好的例子，它大量使用了 Decoration API 来为括号着色。

在VS Code中打开的相同代码的两个截图。第一张截图中，括号对颜色化功能被禁用，第二张截图中，该功能被启用

我们很高兴看到VS Code市场提供了更多这样的社区提供的扩展，所有这些扩展都以非常有创意的方式帮助识别匹配的括号对，包括：Rainbow Brackets, Subtle Match Brackets, Bracket Highlighter, Blockman, 和 Bracket Lens。这些多样化的扩展表明，VS Code用户确实希望获得更好的括号支持。

性能问题

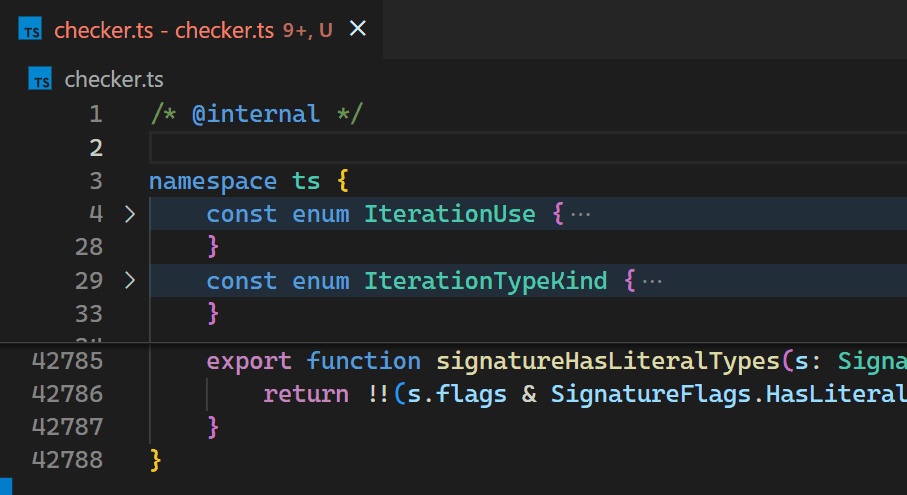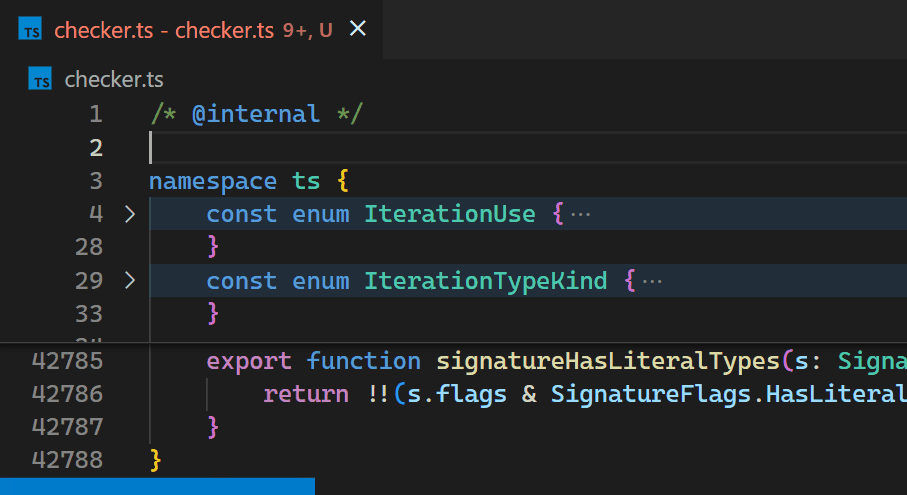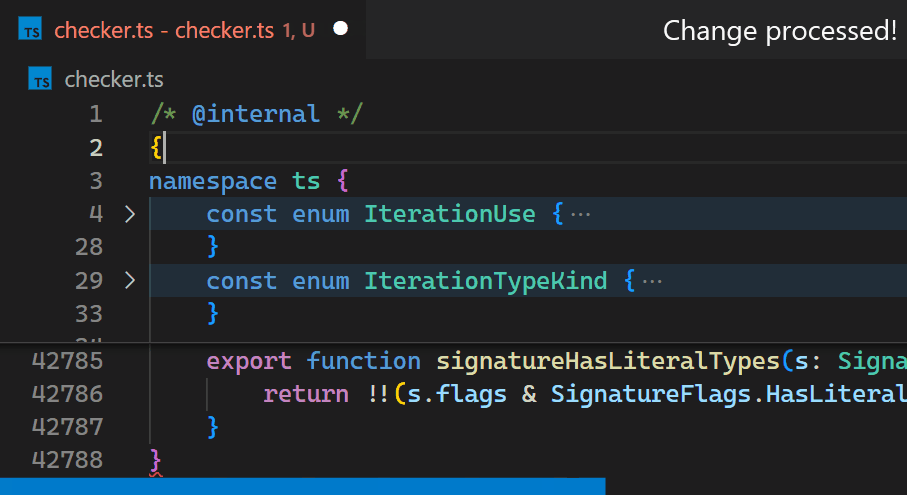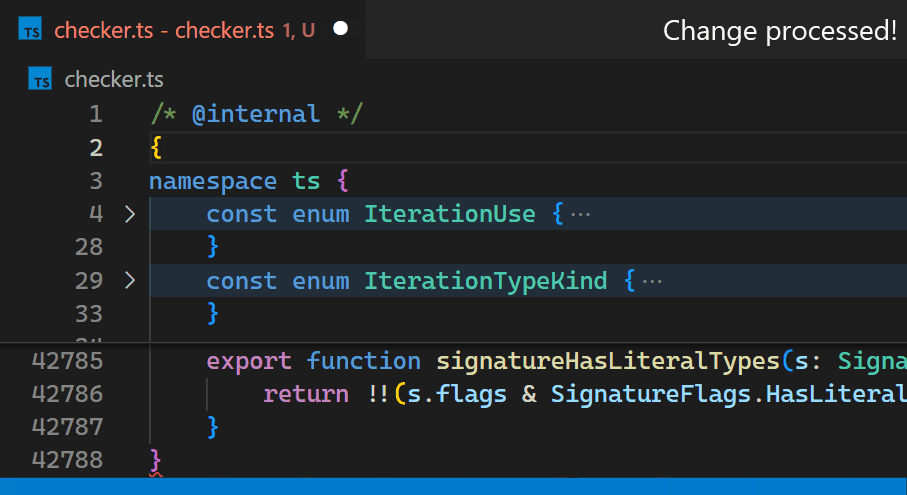
不幸的是，由于Decoration API的非增量性质以及无法访问VS Code的标记信息，导致Bracket Pair Colorizer扩展在大型文件上运行缓慢：在TypeScript项目的checker.ts文件的开头插入一个括号时，该文件有超过42k行代码，大约需要10秒钟才能更新所有括号对的颜色。在这10秒的处理过程中，扩展主机进程的CPU使用率达到100%，所有由扩展支持的功能，如自动完成或诊断，都会停止工作。幸运的是，VS Code的架构确保了UI保持响应，并且文档仍然可以保存到磁盘。

CoenraadS意识到了这个性能问题，并在扩展的第2版中投入了大量精力来提高速度和准确性，通过重用VS Code的标记和括号解析引擎。然而，VS Code的API和扩展架构并未设计为在涉及数十万个括号对时允许高性能的括号对着色。因此，即使在Bracket Pair Colorizer 2中，在文件开头插入{后，颜色反映新的嵌套级别也需要一些时间：

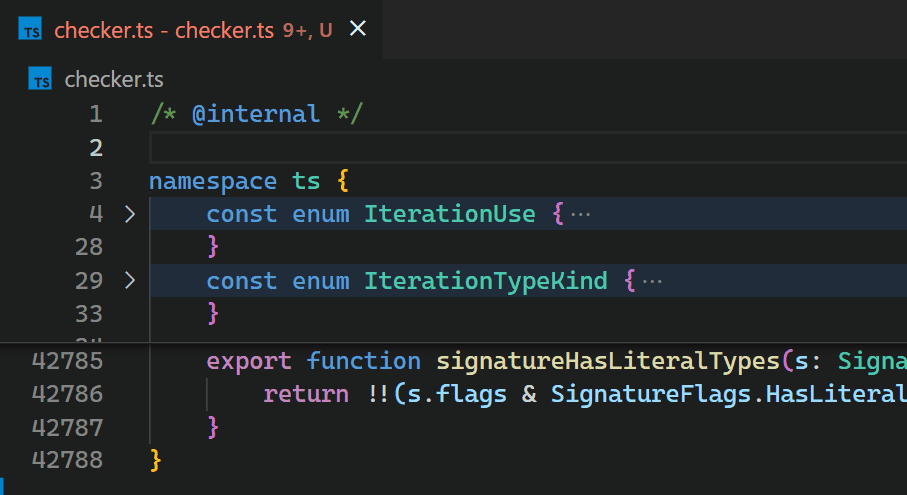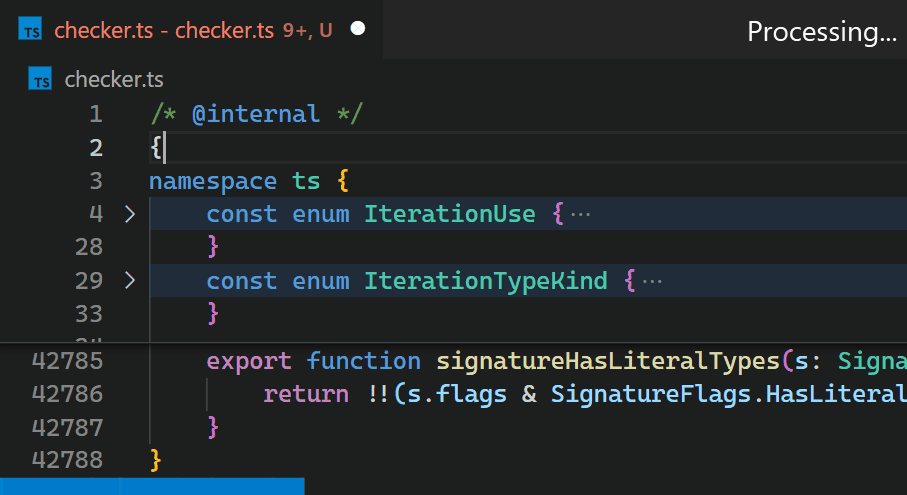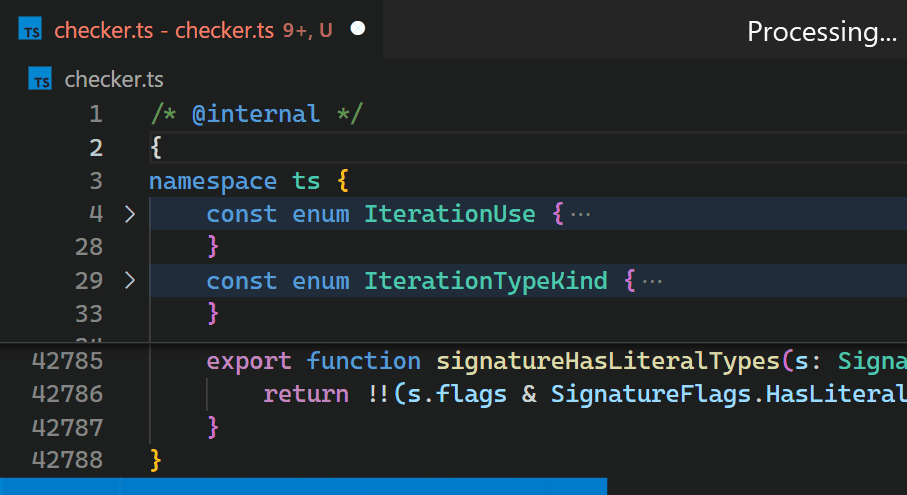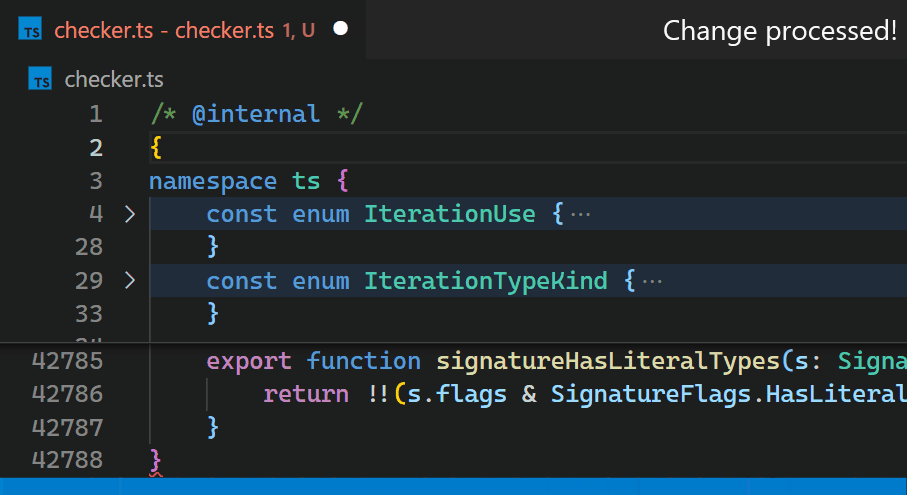
一段VS Code视频显示扩展需要超过10秒来处理checker.ts中的文本更改

虽然我们非常希望仅仅提高扩展的性能（这肯定需要引入更多高级API，针对高性能场景进行优化），但渲染器和扩展主机之间的异步通信严重限制了当括号对颜色化作为扩展实现时的速度。这个限制是无法克服的。特别是，括号对颜色不应该在它们出现在视口中时异步请求，因为这在滚动大文件时会导致可见的闪烁。关于这一点的讨论可以在issue #128465中找到。

我们做了什么

相反，在1.60更新中，我们在VS Code的核心中重新实现了该扩展，并将时间缩短到不到一毫秒——在这个特定的例子中，这比之前快了10,000多倍。

可以通过添加设置"editor.bracketPairColorization.enabled": true来启用该功能。

现在，即使对于包含数十万个大括号对的文件，更新也不再明显。请注意，在第42,788行的大括号颜色在输入第2行的{后立即反映了新的嵌套级别：

一段VS Code视频，展示了原生实现在处理checker.ts中的文本更改时所需时间不到一毫秒

一旦我们决定将其移入核心，我们也借此机会研究了如何使其尽可能快。谁会不喜欢一个算法挑战呢？

不受公共API设计的限制，我们可以使用(2,3)-树、无递归树遍历、位运算、增量解析等技术来减少扩展的最坏情况更新时间复杂度（即在文档已经打开时处理用户输入所需的时间）从 $\mathcal{O}(N + E)$ 到 $\mathcal{O}(\mathrm{log}^3 N + E)$ ，其中 $N$ 是文档大小， $E$ 是编辑大小，假设括号对的嵌套级别由 $\mathcal{O}(\mathrm{log} N)$ 限制。

此外，通过重用渲染器中的现有令牌及其增量令牌更新机制，我们获得了另一个巨大的（但恒定的）加速。

网页版VS Code

除了性能更好之外，新的实现还在VS Code for the Web中得到支持，您可以在vscode.dev和github.dev中看到它的实际应用。由于Bracket Pair Colorizer 2重用VS Code标记引擎的方式，无法将该扩展迁移为我们所称的web extension。

我们的新实现不仅在VS Code网页版中有效，而且直接在Monaco Editor中也有效！

括号对颜色化的挑战

括号对颜色化主要是关于快速确定视口中所有括号及其（绝对）嵌套级别。视口可以描述为文档中行号和列号范围内的一个区域，通常是整个文档的一小部分。

不幸的是，括号的嵌套级别取决于它前面的所有字符：将任何字符替换为开括号“{”通常会增加所有后续括号的嵌套级别。

因此，当最初在文档的最末尾对括号进行着色时，必须处理整个文档的每一个字符。

一张图表，表明更改单个字符会影响所有后续括号的嵌套级别

括号对颜色化扩展中的实现通过在处理整个文档时再次处理整个文档来解决这个挑战，每当插入或删除一个括号时（这对于小文档来说是非常合理的）。然后必须使用VS Code的Decoration API移除并重新应用颜色，该API将所有颜色装饰发送到渲染器。

如前所述，对于包含数十万个大括号对以及同样多的颜色装饰的大型文档来说，这很慢。因为扩展不能逐步更新装饰，而必须一次性替换所有装饰，所以括号对颜色化扩展甚至无法做得更好。尽管如此，渲染器以一种聪明的方式组织所有这些装饰（通过使用所谓的区间树），因此在接收到（可能数十万个）装饰后，渲染总是很快。

我们的目标不是每次按键时都要重新处理整个文档。相反，处理单个文本编辑所需的时间应该只随着文档长度的增加而（poly）对数增长。

然而，我们仍然希望能够在对数（多对数）时间内查询视口中所有括号及其嵌套级别，就像使用VS Code的装饰API（使用上述的区间树）时的情况一样。

算法复杂度

可以随意跳过关于算法复杂度的部分。

在以下内容中， $N$ 指的是文档的长度。更正式地说，我们的目标是使时间复杂度最多为 $\mathcal{O}(\mathrm{log}^k N + R)$ 用于查询给定大小 $R$ 范围内的所有括号，并且 $k$ 是一个合理的小值（我们的目标是 $k = 2$ ）。括号在渲染视口时被查询，因此查询它们必须非常快。

然而，我们允许在文档首次打开时有一个初始化时间复杂度为 $\mathcal{O}(N)$ （这是不可避免的，因为在最初为括号着色时必须处理所有字符），并且在修改或插入 $E$ 多个字符时，更新时间为 $\mathcal{O}(\mathrm{log}^j N + E)$ ，再次对于一个合理的较小的 $j$ （我们的目标是 $j = 3$ ）。我们还假设括号对的嵌套级别不会太深，最多为 $\mathcal{O}(\mathrm{log} N)$ ，并且没有对应开括号的闭括号数量可以忽略不计——违反这些假设的文档是非典型的，我们寻找的算法不需要在它们上快速运行。

语言语义使得括号对颜色化变得困难

使括号对颜色化真正困难的是检测由文档语言定义的实际括号。特别是，我们不想在注释或字符串中检测到开括号或闭括号，如下面的C示例所示：

{ /* } */ char str[] = "}"; }

只有第三次出现的“}”会关闭括号对。

对于标记语言不是正则的语言，如带有JSX的TypeScript，这变得更加困难：

TypeScript代码的截图，显示了一个包含带有嵌套表达式的模板字面量的函数。模板字面量在位置2还包含一个闭合括号。函数从位置1的括号开始，到位置3的括号结束。

[1]处的括号是与[2]处的括号匹配还是与[3]处的括号匹配？这取决于模板文字表达式的长度，只有具有无限状态的标记器（即非正则标记器）才能正确确定。

令牌来救援

幸运的是，语法高亮必须解决一个类似的问题：在前面的代码片段中，[2]处的括号应该被渲染为字符串还是纯文本？

事实证明，对于大多数括号对来说，只需忽略由语法高亮标识的注释和字符串中的括号就足够了。 < ... > 是我们迄今为止发现的唯一有问题的对，因为这些括号通常既用于比较，也用作泛型类型的对，同时具有相同的标记类型。

VS Code 已经拥有一个高效且同步的机制来维护用于语法高亮的标记信息，我们可以重用该机制来识别开括号和闭括号。

这是Bracket Pair Colorization扩展的另一个挑战，它对性能产生了负面影响：它无法访问这些令牌，必须自行重新计算。我们长时间思考如何能够高效且可靠地向扩展暴露令牌信息，但得出的结论是，如果不让大量实现细节泄露到扩展API中，我们无法做到这一点。因为扩展仍然需要为文档中的每个括号发送颜色装饰列表，仅凭这样的API甚至无法解决性能问题。

顺便提一下，当在文档的开头应用一个编辑操作，该操作会改变所有后续的标记（例如在类似C语言中插入/*），VS Code不会一次性重新标记整个长文档，而是分块逐步进行。这确保了即使标记化在渲染器中同步进行，UI也不会冻结。

基本算法

核心思想是使用递归下降解析器来构建一个抽象语法树（AST），该树描述了所有括号对的结构。当找到一个括号时，检查标记信息，如果它在注释或字符串中，则跳过该括号。标记器允许解析器查看和读取此类括号或文本标记。

现在的技巧是只存储每个节点的长度（并且为所有不是括号的内容创建文本节点以覆盖间隙），而不是存储绝对的开始/结束位置。仅使用长度，仍然可以在AST中高效地定位给定位置的括号节点。

下图展示了一个带有长度注释的示例AST：

具有相对长度的括号对的抽象语法树

将其与使用绝对开始/结束位置的经典AST表示进行比较：

带有绝对开始/结束位置的括号对的抽象语法树

两个AST描述了相同的文档，但在遍历第一个AST时，绝对位置必须即时计算（这样做成本较低），而在第二个AST中，它们已经预先计算好了。

然而，当向第一棵树插入单个字符时，只需更新节点本身及其所有父节点的长度——所有其他长度保持不变。

当绝对位置像第二棵树那样存储时，文档中每个节点的位置都必须递增。

此外，通过不存储绝对偏移量，可以共享具有相同长度的叶节点以避免分配。

这是如何在TypeScript中定义带有长度注释的AST：

type Length = ...;

type AST = BracketAST | BracketPairAST | ListAST | TextAST;

/** Describes a single bracket, such as `{`, `}` or `begin` */
class BracketAST {
    constructor(public length: Length) {}
}

/** Describes a matching bracket pair and the node in between, e.g. `{...}` */
class BracketPairAST {
    constructor(
        public openingBracket: BracketAST;
        public child: BracketPairAST | ListAST | TextAST;
        public closingBracket: BracketAST;
    ) {}

    length = openingBracket.length + child.length + closingBracket.length;
}

/** Describes a list of bracket pairs or text nodes, e.g. `()...()` */
class ListAST {
    constructor(
        public items: Array<BracketPairAST | TextAST>
    ) {}

    length = items.sum(item => item.length);
}

/** Describes text that has no brackets in it. */
class TextAST {
    constructor(public length: Length) {}
}

查询这样的AST以列出视口中所有括号及其嵌套级别相对简单：进行深度优先遍历，动态计算当前节点的绝对位置（通过添加先前节点的长度），并跳过完全在请求范围之前或之后的节点的子节点。

这个基本算法已经可以工作，但还有一些未解决的问题：

我们如何确保在给定范围内查询所有括号具有所需的对数性能？
在输入时，我们如何避免从头开始构建一个新的AST？
我们如何处理令牌块的更新？当打开一个大文档时，令牌最初不可用，但会逐块到来。

确保查询时间为对数时间

在查询给定范围内的括号时，真正影响性能的是非常长的列表：我们无法对其子节点进行快速的二分搜索以跳过所有不相关的非交叉节点，因为我们需要动态计算每个节点的长度以计算绝对位置。在最坏的情况下，我们需要遍历所有节点。

在下面的例子中，我们必须查看13个节点（蓝色）直到我们找到位置24的括号：

抽象语法树中的长列表

虽然我们可以计算并缓存长度总和以启用二分搜索，但这与存储绝对位置有相同的问题：每次单个节点增长或缩小时，我们都需要重新计算所有这些，这对于非常长的列表来说代价很高。

相反，我们允许列表将其他列表作为子项：

class ListAST {
  constructor(public items: Array<ListAST | BracketPairAST | TextAST>) {}

  length = items.sum(item => item.length);
}

这如何改善情况？

如果我们能确保每个列表只有有限数量的子节点，并且类似于对数高度的平衡树，那么事实证明，这对于查询括号获得所需的对数性能是足够的。

保持列表树的平衡

我们使用(2,3)-trees来确保这些列表是平衡的：每个列表必须至少有2个且最多有3个子节点，并且列表的所有子节点在平衡列表树中必须具有相同的高度。请注意，在平衡树中，括号对被视为高度为0的叶子，但它可能在AST中有子节点。

在初始化期间从头开始构建AST时，我们首先收集所有子节点，然后将它们转换为这样的平衡树。这可以在线性时间内完成。

之前示例的一个可能的(2,3)-树可能如下所示。请注意，我们现在只需要查看8个节点（蓝色）来找到位置24的括号对，并且列表有2个还是3个子节点有一定的自由度：

用于描述AST中列表的平衡树

最坏情况复杂度分析

可以随意跳过关于算法复杂度的部分。

目前，我们假设每个列表都类似于一个(2,3)-树，因此最多有3个子节点。

为了最大化查询时间，我们来看一个具有 $\mathcal{O}(\mathrm{log} N)$ 多个嵌套括号对的文档：

{
    {
        ... O(log N) many nested bracket pairs
            {
                {} [1]
            }
        ...
    }
}

尚未涉及列表，但我们已经需要遍历 $\mathcal{O}(\mathrm{log} N)$ 多个节点以找到 [1] 处的括号对。幸运的是，嵌套更深的文档并不典型，因此我们在最坏情况分析中不考虑它们。

现在，对于最坏的情况，我们通过在每个嵌套的括号对中插入额外的 $\mathcal{O}(\frac{N}{\mathrm{log} N})$ 多个括号对，直到文档的大小达到 $N$ ：

{}{}{}{}{}{}{}{}... O(N / log N) many
{
    {}{}{}{}{}{}{}{}... O(N / log N) many
    {
        ... O(log N) many nested bracket pairs
            {
                {}{}{}{}{}{}{}{}... O(N / log N) many
                {} [1]
            }
        ...
    }
}

在同一嵌套级别上的每个括号列表都会生成一个高度为 $\mathcal{O}(\mathrm{log} \frac{N}{\mathrm{log} N}) = \mathcal{O}(\mathrm{log} N - \mathrm{log}\;\mathrm{log} N ) = \mathcal{O}(\mathrm{log} N)$ 的树。

因此，要找到[1]处的节点，我们必须遍历高度为 $\mathcal{O}(\mathrm{log} N)$ 的许多平衡树。一旦我们找到该节点并想要收集大小为 $R$ 的范围内的所有括号，我们必须读取最多 $\mathcal{O}(R)$ 个相邻的叶节点，这些节点通过最多 $\mathcal{O}(\mathrm{log}^2 N + R)$ 个内部节点连接。

因此，查询括号的最坏情况时间复杂度为 $\mathcal{O}(\mathrm{log}^2 N + R)$ 。

此外，这表明AST的最大高度为 $\mathcal{O}(\mathrm{log}^2 N)$ 。

增量更新

关于高效括号对着色的最有趣问题仍然悬而未决：给定当前的（平衡的）AST和一个替换某个范围的文本编辑，我们如何有效地更新树以反映文本编辑？

其思路是重用用于初始化的递归下降解析器，并添加缓存策略，以便可以重用和跳过不受文本编辑影响的节点。

当递归下降解析器在位置 $p$ 解析一组括号对，并且下一个编辑在位置 $e$ 时，它首先检查之前的抽象语法树（AST）是否在文本更改前的位置 $p$ 处有一个长度最多为 $e - p$ 的节点。如果是这种情况，这个节点不需要重新解析，底层的分词器只需按节点的长度前进。在消耗该节点后，解析继续。请注意，这个节点可以是一个单独的括号对或整个列表。此外，如果有多个这样的可重用节点，则应选择最长的节点。

以下示例显示了当插入单个开括号时（省略单个括号节点），哪些节点可以重用（以绿色显示）：

AST中的可重用节点

在通过重新解析包含编辑的节点并重用所有未更改的节点来处理文本编辑后，更新后的AST如下所示。请注意，所有11个可重用节点可以通过消耗3个节点B、H和G来重用，只有4个节点必须重新创建（以橙色显示）：

更新后的AST

正如这个例子所示，平衡列表不仅使查询变得快速，还有助于一次性重用大量节点。

算法复杂度

可以随意跳过关于算法复杂度的部分。

假设文本编辑替换了一个大小最多为 $E$ 的范围，并用最多 $E$ 个新字符替换。我们现在也暂时忽略那些没有对应开括号的闭括号的罕见情况。

我们只需要重新解析与编辑范围相交的节点。因此，最多需要重新解析 $\mathcal{O}(\mathrm{log}^2 N + E)$ 个节点（与查询括号的时间复杂度的推理相同）- 所有其他节点都可以重用。

显然，如果一个节点不与编辑范围相交，那么它的任何子节点也不会相交。因此，我们只需要考虑重用那些不与编辑范围相交但其父节点与编辑范围相交的节点（这将隐式重用所有节点及其父节点都不与编辑范围相交的节点）。此外，这些父节点不能被编辑范围完全覆盖，否则它们的所有子节点都将与编辑范围相交。然而，AST中的每一层最多只有两个节点部分与编辑范围相交。由于AST最多有 $\mathcal{O}(\mathrm{log}^2 N)$ 多层（受限于AST的高度），并且每个节点最多有3个子节点，所有可重用的节点最多可以通过消耗 $\mathcal{O}(2 \cdot 3 \cdot \mathrm{log}^2 N) = \mathcal{O}(\mathrm{log}^2 N)$ 节点来覆盖。

因此，为了构建更新后的树，我们需要重新解析最多 $\mathcal{O}(\mathrm{log}^2 N + E)$ 多个节点，并且可以重用 $\mathcal{O}(\mathrm{log}^2 N)$ 多个节点。

这也将决定更新操作的时间复杂度，但有一个注意事项。

我们如何重新平衡AST？

不幸的是，最后一个例子中的树不再平衡。

当将重用的列表节点与新解析的节点结合时，我们必须做一些工作来维护(2,3)-树属性。我们知道重用的和新解析的节点已经是(2,3)-树，但它们可能有不同的高度——因此我们不能仅仅创建父节点，因为(2,3)-树节点的所有子节点必须具有相同的高度。

我们如何高效地将这些高度混合的节点连接成一个单一的(2,3)-树？

这可以很容易地简化为将较小的树前置或附加到较大的树的问题：如果两棵树的高度相同，只需创建一个包含两个子节点的列表即可。否则，我们将高度为 $h_1$ 的较小树插入到高度为 $h_2$ 的较大树中，并且如果它们最终有超过3个子节点，则可能会拆分节点（类似于(2,3)-树的插入操作的工作方式）。

因为运行时间为 $\mathcal{O}(h_2 - h_1)$ ，我们取3个相邻的节点（ $a$ 、 $b$ 和 $c$ ），我们想要连接它们，并首先连接 $a$ 和 $b$ 或 $b$ 和 $c$ （可能会增加树的高度），具体取决于哪一对的高度差较小。这个过程会重复，直到所有节点都被连接。作为额外的优化，我们寻找具有相同高度的节点序列，并在线性时间内为它们创建父列表。

为了平衡前一个例子中的列表α和γ，我们对它们的子节点执行concat操作（红色列表违反了(2,3)-树属性，橙色节点具有意外的高度，绿色节点在重新平衡时被重新创建）：

平衡列表后的AST

因为列表B在不平衡树中的高度为2，而括号对β的高度为0，我们需要将β附加到B上，并完成列表α的处理。剩下的(2,3)-树是B，因此它成为新的根并替换列表α。继续处理γ，其子节点δ和H的高度为0，而G的高度为1。

我们首先将δ和H连接起来，并创建一个高度为1的新父节点Y（因为δ和H具有相同的高度）。然后我们将Y和G连接起来，并创建一个新的父列表X（出于同样的原因）。X随后成为父括号对的新子节点，替换了不平衡的列表γ。

在示例中，平衡操作有效地将最顶层列表的高度从3降低到2。然而，AST的总高度从4增加到5，这对最坏情况下的查询时间产生了负面影响。这是由于括号对β引起的，它在平衡列表树中充当叶子，但实际上包含另一个高度为2的列表。

在平衡父列表时考虑β的内部AST高度可能会改善最坏情况，但这将偏离(2,3)-树的理论。

算法复杂度

可以随意跳过关于算法复杂度的部分。

我们必须连接最多 $\mathcal{O}(\mathrm{log}^2 N)$ 多个节点，这些节点的最大列表高度为 $\mathcal{O}(\mathrm{log} N)$ （那些我们重用的节点），以及额外的 $\mathcal{O}(\mathrm{log}^2 N + E)$ 多个列表高度为0的节点（那些我们重新解析的节点）。

因为连接两个不同高度的节点具有时间复杂度 $\mathcal{O}(\mathrm{log} N)$ ，并且列表中所有重新解析的节点都是相邻的且具有列表高度 0，整个更新操作的时间复杂度最多为 $\mathcal{O}(\mathrm{log}^3 N + E)$ ，前提是找到一个可重用的节点可以足够快地完成。

我们如何高效地找到可重用的节点？

我们有两个数据结构用于此任务：编辑前位置映射器和节点读取器。

位置映射器将新文档中的位置（在应用编辑后）映射到旧文档（在应用编辑前），如果可能的话。它还告诉我们当前位置与下一个编辑之间的长度（如果我们在编辑中，则为0）。这是在 $\mathcal{O}(1)$ 中完成的。

在处理文本编辑和解析节点时，此组件为我们提供了可以潜在重用的节点的位置以及该节点可以具有的最大长度 - 显然，我们希望重用的节点必须比到下一个编辑的距离短。

节点读取器可以快速找到在AST中给定位置满足给定谓词的最长节点。为了找到一个我们可以重用的节点，我们使用位置映射器查找其旧位置及其最大允许长度，然后使用节点读取器找到该节点。如果我们找到了这样的节点，我们知道它没有改变，可以重用它并跳过其长度。

因为节点读取器是通过单调递增的位置进行查询的，所以它不必每次都从头开始搜索，而是可以从上次重用的节点的末尾开始搜索。关键在于一种无递归的树遍历算法，该算法可以深入节点，也可以跳过它们或返回到父节点。当找到一个可重用的节点时，遍历停止并继续处理节点读取器的下一个请求。

查询节点读取器一次的复杂度最高为 $\mathcal{O}(\mathrm{log}^2 N)$ ，但我们非常确定，单个更新操作发出的所有请求的平摊复杂度也是 $\mathcal{O}(\mathrm{log}^2 N)$ 。毕竟，节点读取器仅查询不受文本编辑影响的位置，并且始终从最后一个可重用节点到下一个可重用节点采取最短路径。因此，我们认为节点读取器的效率足够高，不会影响更新算法的运行时复杂度。

令牌更新

当在长的C风格文档的开头插入/*时，如果文档中不包含文本*/，整个文档将变成一个单一的注释，所有的标记都会改变。

由于令牌是在渲染器进程中同步计算的，如果不冻结用户界面，重新标记化无法立即进行。

相反，令牌会随着时间的推移分批更新，这样JavaScript事件循环就不会被阻塞太长时间。虽然这种方法不会减少总的阻塞时间，但它提高了更新期间UI的响应性。在最初对文档进行标记化时，也使用了相同的机制。

幸运的是，由于括号对AST的增量更新机制，我们可以立即应用这种批量的令牌更新，将更新视为一个单一的文本编辑，用自身替换重新令牌化的范围。一旦所有令牌更新完成，括号对AST保证会处于与从头创建相同的状态——即使在使用者编辑文档时重新令牌化仍在进行中。

这样，即使文档中的所有标记都发生变化，不仅标记化性能良好，而且括号对颜色化也是如此。

然而，当文档中包含大量注释中的不平衡括号时，文档末尾的括号颜色可能会闪烁，因为括号对解析器会学习到这些括号应该被忽略。

为了避免在打开文档并导航到其末尾时括号对颜色的闪烁，我们维护两个括号对的抽象语法树（AST），直到初始的标记化过程完成。第一个AST是在没有标记信息的情况下构建的，并且不会接收标记更新。第二个AST最初是第一个AST的克隆，但随着标记化的进行和标记更新的应用，它会接收标记更新并逐渐与第一个AST产生差异。最初，使用第一个AST来查询括号，但一旦文档完全标记化，第二个AST就会接管。

因为深度克隆几乎与重新解析文档一样昂贵，我们实现了写时复制，使得克隆可以在 $\mathcal{O}(1)$ 中完成。

长度的编码

编辑器视图描述了带有行号和列号的视口。颜色装饰也应表示为基于行/列的范围。

为了避免在基于偏移量和基于行/列的位置之间进行转换（这可以在 $\mathcal{O}(\mathrm{log} N)$ 中完成），我们也对AST使用基于行/列的长度。

请注意，这种方法与直接通过行索引的数据结构（例如使用字符串数组来描述文档的行内容）有显著不同。特别是，这种方法可以在行之间和行内进行单一二进制搜索。

将两个这样的长度相加很容易，但需要进行情况区分：虽然行数直接相加，但只有在第二个长度跨越零行时，才包括第一个长度的列数。

令人惊讶的是，大多数代码不需要知道长度是如何表示的。只有位置映射器变得更加复杂，因为必须注意一行可以包含多个文本编辑。

作为一个实现细节，我们将这些长度编码为一个单一的数字以减少内存压力。JavaScript 支持最大到 $2^{53} - 1$ 的整数，因此我们可以为行数和列数各使用最多 26 位。不幸的是，v8 将大于 $2^{31}$ 的数字存储在堆中，因此这种编码技巧并没有像我们想象的那样有效。

进一步的困难：未闭合的括号对

到目前为止，我们假设所有的括号对都是平衡的。然而，我们也希望支持未闭合和未打开的括号对。递归下降解析器的美妙之处在于，我们可以使用锚点集来改进错误恢复。

考虑以下示例：

( [1]
} [2]
) [3]

显然，在[2]处的}没有关闭任何括号对，并且代表一个未打开的括号。在[1]和[3]处的括号匹配得很好。然而，当在文档开头插入{时，情况发生了变化：

{ [0]
( [1]
} [2]
) [3]

现在，[0] 和 [2] 应该匹配，而 [1] 是一个未闭合的括号，[3] 是一个未打开的括号。

特别是，在以下示例中，[1] 应该是一个在 [2] 之前结束的未闭合括号：

{
    ( [1]
} [2]
{}

否则，打开一个括号可能会改变不相关的后续括号对的嵌套级别。

为了支持这种错误恢复，可以使用锚点集来跟踪调用者可以继续的预期标记集。在前一个示例中的位置[1]，锚点集将是 $\{$ } $\}$ 。因此，当解析[1]处的括号对时，发现[2]处的意外括号 }，它不会消耗它并返回一个未闭合的括号对。

在第一个例子中，设置在[2]的锚点是 $\{$ ) $\}$ ，但意外的字符是}。因为它不是锚点集的一部分，所以被报告为未打开的括号。

在重用节点时需要考虑这一点：当在( } )前加上{时，这对( } )不能被重用。我们使用位集来编码锚点集，并为每个节点计算未打开的括号集。如果它们相交，我们就不能重用该节点。幸运的是，只有少数几种括号类型，所以这对性能影响不大。

前进

高效的括号对着色是一个有趣的挑战。使用新的数据结构，我们还可以更有效地解决与括号对相关的其他问题，例如通用括号匹配或显示彩色行范围。

尽管JavaScript可能不是编写高性能代码的最佳语言，但通过减少渐近算法复杂度，尤其是在处理大量输入时，可以显著提高速度。

编程快乐！

Henning Dieterichs, VS Code 团队成员 @hediet_dev