The WITH clause allows you to specify common table expressions (CTEs). Regular (non-recursive) common-table-expressions are essentially views that are limited in scope to a particular query. CTEs can reference each-other and can be nested.
Basic CTE Examples
Create a CTE called "cte" and use it in the main query:
WITH cte AS (SELECT 42 AS x)
SELECT * FROM cte;
| x |
|---|
| 42 |
Create two CTEs, where the second CTE references the first CTE:
WITH cte AS (SELECT 42 AS i),
cte2 AS (SELECT i * 100 AS x FROM cte)
SELECT * FROM cte2;
| x |
|---|
| 4200 |
Materialized CTEs
By default, CTEs are inlined into the main query. Inlining can result in duplicate work, because the definition is copied for each reference. Take this query for example:
WITH t(x) AS (⟨Q_t⟩)
SELECT * FROM t AS t1,
t AS t2,
t AS t3;
Inlining duplicates the definition of t for each reference which results in the following query:
SELECT * FROM (⟨Q_t⟩) AS t1(x),
(⟨Q_t⟩) AS t2(x),
(⟨Q_t⟩) AS t3(x);
If ⟨Q_t⟩ is expensive, materializing it with the MATERIALIZED keyword can improve performance. In this case, ⟨Q_t⟩ is evaluated only once.
WITH t(x) AS MATERIALIZED (⟨Q_t⟩)
SELECT * FROM t AS t1,
t AS t2,
t AS t3;
Recursive CTEs
WITH RECURSIVE allows the definition of CTEs which can refer to themselves. Note that the query must be formulated in a way that ensures termination, otherwise, it may run into an infinite loop.
Example: Fibonacci Sequence
WITH RECURSIVE can be used to make recursive calculations. For example, here is how WITH RECURSIVE could be used to calculate the first ten Fibonacci numbers:
WITH RECURSIVE FibonacciNumbers (RecursionDepth, FibonacciNumber, NextNumber) AS (
-- Base case
SELECT
0 AS RecursionDepth,
0 AS FibonacciNumber,
1 AS NextNumber
UNION ALL
-- Recursive step
SELECT
fib.RecursionDepth + 1 AS RecursionDepth,
fib.NextNumber AS FibonacciNumber,
fib.FibonacciNumber + fib.NextNumber AS NextNumber
FROM
FibonacciNumbers fib
WHERE
fib.RecursionDepth + 1 < 10
)
Query the CTE:
SELECT
fn.RecursionDepth AS FibonacciNumberIndex,
fn.FibonacciNumber
FROM
FibonacciNumbers fn;
| FibonacciNumberIndex | FibonacciNumber |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
Example: Tree Traversal
WITH RECURSIVE can be used to traverse trees. For example, take a hierarchy of tags:
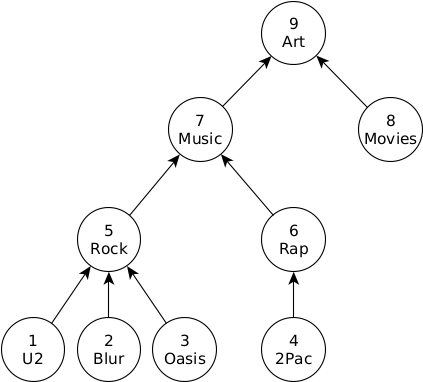
CREATE TABLE tag (id INTEGER, name VARCHAR, subclassof INTEGER);
INSERT INTO tag VALUES
(1, 'U2', 5),
(2, 'Blur', 5),
(3, 'Oasis', 5),
(4, '2Pac', 6),
(5, 'Rock', 7),
(6, 'Rap', 7),
(7, 'Music', 9),
(8, 'Movies', 9),
(9, 'Art', NULL);
The following query returns the path from the node Oasis to the root of the tree (Art).
WITH RECURSIVE tag_hierarchy(id, source, path) AS (
SELECT id, name, [name] AS path
FROM tag
WHERE subclassof IS NULL
UNION ALL
SELECT tag.id, tag.name, list_prepend(tag.name, tag_hierarchy.path)
FROM tag, tag_hierarchy
WHERE tag.subclassof = tag_hierarchy.id
)
SELECT path
FROM tag_hierarchy
WHERE source = 'Oasis';
| path |
|---|
| [Oasis, Rock, Music, Art] |
Graph Traversal
The WITH RECURSIVE clause can be used to express graph traversal on arbitrary graphs. However, if the graph has cycles, the query must perform cycle detection to prevent infinite loops.
One way to achieve this is to store the path of a traversal in a list and, before extending the path with a new edge, check whether its endpoint has been visited before (see the example later).
Take the following directed graph from the LDBC Graphalytics benchmark:
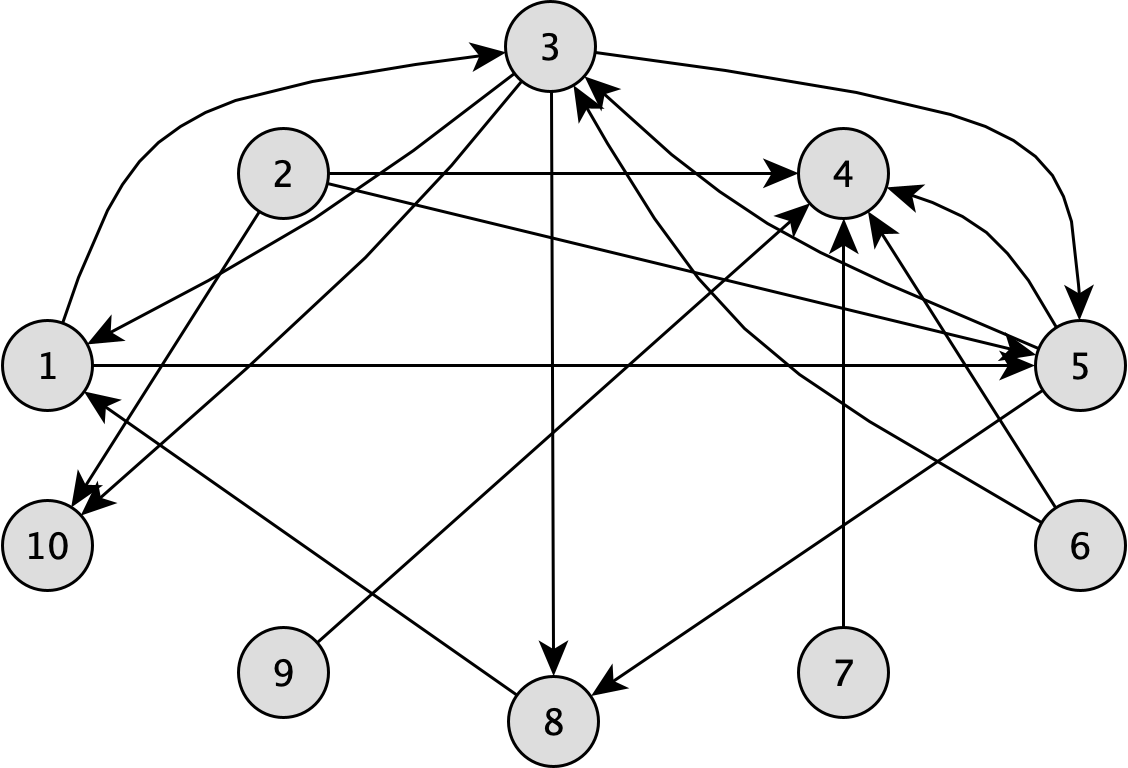
CREATE TABLE edge (node1id INTEGER, node2id INTEGER);
INSERT INTO edge
VALUES
(1, 3), (1, 5), (2, 4), (2, 5), (2, 10), (3, 1), (3, 5), (3, 8), (3, 10),
(5, 3), (5, 4), (5, 8), (6, 3), (6, 4), (7, 4), (8, 1), (9, 4);
Note that the graph contains directed cycles, e.g., between nodes 1, 2, and 5.
Enumerate All Paths from a Node
The following query returns all paths starting in node 1:
WITH RECURSIVE paths(startNode, endNode, path) AS (
SELECT -- define the path as the first edge of the traversal
node1id AS startNode,
node2id AS endNode,
[node1id, node2id] AS path
FROM edge
WHERE startNode = 1
UNION ALL
SELECT -- concatenate new edge to the path
paths.startNode AS startNode,
node2id AS endNode,
array_append(path, node2id) AS path
FROM paths
JOIN edge ON paths.endNode = node1id
-- Prevent adding a repeated node to the path.
-- This ensures that no cycles occur.
WHERE node2id != ALL(paths.path)
)
SELECT startNode, endNode, path
FROM paths
ORDER BY length(path), path;
| startNode | endNode | path |
|---|---|---|
| 1 | 3 | [1, 3] |
| 1 | 5 | [1, 5] |
| 1 | 5 | [1, 3, 5] |
| 1 | 8 | [1, 3, 8] |
| 1 | 10 | [1, 3, 10] |
| 1 | 3 | [1, 5, 3] |
| 1 | 4 | [1, 5, 4] |
| 1 | 8 | [1, 5, 8] |
| 1 | 4 | [1, 3, 5, 4] |
| 1 | 8 | [1, 3, 5, 8] |
| 1 | 8 | [1, 5, 3, 8] |
| 1 | 10 | [1, 5, 3, 10] |
Note that the result of this query is not restricted to shortest paths, e.g., for node 5, the results include paths [1, 5] and [1, 3, 5].
Enumerate Unweighted Shortest Paths from a Node
In most cases, enumerating all paths is not practical or feasible. Instead, only the (unweighted) shortest paths are of interest. To find these, the second half of the WITH RECURSIVE query should be adjusted such that it only includes a node if it has not yet been visited. This is implemented by using a subquery that checks if any of the previous paths includes the node:
WITH RECURSIVE paths(startNode, endNode, path) AS (
SELECT -- define the path as the first edge of the traversal
node1id AS startNode,
node2id AS endNode,
[node1id, node2id] AS path
FROM edge
WHERE startNode = 1
UNION ALL
SELECT -- concatenate new edge to the path
paths.startNode AS startNode,
node2id AS endNode,
array_append(path, node2id) AS path
FROM paths
JOIN edge ON paths.endNode = node1id
-- Prevent adding a node that was visited previously by any path.
-- This ensures that (1) no cycles occur and (2) only nodes that
-- were not visited by previous (shorter) paths are added to a path.
WHERE NOT EXISTS (SELECT 1
FROM paths previous_paths
WHERE list_contains(previous_paths.path, node2id))
)
SELECT startNode, endNode, path
FROM paths
ORDER BY length(path), path;
| startNode | endNode | path |
|---|---|---|
| 1 | 3 | [1, 3] |
| 1 | 5 | [1, 5] |
| 1 | 8 | [1, 3, 8] |
| 1 | 10 | [1, 3, 10] |
| 1 | 4 | [1, 5, 4] |
| 1 | 8 | [1, 5, 8] |
Enumerate Unweighted Shortest Paths between Two Nodes
WITH RECURSIVE can also be used to find all (unweighted) shortest paths between two nodes. To ensure that the recursive query is stopped as soon as we reach the end node, we use a window function which checks whether the end node is among the newly added nodes.
The following query returns all unweighted shortest paths between nodes 1 (start node) and 8 (end node):
WITH RECURSIVE paths(startNode, endNode, path, endReached) AS (
SELECT -- define the path as the first edge of the traversal
node1id AS startNode,
node2id AS endNode,
[node1id, node2id] AS path,
(node2id = 8) AS endReached
FROM edge
WHERE startNode = 1
UNION ALL
SELECT -- concatenate new edge to the path
paths.startNode AS startNode,
node2id AS endNode,
array_append(path, node2id) AS path,
max(CASE WHEN node2id = 8 THEN 1 ELSE 0 END)
OVER (ROWS BETWEEN UNBOUNDED PRECEDING
AND UNBOUNDED FOLLOWING) AS endReached
FROM paths
JOIN edge ON paths.endNode = node1id
WHERE NOT EXISTS (SELECT 1
FROM paths previous_paths
WHERE list_contains(previous_paths.path, node2id))
AND paths.endReached = 0
)
SELECT startNode, endNode, path
FROM paths
WHERE endNode = 8
ORDER BY length(path), path;
| startNode | endNode | path |
|---|---|---|
| 1 | 8 | [1, 3, 8] |
| 1 | 8 | [1, 5, 8] |
