scipy.signal.

连贯性#

scipy.signal.coherence(x, y, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', axis=-1)[源代码][源代码]#

使用 Welch 方法估计离散时间信号 X 和 Y 的幅值平方相干估计 Cxy。

Cxy = abs(Pxy)**2/(Pxx*Pyy)，其中 Pxx 和 Pyy 是 X 和 Y 的功率谱密度估计，Pxy 是 X 和 Y 的互谱密度估计。

参数:

xarray_like: 测量值的时间序列
yarray_like: 测量值的时间序列
fsfloat, 可选: x 和 y 时间序列的采样频率。默认为 1.0。
窗口str 或 tuple 或 array_like，可选: 要使用的期望窗口。如果 window 是一个字符串或元组，它会被传递给 get_window 以生成窗口值，这些值默认是 DFT-even 的。请参阅 get_window 以获取窗口列表和所需参数。如果 window 是类数组，它将直接用作窗口，其长度必须为 nperseg。默认为汉宁窗口。
npersegint, 可选: 每个片段的长度。默认为 None，但如果 window 是 str 或 tuple，则设置为 256，如果 window 是 array_like，则设置为 window 的长度。
noverlap: int, 可选: 段落之间重叠的点数。如果为 None，则 noverlap = nperseg // 2。默认为 None。
nfftint, 可选: 使用的FFT长度，如果需要零填充FFT。如果为 None，则FFT长度为 nperseg。默认为 None。
detrend : str 或 function 或 False, 可选字符串或函数或: 指定如何去趋势化每个片段。如果 detrend 是一个字符串，它将作为 type 参数传递给 detrend 函数。如果它是一个函数，它接受一个片段并返回一个去趋势化的片段。如果 detrend 是 False，则不进行去趋势化。默认为 ‘constant’。
轴int, 可选: 计算两个输入的相关性时沿用的轴；默认是沿最后一个轴（即 axis=-1）。

返回:

fndarray: 样本频率数组。
Cxyndarray: x 和 y 的幅度平方相干性。

参见

periodogram: 简单的，可选择修改的周期图
lombscargle: 不均匀采样数据的Lomb-Scargle周期图
welch: 通过 Welch 方法的功率谱密度。
csd: 通过 Welch 方法计算的交叉谱密度。

注释

适当的重叠量将取决于窗口的选择和您的需求。对于默认的Hann窗口，50%的重叠是一个合理的折中，既能准确估计信号功率，又不会过度计算任何数据。较窄的窗口可能需要更大的重叠。

Added in version 0.16.0.

参考文献

[1]

P. Welch, “The use of the fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms”, IEEE Trans. Audio Electroacoust. vol. 15, pp. 70-73, 1967.

[2]

Stoica, Petre, 和 Randolph Moses, “信号的频谱分析” Prentice Hall, 2005

示例

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

生成两个具有一些共同特征的测试信号。

>>> fs = 10e3
>>> N = 1e5
>>> amp = 20
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> b, a = signal.butter(2, 0.25, 'low')
>>> x = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
>>> y = signal.lfilter(b, a, x)
>>> x += amp*np.sin(2*np.pi*freq*time)
>>> y += rng.normal(scale=0.1*np.sqrt(noise_power), size=time.shape)

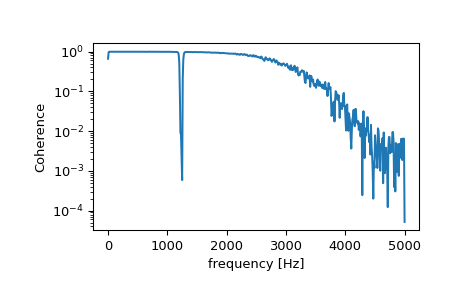
计算并绘制相干性。

>>> f, Cxy = signal.coherence(x, y, fs, nperseg=1024)
>>> plt.semilogy(f, Cxy)
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Coherence')
>>> plt.show()

../../_images/scipy-signal-coherence-1.png