快速傅里叶变换预测模型 (FFT)¶
以下是对FFT预测模型的简要演示。该模型特别适用于季节性非常强的数据。本演示选择的样本数据也相应地进行了选择。
[1]:
# fix python path if working locally
from utils import fix_pythonpath_if_working_locally
fix_pythonpath_if_working_locally()
[2]:
%load_ext autoreload
%autoreload 2
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from darts import TimeSeries
from darts.models import FFT, AutoARIMA, ExponentialSmoothing, Theta
from darts.metrics import mae
from darts.utils.missing_values import fill_missing_values
from darts.datasets import TemperatureDataset, AirPassengersDataset, EnergyDataset
import warnings
warnings.filterwarnings("ignore")
import logging
logging.disable(logging.CRITICAL)
Importing plotly failed. Interactive plots will not work.
读取和格式化¶
这里我们简单地读取包含每日温度的CSV文件,并将这些值转换为所需格式。
[3]:
ts = TemperatureDataset().load()
构建用于训练和验证的 TimeSeries 实例¶
[4]:
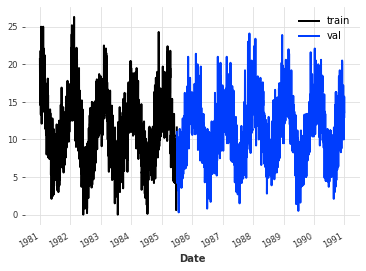
train, val = ts.split_after(pd.Timestamp("19850701"))
train.plot(label="train")
val.plot(label="val")
基本FFT模型¶
[5]:
model = FFT(required_matches=set(), nr_freqs_to_keep=None)
model.fit(train)
pred_val = model.predict(len(val))
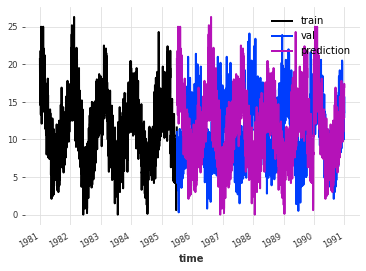
下图向我们展示了,使用随机分割的训练-测试集进行简单的DFT很可能会导致糟糕的结果。仔细观察后我们可以看到,预测结果(紫色)仅仅是重复了训练集(蓝色)。这是DFT的标准行为,而且它本身相当无用,因为重复训练集可以更高效地完成。针对这种方法进行了三项改进。
[6]:
train.plot(label="train")
val.plot(label="val")
pred_val.plot(label="prediction")
print("MAE:", mae(pred_val, val))
MAE: 5.424526892430279
改进1:裁剪训练集¶
第一个改进是在将训练集输入FFT算法之前对其进行裁剪,使得裁剪后的序列中的第一个时间戳与要预测的第一个时间戳在季节性方面匹配,即它们具有相同的月份、日期、星期几、一天中的时间等。我们可以通过向FFT构造函数传递可选参数``required_matches``来实现这一点,该参数明确告诉我们的模型哪些时间戳属性是相关的。但实际上,如果我们不手动设置它,模型将尝试自动找到相关的pd.Timestamp属性,并相应地裁剪训练集(我们将在这里这样做)。
[7]:
model = FFT(nr_freqs_to_keep=None)
model.fit(train)
pred_val = model.predict(len(val))
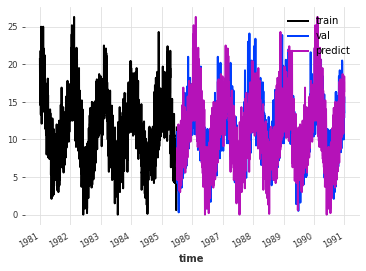
我们可以看到,预测结果的季节性与验证集的季节性很好地对齐了。然而,我们仍然只是在重复训练集,包括所有的噪声。从误差来看,这仍然是一个相当糟糕的预测。
[8]:
train.plot(label="train")
val.plot(label="val")
pred_val.plot(label="predict")
print("MAE:", mae(pred_val, val))
MAE: 3.0995766932270916
改进2:过滤掉低振幅波¶
DFT 分解到频域允许我们选择性地过滤掉低振幅的波。这使我们能够在保留强季节性趋势的同时丢弃一些噪声。在 FFT 模型中,这是通过传递可选参数 nr_freqs_to_keep 来实现的。该参数表示将保留的总频率数。例如,如果传递值为 20,则仅使用振幅最高的 20 个频率。默认值设置为 10。
[9]:
model = FFT(nr_freqs_to_keep=20)
model.fit(train)
pred_val = model.predict(len(val))
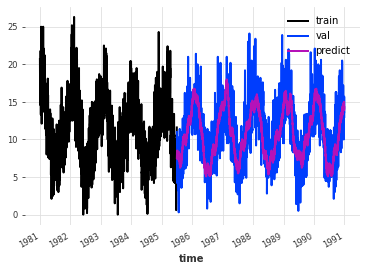
我们得到了一个噪声较小的信号。根据数据集的不同,这可能是一个更好的预测。查看误差指标,我们可以看到这个模型比之前的模型表现要好得多。
[10]:
train.plot(label="train")
val.plot(label="val")
pred_val.plot(label="predict")
print("MAE:", mae(pred_val, val))
MAE: 2.2941917142812893
改进3:去趋势化¶
让我们尝试一个具有全球上升趋势的不同数据集
[11]:
ts_2 = AirPassengersDataset().load()
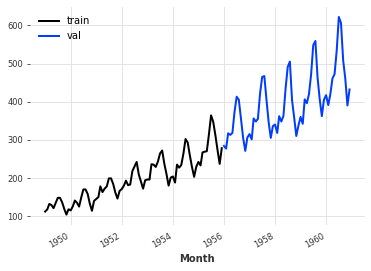
train, val = ts_2.split_after(pd.Timestamp("19551201"))
train.plot(label="train")
val.plot(label="val")
[12]:
model = FFT()
model.fit(train)
pred_val = model.predict(len(val))
显然,我们的模型在包含上升趋势方面完全失败了。由于这种趋势,我们的模型也无法识别月度季节性。
[13]:
train.plot(label="train")
val.plot(label="val")
pred_val.plot(label="prediction")
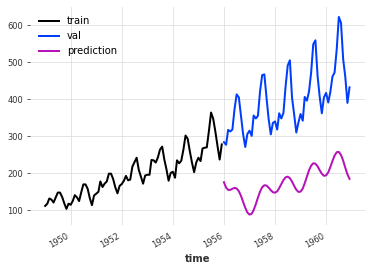
这个问题可以通过将可选的 trend 参数设置为 ‘poly’ 或 ‘exp’ 来解决,这会拟合一个多项式或指数函数到数据中,并在进行 DFT 之前减去它。在预测时,趋势会被再次加上。
[14]:
model = FFT(trend="poly")
model.fit(train)
pred_val = model.predict(len(val))
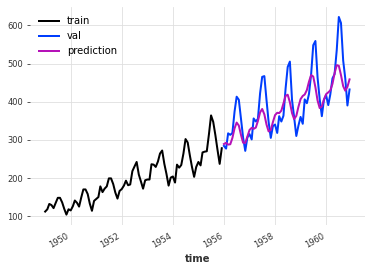
我们现在有了更好的预测。
[15]:
train.plot(label="train")
val.plot(label="val")
pred_val.plot(label="prediction")
新数据:每小时核能发电量¶
[16]:
ts_3 = EnergyDataset().load()
ts_3 = fill_missing_values(ts_3, "auto")
ts_3 = ts_3["generation nuclear"]
train, val = ts_3.split_after(pd.Timestamp("2017-07-01"))
train.plot(label="train")
val.plot(label="val")
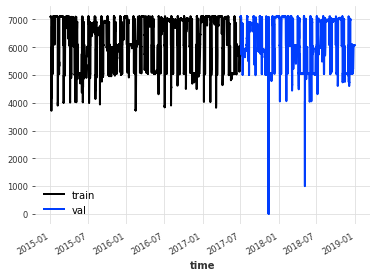
我们不仅可以简单地查看 FFT 模型的性能,还可以查看其他一系列预测模型在这个新数据集上的 MAE 表现。令人惊讶的是,在这个数据集上,FFT 模型优于所有其他模型(至少在默认参数下)。当然,这个数据集因其高度季节性而被特别选中。然而,这表明 FFT 有其应用场景。此外,FFT 模型的运行时间比其他模型短得多!
[17]:
models = [AutoARIMA(), ExponentialSmoothing(), Theta(), FFT()]
for model in models:
model.fit(train)
pred_val = model.predict(len(val))
print(str(model) + " MAE: " + str(mae(pred_val, val)))
Auto-ARIMA MAE: 956.1953089418552
Prophet MAE: 653.8682864837639
Exponential smoothing MAE: 1667.805755244887
Theta(2) MAE: 944.0038491197353
FFT(nr_freqs_to_keep=10, trend=None) MAE: 643.337489093281