回归模型

以下是对 Darts 中回归模型的深入演示 - 从基本到高级功能，包括：

• Darts 的回归模型

• 滞后和滞后数据提取

• 协变量使用

• 参数 output_chunk_length 与 multi_models 的关系

• 一次性预测和自回归预测

• 多输出支持

• 概率预测

• 可解释性

• 以及更多

# fix python path if working locally
from utils import fix_pythonpath_if_working_locally

fix_pythonpath_if_working_locally()

# activate javascript
from shap import initjs

initjs()

Using `tqdm.autonotebook.tqdm` in notebook mode. Use `tqdm.tqdm` instead to force console mode (e.g. in jupyter console)

%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.linear_model import BayesianRidge

from darts.models import (
    LinearRegressionModel,
    RegressionModel,
    LightGBMModel,
    XGBModel,
    CatBoostModel,
)
from darts.metrics import mape
from darts.datasets import ElectricityConsumptionZurichDataset
from darts.explainability import ShapExplainer

输入数据集

对于这个笔记本，我们使用了来自瑞士苏黎世家庭用电量的数据集。

该数据集的频率为每刻钟一次（15分钟时间间隔），但我们将其重新采样为每小时一次以保持简单。

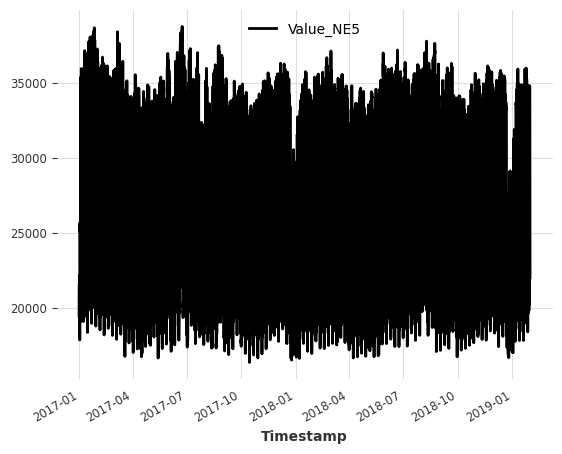
目标系列 (我们想要预测的系列): - Value_NE5: 电网级别5的家庭电力消耗 (以千瓦时为单位)。

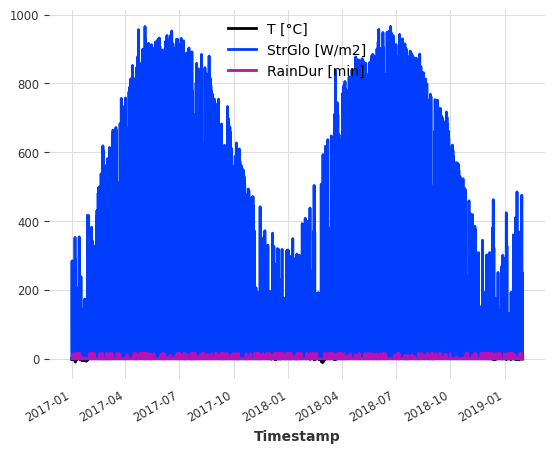
协变量**（用于帮助改进预测的外部数据）：数据集还包含我们可以用作协变量的天气测量数据。为简单起见，我们使用： - **T [°C]：测量的温度 - StrGlo [W/m2]：测量的太阳辐射 - RainDur [min]：测量的降雨持续时间

ts_energy = ElectricityConsumptionZurichDataset().load()

# extract values recorded between 2017 and 2019
start_date = pd.Timestamp("2017-01-01")
end_date = pd.Timestamp("2019-01-31")
ts_energy = ts_energy[start_date:end_date]

# resample to hourly frequency
ts_energy = ts_energy.resample(freq="H")

# extract temperature, solar irradiation and rain duration
ts_weather = ts_energy[["T [°C]", "StrGlo [W/m2]", "RainDur [min]"]]

# extract households energy consumption
ts_energy = ts_energy["Value_NE5"]

# create train and validation splits
validation_cutoff = pd.Timestamp("2018-10-31")
ts_energy_train, ts_energy_val = ts_energy.split_after(validation_cutoff)

ts_energy.plot()
plt.show()

ts_weather.plot()
plt.show()

Darts 回归模型

回归是一种统计方法，用于数据科学和机器学习中，以建模因变量（目标 y）与一个或多个自变量（特征 X）之间的关系。

为了方便，Darts 核心包自带了一些回归模型： - LinearRegressionModel 和 RandomForest：完全集成的 sklearn 模型 - RegressionModel：将 Darts 模型 API 包装在任何类似 sklearn 的模型周围 - XGBModel：围绕 XGBoost 的 XGBRegressor 的包装器

除了这些，我们还为一些最先进的回归模型提供了一个统一的API，可以按照我们的 安装指南 进行安装：

• LightGBMModel: 围绕 LightGBM 的 LightGBMRegressor 的包装器

• CatBoostModel: 围绕 CatBoost 的 CatBoostRegressor 的包装器。

在 Darts 中，预测问题通过将时间序列转换为两个表格数组，转化为回归问题：- X：特征或输入数组，形状为（样本数/观测数，特征数）- 特征数由（特定特征的）目标、过去和未来协变量的滞后总数给出。- y：目标或标签数组，形状为（样本数/观测数，目标数）- 目标数由模型参数 output_chunk_length 和 multi_models 给出（我们稍后会解释这一点）。

目标和协变量滞后

滞后特征是指相对于某个参考点，特征在之前或未来时间步的值。

在Darts中，滞后值指定了特征值相对于每个观察/样本（X``中的一行）的第一个预测目标时间步 ``y_t0 的位置。

• lag == 0: 第一个预测时间步 t0 的位置，例如 y_t0 的位置

• lag < 0: 所有位置在第一个预测时间步 t-1, t-2, … 的过去。

• lag > 0: 所有在第一个预测时间步 t+1, t+2, … 之后的未来位置

滞后选择在实现良好的预测准确性方面至关重要。我们希望模型能够接收到相关信息，以捕捉目标序列的时间特性/依赖关系（模式、季节性、趋势等）。它还对模型的性能/复杂性有重大影响，因为每个额外的滞后都会为 X 添加一个新特征。

在模型创建时，我们可以分别为目标序列和协变量序列设置滞后。

• lags: 目标序列（我们想要预测的那个）的滞后项

• lags_past_covariates: 可选地，过去协变量序列的滞后（外部过去观测特征，有助于提高预测）

• lags_future_covariates: 可选地，未来协变量序列的滞后（外部未来已知特征，有助于提高预测）

定义滞后的方式有多种 (int, List[int], Tuple[int, int], ...)。你可以在 RegressionModel 文档 中找到更多关于这方面的信息。

滞后数据提取

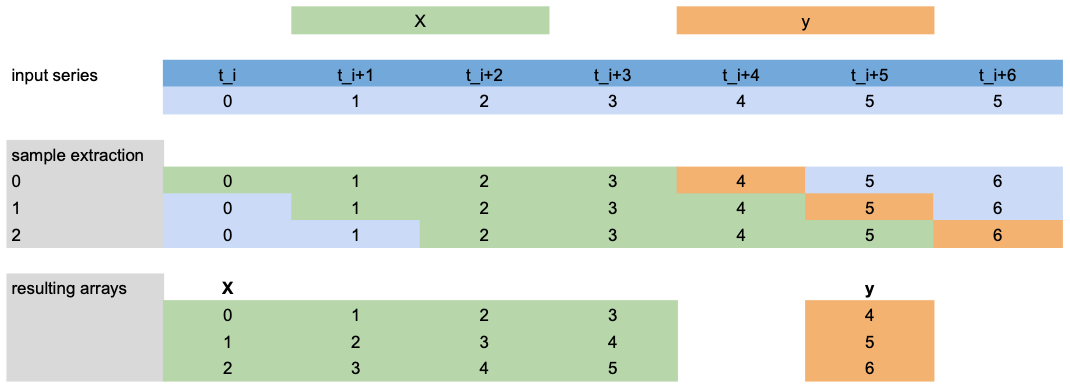
现在，让我们看看如何从下面的场景中提取 X 和 y 用于训练：

• lags=[-4,-3,-2,-1]: 使用第一个预测时间步（橙色）之前的最后4个目标值（绿色）作为 X 特征。

• output_chunk_length=1: 预测下一个 (1) 时间步的目标值 y (橙色)。

• 我们有一个包含7个时间步的目标序列 t_i, ..., t_i+6 (蓝色)。

注意：此示例仅展示目标 ``lags`` 提取，但同样适用于 ``lags_past/future_covariates``。

示例

让我们尝试将此应用于我们的电力数据集。假设我们想要预测训练集结束后的接下来几个小时的消耗量。

作为输入特征，我们提供它从一天前和两天前的同一小时的消费数据 -> lags=[-24, -48]。

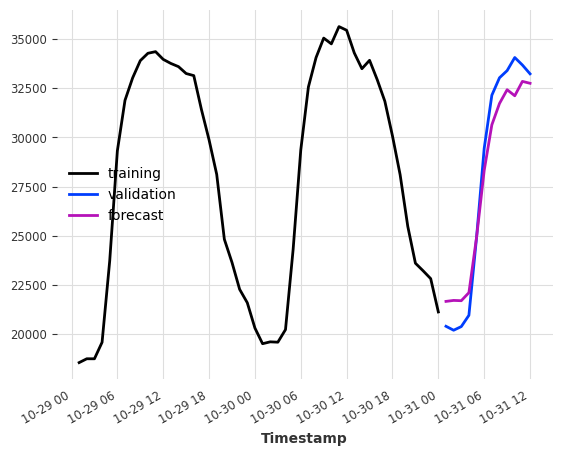
model = LinearRegressionModel(lags=[-24, -48])
model.fit(ts_energy_train)
pred = model.predict(12)

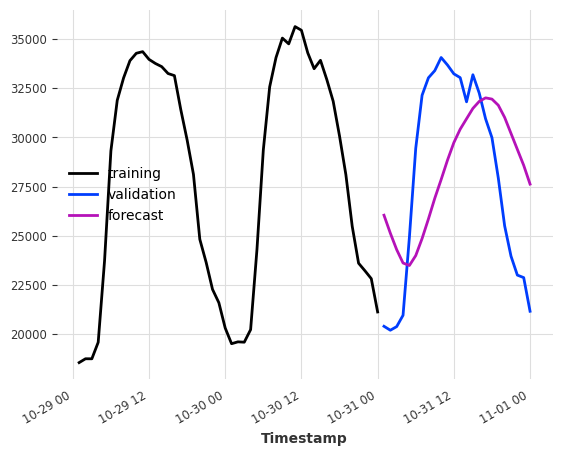
ts_energy_train[-48:].plot(label="training")
ts_energy_val[:12].plot(label="validation")
pred.plot(label="forecast")

<Axes: xlabel='Timestamp'>

基于协变量的预测

要在目标系列的历史数据旁边使用外部数据，我们指定过去和/或未来的协变量滞后，然后将 past_covariates 和/或 future_covariates 传递给 fit() 和 predict()。

让我们假设我们有的不是天气测量数据，而是天气预报。那么我们可以将它们用作 future_covariates。我们在这里仅出于演示目的这样做！

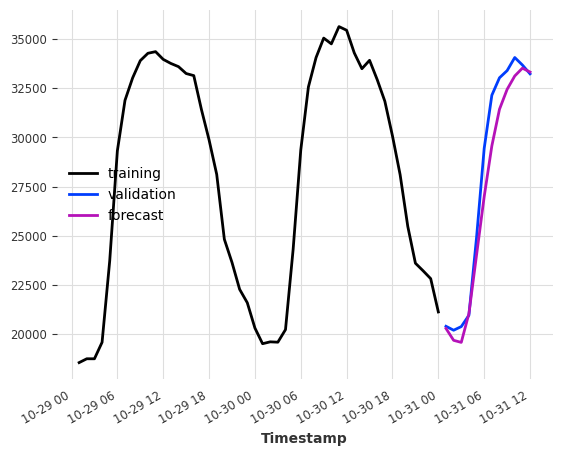
下面是一个使用过去24小时（24）的每小时目标序列（电力消耗）和我们的天气“预测”中预测时间步长（[0]）的值的示例。

model = LinearRegressionModel(lags=24, lags_future_covariates=[0])
model.fit(ts_energy_train, future_covariates=ts_weather)
pred = model.predict(12)

ts_energy_train[-48:].plot(label="training")
ts_energy_val[:12].plot(label="validation")
pred.plot(label="forecast")

<Axes: xlabel='Timestamp'>

仅使用协变量

有时，我们可能也对纯粹依赖协变量值的预测模型感兴趣。

为此，至少指定 lags_past_covariates 或 lags_future_covariates 中的一个，并将 lags 设置为 None。Darts 回归模型以监督方式进行训练，因此我们仍然需要提供训练的目标序列。

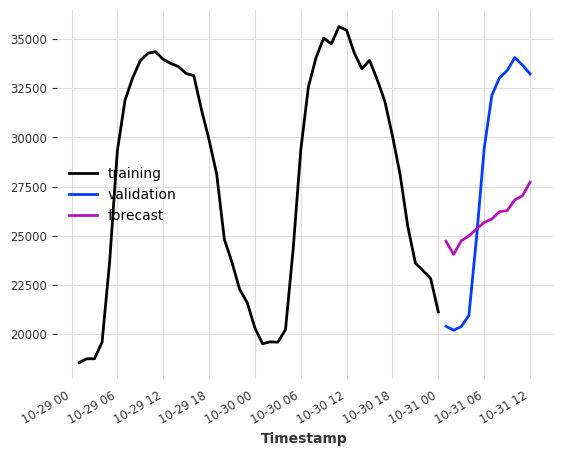
仅使用天气“预报”作为输入，我们能多好地预测电力消耗？

元组 (24, 1) 表示 (过去滞后的数量, 未来滞后的数量)。

model = LinearRegressionModel(lags=None, lags_future_covariates=(24, 1))
model.fit(series=ts_energy_train, future_covariates=ts_weather)
pred = model.predict(12)

ts_energy_train[-48:].plot(label="training")
ts_energy_val[:12].plot(label="validation")
pred.plot(label="forecast")

<Axes: xlabel='Timestamp'>

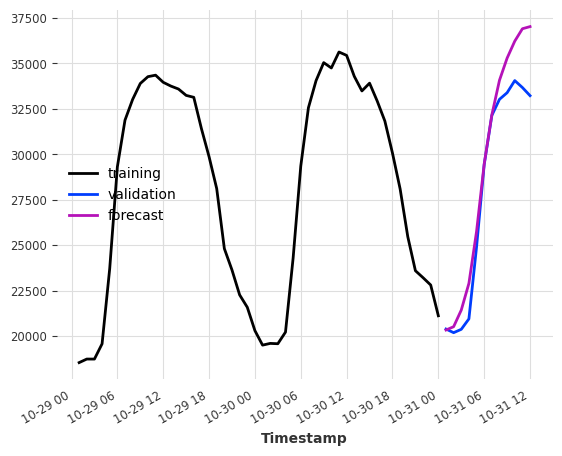
如果我们添加一些日历信息呢？我们可以使用 add_encoders 让模型免费生成日历属性编码。

model = LinearRegressionModel(
    lags=None,
    lags_future_covariates=(24, 1),
    add_encoders={
        "cyclic": {"future": ["minute", "hour", "dayofweek", "month"]},
        "tz": "CET",
    },
)
model.fit(series=ts_energy_train, future_covariates=ts_weather)
pred = model.predict(12)

ts_energy_train[-48:].plot(label="training")
ts_energy_val[:12].plot(label="validation")
pred.plot(label="forecast")
plt.show()

特定组件的延迟

如果目标或任何协变量是多元的（具有多个分量/列），我们可以为每个分量使用专门的滞后。只需将字典传递给 lags* 参数，其中分量名称作为键，滞后作为值。

在下面的示例中，我们将默认滞后设置为 (24,1)``（用于协变量组件 ``'T [°C]' 和 'StrGlo [W/ms]'），并为特征 'RainDur [min]' 指定一个专用滞后 [0]。

model = LinearRegressionModel(
    lags=None, lags_future_covariates={"default_lags": (24, 1), "RainDur [min]": [0]}
)
model.fit(series=ts_energy_train, future_covariates=ts_weather)
pred = model.predict(12)

ts_energy_train[-48:].plot(label="training data")
ts_energy_val[:12].plot(label="validation data")
pred.plot(label="forecast")

<Axes: xlabel='Timestamp'>

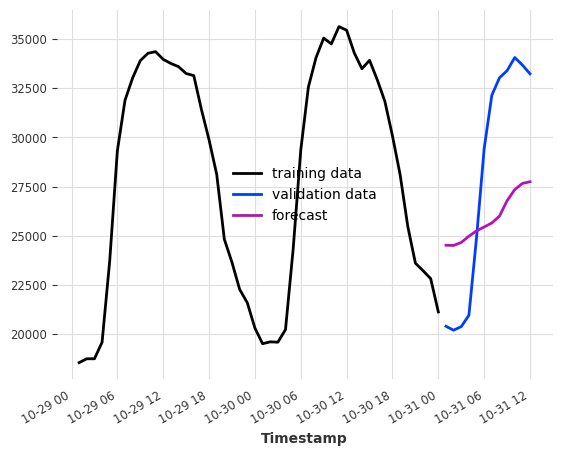
模型的输出块长度

此关键参数设置了 内部回归模型可以一次预测的时间步数 。

这与 predict() 中的预测范围 n 不同，后者是 期望 生成的预测点数量，可以通过以下方式实现：- 单次预测（如果 n <= output_chunk_length），或 - 自回归预测，消耗其自身的预测（以及协变量的未来值）作为额外预测的输入（否则）

例如，如果我们希望模型根据前一天的消费情况预测接下来24小时的电力消耗，设置 output_chunk_length=24 可以确保模型不会使用其预测值或未来协变量的值来预测整个一天。

model_auto_regression = LinearRegressionModel(lags=24, output_chunk_length=1)
model_single_shot = LinearRegressionModel(lags=24, output_chunk_length=24)

model_auto_regression.fit(ts_energy_train)
model_single_shot.fit(ts_energy_train)

pred_auto_regression = model_auto_regression.predict(24)
pred_single_shot = model_single_shot.predict(24)

ts_energy_train[-48:].plot(label="training data")
ts_energy_val[:24].plot(label="validation data")
pred_auto_regression.plot(label="forecast (auto-regression)")
pred_single_shot.plot(label="forecast (single-shot)")

<Axes: xlabel='Timestamp'>

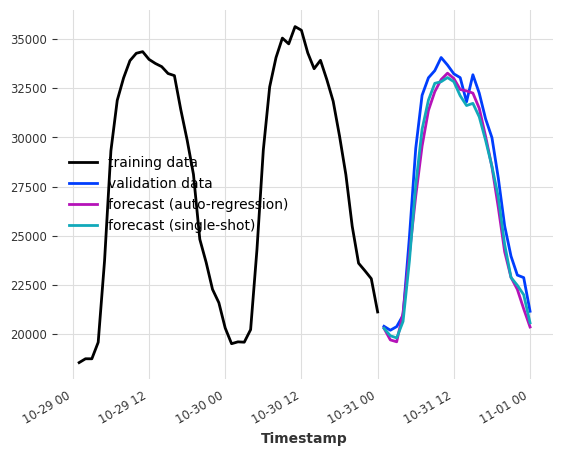
多模型预测

当 output_chunk_length>1 时，可以通过修改 multi_models 参数来进一步参数化模型行为。

multi_models=True 是 Darts 中的默认行为，如上所示。我们创建了 output_chunk_length 个模型的副本，并训练每个模型来预测 output_chunk_length 个时间步长中的一个（使用相同的输入）。这种方法在计算和内存上更为密集，但往往能产生更好的结果。

单模型预测

当 multi_model=False 时，我们使用单一模型，并训练它仅预测 output_chunk_length 中的最后一个点。这降低了模型复杂性，因为只会训练和存储一组系数。

我们仍然能够通过在表格化过程中移动滞后来预测从1到``output_chunk_length``的所有点。这意味着每个预测值都使用了一组新的输入值。由于移动，训练序列的最小长度要求也将增加。

multi_models = LinearRegressionModel(lags=24, output_chunk_length=24, multi_models=True)
single_model = LinearRegressionModel(
    lags=24, output_chunk_length=24, multi_models=False
)

multi_models.fit(ts_energy_train)
single_model.fit(ts_energy_train)

pred_multi_models = multi_models.predict(24)
pred_single_model = single_model.predict(24)

ts_energy_train[-48:].plot(label="training")
ts_energy_val[:24].plot(label="validation")
pred_multi_models.plot(label="forecast (multi models)")
pred_single_model.plot(label="forecast (single model)")

<Axes: xlabel='Timestamp'>

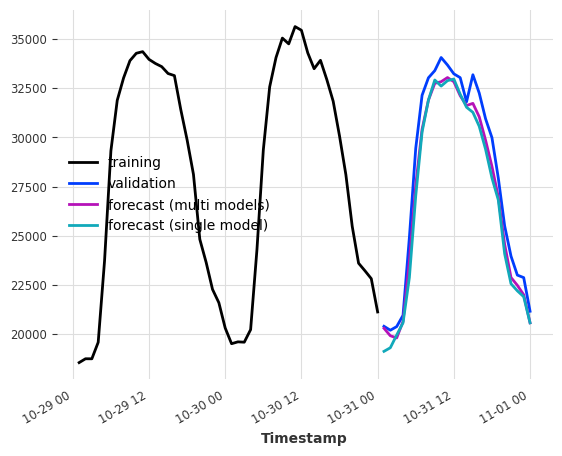
可视化

为了可视化内部发生的事情，让我们简化模型并展示不同参数的过程。

模型设置：LinearRegressionModel(lags=[-4, -3, -2, -1], output_chunk_length=2, multi_models=True)。

当调用 predict(n=4) 时，输入序列的处理如下：

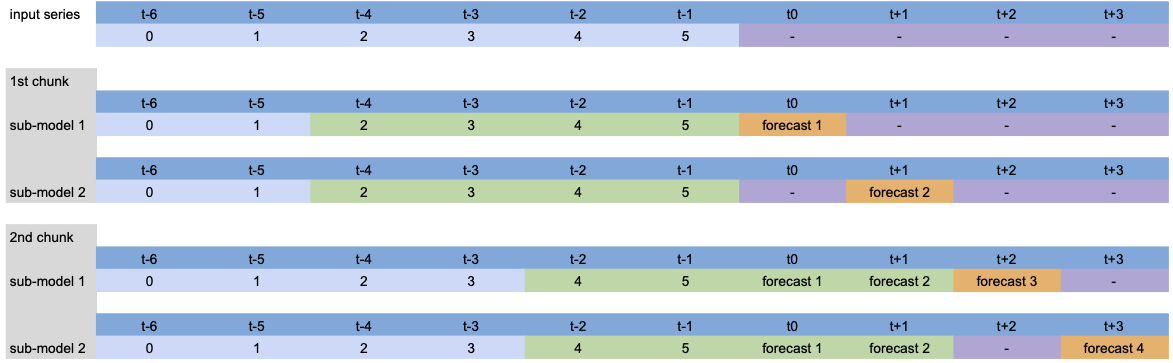
由于 n>output_chunk_length，模型必须使用自回归，预测期由两个大小为 output_chunk_length 的块组成。每个输出块没有滞后偏移，因为 multi_models=True。

模型设置: LinearRegressionModel(lags=[-4, -3, -2, -1], output_chunk_length=2, multi_models=False).

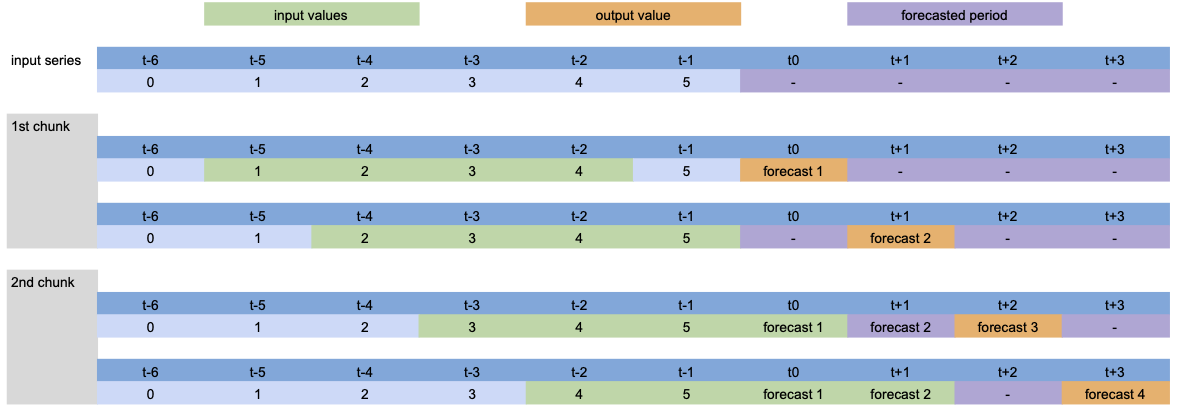
除了自回归预测外，我们可以看到滞后随着每个预测时间步的变化而变化，因为 multi_models=False。

在模型训练的表格化过程中，同样的过程也会发生：每个绿色块与一个橙色值配对，构成训练数据集。

概率预测

要将模型设为概率性模型，在创建 RegressionModel 时将参数 likelihood 设置为 quantile 或 poisson。在预测时，概率性模型可以： - 当 num_samples > 1 时，使用蒙特卡罗采样基于拟合的分布参数生成样本 - 当 predict_likelihood_parameters=True 时，返回拟合的分布参数

请注意，当使用 quantile 回归器时，每个分位数将由不同的模型拟合。

概率模型在每次调用 predict() 时，如果 num_samples > 1，将会生成不同的预测结果。为了获得可重复的结果，请在创建模型时设置随机种子，并按完全相同的顺序调用方法。

model = XGBModel(
    lags=24, output_chunk_length=1, likelihood="quantile", quantiles=[0.05, 0.5, 0.95]
)

model.fit(ts_energy_train)

pred_samples = model.predict(n=24, num_samples=200)
pred_params = model.predict(n=1, num_samples=1, predict_likelihood_parameters=True)

for val, comp in zip(pred_params.values()[0], pred_params.components):
    print(f"{comp} : {round(val, 3)}")

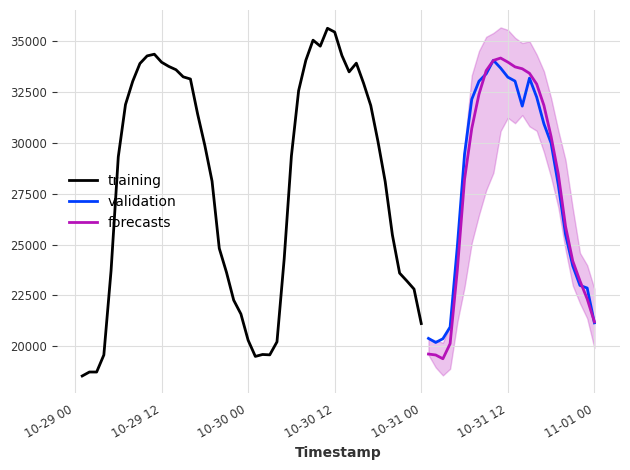
ts_energy_train[-48:].plot(label="training")
ts_energy_val[:24].plot(label="validation")
pred_samples.plot(label="forecasts")
plt.tight_layout()

Value_NE5_q0.05 : 19580.123046875
Value_NE5_q0.50 : 19623.302734375
Value_NE5_q0.95 : 20418.7421875

MultiOutputRegressor 包装器

一些回归模型支持原生的多输出支持。这对于拟合和预测是必需的：- 多个输出/多个目标步骤（使用 output_chunk_length>1 和 multi_models=True）- 使用分位数回归的概率模型 - 多变量序列

对于不支持此功能的模型，Darts 会在其周围包装 sklearn 的 MultiOutputRegressor 来处理底层的逻辑。

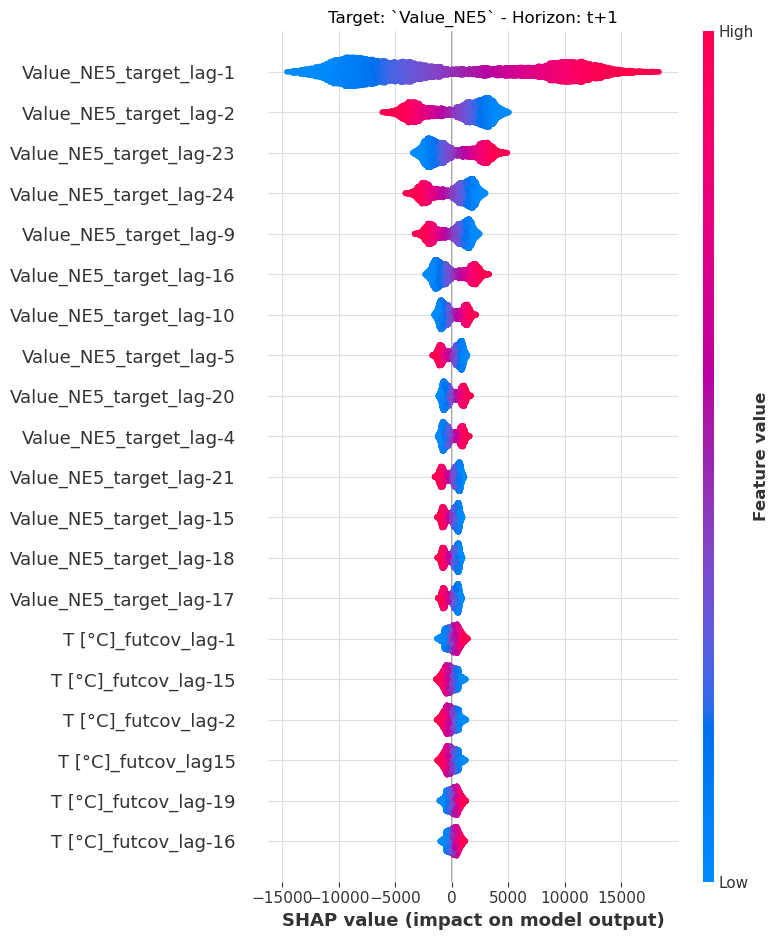
可解释性

我们通过 Darts 的 ShapExplainer 为回归模型提供可解释性。解释器使用基于博弈论的 shap 库，为我们预测的时间范围提供特征重要性的见解。

model = LinearRegressionModel(lags=24, lags_future_covariates=(24, 24))
model.fit(ts_energy_train, future_covariates=ts_weather)
shap_explainer = ShapExplainer(model=model)
shap_values = shap_explainer.summary_plot()

No data for colormapping provided via 'c'. Parameters 'vmin', 'vmax' will be ignored

# extracting the end of each series to reduce computation time
foreground_target = ts_energy_train[-24 * 2 :]
foreground_future_cov = ts_weather[foreground_target.start_time() :]

shap_explainer.force_plot_from_ts(
    foreground_series=foreground_target,
    foreground_future_covariates=foreground_future_cov,
)

# the plot cannot be rendered on GitHub or the Documentation page. Run it locally to see it.

Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.

结论

通过表格化数据并在库之间统一API，Darts 弥合了传统回归问题与时间序列预测之间的差距。

RegressionModel 及其子类提供了广泛的功能，只需几行代码就可以构建强大的模型。

附录

回归模型

RegressionModel 将 Darts API 包装在任何 sklearn 回归模型周围。通过这个，我们可以像使用任何其他 Darts 预测模型一样使用该模型。

作为一个例子，在示例数据集上拟合贝叶斯岭回归只需要几行代码：

model = RegressionModel(
    lags=24,
    lags_future_covariates=(48, 24),
    model=BayesianRidge(),
    output_chunk_length=24,
)

model.fit(ts_energy_train, future_covariates=ts_weather)

pred = model.predict(n=24)

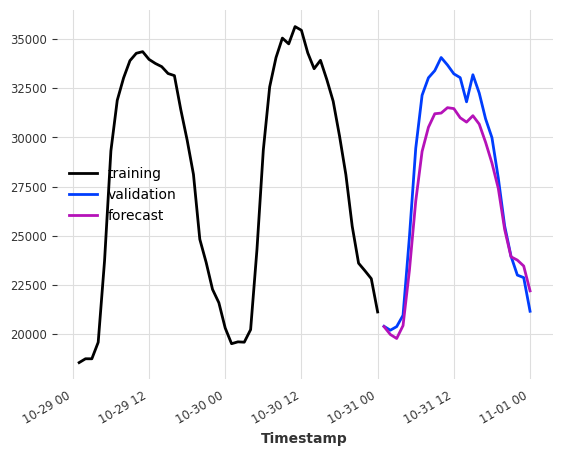
ts_energy_train[-48:].plot(label="training")
ts_energy_val[:24].plot(label="validation")
pred.plot(label="forecast")

<Axes: xlabel='Timestamp'>

底层模型方法仍然可以访问，通过将 BasesianRidge.coef_ 属性与 RegressionModel.lagged_feature_names 属性结合，可以轻松解释回归模型的系数：

# extract the coefficients of the first timestemp estimator
coef_values = model.model.estimators_[0].coef_
# get the lagged features name
coef_names = model.lagged_feature_names
# combine them in a dict
coefficients = {name: val for name, val in zip(coef_names, coef_values)}
# see the coefficient of the target value at last timestep before the forecasted period
{c_name: c_val for idx, (c_name, c_val) in enumerate(coefficients.items()) if idx < 5}

{'Value_NE5_target_lag-24': -0.3195560563281926,
 'Value_NE5_target_lag-23': 0.37621876784175745,
 'Value_NE5_target_lag-22': 0.005325414282057739,
 'Value_NE5_target_lag-21': -0.11885377506043901,
 'Value_NE5_target_lag-20': 0.12892167797527437}

RegressionModel 类的一个限制是它没有提供开箱即用的概率预测，但可以通过创建一个继承自 RegressionModel 和 _LikelihoodMixin 的新类并实现缺失的方法来实现（LinearRegressionModel 类可以用作模板）。

自定义模型

只要模型能处理表格数据并提供 fit() 和 predict() 方法，你甚至可以实现自己的模型：

class CustomRegressionModel:
    def __init__(self, weights: np.ndarray):
        """Barebone weighted average"""
        self.weights = weights
        self.norm_coef = sum(weights)

    def fit(self, X: np.ndarray, y: np.ndarray, *args, **kwargs):
        return self

    def predict(self, X: np.ndarray):
        """Apply weights on each sample"""
        return (
            np.stack([np.correlate(x, self.weights, mode="valid") for x in X])
            / self.norm_coef
        )

    def get_params(self, deep: bool):
        return {"weights": self.weights}


window_weights = np.arange(1, 25, 1) ** 2
model = RegressionModel(
    lags=24,
    output_chunk_length=24,
    model=CustomRegressionModel(window_weights),
    multi_models=False,
)
model.fit(ts_energy_train)
pred = model.predict(n=24)

ts_energy_train[-48:].plot(label="training")
ts_energy_val[:24].plot(label="validation")
pred.plot(label="forecast")

<Axes: xlabel='Timestamp'>

提升树模型的示例

确保已安装 lightgbm 和 catboost 的依赖项。您可以查看我们的安装指南 这里

lgbm_model = LightGBMModel(lags=24, output_chunk_length=24, verbose=0)
xgboost_model = XGBModel(lags=24, output_chunk_length=24)
catboost_model = CatBoostModel(lags=24, output_chunk_length=24)

lgbm_model.fit(ts_energy_train)
xgboost_model.fit(ts_energy_train)
catboost_model.fit(ts_energy_train)

pred_lgbm = lgbm_model.predict(n=24)
pred_xgboost = xgboost_model.predict(n=24)
pred_catboost = catboost_model.predict(n=24)

print(f"LightGBMModel MAPE: {mape(ts_energy_val, pred_lgbm)}")
print(f"XGBoostModel MAPE: {mape(ts_energy_val, pred_xgboost)}")
print(f"CatboostModel MAPE: {mape(ts_energy_val, pred_catboost)}")

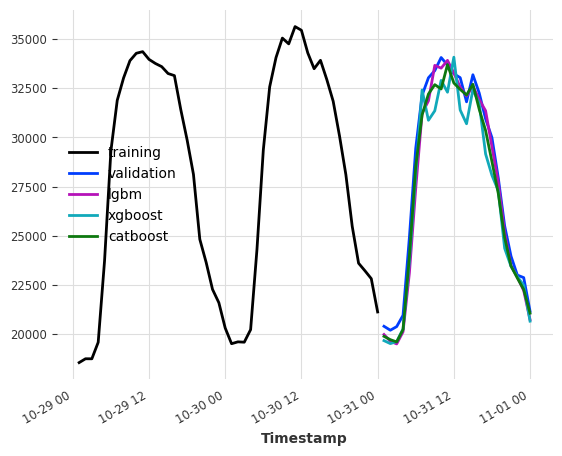
ts_energy_train[-48:].plot(label="training")
ts_energy_val[:24].plot(label="validation")
pred_lgbm.plot(label="lgbm")
pred_xgboost.plot(label="xgboost")
pred_catboost.plot(label="catboost")

LightGBMModel MAPE: 2.2682070257112743
XGBoostModel MAPE: 3.5364068635935895
CatboostModel MAPE: 2.373275454432286

<Axes: xlabel='Timestamp'>

上一页

电力负荷预测的超参数优化

下一页

快速傅里叶变换预测模型 (FFT)