使用 darts 过滤器进行过滤和预测

在这个笔记本中，我们将研究卡尔曼滤波算法如何用于提高受噪声影响的数据质量。白噪声是任何类型传感器获取的数据中的常见成分。

卡尔曼滤波器在Darts中是一种不同类型的模型，因为它是一个 FilteringModel （而不是 ForecastingModel ），可以用来平滑序列。在卡尔曼滤波器的情况下，观测值的“实际”潜在值是使用线性动态系统的状态空间模型推断出来的。这个系统可以作为输入提供，也可以在数据上进行拟合。

在这个笔记本中，我们将生成一个简单的合成数据集，并看看如何使用卡尔曼滤波器来去噪。请注意，这是一个玩具示例，主要是为了展示Darts卡尔曼滤波器API的工作原理。

%reload_ext autoreload
%autoreload 2
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

from darts import TimeSeries
from darts.models import KalmanFilter
from darts.utils import timeseries_generation as tg

一阶系统的阶跃响应

在测量中常见的一种信号形状是指数趋近于稳态，例如在系统趋近于设定点的过程中。我们首先准备输入（控制信号）和输出，并添加噪声以获得真实的观测数据。

NOISE_DISTANCE = 0.1
SAMPLE_SIZE = 200
np.random.seed(42)

# Prepare the input
u = TimeSeries.from_values(np.heaviside(np.linspace(-5, 10, SAMPLE_SIZE), 0))

# Prepare the output
y = u * TimeSeries.from_values(1 - np.exp(-np.linspace(-5, 10, SAMPLE_SIZE)))

# Add white noise to obtain the observations
noise = tg.gaussian_timeseries(length=SAMPLE_SIZE, std=NOISE_DISTANCE)
y_noise = y + noise

plt.figure(figsize=[12, 8])
u.plot(label="Input")
y.plot(color="gray", label="Output")
y_noise.plot(color="red", label="Noisy observations")
plt.legend()
plt.show()

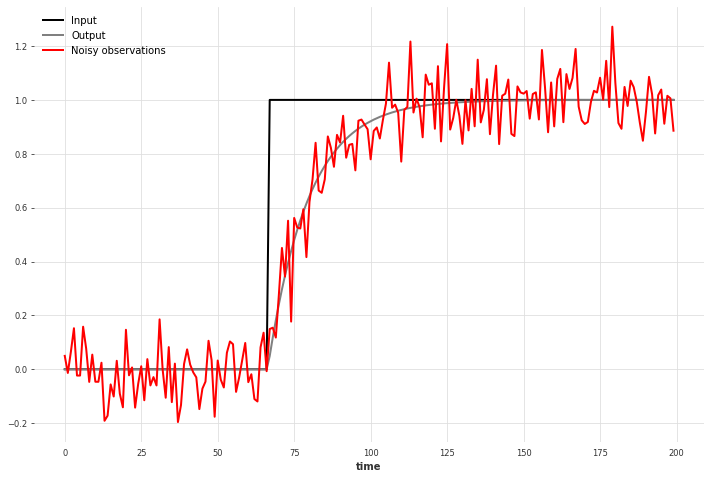
这种行为可以通过一个一阶线性动态系统来建模，使其成为带有 dim_x=1 的卡尔曼滤波器的理想候选。

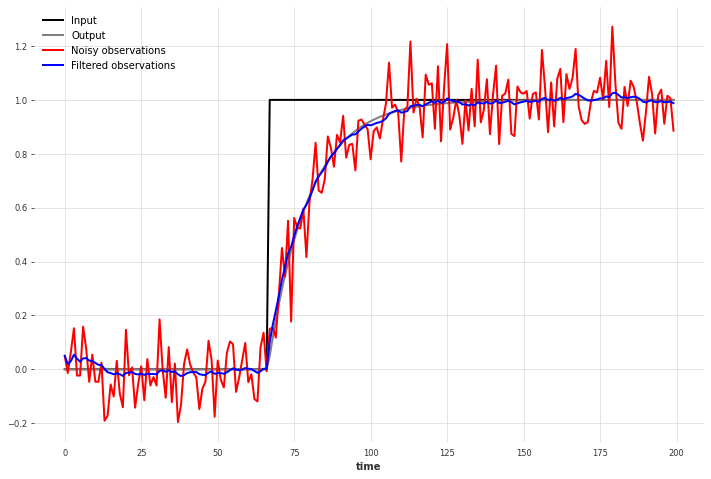
我们使用输入作为协变量来拟合卡尔曼滤波器，并对相同的时间序列进行滤波。请注意，如果我们使用更长的时间序列来拟合模型，结果可能会更好。

过滤后的观测值与无噪声的输出信号相当接近，并且在输入发生阶跃变化时特别能跟踪输出。如果是移动平均等过滤方法，情况就不会是这样，这表明模型确实考虑了输入（协变量）。

我们可以观察到，时间序列开始时的误差较大，因为卡尔曼滤波器在那个时间点几乎没有信息来估计状态。

kf = KalmanFilter(dim_x=1)
kf.fit(y_noise, u)
y_filtered = kf.filter(y_noise, u)

plt.figure(figsize=[12, 8])
u.plot(label="Input")
y.plot(color="gray", label="Output")
y_noise.plot(color="red", label="Noisy observations")
y_filtered.plot(color="blue", label="Filtered observations")
plt.legend()

<matplotlib.legend.Legend at 0x7fc594431ed0>

我们还可以通过增加 num_samples 来获得潜在值的概率估计。

y_filtered = kf.filter(y_noise, u, num_samples=1000)

plt.figure(figsize=[12, 8])
u.plot(label="Input")
y.plot(color="gray", label="Output")
y_noise.plot(color="red", label="Noisy observations")
y_filtered.plot(color="blue", label="Filtered observations")
plt.legend()

<matplotlib.legend.Legend at 0x7fc581075190>

螺旋绘图

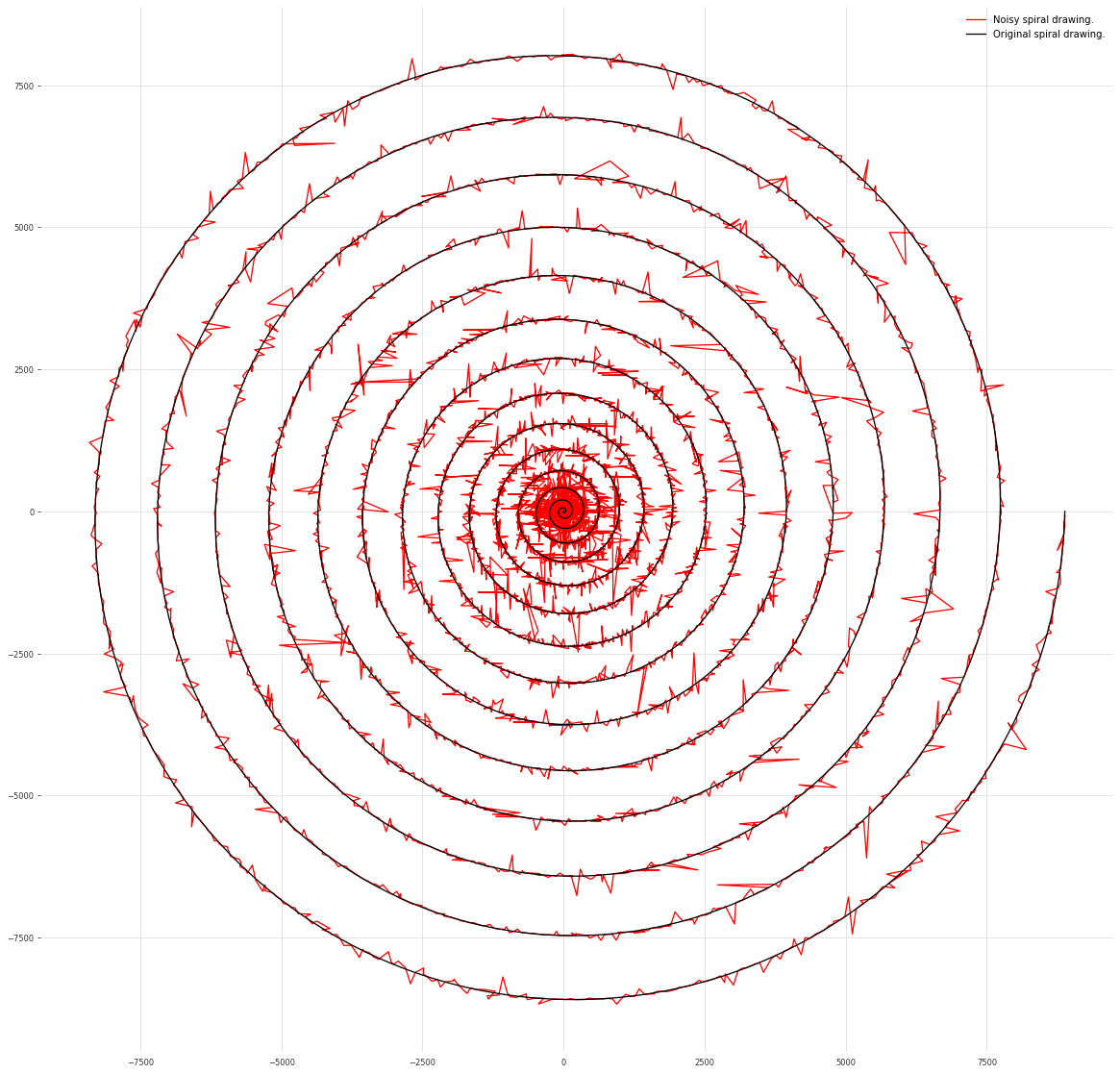
首先，让我们生成一个简单的图形，并为其添加显著的白噪声。

NOISE_DISTANCE = 0.5
SAMPLE_SIZE = 10000
RESIZE_NOISE = 150

# Prepare the drawing
theta = np.radians(np.linspace(360 * 15, 0, SAMPLE_SIZE))
r = theta**2
x_2 = r * np.cos(theta)
y_2 = r * np.sin(theta)

# add white noise (gaussian noise, can be mapped from the random distribution using rand**3)
# and resize to RESIZE_NOISE
x_2_noise = x_2 + (np.random.normal(0, NOISE_DISTANCE, SAMPLE_SIZE) ** 3) * RESIZE_NOISE
y_2_noise = y_2 + (np.random.normal(0, NOISE_DISTANCE, SAMPLE_SIZE) ** 3) * RESIZE_NOISE

plt.figure(figsize=[20, 20])
plt.plot(x_2_noise, y_2_noise, color="red", label="Noisy spiral drawing.")
plt.plot(x_2, y_2, label="Original spiral drawing.")
plt.legend()
plt.show()

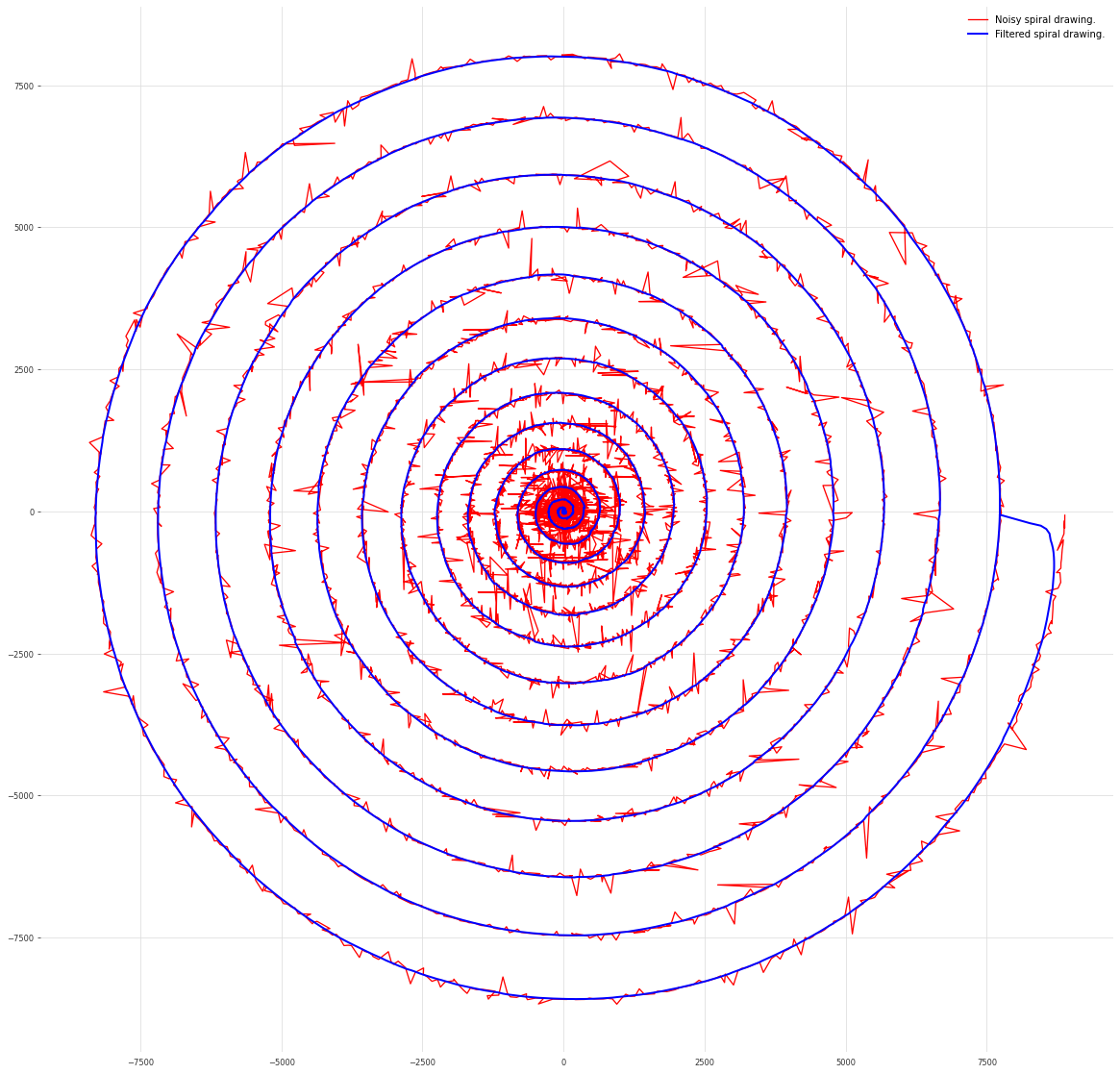
上述绘图可以通过一个无输入的二阶线性动力系统生成（衰减至其在 (0, 0) 处的平衡点）。因此，我们可以在包含“x”和“y”分量的多元时间序列上拟合一个 dim_x=2 的卡尔曼滤波器。我们看到，卡尔曼滤波器在去噪螺旋绘图方面做得很好。

注意，我们必须调整参数 num_block_rows 以使模型拟合收敛。

kf = KalmanFilter(dim_x=2)
ts = TimeSeries.from_values(x_2_noise).stack(TimeSeries.from_values(y_2_noise))
kf.fit(ts, num_block_rows=50)

filtered_ts = kf.filter(ts).values()
filtered_x = filtered_ts[:, 0]
filtered_y = filtered_ts[:, 1]

plt.figure(figsize=[20, 20])
plt.plot(x_2_noise, y_2_noise, color="red", label="Noisy spiral drawing.")
plt.plot(
    filtered_x, filtered_y, color="blue", linewidth=2, label="Filtered spiral drawing."
)
plt.legend()

<matplotlib.legend.Legend at 0x7fc58144a950>

上一页

模型集成

下一页

使用高斯过程滤波器进行过滤和预测