动态时间规整 (DTW)¶
以下展示了 darts 中 DTW 模块的功能。动态时间规整允许你比较两个长度和时间轴不同的时序数据。该算法将确定两个序列中元素之间的最佳对齐方式,使得它们之间的成对距离最小化。
[1]:
# fix python path if working locally
from utils import fix_pythonpath_if_working_locally
fix_pythonpath_if_working_locally()
[2]:
%load_ext autoreload
%autoreload 2
%matplotlib inline
from darts.dataprocessing import dtw
from darts.utils import timeseries_generation as tg
from darts.utils.missing_values import fill_missing_values
from darts.datasets import SunspotsDataset
from darts.timeseries import TimeSeries
from darts.metrics import dtw_metric, mae, mape
from darts.models import MovingAverageFilter
from scipy.signal import argrelextrema
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
[3]:
SMALL_SIZE = 30
MEDIUM_SIZE = 35
BIGGER_SIZE = 40
FIG_WIDTH = 20
FIG_SIZE = (40, 10)
plt.rc("font", size=SMALL_SIZE) # controls default text sizes
plt.rc("axes", titlesize=SMALL_SIZE) # fontsize of the axes title
plt.rc("axes", labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc("xtick", labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc("ytick", labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc("legend", fontsize=SMALL_SIZE) # legend fontsize
plt.rc("figure", titlesize=BIGGER_SIZE) # fontsize of the figure title
plt.rc("figure", figsize=FIG_SIZE) # size of the figure
读取与格式化¶
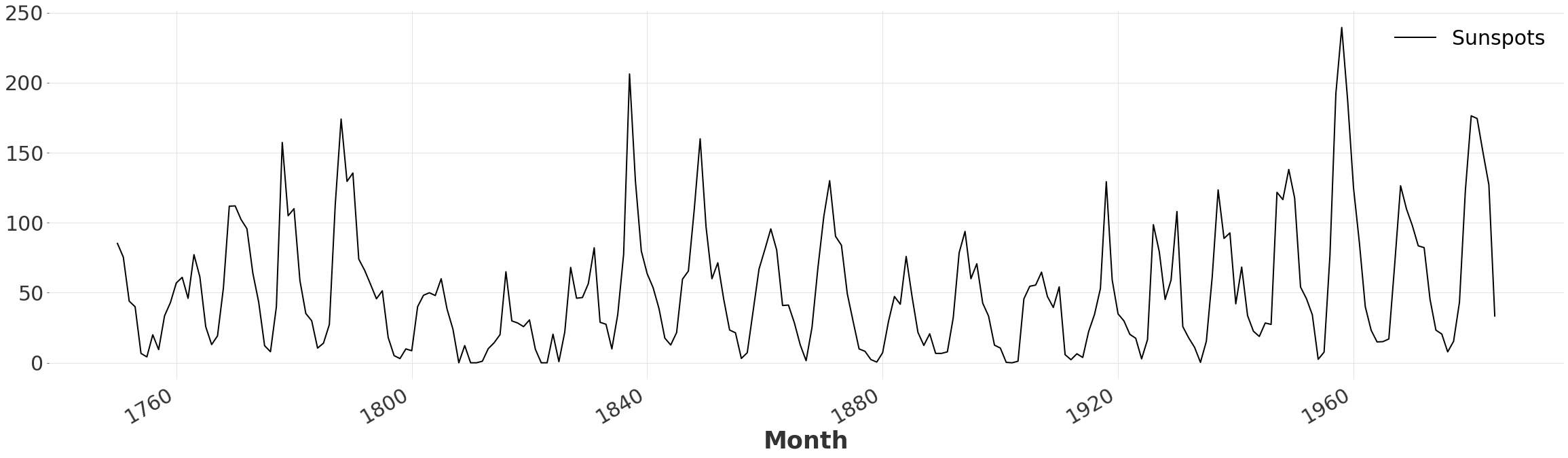
这里我们简单地读取包含太阳黑子数量的CSV文件,并将这些值转换为所需格式。我们对数据集进行重采样以消除高频噪声,因为我们只对总体形状感兴趣。
[4]:
ts = SunspotsDataset().load()
ts = ts.resample(freq="y")
ts.plot()
确定峰值的数量¶
我们观察到该序列由一系列尖锐的波峰和波谷组成。让我们快速确定要考虑的周期数。我们首先对该序列应用移动平均滤波器,以消除虚假的局部最大值。然后我们简单地计算由 argrelextrema 返回的局部最大值的数量。
[5]:
ts_smooth = MovingAverageFilter(window=3).filter(ts)
minimums = argrelextrema(ts_smooth.univariate_values(), np.greater)
periods = len(minimums[0])
periods
[5]:
24
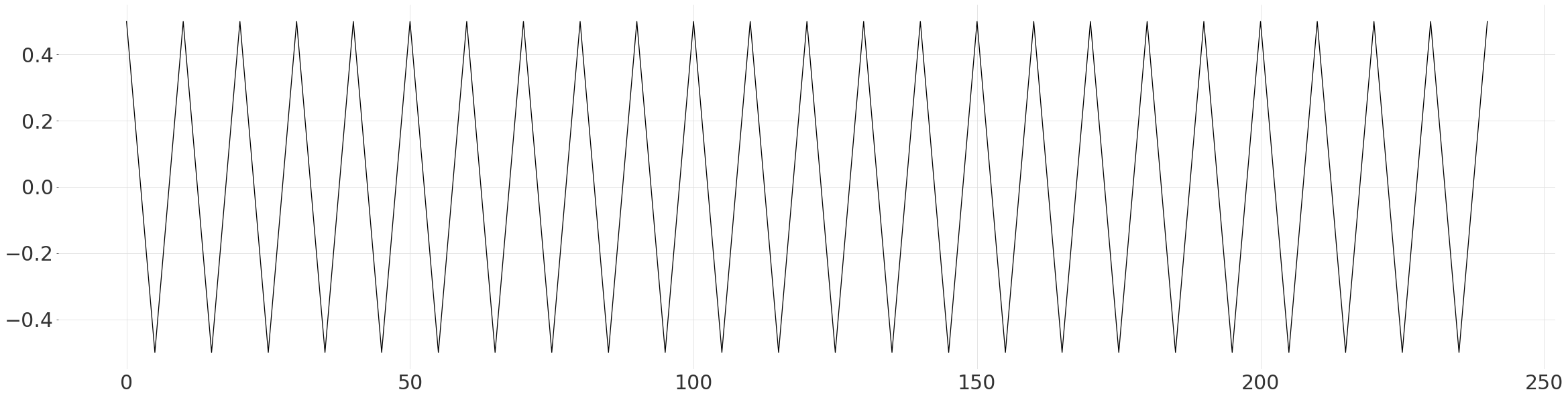
生成一个用于比较的模式¶
在这里,我们简单地基于之前的观察,构建了一个简化的模式,即线性峰值和谷值。我们确保均值为0,范围为1,以便更容易拟合数据。
[6]:
steps = int(np.ceil(len(ts) / (periods * 2)))
down = np.linspace(0.5, -0.5, steps + 1)[:-1]
up = np.linspace(-0.5, 0.5, steps + 1)[:-1]
values = np.append(np.tile(np.append(down, up), periods), 0.5)
plt.plot(np.arange(len(values)), values)
将模式拟合到序列¶
我们将数据重新缩放并移动,使其与实际系列一致。然后我们创建一个新的 TimeSeries ,其时间轴与太阳黑子数据集相同。虽然这不是执行动态时间规整的必要条件,但它将使我们能够绘制并比较初始对齐。由于我们的模式比太阳黑子时间序列本身略长,我们丢弃了结束日期之后的所有值。
[7]:
m = 90
c = 55
scaled_values = values * m + c
time_range = pd.date_range(start=ts.start_time(), freq="y", periods=len(values))
ts_shape_series = pd.Series(scaled_values, index=time_range, name="Shape")
ts_shape = TimeSeries.from_series(ts_shape_series)
ts_shape = ts_shape.drop_after(ts.end_time())
ts_shape.plot()
ts.plot()
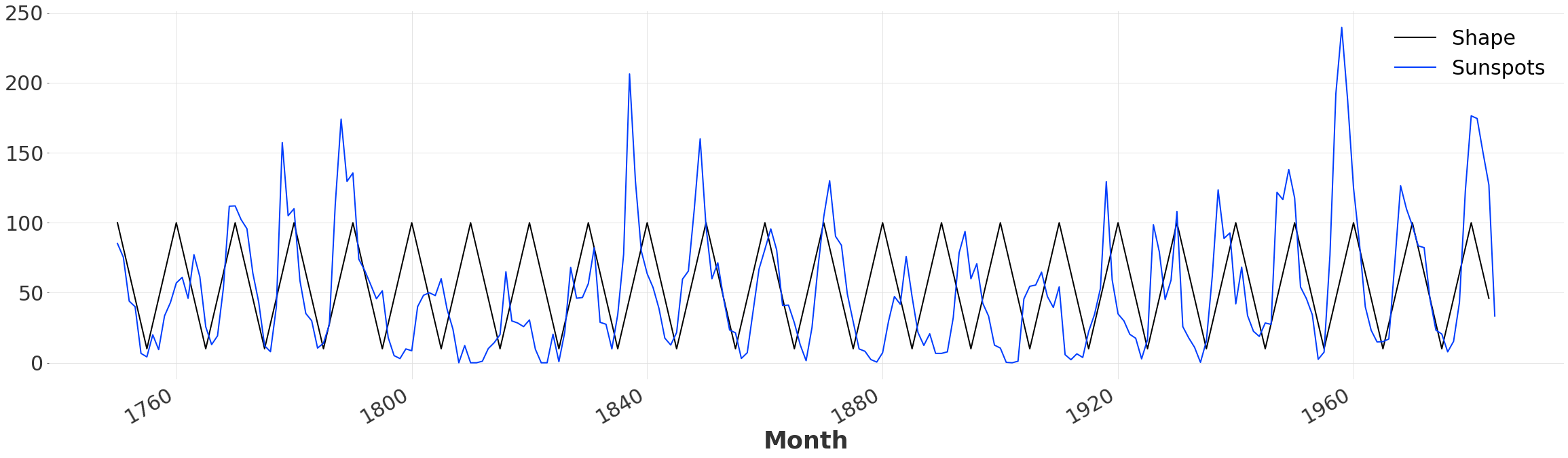
定量比较¶
我们可以使用平均绝对误差,也称为 mae,来评估我们的简单模式与数据的拟合程度。从上图可以看出,峰值之间的时间存在一些波动,导致错位和相对较高的误差。
[8]:
original_mae = mae(ts, ts_shape)
original_mae
[8]:
34.01837606837607
进入动态时间规整¶
幸运的是,找到两个序列之间的最佳对齐正是DTW的设计目的!我们只需要用两个时间序列调用dtw。
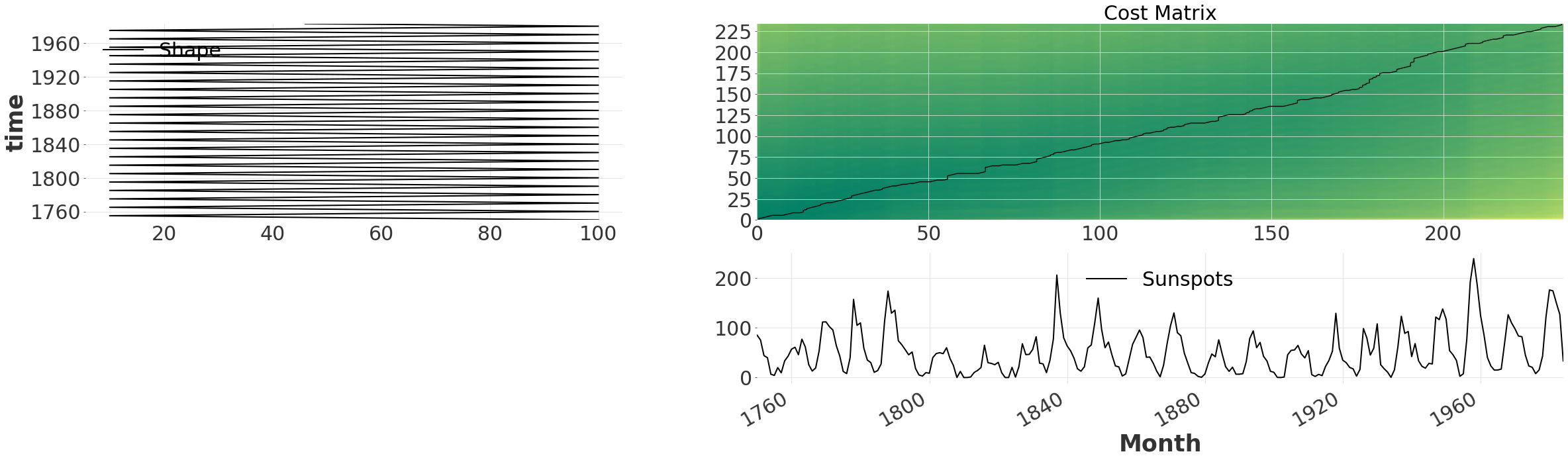
无窗口¶
默认行为是考虑时间序列之间所有可能的对齐方式。当我们使用 .plot() 绘制成本矩阵以及路径时,这一点变得显而易见。成本矩阵表示将 (i,j) 匹配在一起的对齐的总成本/距离。对于我们的时间序列,我们观察到一条深绿色带穿过对角线。这表明两个时间序列从一开始就基本上是对齐的。
[9]:
exact_alignment = dtw.dtw(ts, ts_shape)
exact_alignment.plot(show_series=True)
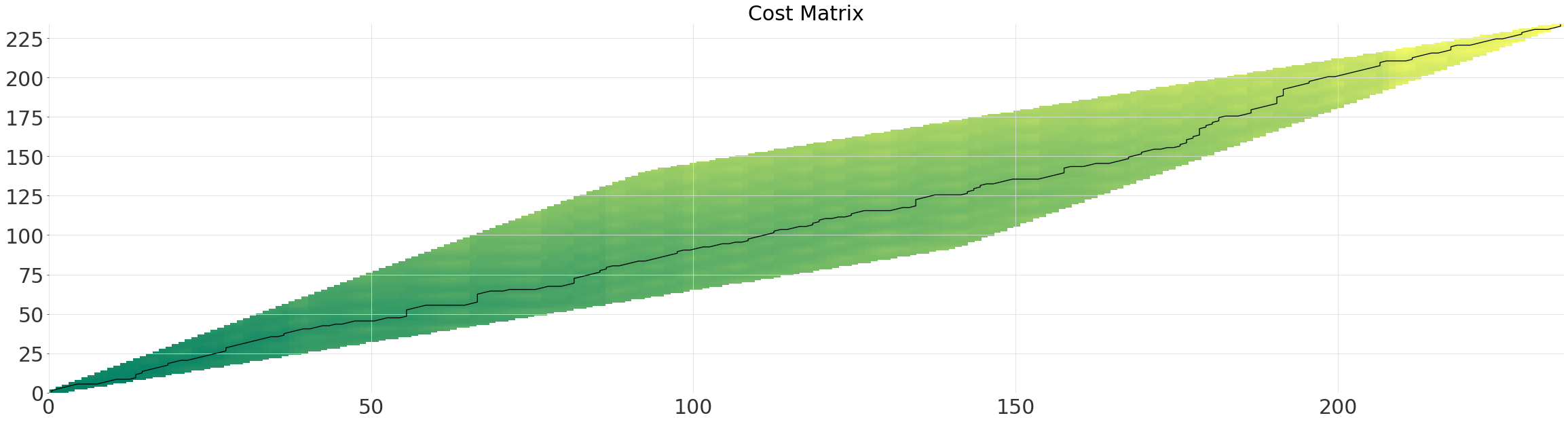
多重网格¶
在大数据集上快速计算所有可能的对齐方式在计算上变得非常昂贵(二次复杂度)。
相反,我们可以使用多网格求解器,它在近似线性时间内运行。该求解器首先在较小的网格上确定最佳路径,然后递归地重新投影和细化路径,每次将分辨率加倍。只需启用多网格求解器(线性复杂度)通常会导致速度大幅提升,而不会损失太多精度。
参数 multi_grid_radius 控制从较低分辨率找到的路径延伸搜索窗口的程度。换句话说,通过增加它,你以性能为代价获得了更高的精度。
[10]:
multi_grid_radius = 10
multigrid_alignment = dtw.dtw(ts, ts_shape, multi_grid_radius=multi_grid_radius)
multigrid_alignment.plot()
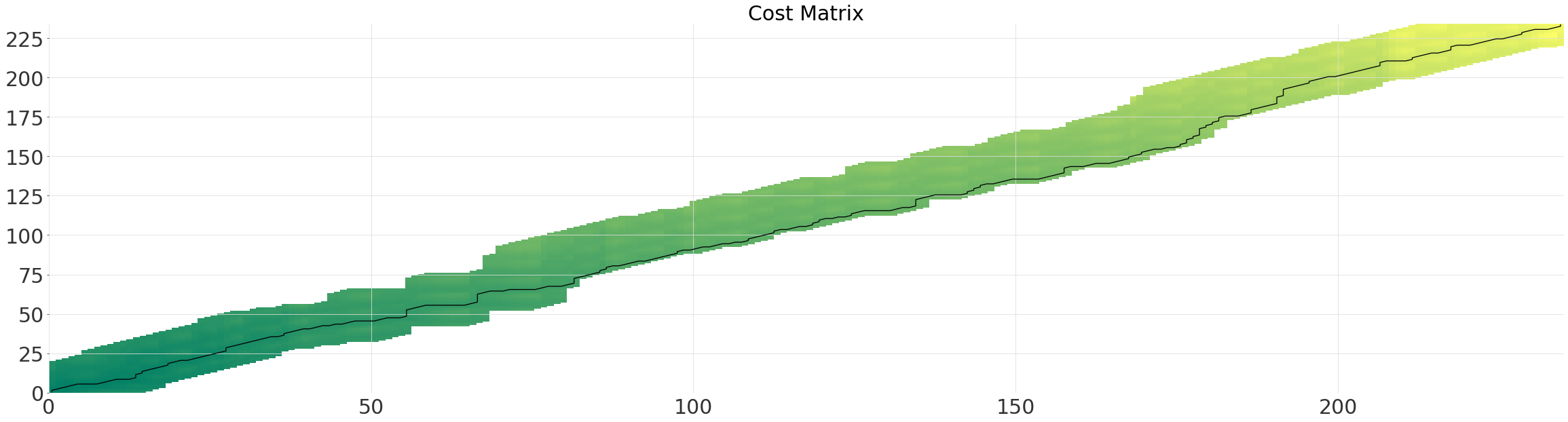
对角窗口 (SakoeChiba)¶
SakoeChiba窗口形成一个由``window_size``参数决定的斜带。当你知道两个时间序列已经大部分对齐或者想要限制扭曲量时,这个窗口效果最佳。它将确保一个序列中的元素n仅与另一个序列中的元素n-window_size匹配。
[11]:
sakoechiba_alignment = dtw.dtw(ts, ts_shape, window=dtw.SakoeChiba(window_size=10))
sakoechiba_alignment.plot()
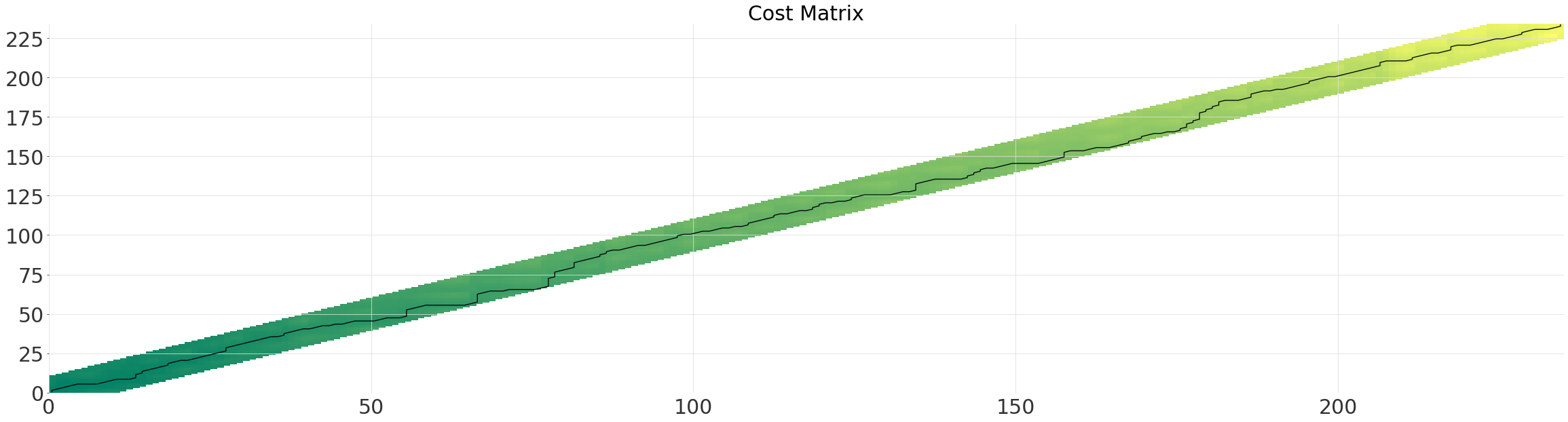
平行四边形窗口 (Itakura)¶
参数 max_slope 控制平行四边形较陡一侧的斜率。对于我们的时间序列,窗口有些浪费,因为最佳路径并没有显著偏离对角线。
[12]:
itakura_alignment = dtw.dtw(ts, ts_shape, window=dtw.Itakura(max_slope=1.5))
itakura_alignment.plot()
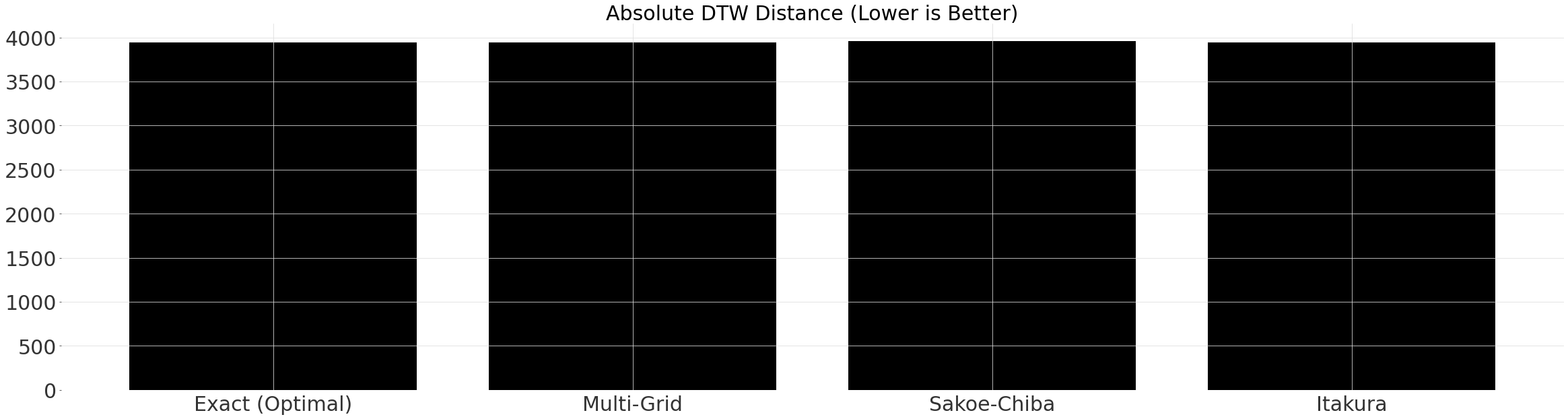
不同对齐方式的比较¶
尽管每个窗口的运行时间会有所不同,但路径的长度实际上是相同的。如果我们进一步约束窗口或减少 multi_grid_radius,我们会发现最优路径比其他路径更短。
[13]:
alignments = [
exact_alignment,
multigrid_alignment,
sakoechiba_alignment,
itakura_alignment,
]
names = ["Exact (Optimal)", "Multi-Grid", "Sakoe-Chiba", "Itakura"]
distances = [align.distance() for align in alignments]
plt.title("Absolute DTW Distance (Lower is Better)")
plt.bar(names, distances)
alignment = multigrid_alignment
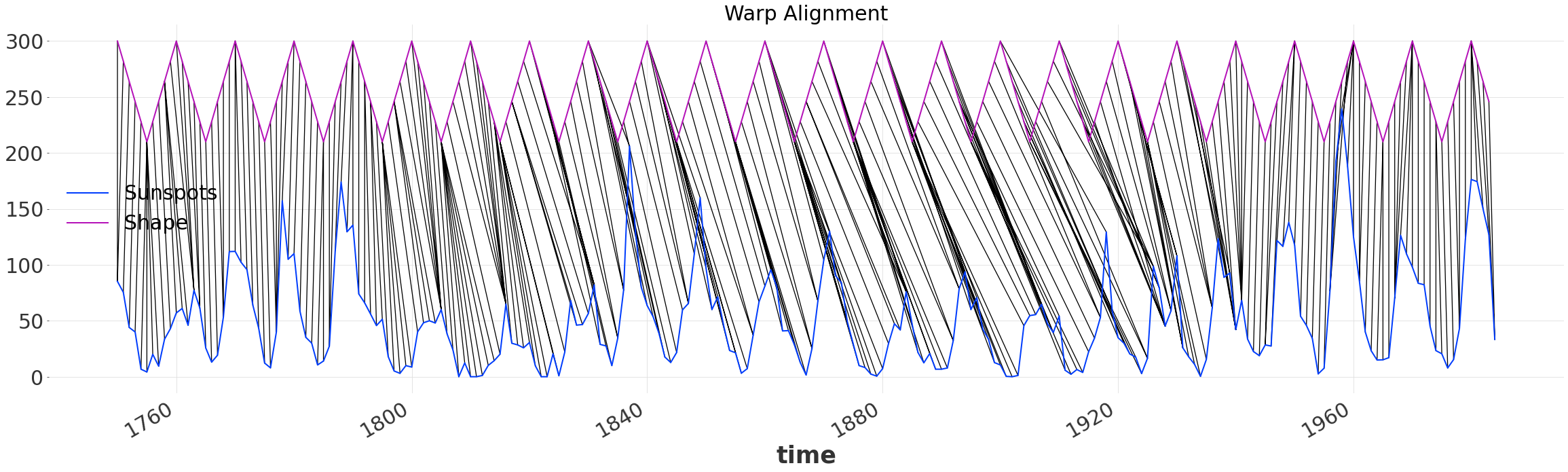
可视化对齐¶
[14]:
alignment.plot_alignment(series2_y_offset=200)
plt.gca().set_title("Warp Alignment")
扭曲的时间序列¶
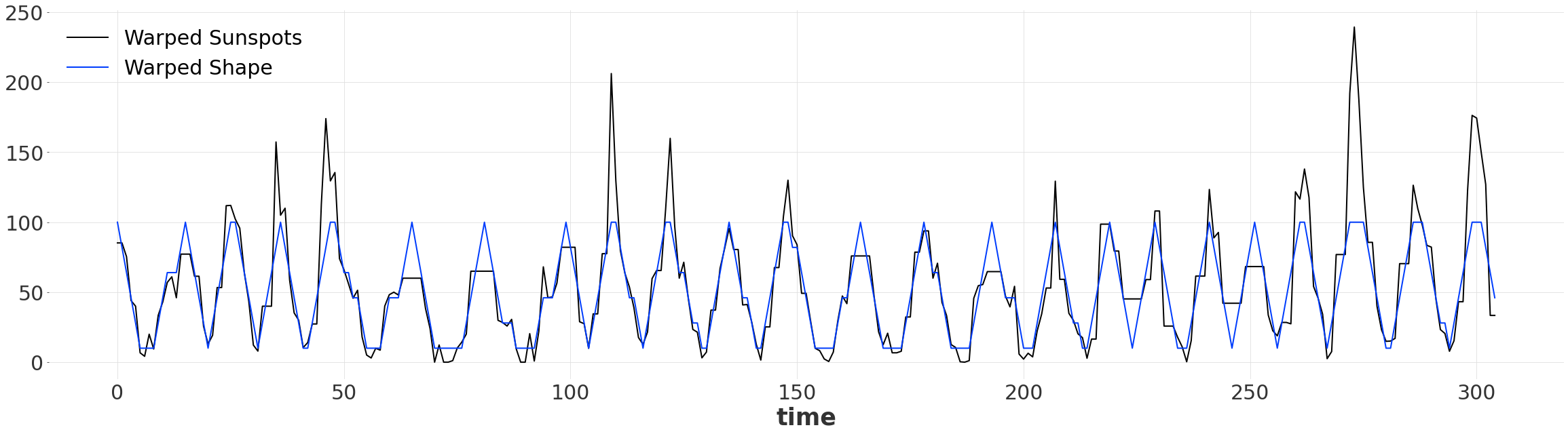
一旦我们找到了一个对齐方式,我们就可以生成两个长度相同的时间扭曲序列。由于我们已经扭曲了时间维度,默认情况下,新的扭曲序列由 pd.RangeIndex 索引。现在,尽管原始序列并不匹配,我们的简单模式与序列对齐了!
[15]:
warped_ts, warped_ts_shape = alignment.warped()
warped_ts.plot(label="Warped Sunspots")
warped_ts_shape.plot(label="Warped Shape")
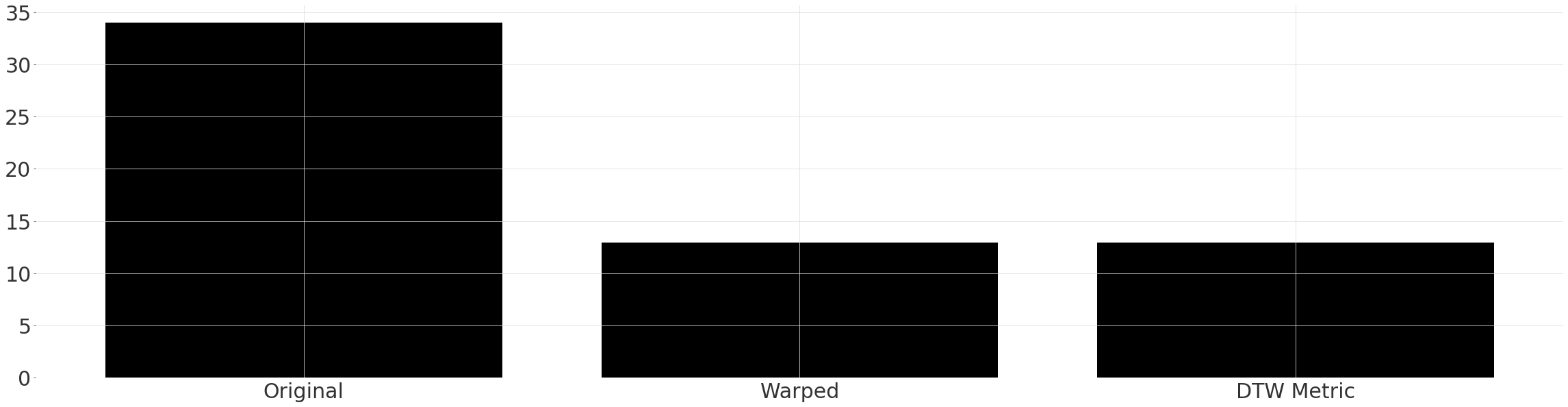
定量比较¶
我们再次应用 mae 指标,但这次是针对我们扭曲后的序列。如果我们只对扭曲后的相似性感兴趣,我们也可以直接调用辅助函数 dtw_metric。注意扭曲序列之间的误差减少了约65%!
[16]:
warped_mae0 = mae(warped_ts, warped_ts_shape)
warped_mae1 = dtw_metric(ts, ts_shape, metric=mae, multi_grid_radius=multi_grid_radius)
plt.bar(["Original", "Warped", "DTW Metric"], [original_mae, warped_mae0, warped_mae1])
查找匹配的子序列¶
根据对齐方式,我们可以找到两个时间序列的匹配子序列。
两个元素之间的差异小于某个阈值
原始图案未被扭曲
子序列具有一定的最小长度
[17]:
THRESHOLD = 20
MATCH_MIN_LENGTH = 5
path = alignment.path()
path = path.reshape((-1,))
warped_ts_values = warped_ts.univariate_values()
warped_ts_shape_values = warped_ts_shape.univariate_values()
within_threshold = (
np.abs(warped_ts_values - warped_ts_shape_values) < THRESHOLD
) # Criterion 1
linear_match = np.diff(path[1::2]) == 1 # Criterion 2
matches = np.logical_and(within_threshold, np.append(True, linear_match))
if not matches[-1]:
matches = np.append(matches, False)
matched_ranges = []
match_begin = 0
last_m = False
for i, m in enumerate(matches):
if last_m and not m:
match_end = i - 1
match_len = match_end - match_begin
if match_len >= MATCH_MIN_LENGTH: # Criterion 3
matched_ranges.append(pd.RangeIndex(match_begin, i - 1))
if not last_m and m:
match_begin = i
last_m = m
matched_ranges
[17]:
[RangeIndex(start=0, stop=5, step=1),
RangeIndex(start=16, stop=23, step=1),
RangeIndex(start=27, stop=33, step=1),
RangeIndex(start=97, stop=108, step=1),
RangeIndex(start=115, stop=121, step=1),
RangeIndex(start=131, stop=138, step=1),
RangeIndex(start=174, stop=180, step=1),
RangeIndex(start=218, stop=223, step=1),
RangeIndex(start=252, stop=258, step=1)]
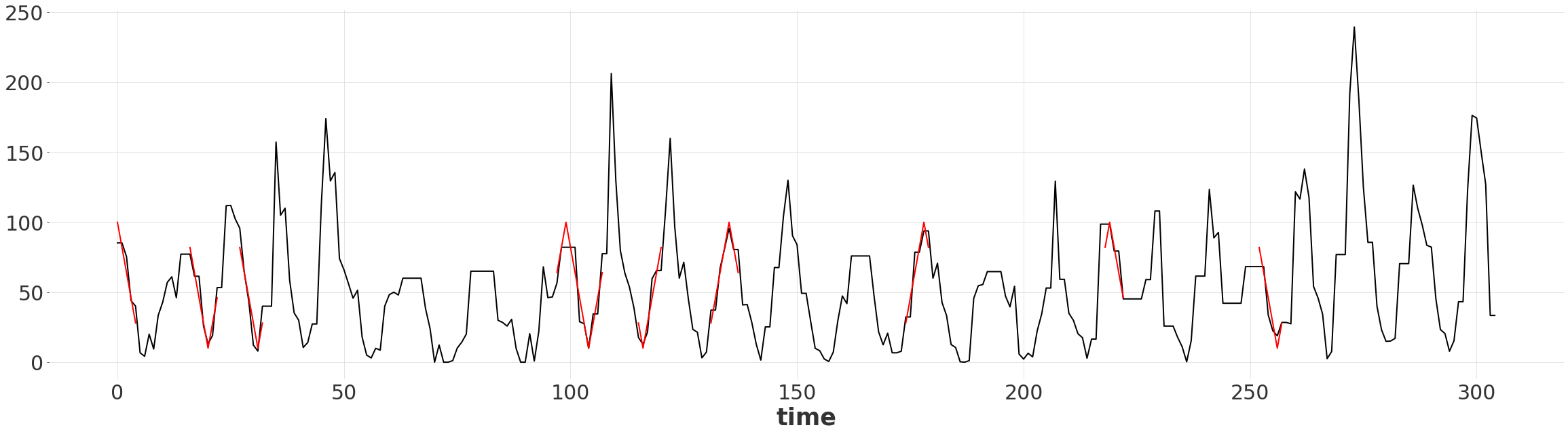
可视化匹配的子序列¶
我们可以通过 RangeIndex 简单地对扭曲的形状序列进行切片,以提取子序列。
[18]:
warped_ts.plot()
for r in matched_ranges:
warped_ts_shape[r].plot(color="red")
plt.gca().get_legend().remove()
[ ]: