时间融合变换器¶
在这个笔记本中,我们展示了两个如何使用 Darts 的 TFTModel 的示例。如果你是 darts 的新手,我们建议你首先跟随 快速开始 笔记本。
[1]:
# fix python path if working locally
from utils import fix_pythonpath_if_working_locally
fix_pythonpath_if_working_locally()
[2]:
%load_ext autoreload
%autoreload 2
%matplotlib inline
[3]:
import numpy as np
import pandas as pd
from tqdm import tqdm_notebook as tqdm
import matplotlib.pyplot as plt
from darts import TimeSeries, concatenate
from darts.dataprocessing.transformers import Scaler
from darts.models import TFTModel
from darts.metrics import mape
from darts.utils.statistics import check_seasonality, plot_acf
from darts.datasets import AirPassengersDataset, IceCreamHeaterDataset
from darts.utils.timeseries_generation import datetime_attribute_timeseries
from darts.utils.likelihood_models import QuantileRegression
import warnings
warnings.filterwarnings("ignore")
import logging
logging.disable(logging.CRITICAL)
时间融合变换器 (TFT)¶
Darts 的 TFTModel 包含了原始 Temporal Fusion Transformer (TFT) 架构中的以下主要组件,如 这篇论文 所述:
门控机制:跳过模型架构中未使用的组件
变量选择网络:在每个时间步选择相关的输入变量。
使用 LSTMs(长短期记忆)对过去和未来的输入进行时间处理
多头注意力机制:捕捉长期时间依赖关系
预测区间:默认情况下,生成的是分位数预测,而不是确定性值
训练¶
TFTModel 可以利用过去和未来的协变量进行训练。它按顺序在由编码器和解码器部分组成的固定大小的块上进行训练:
编码器:过去输入的
input_chunk_length过去目标:强制性
过去协变量:可选
解码器:未来已知输入,使用
output_chunk_length未来协变量:必填(如果没有可用,请考虑
TFTModel的可选参数add_encoders或add_relative_index来自 这里)
在每次迭代中,模型在解码器部分生成一个形状为 (output_chunk_length, n_quantiles) 的分位数预测。
预测¶
概率预测¶
默认情况下,TFTModel 使用 QuantileRegression 生成概率分位数预测。这给出了每个预测步骤中可能的目标值范围。Darts 中的大多数深度学习模型(包括 TFTModel)都支持 QuantileRegression 和其他 16 种似然性,通过在模型创建时设置 likelihood=MyLikelihood() 来生成概率预测。
为了产生有意义的结果,在预测时设置 num_samples >> 1。例如:
model.predict(*args, **kwargs, num_samples=200)
使用与训练时相同大小的编码器-解码器块,自动回归生成预测范围为 n 的预测。
如果 n > output_chunk_length,你需要为传递给 model.train() 的协变量提供额外的未来值。
确定性预测¶
要生成确定性而非概率性的预测,请在模型创建时将参数 likelihood 设置为 None ,并将 loss_fn 设置为 PyTorch 损失函数。例如:
model = TFTModel(*args, **kwargs, likelihood=None, loss_fn=torch.nn.MSELoss())
...
model.predict(*args, **kwargs, num_samples=1)
[4]:
# before starting, we define some constants
num_samples = 200
figsize = (9, 6)
lowest_q, low_q, high_q, highest_q = 0.01, 0.1, 0.9, 0.99
label_q_outer = f"{int(lowest_q * 100)}-{int(highest_q * 100)}th percentiles"
label_q_inner = f"{int(low_q * 100)}-{int(high_q * 100)}th percentiles"
航空乘客示例¶
这个数据集高度依赖于协变量。知道月份可以告诉我们很多关于季节性成分的信息,而年份则决定了趋势成分的影响。
此外,让我们将时间索引转换为整数值,并将它们也用作协变量。
所有三个协变量在将来都是已知的,并且可以作为 future_covariates 与 TFTModel 一起使用。
[5]:
# Read data
series = AirPassengersDataset().load()
# we convert monthly number of passengers to average daily number of passengers per month
series = series / TimeSeries.from_series(series.time_index.days_in_month)
series = series.astype(np.float32)
# Create training and validation sets:
training_cutoff = pd.Timestamp("19571201")
train, val = series.split_after(training_cutoff)
# Normalize the time series (note: we avoid fitting the transformer on the validation set)
transformer = Scaler()
train_transformed = transformer.fit_transform(train)
val_transformed = transformer.transform(val)
series_transformed = transformer.transform(series)
# create year, month and integer index covariate series
covariates = datetime_attribute_timeseries(series, attribute="year", one_hot=False)
covariates = covariates.stack(
datetime_attribute_timeseries(series, attribute="month", one_hot=False)
)
covariates = covariates.stack(
TimeSeries.from_times_and_values(
times=series.time_index,
values=np.arange(len(series)),
columns=["linear_increase"],
)
)
covariates = covariates.astype(np.float32)
# transform covariates (note: we fit the transformer on train split and can then transform the entire covariates series)
scaler_covs = Scaler()
cov_train, cov_val = covariates.split_after(training_cutoff)
scaler_covs.fit(cov_train)
covariates_transformed = scaler_covs.transform(covariates)
创建一个模型¶
如果你想生成确定性预测而不是分位数预测,你可以使用 PyTorch 损失函数(即设置 loss_fn=torch.nn.MSELoss() 和 likelihood=None)。
TFTModel 只有在给出某些未来输入时才能使用。可选参数 add_encoders 和 add_relative_index 可能非常有用,特别是当我们没有任何未来输入可用时。它们生成编码的时间数据,这些数据被用作未来协变量。
由于我们已经在示例中定义了未来协变量,因此它们被注释掉了。
[6]:
# default quantiles for QuantileRegression
quantiles = [
0.01,
0.05,
0.1,
0.15,
0.2,
0.25,
0.3,
0.4,
0.5,
0.6,
0.7,
0.75,
0.8,
0.85,
0.9,
0.95,
0.99,
]
input_chunk_length = 24
forecast_horizon = 12
my_model = TFTModel(
input_chunk_length=input_chunk_length,
output_chunk_length=forecast_horizon,
hidden_size=64,
lstm_layers=1,
num_attention_heads=4,
dropout=0.1,
batch_size=16,
n_epochs=300,
add_relative_index=False,
add_encoders=None,
likelihood=QuantileRegression(
quantiles=quantiles
), # QuantileRegression is set per default
# loss_fn=MSELoss(),
random_state=42,
)
训练 TFT¶
在接下来的内容中,我们可以直接将整个 covariates 系列作为 future_covariates 参数提供给模型;模型将切片这些协变量,并仅使用它需要的内容来训练以预测目标 train_transformed:
[7]:
my_model.fit(train_transformed, future_covariates=covariates_transformed, verbose=True)
[7]:
TFTModel(hidden_size=64, lstm_layers=1, num_attention_heads=4, full_attention=False, feed_forward=GatedResidualNetwork, dropout=0.1, hidden_continuous_size=8, categorical_embedding_sizes=None, add_relative_index=False, loss_fn=None, likelihood=<darts.utils.likelihood_models.QuantileRegression object at 0x7f92e0d64c70>, norm_type=LayerNorm, use_static_covariates=True, input_chunk_length=24, output_chunk_length=12, batch_size=16, n_epochs=300, add_encoders=None, random_state=42)
查看验证集上的预测¶
我们使用“当前”模型进行了一次24个月的预测——即,训练过程结束时的模型:
[8]:
def eval_model(model, n, actual_series, val_series):
pred_series = model.predict(n=n, num_samples=num_samples)
# plot actual series
plt.figure(figsize=figsize)
actual_series[: pred_series.end_time()].plot(label="actual")
# plot prediction with quantile ranges
pred_series.plot(
low_quantile=lowest_q, high_quantile=highest_q, label=label_q_outer
)
pred_series.plot(low_quantile=low_q, high_quantile=high_q, label=label_q_inner)
plt.title("MAPE: {:.2f}%".format(mape(val_series, pred_series)))
plt.legend()
eval_model(my_model, 24, series_transformed, val_transformed)
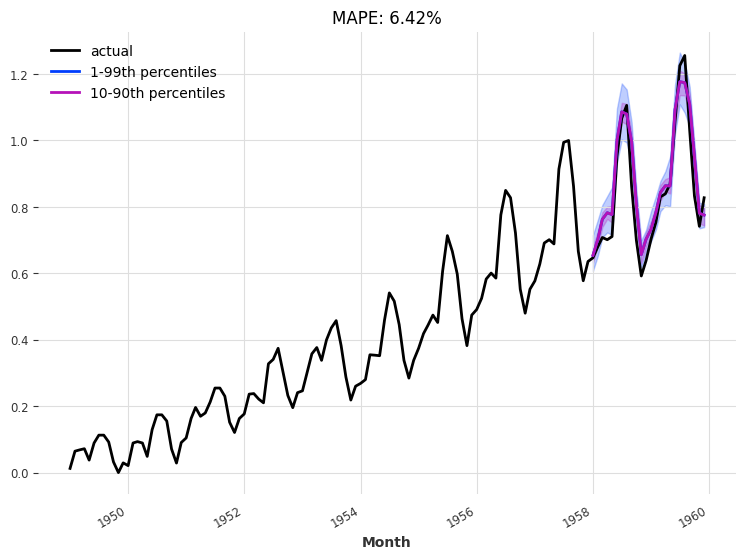
回测¶
让我们对 TFTModel 模型进行回测,看看它在过去3年内的12个月预测范围内表现如何:
[9]:
backtest_series = my_model.historical_forecasts(
series_transformed,
future_covariates=covariates_transformed,
start=train.end_time() + train.freq,
num_samples=num_samples,
forecast_horizon=forecast_horizon,
stride=forecast_horizon,
last_points_only=False,
retrain=False,
verbose=True,
)
[10]:
def eval_backtest(backtest_series, actual_series, horizon, start, transformer):
plt.figure(figsize=figsize)
actual_series.plot(label="actual")
backtest_series.plot(
low_quantile=lowest_q, high_quantile=highest_q, label=label_q_outer
)
backtest_series.plot(low_quantile=low_q, high_quantile=high_q, label=label_q_inner)
plt.legend()
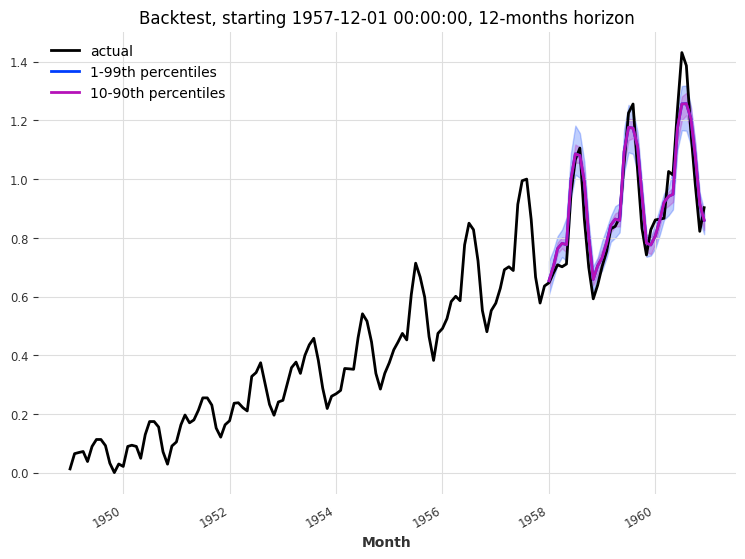
plt.title(f"Backtest, starting {start}, {horizon}-months horizon")
print(
"MAPE: {:.2f}%".format(
mape(
transformer.inverse_transform(actual_series),
transformer.inverse_transform(backtest_series),
)
)
)
eval_backtest(
backtest_series=concatenate(backtest_series),
actual_series=series_transformed,
horizon=forecast_horizon,
start=training_cutoff,
transformer=transformer,
)
MAPE: 4.90%
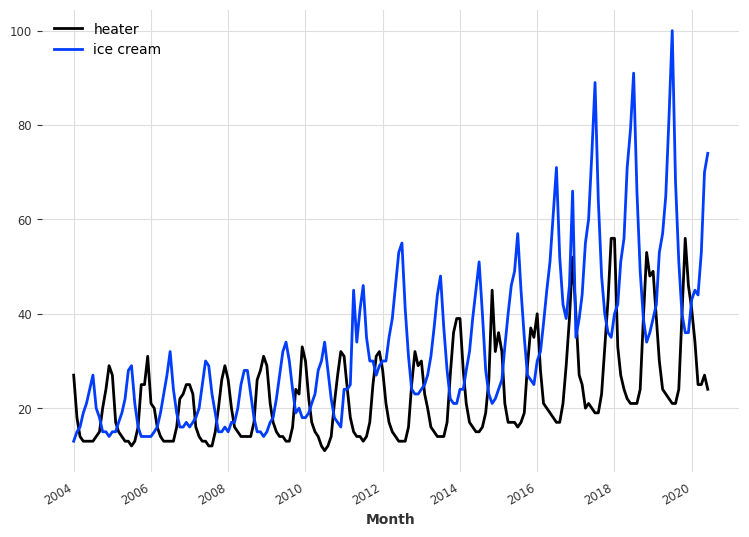
每月冰淇淋销售¶
让我们尝试另一个数据集。自2004年以来的每月冰淇淋和加热器销售数据。我们的目标是预测未来的冰淇淋销售。首先,我们从数据中构建时间序列,并检查其周期性。
[11]:
series_ice_heater = IceCreamHeaterDataset().load()
plt.figure(figsize=figsize)
series_ice_heater.plot()
print(check_seasonality(series_ice_heater["ice cream"], max_lag=36))
print(check_seasonality(series_ice_heater["heater"], max_lag=36))
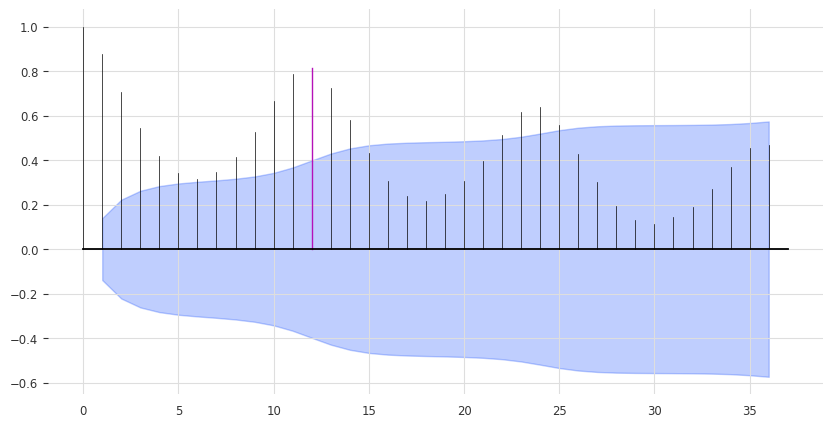
plt.figure(figsize=figsize)
plot_acf(series_ice_heater["ice cream"], 12, max_lag=36) # ~1 year seasonality
(True, 12)
(True, 12)
<Figure size 900x600 with 0 Axes>
处理数据¶
我们再次面临12个月的季节性。这次我们不会定义每月的未来协变量 -> 我们让模型自己处理这个问题!
让我们定义过去的协变量。如果我们使用过去的热水器销售数据来预测冰淇淋销售情况会怎样?
[12]:
# convert monthly sales to average daily sales per month
converted_series = []
for col in ["ice cream", "heater"]:
converted_series.append(
series_ice_heater[col]
/ TimeSeries.from_series(series_ice_heater.time_index.days_in_month)
)
converted_series = concatenate(converted_series, axis=1)
converted_series = converted_series[pd.Timestamp("20100101") :]
# define train/validation cutoff time
forecast_horizon_ice = 12
training_cutoff_ice = converted_series.time_index[-(2 * forecast_horizon_ice)]
# use ice cream sales as target, create train and validation sets and transform data
series_ice = converted_series["ice cream"]
train_ice, val_ice = series_ice.split_before(training_cutoff_ice)
transformer_ice = Scaler()
train_ice_transformed = transformer_ice.fit_transform(train_ice)
val_ice_transformed = transformer_ice.transform(val_ice)
series_ice_transformed = transformer_ice.transform(series_ice)
# use heater sales as past covariates and transform data
covariates_heat = converted_series["heater"]
cov_heat_train, cov_heat_val = covariates_heat.split_before(training_cutoff_ice)
transformer_heat = Scaler()
transformer_heat.fit(cov_heat_train)
covariates_heat_transformed = transformer_heat.transform(covariates_heat)
创建一个带有自动生成未来协变量的模型并进行训练¶
由于我们没有定义未来的协变量,我们需要告诉模型自行生成未来的协变量。
add_encoders: 可以从日期时间属性、循环重复的时间模式、索引位置和自定义函数中添加多种编码作为过去和/或未来的协变量。你甚至可以添加一个处理训练、验证和预测数据适当缩放的转换器!更多信息请参阅TFTModel文档 从这里add_relative_index: 为每个编码器-解码器块添加相对于预测点的缩放整数位置(如果你真的不想使用任何未来协变量,这可能很有用。位置值在所有块中保持不变,不会添加额外信息)。
我们使用 add_encoders={'cyclic': {'future': ['month']}} 来考虑作为未来协变量的12个月季节性。
[13]:
# use the last 3 years as past input data
input_chunk_length_ice = 36
# use `add_encoders` as we don't have future covariates
my_model_ice = TFTModel(
input_chunk_length=input_chunk_length_ice,
output_chunk_length=forecast_horizon_ice,
hidden_size=32,
lstm_layers=1,
batch_size=16,
n_epochs=300,
dropout=0.1,
add_encoders={"cyclic": {"future": ["month"]}},
add_relative_index=False,
optimizer_kwargs={"lr": 1e-3},
random_state=42,
)
# fit the model with past covariates
my_model_ice.fit(
train_ice_transformed, past_covariates=covariates_heat_transformed, verbose=True
)
[13]:
TFTModel(hidden_size=32, lstm_layers=1, num_attention_heads=4, full_attention=False, feed_forward=GatedResidualNetwork, dropout=0.1, hidden_continuous_size=8, categorical_embedding_sizes=None, add_relative_index=False, loss_fn=None, likelihood=None, norm_type=LayerNorm, use_static_covariates=True, input_chunk_length=36, output_chunk_length=12, batch_size=16, n_epochs=300, add_encoders={'cyclic': {'future': ['month']}}, optimizer_kwargs={'lr': 0.001}, random_state=42)
查看验证集上的预测¶
再次,我们使用“当前”模型进行24个月的单次预测——即,训练过程结束时的模型:
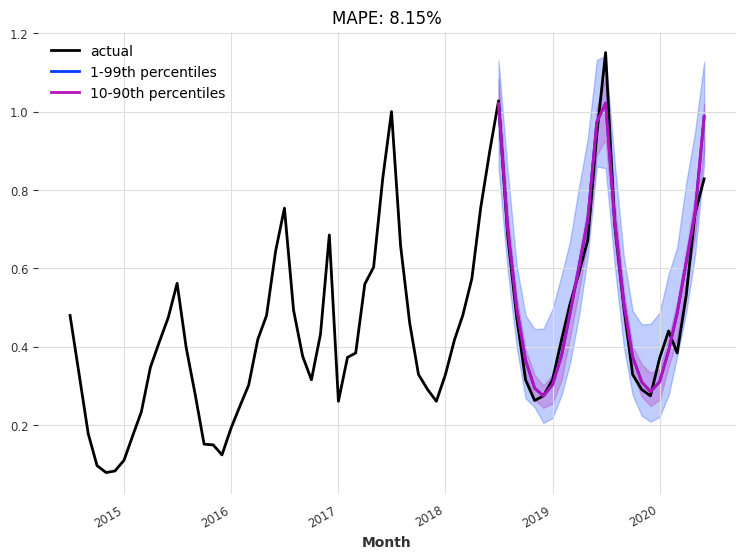
[14]:
n = 24
eval_model(
model=my_model_ice,
n=n,
actual_series=series_ice_transformed[
train_ice.end_time() - (2 * n - 1) * train_ice.freq :
],
val_series=val_ice_transformed,
)
回测¶
让我们对 TFTModel 模型进行回测,看看它在过去两年内以12个月的预测视野下的表现如何:
[15]:
# Compute the backtest predictions with the two models
last_points_only = False
backtest_series_ice = my_model_ice.historical_forecasts(
series_ice_transformed,
num_samples=num_samples,
start=training_cutoff_ice,
forecast_horizon=forecast_horizon_ice,
stride=1 if last_points_only else forecast_horizon_ice,
retrain=False,
last_points_only=last_points_only,
overlap_end=True,
verbose=True,
)
backtest_series_ice = (
concatenate(backtest_series_ice)
if isinstance(backtest_series_ice, list)
else backtest_series_ice
)
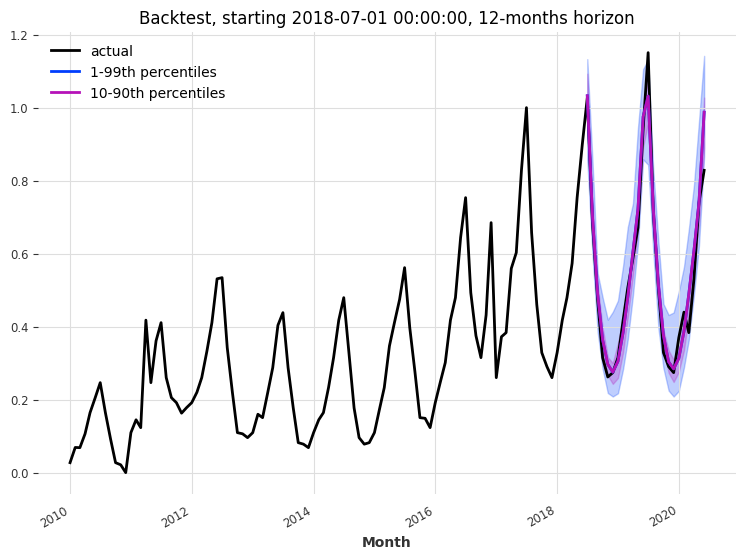
[16]:
eval_backtest(
backtest_series=backtest_series_ice,
actual_series=series_ice_transformed[
train_ice.start_time() - 2 * forecast_horizon_ice * train_ice.freq :
],
horizon=forecast_horizon_ice,
start=training_cutoff_ice,
transformer=transformer_ice,
)
MAPE: 5.32%
可解释性¶
让我们尝试理解我们的 TFTModel 模型学到了什么。如果能看到特征重要性以及模型如何关注过去和未来的输入,那就太好了。
TFTExplainer 正是这样做的!你可以在 这里 找到文档。
[17]:
from darts.explainability import TFTExplainer
要实例化解释器,我们有两个选项:- 传递一个自定义的背景序列输入,作为解释的默认输入。- 让解释器自动从模型中加载背景。这仅在模型是针对单一目标序列进行训练时才可能实现(如我们的情况)。
[18]:
explainer = TFTExplainer(my_model_ice)
现在我们可以使用 explain() 生成解释。对此我们又有两种选择:- 传递一个自定义的前景系列输入以进行解释 - 不传递任何前景以解释背景
[19]:
explainability_result = explainer.explain()
让我们看看特征重要性: - 编码器特征重要性:包含过去的目标、过去的协变量和“历史”未来协变量(输入块中未来协变量的值) - 解码器特征重要性:包含“未来”未来协变量(输出块中未来协变量的值) - 静态协变量重要性:静态变量的重要性(仅在模型使用带有静态协变量的``series``进行训练时显示)
[20]:
explainer.plot_variable_selection(explainability_result)
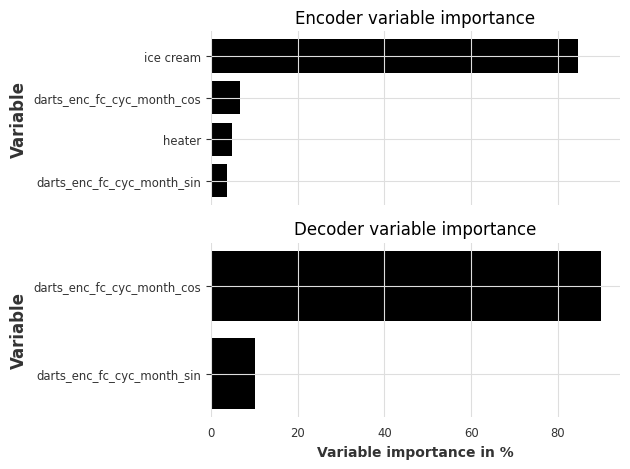
如预期,冰淇淋销售的历史记录是编码器中最重要的特征。月份的循环编码也有助于编码器和解码器学习季节性模式。
让我们看看模型对过去和未来输入的注意力(权重)。
我们有多种绘图选项:
plot_type - “time” - 绘制所有预测步骤的注意力聚合 - “all” - 分别绘制每个预测步骤的注意力(范围从 1 到 output_chunk_length) - “heatmap” - 将每个预测步骤的所有注意力绘制为热图
show_index_as - “relative” - 将 x 轴设置为相对于第一个预测时间步,范围从 -input_chunk_length 到 output_chunk_length - 1。 0 表示第一个预测时间步(用虚线标出)。 - “time” - 在 x 轴上使用实际的时间索引。虚线标出第一个预测时间步。
[21]:
explainer.plot_attention(explainability_result, plot_type="time")
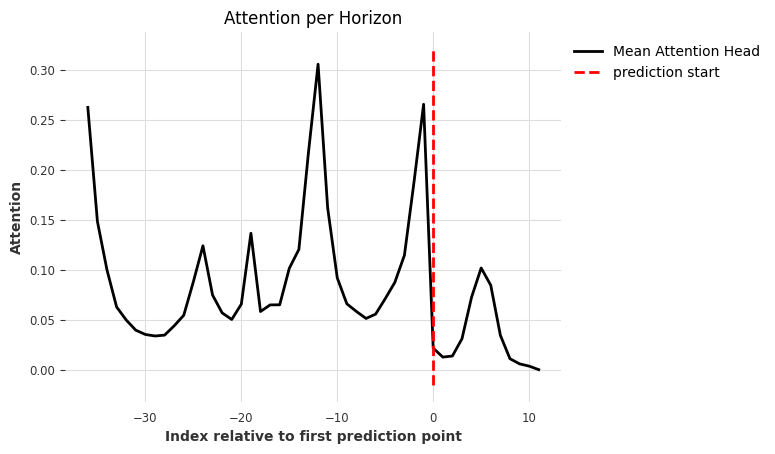
[21]:
<Axes: title={'center': 'Attention per Horizon'}, xlabel='Index relative to first prediction point', ylabel='Attention'>
我们可以看到有趣的关注区域: - 在相对索引 -12 处最大关注。这表明了年度季节性,对于冰淇淋销售来说是有意义的。 - 在输入块的开始处(-36)高度关注:这可能既来自于捕捉当前输入的值范围,也来自于季节性(-3 年) - 在输入块的末尾(-1)处更高的关注:模型关注于最近的过去 - 对未来输入的关注(我们将在下一张图中更详细地查看这一点)
[22]:
explainer.plot_attention(explainability_result, plot_type="all")
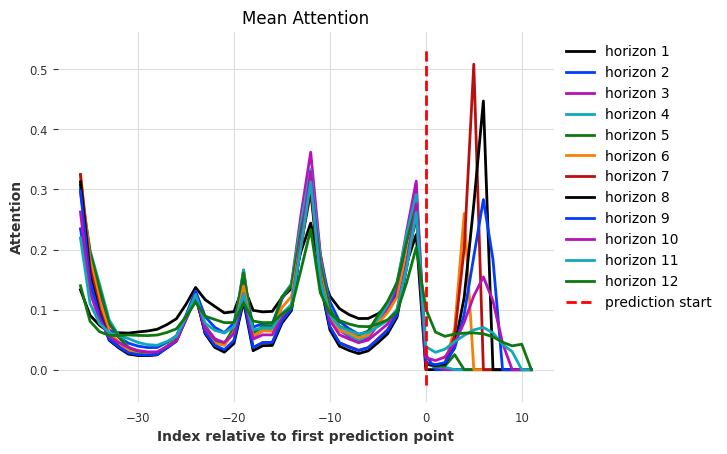
[22]:
<Axes: title={'center': 'Mean Attention'}, xlabel='Index relative to first prediction point', ylabel='Attention'>
在输出块(索引 0 - 11)中,我们看到模型仅关注每个时间范围的过去相对部分。这是因为 TFTModel 默认使用 full_attention=False。当将其设置为 True 时,模型还将关注当前和未来的输入。
[23]:
explainer.plot_attention(explainability_result, plot_type="heatmap")
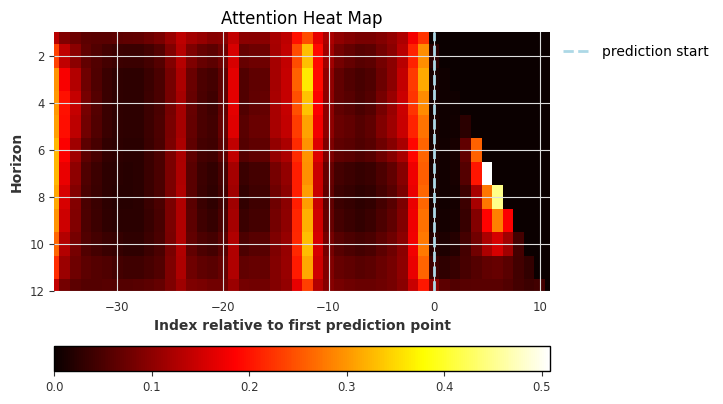
[23]:
<Axes: title={'center': 'Attention Heat Map'}, xlabel='Index relative to first prediction point', ylabel='Horizon'>
我们也可以直接从 exlainability_result 获取值。你可以在 这里 找到文档。
[24]:
explainability_result.get_encoder_importance()
[24]:
| darts_enc_fc_cyc_month_sin | heater | darts_enc_fc_cyc_month_cos | ice cream | |
|---|---|---|---|---|
| 0 | 3.7 | 4.8 | 6.8 | 84.7 |
[25]:
explainability_result.get_decoder_importance()
[25]:
| darts_enc_fc_cyc_month_sin | darts_enc_fc_cyc_month_cos | |
|---|---|---|
| 0 | 10.2 | 89.8 |
[26]:
explainability_result.get_static_covariates_importance()
[26]:
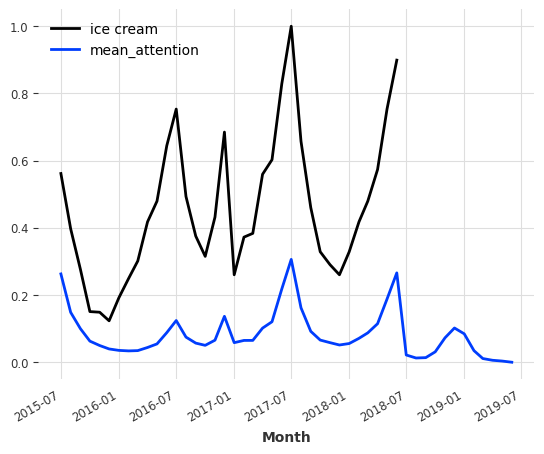
我们还可以将注意力提取为时间序列,并将其与数据进行绘制。
[27]:
attention = explainability_result.get_attention().mean(axis=1)
time_intersection = train_ice_transformed.time_index.intersection(attention.time_index)
train_ice_transformed[time_intersection].plot()
attention.plot(label="mean_attention", max_nr_components=12)
更多信息¶
尽管我们只看了一个单一的单变量预测示例,但 TFTExplainer 可以无缝应用于多变量和/或多个 TimeSeries 用例。