使用高斯过程滤波器进行过滤和预测¶
在这个笔记本中,我们将通过在噪声数据上拟合高斯过程来查看过滤噪声数据。
高斯过程滤波器,就像卡尔曼滤波器一样,是 Darts 中的一个 FilteringModel``(而不是 ``ForecastingModel)。FilteringModel 可以用于平滑序列,或者尝试从被噪声污染的数据中推断出“真实”数据。
在处理高斯过程的情况下,这是通过对真实数据点所在的基础函数的形状做出假设来完成的。这些假设(例如平滑性、周期性等)被编码在核函数中。
在这个笔记本中,我们将生成一个简单的周期信号,并看看如何使用高斯过程滤波器来去噪。
[ ]:
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.gaussian_process.kernels import ExpSineSquared, RBF
from darts import TimeSeries
from darts.models import GaussianProcessFilter
from darts.utils import timeseries_generation as tg
向正弦波添加白噪声¶
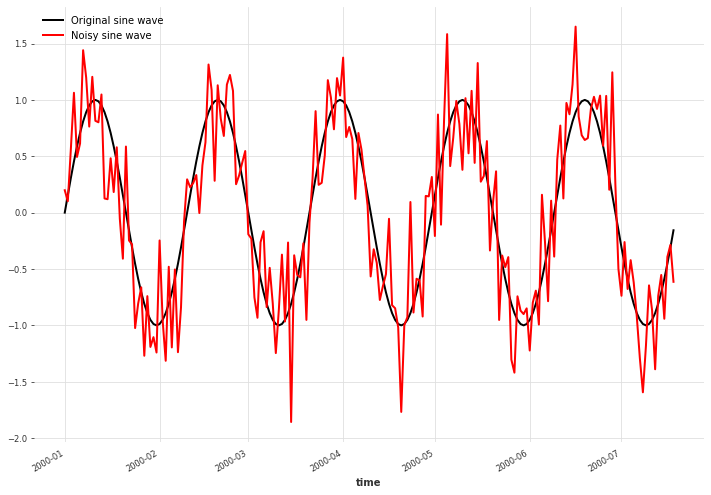
我们创建一个简单的正弦波信号,并为其添加高斯噪声。
[2]:
NOISE_DISTANCE = 0.4
SAMPLE_SIZE = 200
np.random.seed(42)
# Prepare the sine wave
x = tg.sine_timeseries(length=SAMPLE_SIZE, value_frequency=0.025)
# Add white noise
noise = tg.gaussian_timeseries(length=SAMPLE_SIZE, std=NOISE_DISTANCE)
x_noise = x + noise
plt.figure(figsize=[12, 8])
x.plot(label="Original sine wave")
x_noise.plot(color="red", label="Noisy sine wave")
plt.legend()
plt.show()
使用周期核推断高斯过程的均值¶
接下来,我们使用 ExpSineSquared 核在数据上拟合一个高斯过程。这个核编码了一个周期性假设,这适用于我们的数据。你可以尝试取消注释 kernel = RBF() 这一行,将核更改为 RBF 核,它只施加了函数的平滑性。更多关于(高斯过程)核及其组合方式的信息,请参见 The Kernel Cookbook。
GaussianProcessFilter 构造函数接受与 scikit-learn 的 GaussianProcessRegressor 相同的参数,后者是其依赖的对象。scikit-learn 中实现的核函数可以在 这里 找到。
在这里,我们设置了一个相对噪声方差 alpha=0.2 ,因为我们确切地知道之前添加了多少噪声,但在实际应用中这将需要估计。
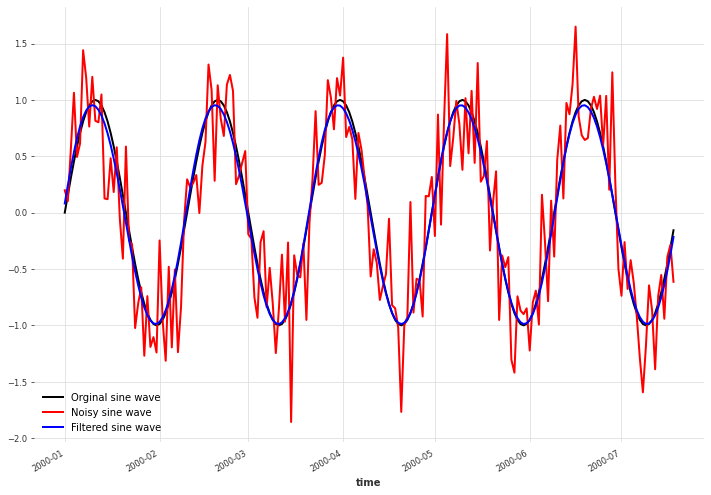
我们看到高斯过程的均值非常接近原始信号。不过请记住,真实数据很少会如此完美地周期性,因此需要更多地试验核函数和噪声水平。
[3]:
kernel = ExpSineSquared()
# kernel = RBF()
gpf = GaussianProcessFilter(
kernel=kernel, alpha=NOISE_DISTANCE / 2, n_restarts_optimizer=100
)
filtered_x = gpf.filter(x_noise)
plt.figure(figsize=[12, 8])
x.plot(color="black", label="Orginal sine wave")
x_noise.plot(color="red", label="Noisy sine wave")
filtered_x.plot(color="blue", label="Filtered sine wave")
plt.legend()
[3]:
<matplotlib.legend.Legend at 0x166c993a0>
高斯过程的样本¶
高斯过程是一个概率模型,这意味着模型的预测是分布而不是单一值。
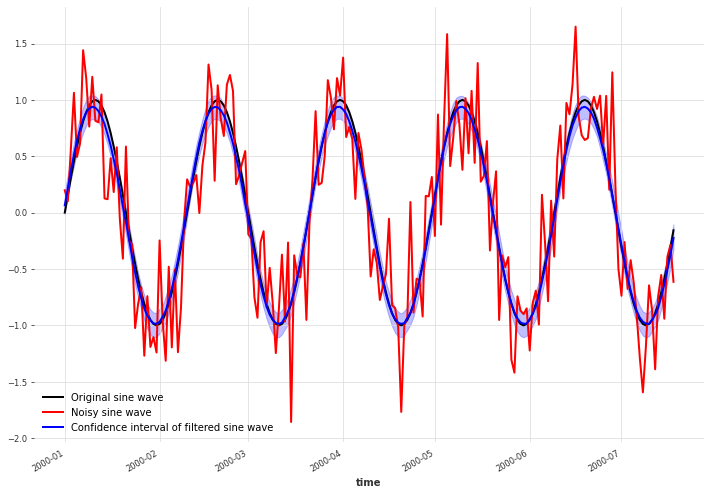
之前,我们只是使用了这些分布在感兴趣点的均值来绘制曲线。这里,我们将从分布中采样并绘制90%置信区间。由此我们可以看到,关于基础数据的不确定性在波峰和波谷处比其他地方更大。
[5]:
filtered_x_samples = gpf.filter(x_noise, num_samples=100)
plt.figure(figsize=[12, 8])
x.plot(color="black", label="Original sine wave")
x_noise.plot(color="red", label="Noisy sine wave")
filtered_x_samples.plot(color="blue", label="Confidence interval of filtered sine wave")
plt.legend()
[5]:
<matplotlib.legend.Legend at 0x166b2eca0>
带有缺失数据点的正态过程样本¶
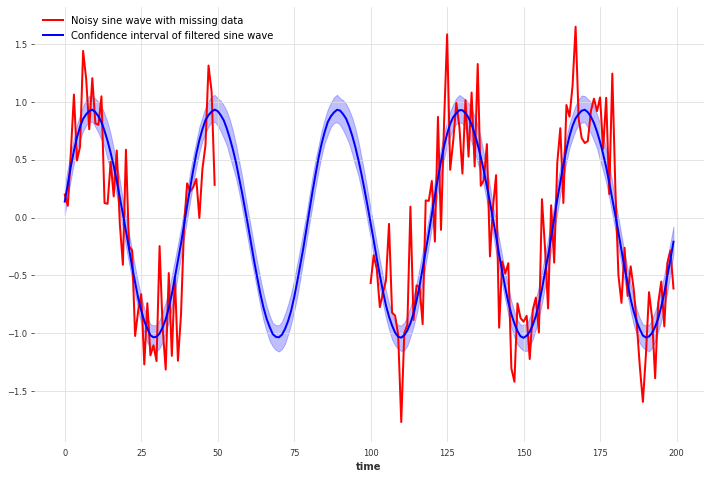
我们甚至可以在包含缺失(NaN)数据点的时间序列上使用高斯过程滤波器。
对于我们的周期信号,高斯过程使用周期核很好地估计了缺失数据。你可以看到当使用RBF核时,这种变化以及不确定性是如何增加的。
[7]:
x_missing_arr = x_noise.values()
x_missing_arr[50:100] = np.nan
x_missing = TimeSeries.from_values(x_missing_arr)
kernel = ExpSineSquared()
# kernel = RBF()
gpf_missing = GaussianProcessFilter(kernel=kernel, alpha=0.2, n_restarts_optimizer=100)
filtered_x_missing_samples = gpf_missing.filter(x_missing, num_samples=100)
plt.figure(figsize=[12, 8])
x_missing.plot(color="red", label="Noisy sine wave with missing data")
filtered_x_missing_samples.plot(
color="blue", label="Confidence interval of filtered sine wave"
)
plt.legend()
[7]:
<matplotlib.legend.Legend at 0x166db4a00>
[ ]: