ARIMA 模型


# 此单元格不会被渲染，但用于隐藏警告。

import warnings
warnings.filterwarnings("ignore")

import logging
logging.getLogger('statsforecast').setLevel(logging.ERROR)

import pandas as pd
pd.set_option('display.max_rows', 6)

使用 Statsforecast 的 ARIMA 模型 的逐步指南。

在本指南中，我们将熟悉主要的 StatsForecast 类及一些相关方法，例如 StatsForecast.plot、StatsForecast.forecast 和 StatsForecast.cross_validation。

介绍
ARIMA模型
ARIMA模型中p、d和q的意义
自回归和移动平均模型
ARIMA模型
如何确定ARIMA模型中的差分阶数(d)
加载库和数据
使用绘图方法探索数据
如何确定自回归项的阶数(p)
如何确定移动平均项的阶数(q)
如何处理时间序列稍微欠差或过差的情况
使用StatsForecast实现ARIMA
交叉验证
模型评估
参考文献

介绍

时间序列 是指在不同时间间隔记录的一系列数据点。时间顺序可以是按日、按月，甚至按年。
时间序列预测是利用统计模型根据过去的结果预测时间序列未来值的过程。
在之前的笔记本中，我们讨论了 时间序列预测 的各个方面。
预测是我们想要预测序列将来将要采取的值的步骤。时间序列的预测通常具有巨大的商业价值。

时间序列的预测可大致分为两种类型。

如果我们仅使用时间序列的先前值来预测其未来值，这被称为 单变量时间序列预测。
如果我们使用除该序列之外的其他预测变量（如外生变量）来进行预测，这被称为 多变量时间序列预测。
本笔记本专注于一种特定类型的预测方法，即 ARIMA 建模。

ARIMA模型简介

ARIMA代表自回归积分滑动平均模型。它属于一种模型类别，该类别根据给定时间序列的过去值（即它自己的滞后值和滞后的预测误差）来解释该时间序列。该方程可用于预测未来值。任何表现出模式且不是随机白噪声的“非季节性”时间序列都可以使用ARIMA模型进行建模。
因此，ARIMA，即自回归积分滑动平均的简称，是一种基于过去时间序列值的信息可以单独用于预测未来值的思想的预测算法。
ARIMA模型由三个顺序参数指定：(p, d, q)，

其中，
- p是AR项的阶数
- q是MA项的阶数
- d是使时间序列平稳所需的差分次数
AR(p)自回归 - 一种回归模型，利用当前观测值与先前时间段的观测值之间的依赖关系。自回归(AR(p))成分指在时间序列的回归方程中使用过去值。
I(d)积分 - 通过对观测值进行差分（从当前观测值中减去先前时间步的观测值）来使时间序列平稳。差分涉及将序列的当前值与其之前值相减d次。
MA(q)移动平均 - 一种模型，使用观测值与应用于滞后观测值的移动平均模型的残差错误之间的依赖关系。移动平均成分将模型的误差表示为先前误差项的组合。阶数q表示要包含在模型中的项数。

ARIMA模型的类型

ARIMA : 非季节性自回归积分滑动平均
SARIMA : 季节性ARIMA
SARIMAX : 带外生变量的季节性ARIMA

如果一个时间序列具有季节性模式，那么我们需要添加季节性项，变成SARIMA，即季节性ARIMA。

ARIMA模型中p、d和q的含义

p的含义

p是自回归（AR）项的阶数。它指的是用于作为预测变量的Y的滞后数量。

d的含义

在ARIMA中，自回归这个术语意味着它是一个线性回归模型，使用自身的滞后作为预测变量。我们知道，线性回归模型在预测变量不相关且彼此独立时效果最佳。因此，我们需要使时间序列平稳。
使序列平稳的最常见方法是进行差分。也就是说，从当前值中减去前一个值。有时，根据序列的复杂性，可能需要进行多次差分。
因此，d的值是使序列平稳所需的最小差分次数。如果时间序列已经是平稳的，则d = 0。

q的含义

q是移动平均（MA）项的阶数。它指的是应包含在ARIMA模型中的滞后预测误差的数量。

自回归和移动平均模型

自回归模型

在自回归模型中，我们使用变量过去值的线性组合来预测感兴趣的变量。自回归一词表明这是对变量自身的回归。

因此，一个阶数为 p 的自回归模型可以写为：

\[ \begin{equation} y_{t} = c + \phi_{1}y_{t-1} + \phi_{2}y_{t-2} + \dots + \phi_{p}y_{t-p} + \varepsilon_{t} \tag{1} \end{equation} \]

其中 $\varepsilon_t$ 是白噪声。这类似于多元回归，但用滞后值 $y_t$ 作为预测变量。我们将其称为 AR(p) 模型，即阶数为 p 的自回归模型。

移动平均模型

移动平均模型不是使用预测变量的过去值进行回归，而是在类似回归的模型中使用过去的预测误差：

\[ \begin{equation} y_{t} = c + \varepsilon_t + \theta_{1}\varepsilon_{t-1} + \theta_{2}\varepsilon_{t-2} + \dots + \theta_{q}\varepsilon_{t-q} \tag{2} \end{equation} \]

其中 $\varepsilon_t$ 是白噪声。我们将其称为 MA(q) 模型，即阶数为 q 的移动平均模型。显然，我们无法观察到 $\varepsilon_t$ 的值，因此这并不是真正意义上的回归。

请注意，$y_t$ 的每个值可以被视为过去几次预测误差的加权移动平均（尽管系数通常不会加起来为一）。然而，移动平均模型不应与移动平均平滑混淆。移动平均模型用于预测未来值，而移动平均平滑用于估计过去值的趋势周期。

因此，我们分别讨论了自回归和移动平均模型。

ARIMA模型

如果我们将差分与自回归和移动平均模型结合起来，就得到了一个非季节性ARIMA模型。ARIMA是自回归积分移动平均的缩写（在这个上下文中，“积分”是差分的反过程）。完整模型可以写为

\[\begin{equation} y'_{t} = c + \phi_{1}y'_{t-1} + \cdots + \phi_{p}y'_{t-p} + \theta_{1}\varepsilon_{t-1} + \cdots + \theta_{q}\varepsilon_{t-q} + \varepsilon_{t}, \tag{3} \end{equation}\]

其中 $y'_{t}$ 是差分后的序列（它可能经过多次差分）。右侧的“预测变量”包括 $y_t$ 的滞后值和滞后误差。我们称之为ARIMA(p,d,q)模型，其中

p	自回归部分的阶数
d	涉及的一阶差分的程度
q	移动平均部分的阶数

与自回归和移动平均模型相同的平稳性和可逆性条件也适用于ARIMA模型。

我们已经讨论的许多模型是ARIMA模型的特例，如下表所示：

模型	p d q	差分形式	方法
Arima(0,0,0)	0 0 0	$y_t=Y_t$	白噪声
ARIMA (0,1,0)	0 1 0	$y_t = Y_t - Y_{t-1}$	随机游走
ARIMA (0,2,0)	0 2 0	$y_t = Y_t - 2Y_{t-1} + Y_{t-2}$	常数
ARIMA (1,0,0)	1 0 0	$\hat Y_t = \mu + \Phi_1 Y_{t-1} + \epsilon$	AR(1)：一阶回归模型
ARIMA (2, 0, 0)	2 0 0	$\hat Y_t = \Phi_0 + \Phi_1 Y_{t-1} + \Phi_2 Y_{t-2} + \epsilon$	AR(2)：二阶回归模型
ARIMA (1, 1, 0)	1 1 0	$\hat Y_t = \mu + Y_{t-1} + \Phi_1 (Y_{t-1}- Y_{t-2})$	差分一阶自回归模型
ARIMA (0, 1, 1)	0 1 1	$\hat Y_t = Y_{t-1} - \Phi_1 e^{t-1}$	简单指数平滑
ARIMA (0, 0, 1)	0 0 1	$\hat Y_t = \mu_0+ \epsilon_t - \omega_1 \epsilon_{t-1}$	MA(1)：一阶回归模型
ARIMA (0, 0, 2)	0 0 2	$\hat Y_t = \mu_0+ \epsilon_t - \omega_1 \epsilon_{t-1} - \omega_2 \epsilon_{t-2}$	MA(2)：二阶回归模型
ARIMA (1, 0, 1)	1 0 1	$\hat Y_t = \Phi_0 + \Phi_1 Y_{t-1}+ \epsilon_t - \omega_1 \epsilon_{t-1}$	ARMA模型
ARIMA (1, 1, 1)	1 1 1	$\Delta Y_t = \Phi_1 Y_{t-1} + \epsilon_t - \omega_1 \epsilon_{t-1}$	ARIMA模型
ARIMA (1, 1, 2)	1 1 2	$\hat Y_t = Y_{t-1} + \Phi_1 (Y_{t-1} - Y_{t-2} )- \Theta_1 e_{t-1} - \Theta_1 e_{t-1}$	阶梯趋势线性指数平滑
ARIMA (0, 2, 1) 或 (0,2,2)	0 2 1	$\hat Y_t = 2 Y_{t-1} - Y_{t-2} - \Theta_1 e_{t-1} - \Theta_2 e_{t-2}$	线性指数平滑

一旦我们开始以这种方式组合组件以形成更复杂的模型，使用反移位符号工作会容易得多。例如，上述方程可以用反移位符号写为

\[\begin{equation} \tag{4} \begin{array}{c c c c} (1-\phi_1B - \cdots - \phi_p B^p) & (1-B)^d y_{t} &= &c + (1 + \theta_1 B + \cdots + \theta_q B^q)\varepsilon_t\\ {\uparrow} & {\uparrow} & &{\uparrow}\\ \text{AR($p$)} & \text{$d$次差分} & & \text{MA($q$)}\\ \end{array} \end{equation}\]

用语言描述ARIMA模型

预测的 Yt = 常数 + Y 的线性组合滞后（最多 p 个滞后） + 滞后预测误差的线性组合（最多 q 个滞后）

如何在ARIMA模型中找到差分阶数(d)

如前所述，差分的目的是使时间序列平稳。但是我们应该小心，不要过度差分这个序列。过度差分的序列可能仍然是平稳的，这反过来会影响模型参数。
因此，我们应该确定正确的差分阶数。正确的差分阶数是获取一个近乎平稳的序列所需的最小差分，该序列围绕一个定义的均值波动，并且自相关函数(ACF)图很快就会降至零。
如果自相关在许多滞后期（10个或更多）中是正数，则该序列需要进一步差分。另一方面，如果滞后1的自相关本身过于负，则该序列可能已经过度差分。
如果我们在两种差分阶数之间无法真正决定，那么我们选择那种在差分序列中标准差最小的阶数。
现在，我们将通过以下示例来解释这些概念：
- 首先，我将使用增强型迪基-福勒检验（ADF检验）来检查序列是否平稳，该检验来自statsmodels包。原因在于，只有在序列非平稳时，我们才需要差分。否则，就不需要差分，也就是说d=0。
- ADF检验的原假设（Ho）是时间序列是非平稳的。因此，如果检验的p值小于显著性水平（0.05），我们就拒绝原假设，并推断时间序列确实是平稳的。
- 所以，在我们的例子中，如果P值 > 0.05，我们将继续寻找差分的阶数。

加载库和数据

Tip

需要使用Statsforecast。有关安装说明，请参见说明。

接下来，我们导入绘图库并配置绘图样式。

import matplotlib.pyplot as plt

plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
dark_style = {
    'figure.facecolor': '#212946',
    'axes.facecolor': '#212946',
    'savefig.facecolor':'#212946',
    'axes.grid': True,
    'axes.grid.which': 'both',
    'axes.spines.left': False,
    'axes.spines.right': False,
    'axes.spines.top': False,
    'axes.spines.bottom': False,
    'grid.color': '#2A3459',
    'grid.linewidth': '1',
    'text.color': '0.9',
    'axes.labelcolor': '0.9',
    'xtick.color': '0.9',
    'ytick.color': '0.9',
    'font.size': 12 }
plt.rcParams.update(dark_style)

from pylab import rcParams
rcParams['figure.figsize'] = (18,7)

读取数据

import pandas as pd
import numpy as np

df = pd.read_csv("https://raw.githubusercontent.com/Naren8520/Serie-de-tiempo-con-Machine-Learning/main/Data/Esperanza_vida.csv", usecols=[1,2])
df.head()

	year	value
0	1960-01-01	69.123902
1	1961-01-01	69.760244
2	1962-01-01	69.149756
3	1963-01-01	69.248049
4	1964-01-01	70.311707

StatsForecast 的输入始终是一个长格式的数据框，包含三列：unique_id、ds 和 y：

unique_id（字符串、整数或类别）表示系列的标识符。
ds（日期戳）列应为 Pandas 期望的格式，理想情况下为 YYYY-MM-DD 的日期格式或 YYYY-MM-DD HH:MM:SS 的时间戳格式。
y（数值型）表示我们希望进行预测的测量值。

df["unique_id"]="1"
df.columns=["ds", "y", "unique_id"]
df.head()

	ds	y	unique_id
0	1960-01-01	69.123902	1
1	1961-01-01	69.760244	1
2	1962-01-01	69.149756	1
3	1963-01-01	69.248049	1
4	1964-01-01	70.311707	1

print(df.dtypes)

ds            object
y            float64
unique_id     object
dtype: object

我们需要将ds从object类型转换为日期时间。

df["ds"] = pd.to_datetime(df["ds"])

使用plot方法探索数据

使用StatsForecast类中的plot方法绘制一个序列。此方法从数据集中打印一个随机序列，对于基础的探索性数据分析（EDA）非常有用。

from statsforecast import StatsForecast

StatsForecast.plot(df)

通过观察图表，我们可以看到在这段时间内存在一个上升的趋势。

df["y"].plot(kind='kde',figsize = (16,5))
df["y"].describe()

count    60.000000
mean     76.632439
std       4.495279
           ...    
50%      76.895122
75%      80.781098
max      83.346341
Name: y, Length: 8, dtype: float64

季节分解

如何分解时间序列以及为什么要这样做？

在时间序列分析中，为了预测新值，了解过去的数据非常重要。更正式地说，了解随时间变化的值的模式是非常重要的。导致我们预测值出现错误方向的原因可能有很多。基本上，时间序列由四个组件组成。这些组件的变化导致时间序列模式的变化。这些组件是：

水平（Level）： 这是在一段时间内的主要平均值。
趋势（Trend）： 趋势是导致时间序列中模式增加或减少的值。
季节性（Seasonality）： 这是在时间序列中短期内发生的周期性事件，导致时间序列中短期的增加或减少模式。
残差/噪音（Residual/Noise）： 这些是时间序列中的随机变化。

这些组件随时间的组合导致时间序列的形成。大多数时间序列由水平和噪音/残差组成，趋势或季节性是可选值。

如果季节性和趋势是时间序列的一部分，那么将会影响预测值。因为预测时间序列的模式可能与之前的时间序列不同。

时间序列中组件的组合可以分为两种类型： * 加法（Additive） * 乘法（Multiplicative）

加法时间序列

如果时间序列的组件通过相加来构成时间序列，则该时间序列称为加法时间序列。通过可视化，我们可以说，如果时间序列的增加或减少模式在整个序列中是相似的，则该时间序列是加法的。任何加法时间序列的数学函数可以表示为： \[y(t) = 水平 + 趋势 + 季节性 + 噪音\]

乘法时间序列

如果时间序列的组件是相乘在一起的，则该时间序列称为乘法时间序列。从可视化来看，如果该时间序列随着时间的推移呈现指数增长或下降，则该时间序列可以视为乘法时间序列。乘法时间序列的数学函数可以表示为： \[y(t) = 水平 * 趋势 * 季节性 * 噪音\]

from statsmodels.tsa.seasonal import seasonal_decompose

decomposed=seasonal_decompose(df["y"], model = "add", period=1)
decomposed.plot()
plt.show()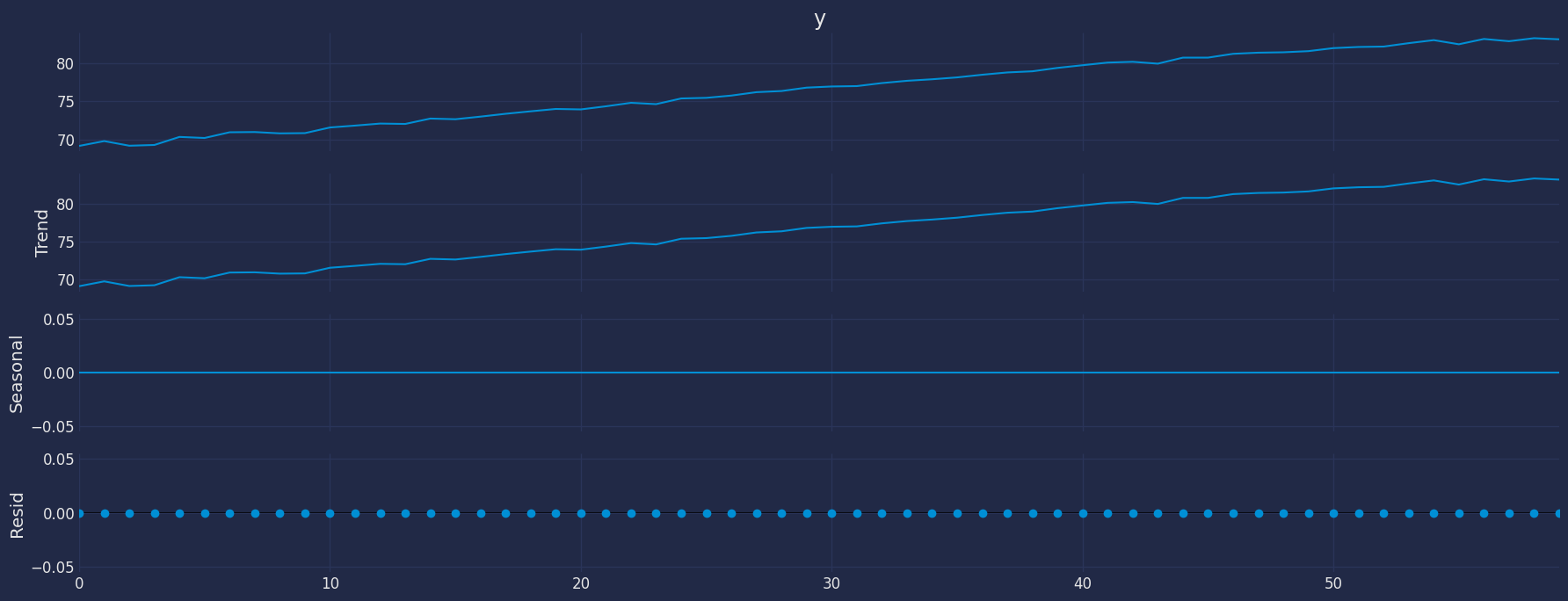

增强型迪基-福勒检验

增强型迪基-福勒（ADF）检验是一种统计检验，旨在确定时间序列数据中是否存在单位根。单位根可能会导致时间序列分析结果的不确定性。在单位根检验中形成一个原假设，以确定时间序列数据受到趋势影响的强度。接受原假设意味着我们接受时间序列数据不是平稳的证据。拒绝原假设或接受替代假设意味着我们接受时间序列数据是由一个平稳过程生成的证据。这个过程也被称为平稳趋势。ADF检验统计量的值是负的。较低的ADF值表示对原假设的拒绝程度更强。

增强型迪基-福勒检验是一种常用的统计检验，用于测试给定的时间序列是否是平稳的。我们可以通过定义原假设和替代假设来实现这一点。

原假设：时间序列是非平稳的。它给出一个时间相关的趋势。替代假设：时间序列是平稳的。换句话说，序列不依赖于时间。

ADF或t统计量 < 临界值：拒绝原假设，时间序列是平稳的。 ADF或t统计量 > 临界值：未能拒绝原假设，时间序列是非平稳的。

from statsmodels.tsa.stattools import adfuller

def Augmented_Dickey_Fuller_Test_func(series , column_name):
    print (f'Dickey-Fuller test results for columns: {column_name}')
    dftest = adfuller(series, autolag='AIC')
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','No Lags Used','Number of observations used'])
    for key,value in dftest[4].items():
        dfoutput['Critical Value (%s)'%key] = value
    print (dfoutput)
    if dftest[1] <= 0.05:
        print("Conclusion:====>")
        print("Reject the null hypothesis")
        print("The data is stationary")
    else:
        print("Conclusion:====>")
        print("The null hypothesis cannot be rejected")
        print("The data is not stationary")

Augmented_Dickey_Fuller_Test_func(df["y"],"Life expectancy")

Dickey-Fuller test results for columns: Life expectancy
Test Statistic         -1.578590
p-value                 0.494339
No Lags Used            2.000000
                          ...   
Critical Value (1%)    -3.550670
Critical Value (5%)    -2.913766
Critical Value (10%)   -2.594624
Length: 7, dtype: float64
Conclusion:====>
The null hypothesis cannot be rejected
The data is not stationary

我们可以在结果中看到，我们获得了非平稳序列，因为p值大于5%。

应用ADF检验的一个目的就是了解我们的序列是否是平稳的。根据ADF检验的结果，我们可以确定下一步。在我们的案例中，从之前的结果可以看出，时间序列是非平稳的，因此我们将进行下一步，即对我们的时间序列进行差分。

我们将创建一个数据的副本，目的是调查以寻找我们时间序列的平稳性。

一旦我们制作了时间序列的副本，我们将对其进行差分，然后使用扩展的迪基-福勒检验来调查我们的时间序列是否是平稳的。

df1=df.copy()
df1['y_diff'] = df['y'].diff()
df1.dropna(inplace=True)
df1.head()

	ds	y	unique_id	y_diff
1	1961-01-01	69.760244	1	0.636341
2	1962-01-01	69.149756	1	-0.610488
3	1963-01-01	69.248049	1	0.098293
4	1964-01-01	70.311707	1	1.063659
5	1965-01-01	70.171707	1	-0.140000

让我们再次应用迪基-福勒检验，以找出我们的时间序列是否已经平稳。

Augmented_Dickey_Fuller_Test_func(df1["y_diff"],"Life expectancy")

Dickey-Fuller test results for columns: Life expectancy
Test Statistic         -8.510100e+00
p-value                 1.173776e-13
No Lags Used            1.000000e+00
                            ...     
Critical Value (1%)    -3.550670e+00
Critical Value (5%)    -2.913766e+00
Critical Value (10%)   -2.594624e+00
Length: 7, dtype: float64
Conclusion:====>
Reject the null hypothesis
The data is stationary

我们可以在之前的结果中观察到，如果我们的时间序列是平稳的，则 p 值小于 5%。

现在我们的时间序列是平稳的，也就是说，我们只进行了 1 次差分，因此，我们的参数 $d=1$。

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt


fig, axes = plt.subplots(2, 2, )
axes[0, 0].plot(df1["y"]); axes[0, 0].set_title('Original Series')
plot_acf(df1["y"], ax=axes[0, 1],lags=20)

axes[1, 0].plot(df1["y"].diff()); axes[1, 0].set_title('1st Order Differencing')
plot_acf(df1["y"].diff().dropna(), ax=axes[1, 1],lags=20)


plt.show()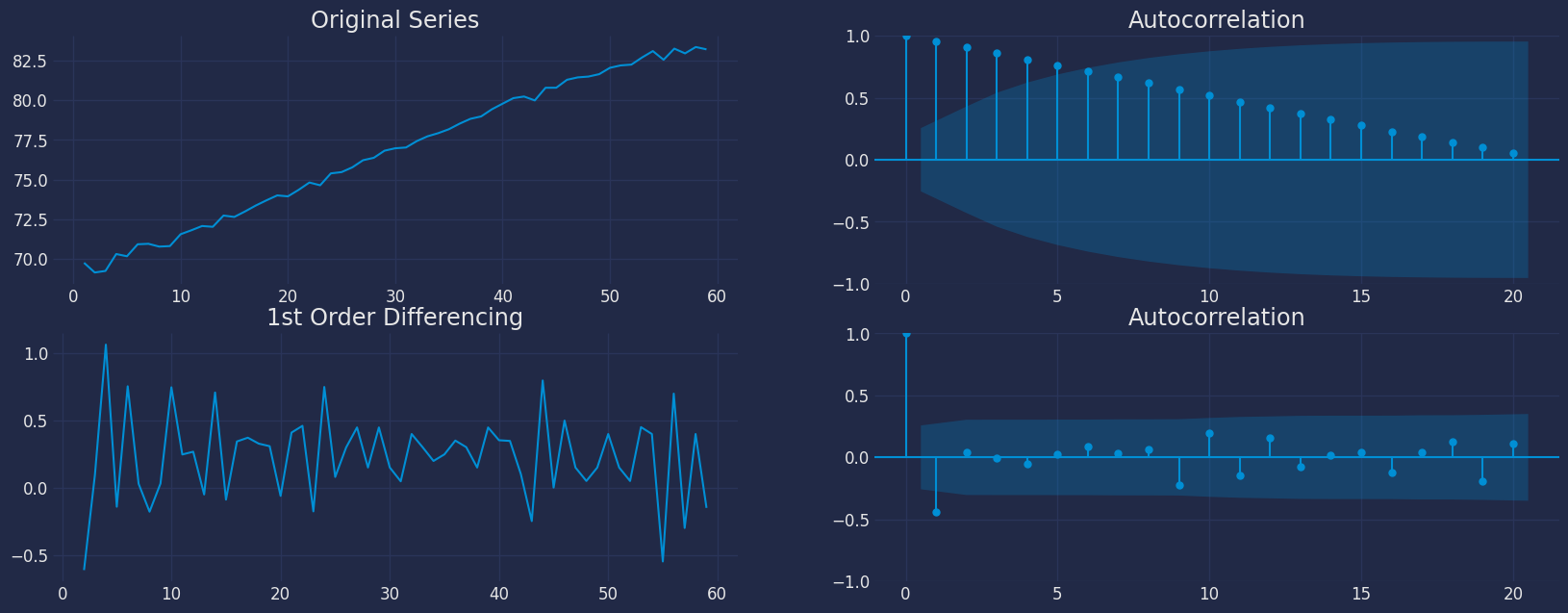

对于上述数据，我们可以看到时间序列在进行一阶差分后达到了平稳性。

如何找到AR项的阶数 (p)

下一步是确定模型是否需要任何AR项。我们将通过检查部分自相关(PACF)图来找出所需的AR项数量。
部分自相关可以理解为序列与其滞后之间的相关性，在此过程中排除了中间滞后的影响。因此，PACF在某种程度上传达了滞后与序列之间的纯相关性。通过这种方式，我们将知道该滞后是否需要在AR项中。
序列滞后(k)的部分自相关是$Y$的自回归方程中该滞后的系数。

\[Y_t = \alpha_0 + \alpha_1 Y_{t-1} + \alpha_2 Y_{t-2} + \alpha_3 Y_{t-3}\]

也就是说，假设$Y_t$是当前序列，而$Y_{t-1}$是$Y$的滞后1，那么滞后3$(Y_{t-3})$的部分自相关就是上述方程中$Y_{t-3}$的系数$\alpha_3$。
现在，我们应该找出AR项的数量。任何在平稳化序列中的自相关都可以通过添加足够的AR项来纠正。因此，我们最初将AR项的阶数设为在PACF图中超过显著性限制的滞后的数量。

fig, axes = plt.subplots(1, 2)
axes[0].plot(df1["y"].diff()); axes[0].set_title('1st Differencing')
axes[1].set(ylim=(0,5))
plot_pacf(df1["y"].diff().dropna(), ax=axes[1],lags=20)

plt.show()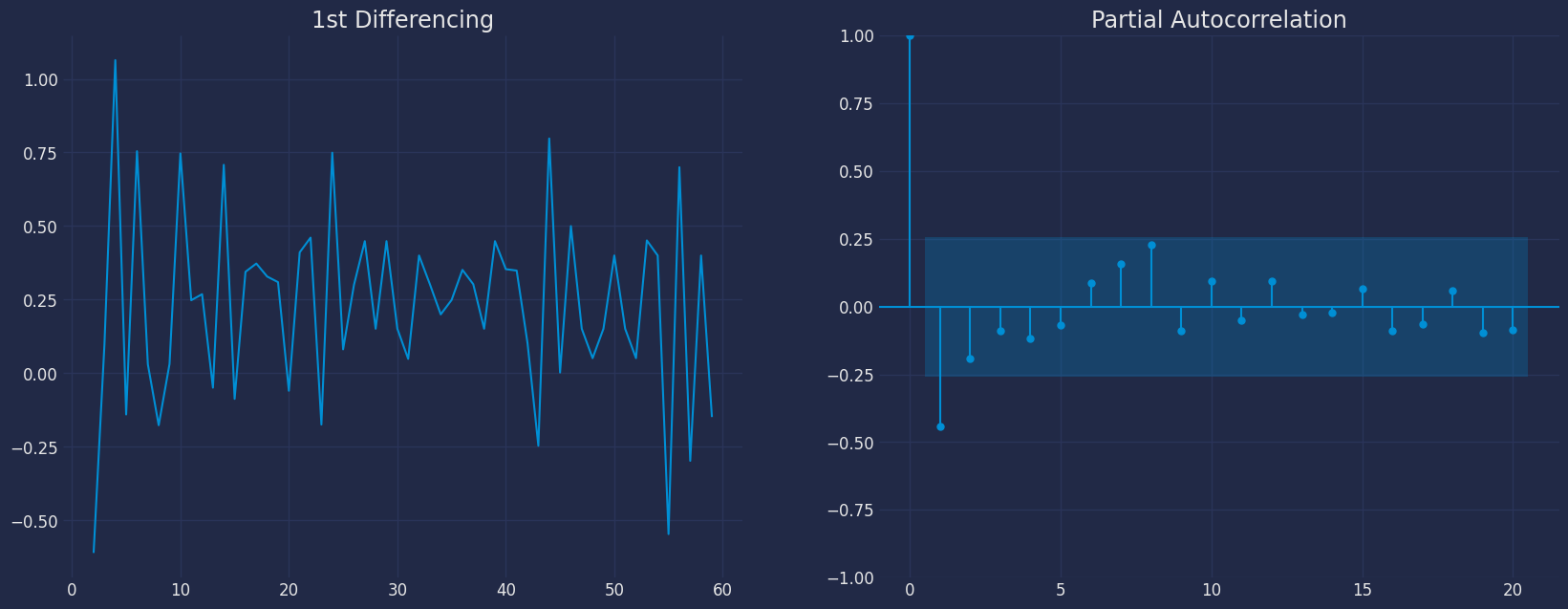

我们可以看到 PACF 的滞后 1 是相当显著的，因为它远高于显著性线。因此，我们将 p 的值固定为 1。

如何找到MA项的阶数(q)

就像我们查看PACF图来确定AR项的数量一样，我们将查看ACF图来确定MA项的数量。MA项技术上是滞后预测的误差。
ACF告诉我们需要多少个MA项来消除平稳序列中的自相关。
让我们来看一下差分序列的自相关图。

from statsmodels.graphics.tsaplots import plot_acf

fig, axes = plt.subplots(1, 2)
axes[0].plot(df1["y"].diff()); axes[0].set_title('1st Differencing')
axes[1].set(ylim=(0,1.2))
plot_acf(df["y"].diff().dropna(), ax=axes[1], lags=20)

plt.show()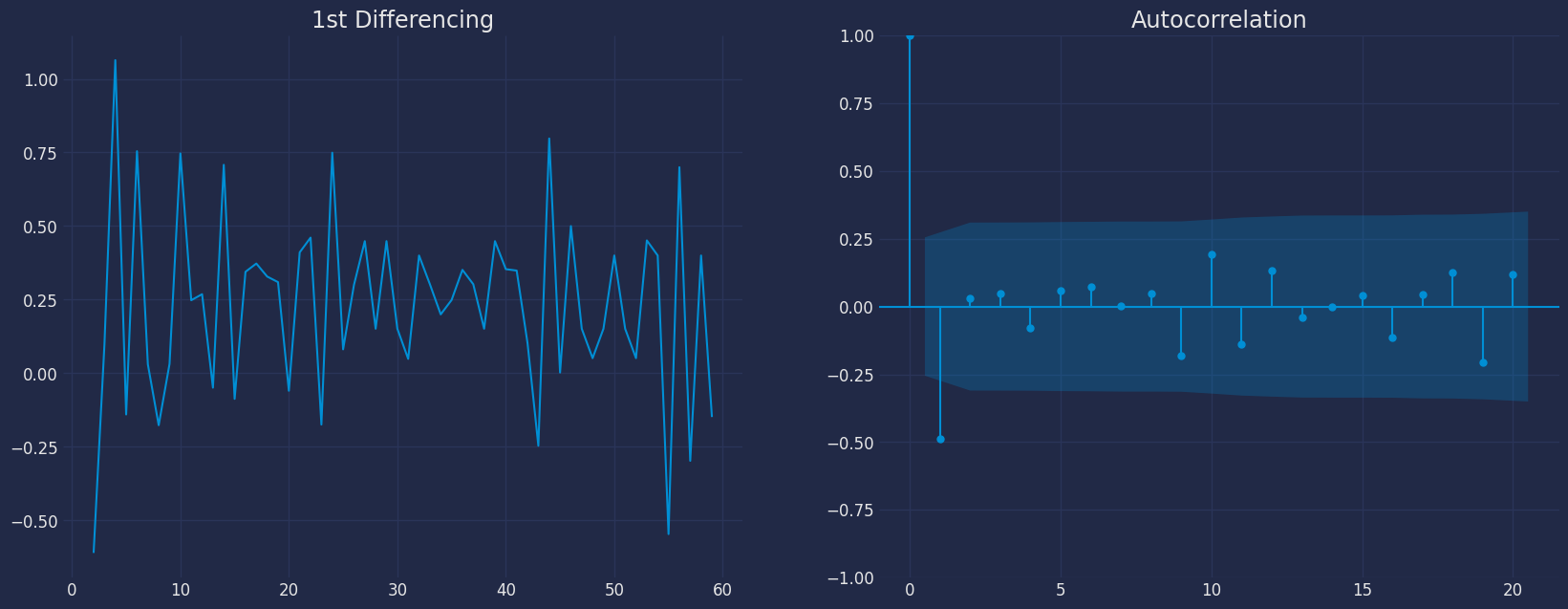

我们可以看到几个滞后值远高于显著性线。因此，我们将q固定为1。如果有任何疑问，我们将选择那个能够充分解释Y的更简单模型。

如何处理时间序列略微欠差分或过差分的情况

时间序列可能会出现略微欠差分的情况。再进行一次差分会导致略微过差分。
如果系列略微欠差分，通常添加一个或多个附加的自回归（AR）项可以解决。同样，如果略微过差分，我们可以尝试添加一个附加的移动平均（MA）项。

ARIMA的实现与StatsForecast

现在，我们已经确定了p、d和q的值。我们拥有了拟合ARIMA模型所需的所有内容。我们将使用statsforecast包中的ARIMA()实现。

找到的参数是： * 对于自回归模型，$p=1$ * 对于移动平均模型，$q=1$ * 以及具有差分的单位根模型的平稳性，$d=1$

因此，我们将要测试的模型是ARIMA(1,1,1)模型。

from statsforecast.models import ARIMA

为了进一步了解ARIMA模型的函数参数，以下是参数的列表。有关更多信息，请访问文档

order : tuple (默认=(0, 0, 0))
        ARIMA模型的非季节性部分的规格：三个组成部分(p, d, q)分别是自回归阶数、差分阶数和移动平均阶数。
    season_length : int (默认=1)
        每单位时间的观察次数。例如：24小时数据。
    seasonal_order : tuple (默认=(0, 0, 0))
        ARIMA模型的季节性部分的规格。
        (P, D, Q)分别是自回归阶数、差分阶数和移动平均阶数。
    include_mean : bool (默认=True)
        ARIMA模型是否应包含均值项？
        对于未差分的序列，默认值为True，对于已差分的序列，默认为False（在这种情况下，均值不会影响拟合或预测）。
    include_drift : bool (默认=False)
        ARIMA模型是否应包含线性漂移项？
        （即，拟合一个带有ARIMA误差的线性回归。）
    include_constant : bool，可选 (默认=None)
        如果为True，则在未差分的系列中设置include_mean为True，而在已差分的系列中设置include_drift为True。
        请注意，如果进行了一次以上的差分，无论此参数的值如何，都不包括常数。
        这是故意的，否则将引入二次及更高阶多项式趋势。
    blambda : float，可选 (默认=None)
        Box-Cox变换参数。
    biasadj : bool (默认=False)
        使用调整后的反变换均值Box-Cox。
    method : str (默认='CSS-ML')
        拟合方法：最大似然或最小化条件平方和。
        默认情况下（除非存在缺失值），使用条件平方和寻找初始值，然后使用最大似然。
    fixed : dict，可选 (默认=None)
        包含ARIMA模型固定系数的字典。例如：`{'ar1': 0.5, 'ma2': 0.75}`。
        对于自回归项使用`ar{i}`键。对于其季节版本使用`sar{i}`。
        对于移动平均项使用`ma{i}`键。对于其季节版本使用`sma{i}`。
        对于截距和漂移使用`intercept`和`drift`键。
        对于外生变量使用`ex_{i}`键。
    alias : str
        模型的自定义名称。
    prediction_intervals : Optional[ConformalIntervals]
        计算符合预测区间的信息。
        默认情况下，模型将计算原生预测
        区间。

实例化模型

arima = ARIMA(order=(1, 1, 1), season_length=1)

拟合模型

arima = arima.fit(y=df["y"].values)

进行预测

y_hat_dict = arima.predict(h=6,)
y_hat_dict

{'mean': array([83.20155301, 83.20016307, 83.20064702, 83.20047852, 83.20053719,
        83.20051676])}

我们可以通过添加置信区间来进行预测，例如95%。

y_hat_dict2 = arima.predict(h=6,level=[95])
y_hat_dict2

{'mean': array([83.20155301, 83.20016307, 83.20064702, 83.20047852, 83.20053719,
        83.20051676]),
 'lo-95': 0    82.399545
 1    82.072363
 2    81.820183
 3    81.607471
 4    81.420010
 5    81.250474
 Name: 95%, dtype: float64,
 'hi-95': 0    84.003561
 1    84.327963
 2    84.581111
 3    84.793486
 4    84.981064
 5    85.150560
 Name: 95%, dtype: float64}

你可以看到，通过 Arima 模型提取的预测结果或我们今后使用的任何其他方法的结果都是一个字典。要提取该结果，我们可以使用 .get() 函数，这将帮助我们提取我们使用的每种方法字典中每一部分的结果。

ARIMA.forecast 方法

内存高效的预测。

该方法避免了由于对象存储而带来的内存负担。它类似于 fit_predict，但不存储信息。它假设您提前知道预测范围。

Y_hat_df=arima.forecast(y=df["y"].values, h=6, fitted=True)
Y_hat_df

{'mean': array([83.20155301, 83.20016307, 83.20064702, 83.20047852, 83.20053719,
        83.20051676]),
 'fitted': array([69.05477857, 69.12394817, 69.75299437, 69.15912019, 69.24378043,
        70.30108758, 70.1768715 , 70.91580642, 70.95970624, 70.7809505 ,
        70.81126886, 71.55054441, 71.80679168, 72.07233443, 72.0279183 ,
        72.72583278, 72.65118662, 72.98674108, 73.36216446, 73.69027839,
        74.00014861, 73.94469901, 74.34873167, 74.8111531 , 74.64339332,
        75.37995777, 75.47302934, 75.76655702, 76.2158311 , 76.37025745,
        76.81458465, 76.97067731, 77.01897755, 77.41515795, 77.71998951,
        77.92034484, 78.16845267, 78.51873753, 78.82204435, 78.97468575,
        79.41961419, 79.77564854, 80.12368405, 80.2291665 , 79.9857536 ,
        80.77049462, 80.7862653 , 81.27613438, 81.43472012, 81.48459197,
        81.63513184, 82.03254064, 82.18745311, 82.23856226, 82.68528462,
        83.08738006, 82.55106033, 83.23355629, 82.95319957, 83.33949704])}

由于我们生成的预测结果是一个字典，为了利用这些结果，我们将其保存在 .DataFrame() 中。首先，我们将生成一系列日期，然后使用 .get() 函数提取预测结果，最后将它们进行合并并保存在一个 DataFrame 中。

forecast=pd.Series(pd.date_range("2014-01-01", freq="ys", periods=6))
forecast=pd.DataFrame(forecast)
forecast.columns=["ds"]
forecast

	ds
0	2014-01-01
1	2015-01-01
2	2016-01-01
3	2017-01-01
4	2018-01-01
5	2019-01-01

df=df.set_index("ds")

forecast["unique_id"]="1"
forecast["hat"]=y_hat_dict.get("mean")
forecast["lo-95"]=y_hat_dict2.get("lo-95")
forecast["hi-95"]=y_hat_dict2.get("hi-95")
forecast=forecast.set_index("ds")
forecast

	unique_id	hat	lo-95	hi-95
ds
2014-01-01	1	83.201553	82.399545	84.003561
2015-01-01	1	83.200163	82.072363	84.327963
2016-01-01	1	83.200647	81.820183	84.581111
2017-01-01	1	83.200479	81.607471	84.793486
2018-01-01	1	83.200537	81.420010	84.981064
2019-01-01	1	83.200517	81.250474	85.150560

一旦生成了预测，我们可以进行可视化，以查看我们模型生成的行为。

_, ax = plt.subplots(1, 1)
df_plot = pd.concat([df, forecast])
df_plot[['y', 'hat']].plot(ax=ax, linewidth=2)
ax.fill_between(df_plot.index, 
                df_plot['lo-95'], 
                df_plot['hi-95'],
                alpha=.35,
                color='orange',
                label='ARIMA-level-95')
ax.set_title('', fontsize=22)
ax.set_ylabel('', fontsize=20)
ax.set_xlabel('Timestamp [t]', fontsize=12)
ax.legend(prop={'size': 15})
ax.grid(True)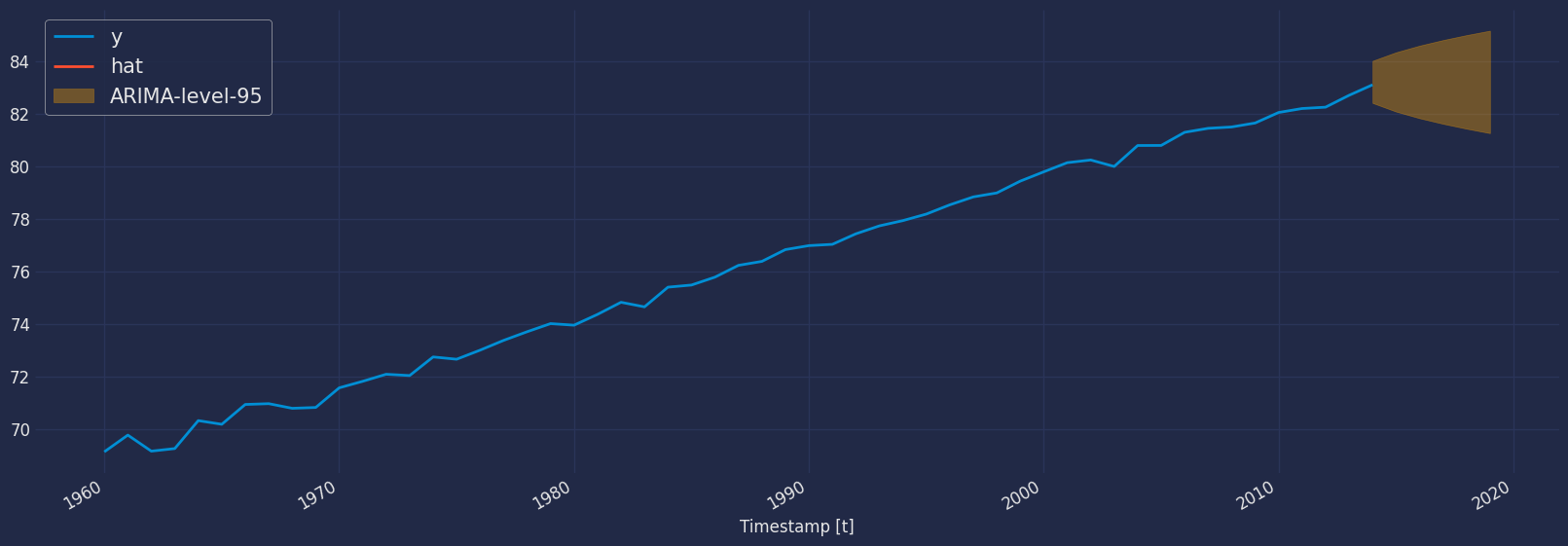

模型评估

常用的评估预测的准确性指标有：

平均绝对百分比误差 (MAPE)
平均误差 (ME)
平均绝对误差 (MAE)
平均百分比误差 (MPE)
均方根误差 (RMSE)
实际值与预测值之间的相关性 (corr)

df.reset_index("ds", inplace=True)
Y_train_df = df[df.ds<='2013-01-01'] 
Y_test_df = df[df.ds>'2013-01-01'] 

Y_train_df.shape, Y_test_df.shape

((54, 3), (6, 3))

from sklearn import metrics

def model_evaluation(y_true, y_pred, Model):
    
    def mean_absolute_percentage_error(y_true, y_pred): 
        y_true, y_pred = np.array(y_true), np.array(y_pred)
        return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
    print (f'Model Evaluation: {Model}')
    print(f'MSE is : {metrics.mean_squared_error(y_true, y_pred)}')
    print(f'MAE is : {metrics.mean_absolute_error(y_true, y_pred)}')
    print(f'RMSE is : {np.sqrt(metrics.mean_squared_error(y_true, y_pred))}')
    print(f'MAPE is : {mean_absolute_percentage_error(y_true, y_pred)}')
    print(f'R2 is : {metrics.r2_score(y_true, y_pred)}')
    print(f'corr is : {np.corrcoef(y_true, y_pred)[0,1]}',end='\n\n')

model_evaluation(Y_test_df["y"], forecast["hat"], "Arima")

Model Evaluation: Arima
MSE is : 0.08846533957222678
MAE is : 0.20228704669491057
RMSE is : 0.29743123503127034
MAPE is : 0.24430769688205894
R2 is : -0.2792859149048943
corr is : 0.3634615475289058

大约24.43%的平均绝对百分比误差（MAPE）意味着该模型在预测接下来的6个观察值时大约有75.57%的准确率。现在我们知道如何手动构建ARIMA模型。

感谢

我们要感谢Naren Castellon为我们撰写本教程。

参考文献

Nixtla-Arima
Rob J. Hyndman 和 George Athanasopoulos (2018). “预测原理与实践，时间序列交叉验证”。

Give us a ⭐ on Github

目录

介绍

ARIMA模型简介

ARIMA模型的类型

ARIMA模型中p、d和q的含义

p的含义

d的含义

q的含义

自回归和移动平均模型

自回归模型

移动平均模型

ARIMA模型

用语言描述ARIMA模型

如何在ARIMA模型中找到差分阶数(d)

加载库和数据

读取数据

使用plot方法探索数据

季节分解

加法时间序列

乘法时间序列

增强型迪基-福勒检验

如何找到AR项的阶数 (p)

如何找到MA项的阶数(q)

如何处理时间序列略微欠差分或过差分的情况

ARIMA的实现与StatsForecast

实例化模型

拟合模型

进行预测

ARIMA.forecast 方法

模型评估

感谢

参考文献