# 此单元格将不会被渲染,但用于隐藏警告并限制显示的行数。
import warnings
warnings.filterwarnings("ignore")
import logging
logging.getLogger('statsforecast').setLevel(logging.ERROR)
import pandas as pd
pd.set_option('display.max_rows', 6)简单指数平滑模型
使用
Statsforecast的SimpleExponentialSmoothing Model的逐步指南。
在这个演示中,我们将熟悉主要的 StatsForecast 类以及一些相关的方法,如 StatsForecast.plot、StatsForecast.forecast 和 StatsForecast.cross_validation 等。
目录
介绍
指数平滑法于20世纪50年代末提出(Brown,1959;Holt,1957;Winters,1960),并激励了一些最成功的预测方法。使用指数平滑法产生的预测是过去观测值的加权平均,权重随着观测值的时间推移而呈指数衰减。换句话说,最近的观测值权重更高。该框架能够快速生成可靠的预测,适用于广泛的时间序列,这为工业应用带来了极大的优势和重要性。
简易指数平滑模型是一种用于时间序列分析的方法,用于根据历史观测预测未来值。该模型基于这样一个思想,即时间序列的未来值将受到过去值的影响,并且随着时间的推移,过去值的影响将呈指数衰减。
简易指数平滑模型使用一个平滑因子,这是一个介于0和1之间的数字,表示在预测未来值时给予过去观测的相对重要性。值为1表示所有过去观测被给予相同的重要性,而值为0表示仅考虑最新的观测值。
简易指数平滑模型可以数学表示为:
\[\hat{y}_{T+1|T} = \alpha y_T + \alpha(1-\alpha) y_{T-1} + \alpha(1-\alpha)^2 y_{T-2}+ \cdots,\]
其中\(y_T\)是时期\(t\)的观测值,\(\hat{y}_{T+1|T}\)是下一时期的预测值,\(y_{T-1}\)是前一时期的观测值,\(\alpha\)是平滑因子。
简易指数平滑模型因其简单性和易用性而被广泛使用。然而,它也有其局限性,因为它无法捕捉数据中的复杂模式,并且不适用于具有趋势或季节性模式的时间序列。
简单指数平滑模型的建立
最简单的指数平滑方法自然被称为简单指数平滑(SES)。这种方法适用于没有明显趋势或季节模式的数据预测。
使用朴素方法,未来的所有预测都等于系列的最后观察值, \[\hat{y}_{T+h|T} = y_{T},\]
对于 \(h=1,2,\dots\)。因此,朴素方法假设最近的观察是唯一重要的,所有之前的观察对未来没有提供任何信息。这可以被看作是加权平均,其中所有的权重都赋予了最后的观察值。
使用平均方法,所有未来的预测都等于观察数据的简单平均值, \[\hat{y}_{T+h|T} = \frac1T \sum_{t=1}^T y_t,\]
对于 \(h=1,2,\dots\)。因此,平均方法假设所有观察值都同等重要,并在生成预测时赋予它们相等的权重。
我们通常希望在这两种极端之间选择。例如,给最近的观察值赋予更大的权重,可能比给遥远过去的观察值更为合理。这正是简单指数平滑背后的概念。预测是使用加权平均计算的,其中权重随着观察值越来越远而指数下降——权重最小的与最旧的观察值相关联:
\[\begin{equation} \hat{y}_{T+1|T} = \alpha y_T + \alpha(1-\alpha) y_{T-1} + \alpha(1-\alpha)^2 y_{T-2}+ \cdots, \tag{1} \end{equation}\]
其中 \(0 \le \alpha \le 1\) 是平滑参数。对于时间 \(T+1\) 的一步预测是系列 \(y_1,\dots,y_T\) 中所有观察值的加权平均。权重下降的速率由参数 \(\alpha\) 控制。
对于任意介于0和1之间的\(\alpha\),附加于观察值的权重随着时间的推移而呈指数下降,因此被称为“指数平滑”。如果\(\alpha\)很小(即接近0),则对更远过去的观察值赋予更多权重。如果\(\alpha\)很大(即接近1),则对最近的观察值赋予更多权重。在极端情况下,当\(\alpha=1\)时,\(\hat{y}_{T+1|T}=y_T\),预测值等于天真的预测值。
我们呈现两种简单指数平滑的等效形式,每种形式都会导致预测方程(1)。
加权平均形式
时间 \(T+1\) 的预测等于最近观察值 \(y_T\) 和之前预测值 \(\hat{y}_{T|T-1}\) 的加权平均:
\[\hat{y}_{T+1|T} = \alpha y_T + (1-\alpha) \hat{y}_{T|T-1},\]
其中 \(0 \le \alpha \le 1\) 是平滑参数。同样,我们可以将拟合值写为
\[\hat{y}_{t+1|t} = \alpha y_t + (1-\alpha) \hat{y}_{t|t-1},\]
对于 \(t=1,\dots,T\)。(请记住,拟合值仅仅是训练数据的一步预测。)
这一过程必须从某个地方开始,因此我们让时间 1 的第一个拟合值用 \(\ell_{0}\) 表示(我们需要估计它)。然后
\[\begin{align*} \hat{y}_{2|1} &= \alpha y_1 + (1-\alpha) \ell_0\\ \hat{y}_{3|2} &= \alpha y_2 + (1-\alpha) \hat{y}_{2|1}\\ \hat{y}_{4|3} &= \alpha y_3 + (1-\alpha) \hat{y}_{3|2}\\ \vdots\\ \hat{y}_{T|T-1} &= \alpha y_{T-1} + (1-\alpha) \hat{y}_{T-1|T-2}\\ \hat{y}_{T+1|T} &= \alpha y_T + (1-\alpha) \hat{y}_{T|T-1}. \end{align*}\]
将每个方程代入以下方程,我们得到
\[\begin{align*} \hat{y}_{3|2} & = \alpha y_2 + (1-\alpha) \left[\alpha y_1 + (1-\alpha) \ell_0\right] \\ & = \alpha y_2 + \alpha(1-\alpha) y_1 + (1-\alpha)^2 \ell_0 \\ \hat{y}_{4|3} & = \alpha y_3 + (1-\alpha) [\alpha y_2 + \alpha(1-\alpha) y_1 + (1-\alpha)^2 \ell_0]\\ & = \alpha y_3 + \alpha(1-\alpha) y_2 + \alpha(1-\alpha)^2 y_1 + (1-\alpha)^3 \ell_0 \\ & ~~\vdots \\ \hat{y}_{T+1|T} & = \sum_{j=0}^{T-1} \alpha(1-\alpha)^j y_{T-j} + (1-\alpha)^T \ell_{0}. \end{align*}\]
对于大的 \(T\),最后一项变得微不足道。因此,加权平均形式导致与预测方程 (1) 相同的结果。
组件形式
另一种表示方式是组件形式。对于简单指数平滑,唯一包含的组件是水平 \(\ell_{t}\)。指数平滑方法的组件形式表示包括一个预测方程和一个平滑方程,分别对应于方法中包含的每个组件。简单指数平滑的组件形式如下所示:
\[\begin{align*} \text{预测方程} && \hat{y}_{t+h|t} & = \ell_{t}\\ \text{平滑方程} && \ell_{t} & = \alpha y_{t} + (1 - \alpha)\ell_{t-1}, \end{align*}\]
其中 \(\ell_{t}\) 是时间 \(t\) 的序列水平(或平滑值)。将 \(h=1\) 置入将得到拟合值,而将 \(t=T\) 置入则给出训练数据之外的真实预测。
预测方程显示时间 \(t+1\) 的预测值是时间 \(t\) 的估计水平。水平的平滑方程(通常称为水平方程)给出每个时间 \(t\) 的序列估计水平。
如果我们在平滑方程中用 \(\hat{y}_{t+1|t}\) 替换 \(\ell_{t}\),用 \(\hat{y}_{t|t-1}\) 替换 \(\ell_{t-1}\),我们将恢复简单指数平滑的加权平均形式。
简单指数平滑的组件形式本身并不是特别有用,但当我们开始添加其他组件时,这将是最易于使用的形式。
平滑预测
简单指数平滑具有“平坦”的预测函数:
\[\hat{y}_{T+h|T} = \hat{y}_{T+1|T}=\ell_T, \qquad h=2,3,\dots.\]
也就是说,所有的预测都取相同的值,等于最后一个水平分量。请记住,这些预测只有在时间序列没有趋势或季节性成分时才适用。
加载库和数据
将需要使用Statsforecast。要安装,请参见说明。
接下来,我们导入绘图库并配置绘图样式。
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plt.style.use('grayscale') # 五三八 灰度 经典
plt.rcParams['lines.linewidth'] = 1.5
dark_style = {
'figure.facecolor': '#008080', # #212946
'axes.facecolor': '#008080',
'savefig.facecolor': '#008080',
'axes.grid': True,
'axes.grid.which': 'both',
'axes.spines.left': False,
'axes.spines.right': False,
'axes.spines.top': False,
'axes.spines.bottom': False,
'grid.color': '#000000', #2A3459
'grid.linewidth': '1',
'text.color': '0.9',
'axes.labelcolor': '0.9',
'xtick.color': '0.9',
'ytick.color': '0.9',
'font.size': 12 }
plt.rcParams.update(dark_style)
from pylab import rcParams
rcParams['figure.figsize'] = (18,7)import pandas as pd
df=pd.read_csv("https://raw.githubusercontent.com/Naren8520/Serie-de-tiempo-con-Machine-Learning/main/Data/ads.csv")
df.head()| Time | Ads | |
|---|---|---|
| 0 | 2017-09-13T00:00:00 | 80115 |
| 1 | 2017-09-13T01:00:00 | 79885 |
| 2 | 2017-09-13T02:00:00 | 89325 |
| 3 | 2017-09-13T03:00:00 | 101930 |
| 4 | 2017-09-13T04:00:00 | 121630 |
StatsForecast 的输入始终是一个长格式的数据框,包含三列:unique_id,ds 和 y:
unique_id(字符串、整数或类别)表示序列的标识符。ds(日期戳)列应该是 Pandas 期望的格式,理想情况下,日期为 YYYY-MM-DD,时间戳为 YYYY-MM-DD HH:MM:SS。y(数字)表示我们希望进行预测的测量值。
df["unique_id"]="1"
df.columns=["ds", "y", "unique_id"]
df| ds | y | unique_id | |
|---|---|---|---|
| 0 | 2017-09-13T00:00:00 | 80115 | 1 |
| 1 | 2017-09-13T01:00:00 | 79885 | 1 |
| 2 | 2017-09-13T02:00:00 | 89325 | 1 |
| ... | ... | ... | ... |
| 213 | 2017-09-21T21:00:00 | 103080 | 1 |
| 214 | 2017-09-21T22:00:00 | 95155 | 1 |
| 215 | 2017-09-21T23:00:00 | 80285 | 1 |
216 rows × 3 columns
print(df.dtypes)ds object
y int64
unique_id object
dtype: objectdf["ds"] = pd.to_datetime(df["ds"])使用plot方法探索数据
使用StatsForecast类中的plot方法绘制一些系列。该方法从数据集中随机打印一个系列,对于基础的EDA非常有用。
from statsforecast import StatsForecast
StatsForecast.plot(df)
自相关图
fig, axs = plt.subplots(nrows=1, ncols=2)
plot_acf(df["y"], lags=30, ax=axs[0],color="fuchsia")
axs[0].set_title("Autocorrelation");
# 格拉菲科
plot_pacf(df["y"], lags=30, ax=axs[1],color="lime")
axs[1].set_title('Partial Autocorrelation')
#plt.savefig("Gráfico de Densidad y qq")
plt.show();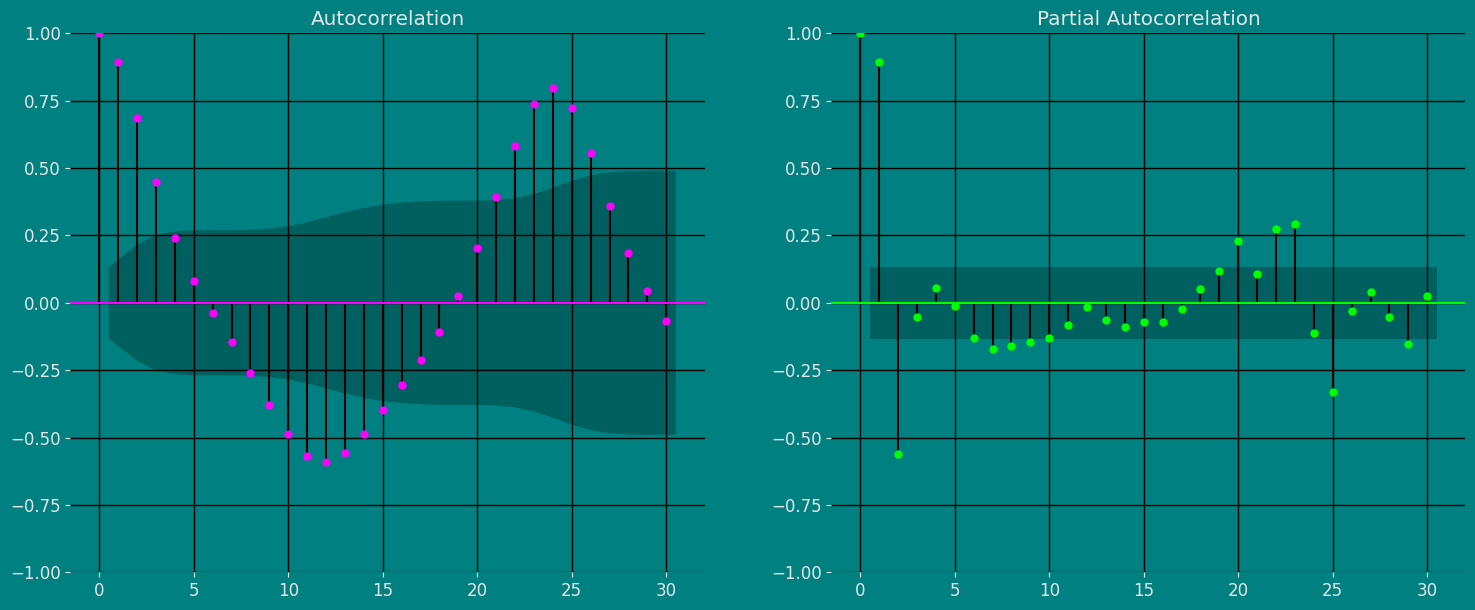
将数据分为训练集和测试集
让我们将数据划分为不同的集合
- 用于训练我们的
简单指数平滑 (SES)的数据。 - 用于测试我们模型的数据。
对于测试数据,我们将使用最后30小时的数据来测试和评估我们模型的性能。
train = df[df.ds<='2017-09-20 17:00:00']
test = df[df.ds>'2017-09-20 17:00:00'] train.shape, test.shape((186, 3), (30, 3))现在让我们绘制训练数据和测试数据。
sns.lineplot(train,x="ds", y="y", label="Train", linestyle="--")
sns.lineplot(test, x="ds", y="y", label="Test")
plt.title("Ads watched (hourly data)");
plt.show()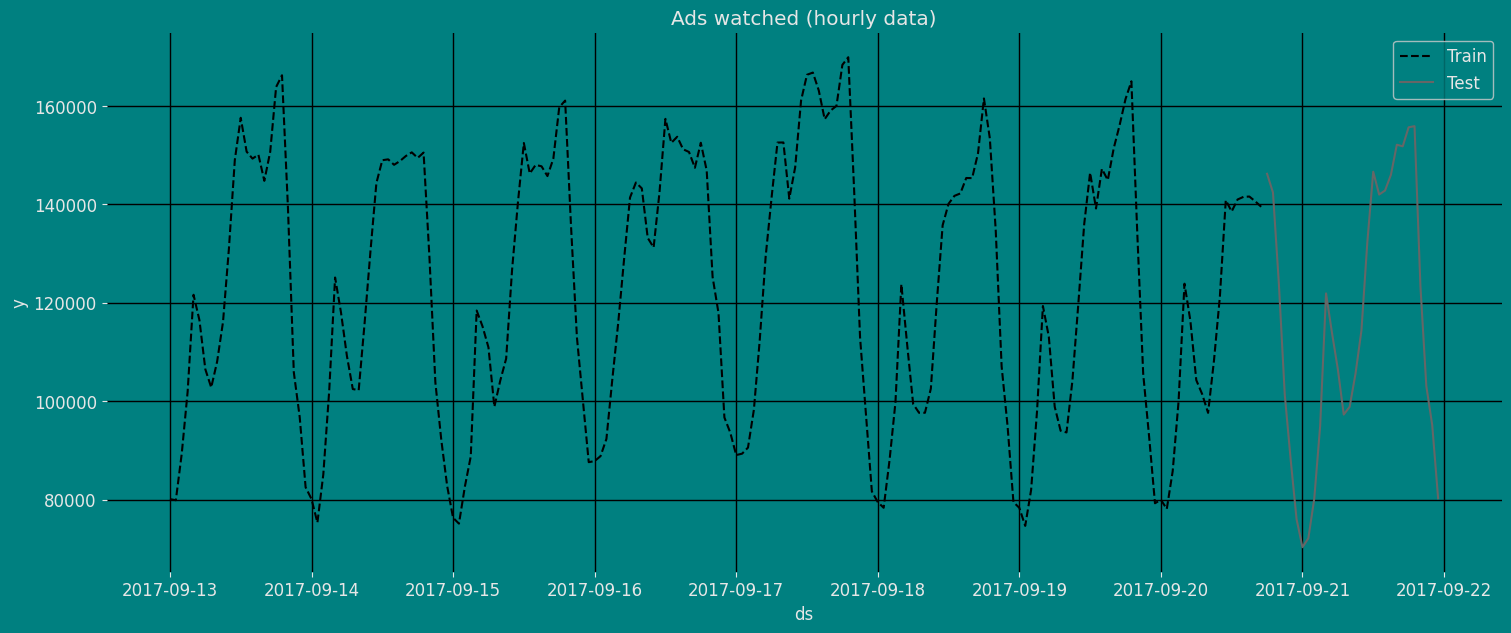
使用StatsForecast实现简单指数平滑
要了解SimpleExponentialSmoothing Model函数的参数,以下是列出的详细信息。有关更多信息,请访问文档。
alpha : float
平滑参数。
alias : str
模型的自定义名称。
prediction_intervals : Optional[ConformalIntervals]
用于计算符合预测区间的信息。
默认情况下,模型将计算原生预测
区间。加载库
from statsforecast import StatsForecast
from statsforecast.models import SimpleExponentialSmoothing实例化模型
我们将为不同的 alpha 值构建不同的模型。
horizon = len(test)
# 我们称之为即将使用的模型
models = [SimpleExponentialSmoothing(alpha=0.1, alias="SES01"),
SimpleExponentialSmoothing(alpha=0.5,alias="SES05"),
SimpleExponentialSmoothing(alpha=0.8,alias="SES08")
]我们通过实例化一个新的 StatsForecast 对象来拟合模型,使用以下参数:
模型:模型的列表。选择你想要的模型并导入它们。
freq:一个字符串,表示数据的频率。(查看 pandas 的可用频率)n_jobs:n_jobs: int,进行并行处理时使用的作业数量,使用 -1 表示使用所有核心。fallback_model:如果一个模型失败,使用的备用模型。
任何设置都会传入构造函数。然后你调用它的 fit 方法并传入历史数据框。
sf = StatsForecast(df=df,
models=models,
freq='H', # 每小时频率
n_jobs=-1)拟合模型
sf.fit()StatsForecast(models=[SES01,SES05,SES08])让我们看看我们简单的简单指数平滑模型 (SES) 的结果。我们可以通过以下指令来观察它:
result01=sf.fitted_[0,0].model_
result05=sf.fitted_[0,1].model_
result08=sf.fitted_[0,2].model_
result01{'mean': array([120864.91], dtype=float32),
'fitted': array([ nan, 80115. , 80092. , 81015.3 , 83106.77 ,
86959.09 , 89910.69 , 91569.12 , 92691.7 , 94228.03 ,
96417.73 , 99878.96 , 104793.06 , 110072.76 , 114136.98 ,
117652.78 , 120897.5 , 123285.75 , 126026.18 , 129807.56 ,
133450.3 , 134057.28 , 131241.05 , 127794.945, 123267.445,
118953.2 , 114591.38 , 111642.74 , 110686.47 , 112131.32 ,
112721.19 , 112371.57 , 111381.914, 110467.73 , 111004.95 ,
112958.45 , 116095.11 , 119382.6 , 122359.336, 124927.41 ,
127315.664, 129567.1 , 131667.39 , 133444.66 , 135152.19 ,
134549.97 , 131476.47 , 127546.32 , 123068.19 , 118392.875,
114066.586, 110923.92 , 108711.03 , 109682.93 , 110233.64 ,
110304.27 , 109159.84 , 108662.36 , 108662.625, 110460.36 ,
113457.83 , 117359.05 , 120250.64 , 123027.58 , 125498.32 ,
127523.484, 129699.64 , 132702.17 , 135540.45 , 135538.4 ,
133279.06 , 129971.164, 125735.55 , 121945.49 , 118635.445,
116006.9 , 114852.71 , 114961.44 , 116360.3 , 118862.766,
121420.484, 123603.44 , 124562.09 , 125229.88 , 126954.9 ,
129996.91 , 132247.22 , 134396. , 136075.89 , 137532.81 ,
138523.03 , 139923.22 , 140618.4 , 139081.06 , 136965.45 ,
132938.9 , 129006.016, 125011.414, 121444.77 , 118357.8 ,
116351.016, 115972.914, 117322.625, 119730.86 , 123013.77 ,
125970.4 , 127490.36 , 129496.32 , 132657.69 , 136025.42 ,
139100.88 , 141504.8 , 143084.81 , 144681.83 , 146215.64 ,
148428.58 , 150575.72 , 149789.16 , 146105.73 , 141229.66 ,
135274.2 , 129697.77 , 124563. , 120911.2 , 118799.08 ,
119297.17 , 118499.95 , 116593.96 , 114700.06 , 112995.555,
111952.5 , 112750.25 , 115050.73 , 117557.66 , 119974.89 ,
122199.4 , 124515.46 , 126597.414, 128978.67 , 132232.81 ,
134351.03 , 134387.92 , 131655.62 , 127994.57 , 123146.61 ,
118665.445, 114265.91 , 111038.31 , 109729.484, 110691.03 ,
110933.43 , 109728.086, 108155.28 , 106705.75 , 106453.68 ,
107783.305, 110603.98 , 114189.08 , 116686.67 , 119740.51 ,
122259.95 , 125170.96 , 128261.86 , 131574.17 , 134917.77 ,
134834.98 , 131909.98 , 128004.484, 123131.04 , 118815.94 ,
114745.34 , 111849.305, 110665.375, 111986.836, 112421.66 ,
111608.49 , 110591.64 , 109295.98 , 109192.875, 110398.59 ,
113443.734, 115954.86 , 118458.375, 120765.04 , 122847.53 ,
124623.78 , 126112.9 , 128123.11 , 129553.3 , 128992.47 ,
126229.23 , 122423.3 , 117785.97 , 113040.875, 108951.79 ,
106076.11 , 104963. , 106657.695, 107386.93 , 107297.734,
106296.96 , 105553.266, 105561.44 , 106443.3 , 109032.47 ,
112792.22 , 115712.5 , 118422.75 , 121182.47 , 124276.23 ,
127027.6 , 129891.34 , 132491.2 , 131581.6 , 128731.43 ,
125373.79 ], dtype=float32)}正如我们所见,上述结果以字典的形式输出,为了从字典中提取每个元素,我们将使用 .get() 函数提取元素,然后将其保存到 pd.DataFrame() 中。
fitted=pd.DataFrame(result01.get("fitted"), columns=["fitted01"])
fitted["fitted05"]=result05.get("fitted")
fitted["fitted08"]=result08.get("fitted")
fitted["ds"]=df["ds"]
fitted| fitted01 | fitted05 | fitted08 | ds | |
|---|---|---|---|---|
| 0 | NaN | NaN | NaN | 2017-09-13 00:00:00 |
| 1 | 80115.000000 | 80115.000000 | 80115.000000 | 2017-09-13 01:00:00 |
| 2 | 80092.000000 | 80000.000000 | 79931.000000 | 2017-09-13 02:00:00 |
| ... | ... | ... | ... | ... |
| 213 | 131581.593750 | 138842.562500 | 129852.359375 | 2017-09-21 21:00:00 |
| 214 | 128731.429688 | 120961.281250 | 108434.468750 | 2017-09-21 22:00:00 |
| 215 | 125373.789062 | 108058.140625 | 97810.890625 | 2017-09-21 23:00:00 |
216 rows × 4 columns
sns.lineplot(df, x="ds", y="y", label="Actual", linewidth=2)
sns.lineplot(fitted,x="ds", y="fitted01", label="Fitted01", linestyle="--", )
sns.lineplot(fitted, x="ds", y="fitted05", label="Fitted05", color="lime")
sns.lineplot(fitted, x="ds", y="fitted08", label="Fitted08")
plt.title("Ads watched (hourly data)");
plt.show()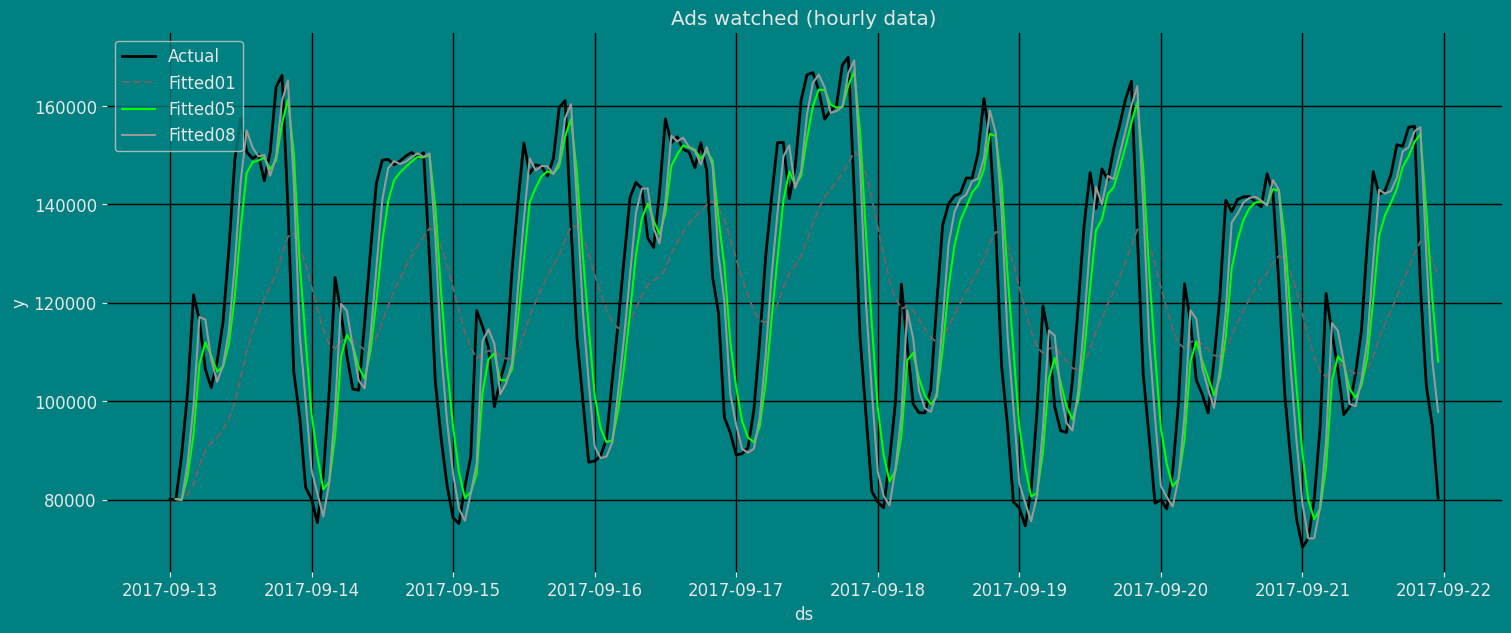
预测方法
如果你想在有多个序列或模型的生产环境中提高速度,我们建议使用 StatsForecast.forecast 方法,而不是 .fit 和 .predict。
主要区别在于 .forecast 不会存储拟合值,并且在分布式环境中具有高度可扩展性。
预测方法有两个参数:预测下一个 h(时间范围)和 level。
h (int):表示预测未来 h 步。在这种情况下,代表30小时后的预测。
这里的预测对象是一个新的数据框,包括一个模型名称的列和 y hat 值,以及不确定性区间的列。根据你的计算机,执行此步骤大约需要1分钟。
# 预测
Y_hat = sf.forecast(h=horizon, fitted=True)
Y_hat.head()| ds | SES01 | SES05 | SES08 | |
|---|---|---|---|---|
| unique_id | ||||
| 1 | 2017-09-22 00:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-22 01:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-22 02:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-22 03:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-22 04:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
values=sf.forecast_fitted_values()
values.head()| ds | y | SES01 | SES05 | SES08 | |
|---|---|---|---|---|---|
| unique_id | |||||
| 1 | 2017-09-13 00:00:00 | 80115.0 | NaN | NaN | NaN |
| 1 | 2017-09-13 01:00:00 | 79885.0 | 80115.000000 | 80115.00 | 80115.000000 |
| 1 | 2017-09-13 02:00:00 | 89325.0 | 80092.000000 | 80000.00 | 79931.000000 |
| 1 | 2017-09-13 03:00:00 | 101930.0 | 81015.296875 | 84662.50 | 87446.203125 |
| 1 | 2017-09-13 04:00:00 | 121630.0 | 83106.773438 | 93296.25 | 99033.242188 |
StatsForecast.plot(values)
Y_hat=Y_hat.reset_index()
Y_hat.head()| unique_id | ds | SES01 | SES05 | SES08 | |
|---|---|---|---|---|---|
| 0 | 1 | 2017-09-22 00:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 1 | 2017-09-22 01:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 2 | 1 | 2017-09-22 02:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 3 | 1 | 2017-09-22 03:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 4 | 1 | 2017-09-22 04:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
预测方法
要生成预测,请使用预测方法。
预测方法需要两个参数:预测下一个 h(表示时间范围)。 * h (int): 表示预测 \(h\) 个步骤进入未来。在本例中,表示提前 30 小时。
这里的预测对象是一个新的数据框,其中包括一个包含模型名称的列和 y hat 值,以及不确定性区间的列。
此步骤应少于 1 秒。
forecast_df = sf.predict(h=horizon)
forecast_df| ds | SES01 | SES05 | SES08 | |
|---|---|---|---|---|
| unique_id | ||||
| 1 | 2017-09-22 00:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-22 01:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-22 02:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| ... | ... | ... | ... | ... |
| 1 | 2017-09-23 03:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-23 04:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
| 1 | 2017-09-23 05:00:00 | 120864.90625 | 94171.570312 | 83790.179688 |
30 rows × 4 columns
我们可以使用 pandas 函数 pd.concat() 将预测结果与历史数据连接,然后能够使用该结果进行绘图。
df_plot=pd.concat([df, forecast_df]).set_index('ds')
df_plot| y | unique_id | SES01 | SES05 | SES08 | |
|---|---|---|---|---|---|
| ds | |||||
| 2017-09-13 00:00:00 | 80115.0 | 1 | NaN | NaN | NaN |
| 2017-09-13 01:00:00 | 79885.0 | 1 | NaN | NaN | NaN |
| 2017-09-13 02:00:00 | 89325.0 | 1 | NaN | NaN | NaN |
| ... | ... | ... | ... | ... | ... |
| 2017-09-23 03:00:00 | NaN | NaN | 120864.90625 | 94171.570312 | 83790.179688 |
| 2017-09-23 04:00:00 | NaN | NaN | 120864.90625 | 94171.570312 | 83790.179688 |
| 2017-09-23 05:00:00 | NaN | NaN | 120864.90625 | 94171.570312 | 83790.179688 |
246 rows × 5 columns
# 绘制数据及其指数平滑后的数据
plt.plot(df_plot['y'],label="Actual", linewidth=2.5)
plt.plot(df_plot['SES01'], label="Predict-SES01")
plt.plot(df_plot['SES05'], label="Predict-SES05")
plt.plot(df_plot['SES08'], label="Predicti-SES08")
sns.lineplot(fitted,x="ds", y="fitted01", label="Fitted01", linestyle="--", ) # '-', '--', '-.', ':',
sns.lineplot(fitted, x="ds", y="fitted05", label="Fitted05", color="yellow", linestyle="-.",)
sns.lineplot(fitted, x="ds", y="fitted08", label="Fitted08", color="fuchsia" ,linestyle=":")
plt.title("Ads watched (hourly data)");
plt.ylabel("")Text(0, 0.5, '')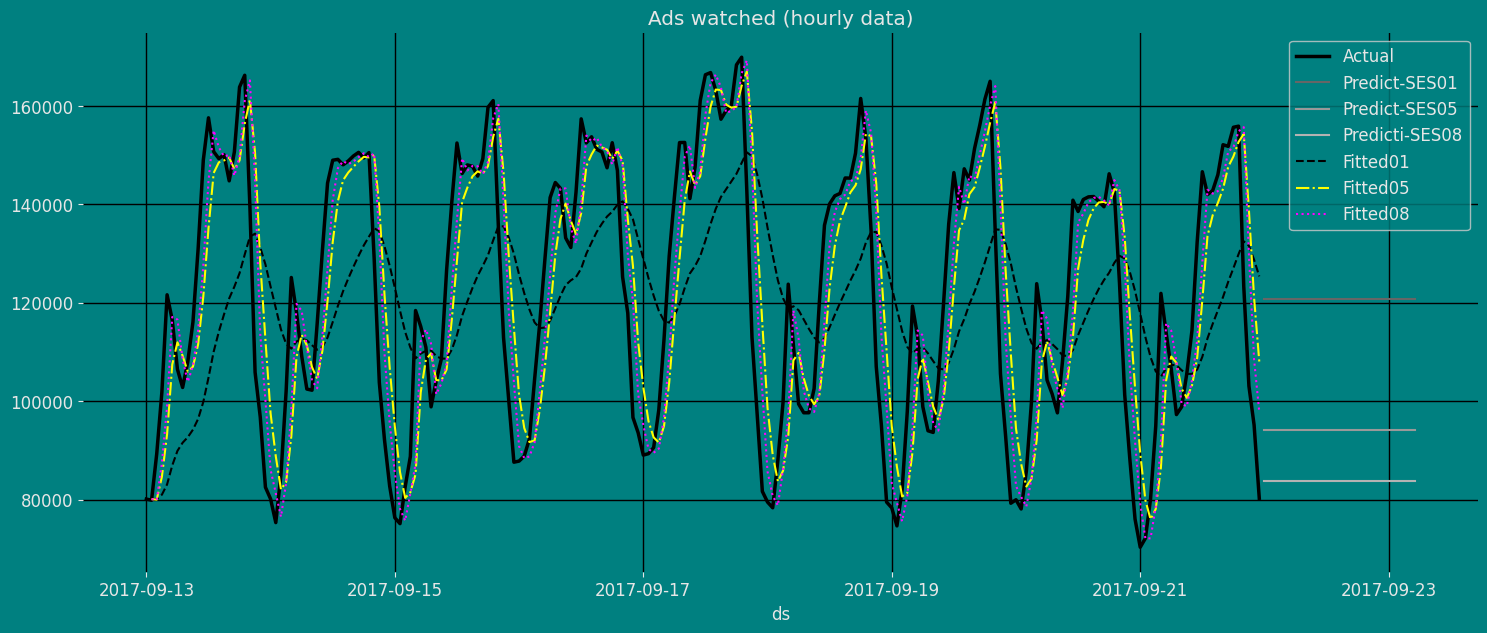
让我们使用Statsforecast中的plot函数绘制相同的图形,如下所示。
sf.plot(df, forecast_df)
交叉验证
在前面的步骤中,我们利用历史数据来预测未来。然而,为了评估其准确性,我们也希望了解模型在过去的表现。为了评估模型在数据上的准确性和稳健性,可以进行交叉验证。
对于时间序列数据,交叉验证的方法是通过在历史数据上定义一个滑动窗口,并预测随后的时间段。这种交叉验证形式使我们能够更好地估计模型在更广泛时间实例中的预测能力,同时保持训练集中的数据是连续的,这是我们的模型所要求的。
下图展示了这种交叉验证策略:
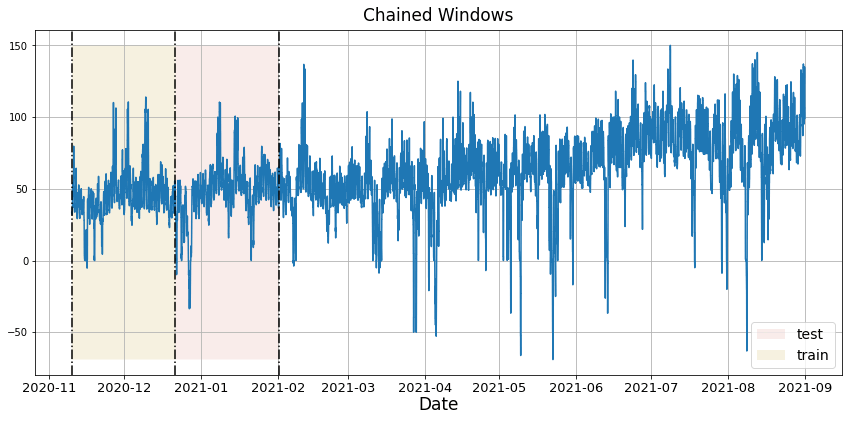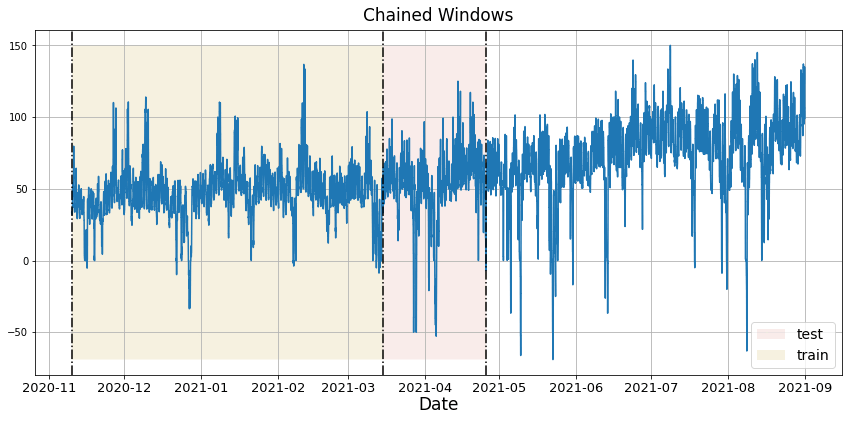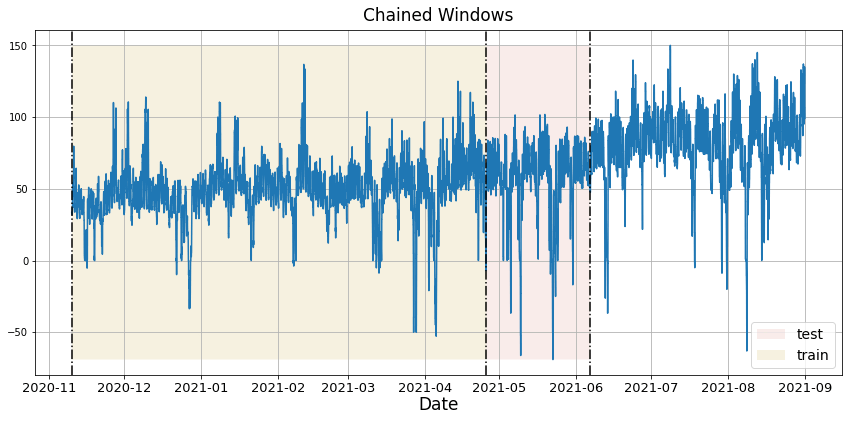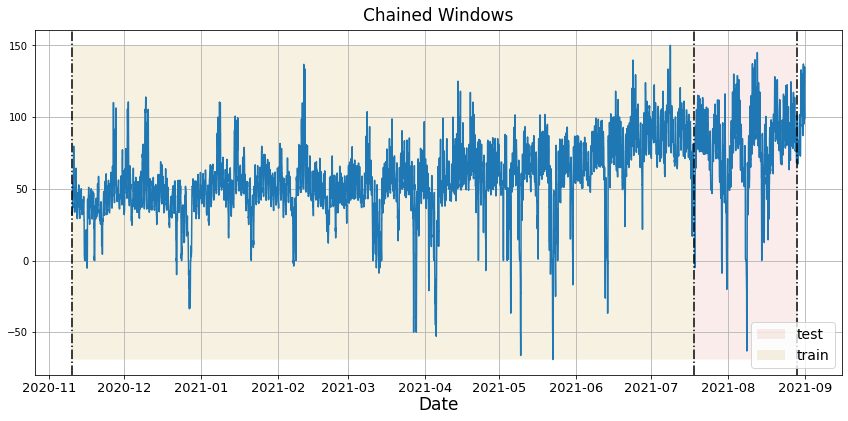
执行时间序列交叉验证
时间序列模型的交叉验证被视为最佳实践,但大多数实现都非常慢。statsforecast库将交叉验证实现为分布式操作,从而使过程更省时。如果您有大数据集,还可以使用Ray、Dask或Spark在分布式集群中执行交叉验证。
在这种情况下,我们希望评估每个模型在最后30个小时的性能(n_windows=),每隔两个月进行一次预测(step_size=30)。根据您的计算机情况,此步骤大约需要1分钟。
StatsForecast类中的cross_validation方法接受以下参数。
df:训练数据框h (int):表示被预测的未来h步。在这种情况下,即30小时。step_size (int):每个窗口之间的步长。换句话说:您希望多频繁地运行预测过程。n_windows(int):用于交叉验证的窗口数量。换句话说:您希望评估过去多少个预测过程。
crossvalidation_df = sf.cross_validation(df=df,
h=horizon,
step_size=30,
n_windows=3)crossvaldation_df对象是一个新的数据框,其中包含以下列:
unique_id:索引。如果您不喜欢使用索引,只需运行crossvalidation_df.resetindex()。ds:日期戳或时间索引cutoff:n_windows的最后日期戳或时间索引。y:真实值model:包含模型名称和拟合值的列。
crossvalidation_df| ds | cutoff | y | SES01 | SES05 | SES08 | |
|---|---|---|---|---|---|---|
| unique_id | ||||||
| 1 | 2017-09-18 06:00:00 | 2017-09-18 05:00:00 | 99440.0 | 118499.953125 | 109816.250 | 112747.695312 |
| 1 | 2017-09-18 07:00:00 | 2017-09-18 05:00:00 | 97655.0 | 118499.953125 | 109816.250 | 112747.695312 |
| 1 | 2017-09-18 08:00:00 | 2017-09-18 05:00:00 | 97655.0 | 118499.953125 | 109816.250 | 112747.695312 |
| ... | ... | ... | ... | ... | ... | ... |
| 1 | 2017-09-21 21:00:00 | 2017-09-20 17:00:00 | 103080.0 | 126112.898438 | 140008.125 | 139770.906250 |
| 1 | 2017-09-21 22:00:00 | 2017-09-20 17:00:00 | 95155.0 | 126112.898438 | 140008.125 | 139770.906250 |
| 1 | 2017-09-21 23:00:00 | 2017-09-20 17:00:00 | 80285.0 | 126112.898438 | 140008.125 | 139770.906250 |
90 rows × 6 columns
评估模型
现在我们可以使用合适的准确性指标来计算预测的准确性。在这里我们将使用均方根误差(RMSE)。为此,我们首先需要安装datasetsforecast,这是一个由Nixtla开发的Python库,其中包含计算RMSE的函数。
%%capture
!pip install datasetsforecastfrom datasetsforecast.losses import rmse计算RMSE的函数有两个参数:
- 实际值。
- 预测值,在这种情况下是
简单指数平滑模型(SES)。
from datasetsforecast.losses import mse, mae, rmse
def evaluate_cross_validation(df, metric):
models = df.drop(columns=['ds', 'cutoff', 'y']).columns.tolist()
evals = []
for model in models:
eval_ = df.groupby(['unique_id', 'cutoff']).apply(lambda x: metric(x['y'].values, x[model].values)).to_frame() # 计算每个唯一标识符、模型和截止时间的损失。
eval_.columns = [model]
evals.append(eval_)
evals = pd.concat(evals, axis=1)
evals = evals.groupby(['unique_id']).mean(numeric_only=True) # 对每种模型和unique_id组合的所有截止值的误差指标取平均值。
evals['best_model'] = evals.idxmin(axis=1)
return evalsevaluation_df = evaluate_cross_validation(crossvalidation_df, rmse)
evaluation_df| SES01 | SES05 | SES08 | best_model | |
|---|---|---|---|---|
| unique_id | ||||
| 1 | 27676.533203 | 29132.158203 | 29308.0 | SES01 |
致谢
我们要感谢 Naren Castellon 撰写本教程。
参考文献
- 黄昌泉 • 阿拉·佩图欣娜. 斯普林格系列 (2022). 使用Python进行应用时间序列分析与预测.
- 詹姆斯·D·汉密尔顿. 时间序列分析 普林斯顿大学出版社, 新泽西州普林斯顿, 第一版, 1994.
- Nixtla 参数.
- Pandas 可用频率.
- 罗布·J·海因德曼与乔治·阿萨纳索普洛斯 (2018). “预测原理与实践,时间序列交叉验证”。.
- 季节性周期 - 罗布·J·海因德曼.
Give us a ⭐ on Github