# 这是将Plotly图表渲染为HTML的操作。
# 更多信息,请参阅 https://quarto.org/docs/interactive/widgets/jupyter.html#plotly
import plotly.io as pio
pio.renderers.default = "plotly_mimetype+notebook_connected"
import warnings
warnings.simplefilter('ignore')
import logging
logging.getLogger('statsforecast').setLevel(logging.ERROR)电力负荷预测
在这个例子中,我们将展示如何进行电力负荷预测,考虑一个能够处理多重季节性(MSTL)的模型。
介绍
一些时间序列是从非常低频的数据生成的。这些数据通常表现出多重季节性。例如,按小时的数据可能会在每小时(每24个观测值)或每天(每24 * 7,即每天的观测值)中展现重复的模式。这就是电力负荷的情况。电力负荷可能会随小时变化,例如,在晚上,人们可能会期待电力消费增加。但电力负荷也会随着周的变化而变化。也许在周末,会有电力活动的增加。
在这个例子中,我们将展示如何对时间序列的两种季节性进行建模,以在短时间内生成准确的预测。我们将使用每小时的PJM电力负荷数据。原始数据可以在这里找到。
库
在这个示例中,我们将使用以下库:
StatsForecast。使用统计和计量经济模型进行Lightning ⚡️ 快速预测。包含用于多个季节性的MSTL模型。DatasetsForecast。用于评估预测的性能。Prophet。由Facebook开发的基准模型。NeuralProphet。Prophet的深度学习版本。用作基准。
%%capture
!pip install statsforecast
!pip install datasetsforecast
!pip install prophet
!pip install "neuralprophet[live]"使用多重季节性进行预测
电力负荷数据
根据数据集页面,
PJM Interconnection LLC(PJM)是美国的一个区域传输组织(RTO)。它是东部互联电网的一部分,运营着一个电力传输系统,服务于德拉瓦州、伊利诺伊州、印第安纳州、肯塔基州、马里兰州、密歇根州、新泽西州、北卡罗来纳州、俄亥俄州、宾夕法尼亚州、田纳西州、弗吉尼亚州、西弗吉尼亚州以及哥伦比亚特区的全部或部分地区。每小时的电力消耗数据来自PJM的网站,单位为兆瓦(MW)。
让我们来看看数据。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
pd.plotting.register_matplotlib_converters()
plt.rc("figure", figsize=(10, 8))
plt.rc("font", size=10)df = pd.read_csv('https://raw.githubusercontent.com/panambY/Hourly_Energy_Consumption/master/data/PJM_Load_hourly.csv')
df.columns = ['ds', 'y']
df.insert(0, 'unique_id', 'PJM_Load_hourly')
df['ds'] = pd.to_datetime(df['ds'])
df = df.sort_values(['unique_id', 'ds']).reset_index(drop=True)
df.tail()| unique_id | ds | y | |
|---|---|---|---|
| 32891 | PJM_Load_hourly | 2001-12-31 20:00:00 | 36392.0 |
| 32892 | PJM_Load_hourly | 2001-12-31 21:00:00 | 35082.0 |
| 32893 | PJM_Load_hourly | 2001-12-31 22:00:00 | 33890.0 |
| 32894 | PJM_Load_hourly | 2001-12-31 23:00:00 | 32590.0 |
| 32895 | PJM_Load_hourly | 2002-01-01 00:00:00 | 31569.0 |
df.plot(x='ds', y='y')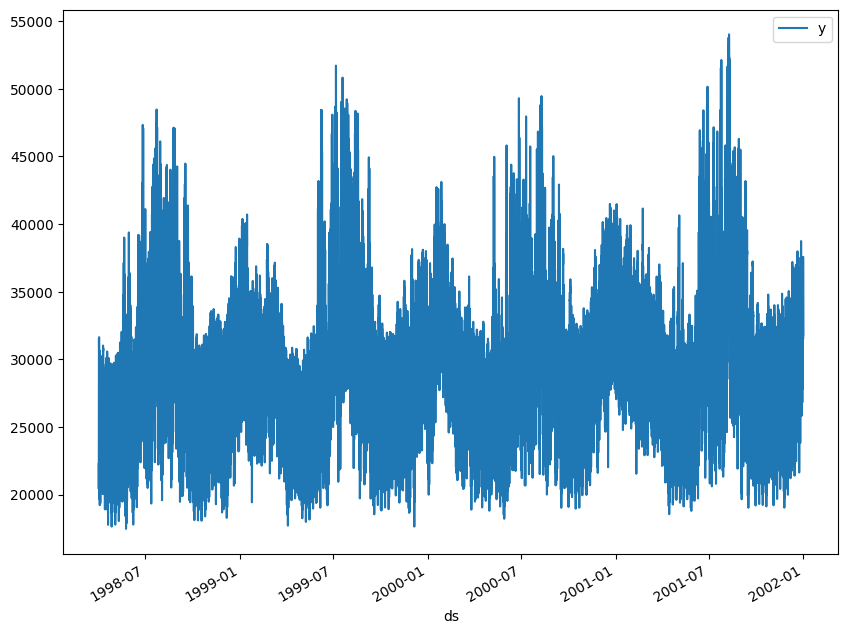
我们清楚地观察到时间序列呈现季节性模式。此外,时间序列包含32,896个观测值,因此有必要使用计算效率非常高的方法来在生产中显示它们。
MSTL模型
MSTL(使用 LOESS 的多季节性趋势分解)模型最初由 Kasun Bandara、Rob J Hyndman 和 Christoph Bergmeir 开发,它使用局部多项式回归(LOESS)将时间序列分解为多个季节性。然后,它使用自定义的非季节性模型预测趋势,并使用 SeasonalNaive 模型预测每个季节性。
StatsForecast包含了MSTL模型的快速实现。同时,可以计算时间序列的分解。
from statsforecast import StatsForecast
from statsforecast.models import MSTL, AutoARIMA, SeasonalNaive
from statsforecast.utils import AirPassengers as ap首先,我们必须定义模型参数。如前所述,电力负荷在每24小时(每小时)和每24 * 7小时(每日)内呈现季节性变化。因此,我们将使用 [24, 24 * 7] 作为MSTL模型接收的季节性。我们还必须指定预测趋势的方式。在这种情况下,我们将使用 AutoARIMA 模型。
mstl = MSTL(
season_length=[24, 24 * 7], # 时间序列的季节性
trend_forecaster=AutoARIMA() # 用于预测趋势的模型
)一旦模型被实例化,我们需要实例化 StatsForecast 类来创建预测。
sf = StatsForecast(
models=[mstl], # 用于拟合每个时间序列的模型
freq='H', # 数据的频率
)适配模型
之后,我们只需使用 fit 方法将每个模型适配到每个时间序列。
sf = sf.fit(df=df)分解具有多个季节性的时间序列
一旦模型拟合完成,我们可以通过 StatsForecast 的 fitted_ 属性访问分解结果。该属性存储了每个时间序列的拟合模型的所有相关信息。
在这种情况下,我们为单个时间序列拟合了一个模型,因此通过访问 fitted_ 位置 [0, 0],我们将找到我们模型的相关信息。MSTL 类生成了一个 model_ 属性,包含了序列分解的方式。
sf.fitted_[0, 0].model_| data | trend | seasonal24 | seasonal168 | remainder | |
|---|---|---|---|---|---|
| 0 | 22259.0 | 26183.898892 | -5215.124554 | 609.000432 | 681.225229 |
| 1 | 21244.0 | 26181.599305 | -6255.673234 | 603.823918 | 714.250011 |
| 2 | 20651.0 | 26179.294886 | -6905.329895 | 636.820423 | 740.214587 |
| 3 | 20421.0 | 26176.985472 | -7073.420118 | 615.825999 | 701.608647 |
| 4 | 20713.0 | 26174.670877 | -7062.395760 | 991.521912 | 609.202971 |
| ... | ... | ... | ... | ... | ... |
| 32891 | 36392.0 | 33123.552727 | 4387.149171 | -488.177882 | -630.524015 |
| 32892 | 35082.0 | 33148.242575 | 3479.852929 | -682.928737 | -863.166767 |
| 32893 | 33890.0 | 33172.926165 | 2307.808829 | -650.566775 | -940.168219 |
| 32894 | 32590.0 | 33197.603322 | 748.587723 | -555.177849 | -801.013195 |
| 32895 | 31569.0 | 33222.273902 | -967.124123 | -265.895357 | -420.254422 |
32896 rows × 5 columns
让我们从图形上来看一下时间序列的不同组成部分。
sf.fitted_[0, 0].model_.tail(24 * 28).plot(subplots=True, grid=True)
plt.tight_layout()
plt.show()
我们观察到有一个明显的趋势向上(橙色线)。这个成分将通过AutoARIMA模型进行预测。我们还可以观察到每24小时和每24 * 7小时都有一个非常明确的模式。这两个成分将分别使用SeasonalNaive模型进行预测。
生成预测
要生成预测,我们只需使用 predict 方法并指定预测范围 (h)。此外,为了计算与预测相关的预测区间,我们可以包含参数 level,该参数接收一个我们希望构建的预测区间水平的列表。在这种情况下,我们将仅计算90%的预测区间 (level=[90])。
forecasts = sf.predict(h=24, level=[90])
forecasts.head()| ds | MSTL | MSTL-lo-90 | MSTL-hi-90 | |
|---|---|---|---|---|
| unique_id | ||||
| PJM_Load_hourly | 2002-01-01 01:00:00 | 29956.744141 | 29585.187500 | 30328.298828 |
| PJM_Load_hourly | 2002-01-01 02:00:00 | 29057.691406 | 28407.498047 | 29707.884766 |
| PJM_Load_hourly | 2002-01-01 03:00:00 | 28654.699219 | 27767.101562 | 29542.298828 |
| PJM_Load_hourly | 2002-01-01 04:00:00 | 28499.009766 | 27407.640625 | 29590.378906 |
| PJM_Load_hourly | 2002-01-01 05:00:00 | 28821.716797 | 27552.236328 | 30091.197266 |
让我们通过图形化展示我们的预测。
_, ax = plt.subplots(1, 1, figsize = (20, 7))
df_plot = pd.concat([df, forecasts]).set_index('ds').tail(24 * 7)
df_plot[['y', 'MSTL']].plot(ax=ax, linewidth=2)
ax.fill_between(df_plot.index,
df_plot['MSTL-lo-90'],
df_plot['MSTL-hi-90'],
alpha=.35,
color='orange',
label='MSTL-level-90')
ax.set_title('PJM Load Hourly', fontsize=22)
ax.set_ylabel('Electricity Load', fontsize=20)
ax.set_xlabel('Timestamp [t]', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid()
在下一节中,我们将绘制不同的模型,因此重用之前的代码是很方便的,使用以下函数。
def plot_forecasts(y_hist, y_true, y_pred, models):
_, ax = plt.subplots(1, 1, figsize = (20, 7))
y_true = y_true.merge(y_pred, how='left', on=['unique_id', 'ds'])
df_plot = pd.concat([y_hist, y_true]).set_index('ds').tail(24 * 7)
df_plot[['y'] + models].plot(ax=ax, linewidth=2)
colors = ['orange', 'green', 'red']
for model, color in zip(models, colors):
ax.fill_between(df_plot.index,
df_plot[f'{model}-lo-90'],
df_plot[f'{model}-hi-90'],
alpha=.35,
color=color,
label=f'{model}-level-90')
ax.set_title('PJM Load Hourly', fontsize=22)
ax.set_ylabel('Electricity Load', fontsize=20)
ax.set_xlabel('Timestamp [t]', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid()MSTL模型的表现
拆分训练/测试集
为了验证 MSTL 模型的准确性,我们将展示其在未见数据上的表现。我们将使用一种经典的时间序列技术,将数据分为训练集和测试集。我们将最后 24 个观测值(最后一天)作为测试集。因此,模型将基于 32,872 个观测值进行训练。
df_test = df.tail(24)
df_train = df.drop(df_test.index)MSTL模型
除了 MSTL 模型,我们还将包括 SeasonalNaive 模型作为基准,以验证 MSTL 模型的附加价值。将 StatsForecast 模型纳入其中只需将其添加到待拟合模型的列表中。
sf = StatsForecast(
models=[mstl, SeasonalNaive(season_length=24)], # 将季节性朴素模型添加到列表中
freq='H'
)为了测量拟合时间,我们将使用time模块。
from time import time要获取测试集的预测结果,我们只需像之前一样进行拟合和预测。
init = time()
sf = sf.fit(df=df_train)
forecasts_test = sf.predict(h=len(df_test), level=[90])
end = time()
forecasts_test.head()| ds | MSTL | MSTL-lo-90 | MSTL-hi-90 | SeasonalNaive | SeasonalNaive-lo-90 | SeasonalNaive-hi-90 | |
|---|---|---|---|---|---|---|---|
| unique_id | |||||||
| PJM_Load_hourly | 2001-12-31 01:00:00 | 28345.212891 | 27973.572266 | 28716.853516 | 28326.0 | 23468.693359 | 33183.304688 |
| PJM_Load_hourly | 2001-12-31 02:00:00 | 27567.455078 | 26917.085938 | 28217.824219 | 27362.0 | 22504.693359 | 32219.306641 |
| PJM_Load_hourly | 2001-12-31 03:00:00 | 27260.001953 | 26372.138672 | 28147.865234 | 27108.0 | 22250.693359 | 31965.306641 |
| PJM_Load_hourly | 2001-12-31 04:00:00 | 27328.125000 | 26236.410156 | 28419.839844 | 26865.0 | 22007.693359 | 31722.306641 |
| PJM_Load_hourly | 2001-12-31 05:00:00 | 27640.673828 | 26370.773438 | 28910.572266 | 26808.0 | 21950.693359 | 31665.306641 |
time_mstl = (end - init) / 60
print(f'MSTL Time: {time_mstl:.2f} minutes')MSTL Time: 0.22 minutes然后我们能够生成接下来的24小时的预测。现在让我们来看一下预测值与实际值的图形比较。
plot_forecasts(df_train, df_test, forecasts_test, models=['MSTL', 'SeasonalNaive'])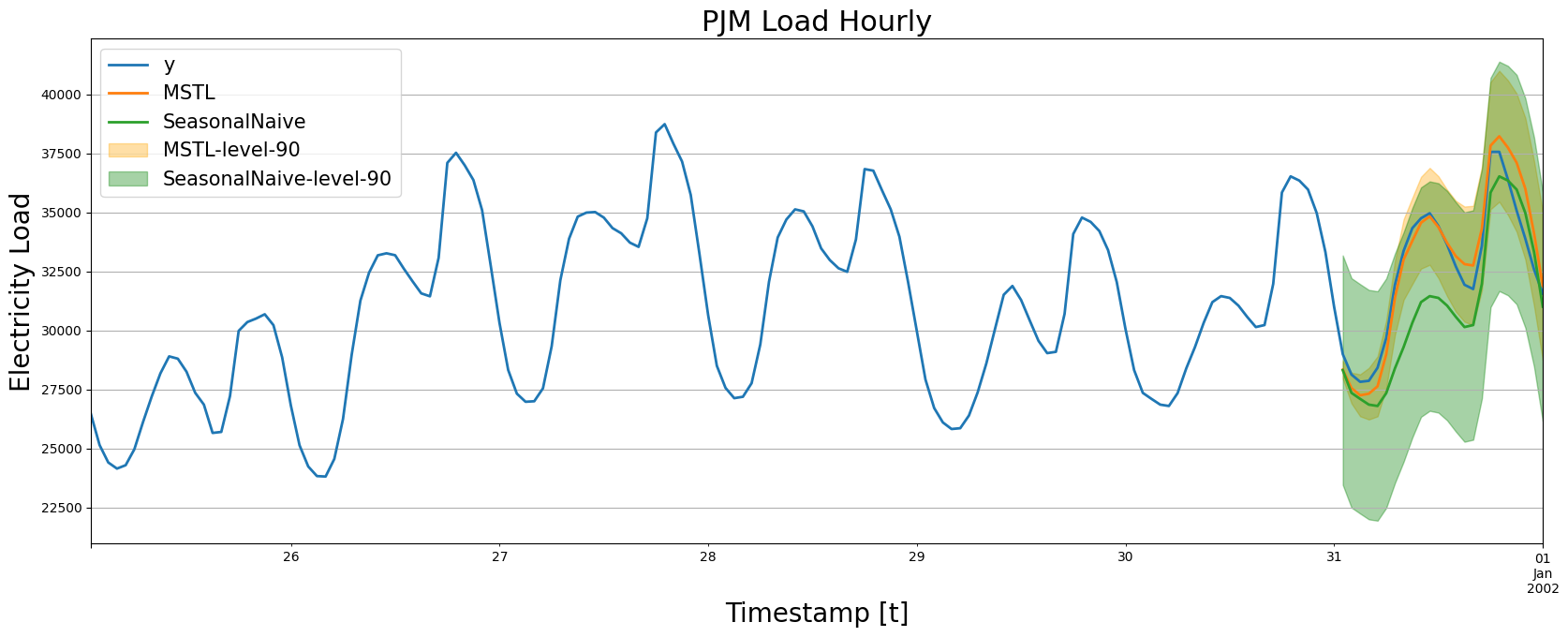
我们来看看那些仅由 MSTL 生成的内容。
plot_forecasts(df_train, df_test, forecasts_test, models=['MSTL'])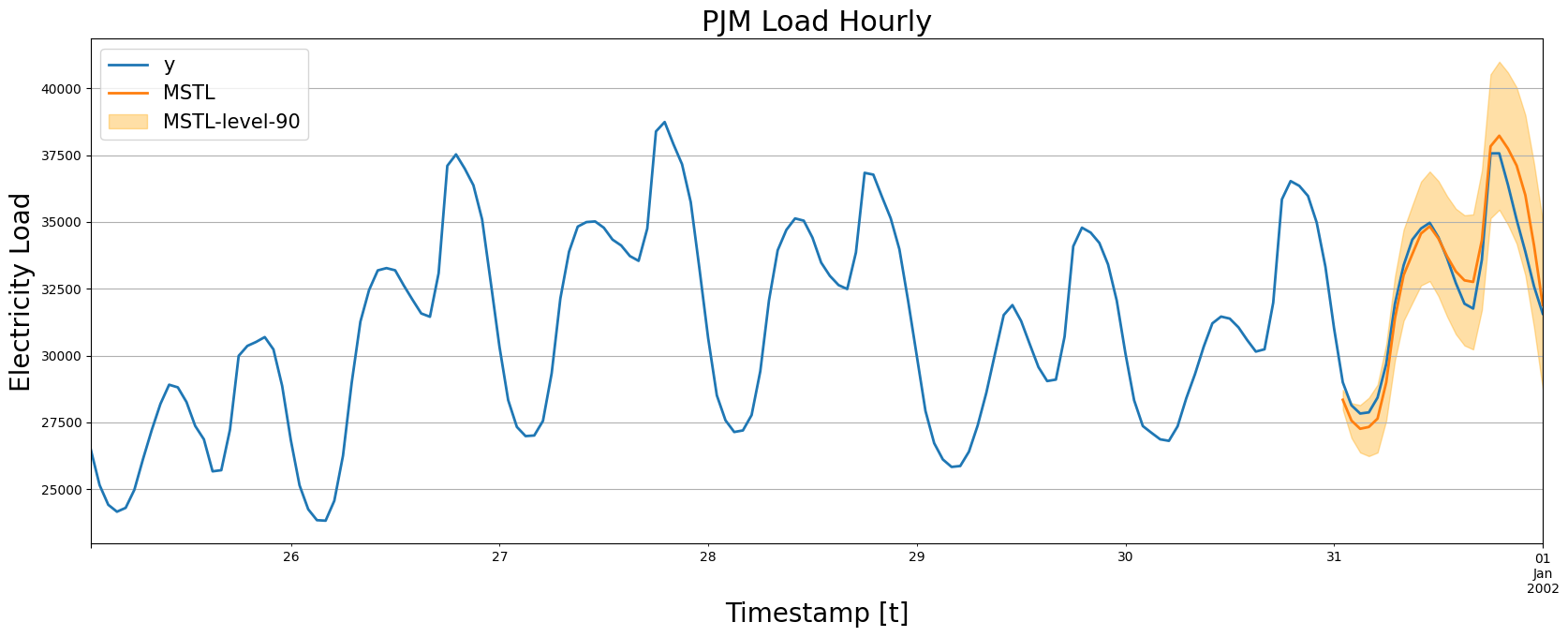
我们注意到 MSTL 产生的预测非常准确,能够跟随时间序列的行为。现在让我们数值计算模型的准确性。我们将使用以下指标:MAE、MAPE、MASE、RMSE、SMAPE。
from datasetsforecast.losses import (
mae, mape, mase, rmse, smape
)def evaluate_performace(y_hist, y_true, y_pred, models):
y_true = y_true.merge(y_pred, how='left', on=['unique_id', 'ds'])
evaluation = {}
for model in models:
evaluation[model] = {}
for metric in [mase, mae, mape, rmse, smape]:
metric_name = metric.__name__
if metric_name == 'mase':
evaluation[model][metric_name] = metric(y_true['y'].values,
y_true[model].values,
y_hist['y'].values, seasonality=24)
else:
evaluation[model][metric_name] = metric(y_true['y'].values, y_true[model].values)
return pd.DataFrame(evaluation).Tevaluate_performace(df_train, df_test, forecasts_test, models=['MSTL', 'SeasonalNaive'])| mase | mae | mape | rmse | smape | |
|---|---|---|---|---|---|
| MSTL | 0.341926 | 709.932048 | 2.182804 | 892.888012 | 2.162832 |
| SeasonalNaive | 0.894653 | 1857.541667 | 5.648190 | 2201.384101 | 5.868604 |
我们观察到,在测试集上,MSTL 相较于 SeasonalNaive 方法在 MASE 的度量上有约 60% 的改善。
与Prophet的比较
最常用的时间序列预测模型之一是 Prophet。该模型以其能够建模不同季节性(周季节性、日季节性和年季节性)而闻名。我们将使用此模型作为基准,以查看 MSTL 是否为此时间序列增值。
from prophet import Prophet
# 创建先知模型
prophet = Prophet(interval_width=0.9)
init = time()
prophet.fit(df_train)
# 生成预测
future = prophet.make_future_dataframe(periods=len(df_test), freq='H', include_history=False)
forecast_prophet = prophet.predict(future)
end = time()
# 数据整理
forecast_prophet = forecast_prophet[['ds', 'yhat', 'yhat_lower', 'yhat_upper']]
forecast_prophet.columns = ['ds', 'Prophet', 'Prophet-lo-90', 'Prophet-hi-90']
forecast_prophet.insert(0, 'unique_id', 'PJM_Load_hourly')
forecast_prophet.head()23:41:40 - cmdstanpy - INFO - Chain [1] start processing
23:41:56 - cmdstanpy - INFO - Chain [1] done processing| unique_id | ds | Prophet | Prophet-lo-90 | Prophet-hi-90 | |
|---|---|---|---|---|---|
| 0 | PJM_Load_hourly | 2001-12-31 01:00:00 | 25317.658386 | 20757.919539 | 30313.561582 |
| 1 | PJM_Load_hourly | 2001-12-31 02:00:00 | 24024.188077 | 19304.093939 | 28667.495805 |
| 2 | PJM_Load_hourly | 2001-12-31 03:00:00 | 23348.306824 | 18608.982825 | 28497.334752 |
| 3 | PJM_Load_hourly | 2001-12-31 04:00:00 | 23356.150113 | 18721.142270 | 28136.888630 |
| 4 | PJM_Load_hourly | 2001-12-31 05:00:00 | 24130.861217 | 19896.188455 | 28970.202276 |
time_prophet = (end - init) / 60
print(f'Prophet Time: {time_prophet:.2f} minutes')Prophet Time: 0.30 minutestimes = pd.DataFrame({'model': ['MSTL', 'Prophet'], 'time (mins)': [time_mstl, time_prophet]})
times| model | time (mins) | |
|---|---|---|
| 0 | MSTL | 0.217266 |
| 1 | Prophet | 0.301172 |
我们观察到,Prophet 执行拟合和预测流程所需的时间大于 MSTL。让我们来看看 Prophet 生成的预测结果。
forecasts_test = forecasts_test.merge(forecast_prophet, how='left', on=['unique_id', 'ds'])plot_forecasts(df_train, df_test, forecasts_test, models=['MSTL', 'SeasonalNaive', 'Prophet'])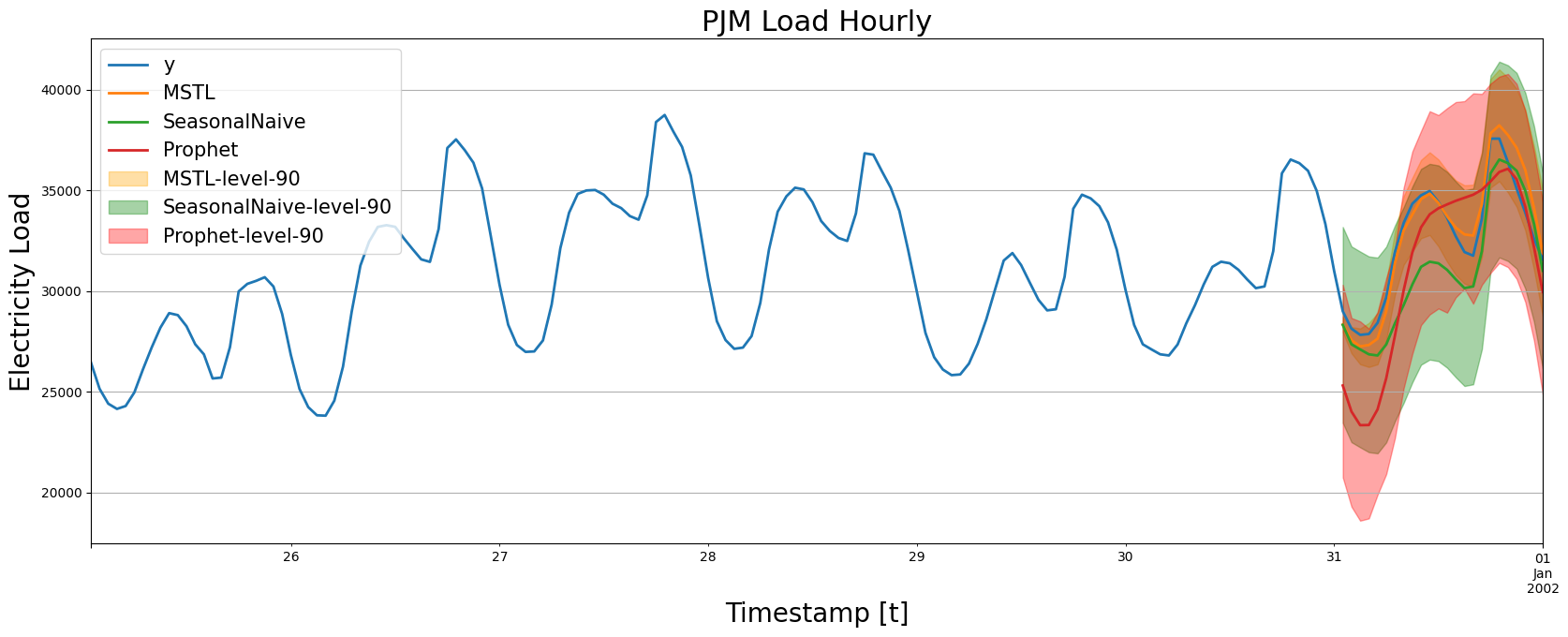
我们注意到 Prophet 能够捕捉时间序列的整体行为。然而,在某些情况下,它的预测值远低于实际值。它也无法正确调整谷底。
evaluate_performace(df_train, df_test, forecasts_test, models=['MSTL', 'Prophet', 'SeasonalNaive'])| mase | mae | mape | rmse | smape | |
|---|---|---|---|---|---|
| MSTL | 0.341926 | 709.932048 | 2.182804 | 892.888012 | 2.162832 |
| Prophet | 1.094768 | 2273.036373 | 7.343292 | 2709.400341 | 7.688665 |
| SeasonalNaive | 0.894653 | 1857.541667 | 5.648190 | 2201.384101 | 5.868604 |
就准确性而言,Prophet无法产生比SeasonalNaive模型更好的预测,然而,MSTL模型使得Prophet的预测提高了69%(MASE)。
与NeuralProphet的比较
NeuralProphet 是使用深度学习的 Prophet 版本。该模型还能够处理不同的季节性,因此我们也将其用作基准。
from neuralprophet import NeuralProphet
neuralprophet = NeuralProphet(quantiles=[0.05, 0.95])
init = time()
neuralprophet.fit(df_train.drop(columns='unique_id'))
future = neuralprophet.make_future_dataframe(df=df_train.drop(columns='unique_id'), periods=len(df_test))
forecast_np = neuralprophet.predict(future)
end = time()
forecast_np = forecast_np[['ds', 'yhat1', 'yhat1 5.0%', 'yhat1 95.0%']]
forecast_np.columns = ['ds', 'NeuralProphet', 'NeuralProphet-lo-90', 'NeuralProphet-hi-90']
forecast_np.insert(0, 'unique_id', 'PJM_Load_hourly')
forecast_np.head()WARNING - (NP.forecaster.fit) - When Global modeling with local normalization, metrics are displayed in normalized scale.
INFO - (NP.df_utils._infer_frequency) - Major frequency H corresponds to 99.973% of the data.
INFO - (NP.df_utils._infer_frequency) - Dataframe freq automatically defined as H
INFO - (NP.config.init_data_params) - Setting normalization to global as only one dataframe provided for training.
INFO - (NP.config.set_auto_batch_epoch) - Auto-set batch_size to 64
INFO - (NP.config.set_auto_batch_epoch) - Auto-set epochs to 76INFO - (NP.df_utils._infer_frequency) - Major frequency H corresponds to 99.973% of the data.
INFO - (NP.df_utils._infer_frequency) - Defined frequency is equal to major frequency - H
INFO - (NP.df_utils.return_df_in_original_format) - Returning df with no ID column
INFO - (NP.df_utils._infer_frequency) - Major frequency H corresponds to 95.833% of the data.
INFO - (NP.df_utils._infer_frequency) - Defined frequency is equal to major frequency - H
INFO - (NP.df_utils._infer_frequency) - Major frequency H corresponds to 95.833% of the data.
INFO - (NP.df_utils._infer_frequency) - Defined frequency is equal to major frequency - HINFO - (NP.df_utils.return_df_in_original_format) - Returning df with no ID column| unique_id | ds | NeuralProphet | NeuralProphet-lo-90 | NeuralProphet-hi-90 | |
|---|---|---|---|---|---|
| 0 | PJM_Load_hourly | 2001-12-31 01:00:00 | 25019.892578 | 22296.675781 | 27408.724609 |
| 1 | PJM_Load_hourly | 2001-12-31 02:00:00 | 24128.816406 | 21439.851562 | 26551.615234 |
| 2 | PJM_Load_hourly | 2001-12-31 03:00:00 | 23736.679688 | 20961.978516 | 26289.349609 |
| 3 | PJM_Load_hourly | 2001-12-31 04:00:00 | 23476.744141 | 20731.619141 | 26050.443359 |
| 4 | PJM_Load_hourly | 2001-12-31 05:00:00 | 23899.162109 | 21217.503906 | 26449.603516 |
time_np = (end - init) / 60
print(f'Prophet Time: {time_np:.2f} minutes')Prophet Time: 2.95 minutestimes = times.append({'model': 'NeuralProphet', 'time (mins)': time_np}, ignore_index=True)
times| model | time (mins) | |
|---|---|---|
| 0 | MSTL | 0.217266 |
| 1 | Prophet | 0.301172 |
| 2 | NeuralProphet | 2.946358 |
我们观察到NeuralProphet所需的处理时间比Prophet和MSTL更长。
forecasts_test = forecasts_test.merge(forecast_np, how='left', on=['unique_id', 'ds'])plot_forecasts(df_train, df_test, forecasts_test, models=['MSTL', 'NeuralProphet', 'Prophet'])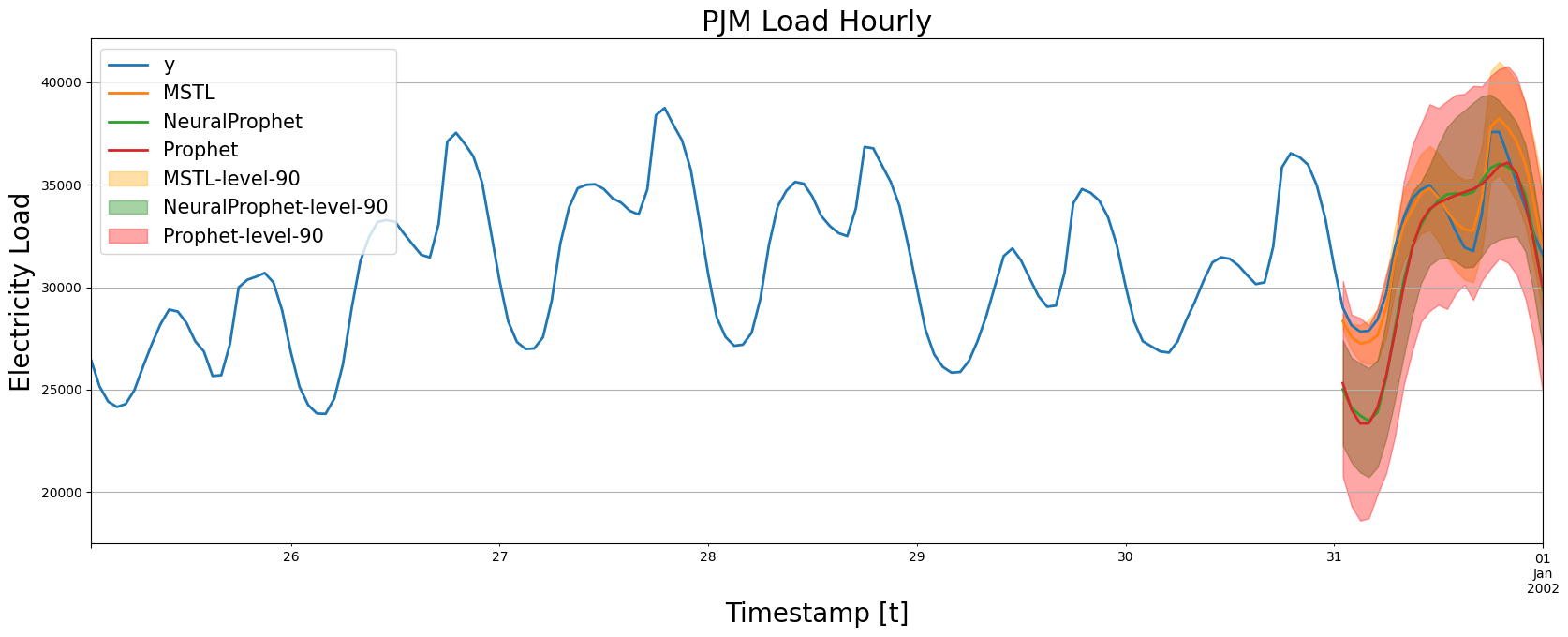
预测图表显示,NeuralProphet 生成的结果与 Prophet 非常相似,正如预期的那样。
evaluate_performace(df_train, df_test, forecasts_test, models=['MSTL', 'NeuralProphet', 'Prophet', 'SeasonalNaive'])| mase | mae | mape | rmse | smape | |
|---|---|---|---|---|---|
| MSTL | 0.341926 | 709.932048 | 2.182804 | 892.888012 | 2.162832 |
| NeuralProphet | 1.084915 | 2252.578613 | 7.280202 | 2671.145730 | 7.615492 |
| Prophet | 1.094768 | 2273.036373 | 7.343292 | 2709.400341 | 7.688665 |
| SeasonalNaive | 0.894653 | 1857.541667 | 5.648190 | 2201.384101 | 5.868604 |
在数值评估方面,NeuralProphet 的结果相对于 Prophet 有所提升,这在预期之中。然而,MSTL 的预测结果相比于 NeuralProphet 提升了68%(MASE)。
NeuralProphet 的性能可以通过超参数优化来提高,这会显著增加拟合时间。在这个例子中,我们展示了默认版本的性能。
结论
在这篇文章中,我们介绍了 MSTL,这是一个由 Kasun Bandara, Rob Hyndman 和 Christoph Bergmeir 原创开发的模型,能够处理具有多重季节性的时间序列。我们还展示了对于PJM电力负荷时间序列,相比于 Prophet 和 NeuralProphet 模型,MSTL 在时间和准确率上提供了更好的性能。
参考文献
Give us a ⭐ on Github