AutoETS 模型


# 此单元格将不会被渲染，但用于隐藏警告并限制显示的行数。

import warnings
warnings.filterwarnings("ignore")

import logging
logging.getLogger('statsforecast').setLevel(logging.ERROR)

import pandas as pd
pd.set_option('display.max_rows', 6)

使用 Statsforecast 的 AutoETS 模型 的逐步指南。

在本教程中，我们将熟悉主要的 StatsForecast 类以及一些相关的方法，例如 StatsForecast.plot、StatsForecast.forecast 和 StatsForecast.cross_validation 等。

介绍

在商业中，往往需要对大量单变量时间序列进行自动预测。通常，需要对超过一千种产品线进行至少每月一次的预测。即使在需要较少预测的情况下，可能也没有合适的人员经过适当培训来使用时间序列模型进行预测。在这些情况下，自动预测算法是一个必不可少的工具。自动预测算法必须确定一个合适的时间序列模型，估计参数并计算预测值。它们必须能够抵御异常的时间序列模式，并适用于大量序列而无需用户干预。最流行的自动预测算法基于指数平滑或ARIMA模型。

指数平滑

尽管指数平滑方法自1950年代以来就已存在，但结合模型选择程序的建模框架直到最近才得以发展。Ord, Koehler 和 Snyder (1997)，Hyndman, Koehler, Snyder, 和 Grose (2002) 以及 Hyndman, Koehler, Ord 和 Snyder (2005b) 已经证明，所有指数平滑方法（包括非线性方法）都是来自创新状态空间模型的最优预测。

指数平滑方法最初根据 Pegels’ (1969) 的分类法进行分类。此后，Gardner (1985) 拓展了这一分类，Hyndman et al. (2002) 对其进行了修改，Taylor (2003) 再次进行了扩展，共有十五种方法如下面的表所示。

趋势成分	季节成分

成分	N（无）	A（加性）	M（乘性）
N（无）	(N,N)	(N,A)	(N,M)
A（加性）	(A,N)	(A,A)	(A,M)
Ad（加性衰减）	(Ad,N)	(Ad,A)	(Ad,M)
M（乘性）	(M,N )	(M,A )	(M,M)
Md（乘性衰减）	(Md,N )	( Md,A)	(Md,M)

其中一些方法在其他名称下更为人知。例如，单元 (N,N) 描述了 简单指数平滑（或 SES）方法，单元 (A,N) 描述了 霍尔特线性方法，而单元 (Ad,N) 描述了 衰减趋势方法。加性霍尔特-温特斯方法由单元 (A,A) 给出，乘性霍尔特-温特斯方法由单元 (A,M) 给出。其他单元对应于使用较少但类似的方法。

所有方法的点预测

我们用 $y_1,y_2,...,y_n$ 表示观测时间序列。基于到时间 $t$ 的所有数据对 $y_{t+h}$ 的预测用 $\hat y_{t+h|t}$ 表示。为了说明该方法，我们给出方法 (A,A)，即 Holt-Winters 加法方法的点预测和更新方程：

\[\begin{align*} 水平: \ell_{t} &= \alpha(y_{t} - s_{t-m}) + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \tag{1a} \\ 增长: b_{t} &= \beta^*(\ell_{t} - \ell_{t-1}) + (1 - \beta^*)b_{t-1} \tag{1b} \\ 季节性: s_{t} &= \gamma (y_{t}-\ell_{t-1}-b_{t-1}) + (1-\gamma)s_{t-m},\tag{1c} \\ 预测:\hat{y}_{t+h|t} &= \ell_{t} + hb_{t} + s_{t+h-m(k+1)} \tag{1d} \\ \end{align*}\]

其中 $m$ 是季节长度（例如，一年中的月份或季度数），$\ell_{t}$ 代表序列的水平，$b_t$ 表示增长，$s_t$ 是季节性成分，$\hat y_{t+h|t}$ 是对 $h$ 周期前的预测，$h_{m}^{+} = [(h − 1) mod \ m] + 1$。要使用方法 (1)，我们需要初始状态 $\ell_{0}$、$b_0$ 和 $s_{1−m}, . . . , s_0$ 的取值，以及平滑参数 $\alpha, \beta^{*}$ 和 $\gamma$。所有这些都将从观察数据中估计得出。

方程 (1c) 与 Makridakis 等人（1998）或 Bowerman, O’Connell 和 Koehler（2005）中的常规 Holt-Winters 方程略有不同。这些作者用以下方程替换 (1c)： \[s_{t} = \gamma^* (y_{t}-\ell_{t})+ (1-\gamma^*)s_{t-m}.\]

如果使用 (1a) 替代 $\ell_{t}$，我们得到

\[s_{t} = \gamma^*(1-\alpha) (y_{t}-\ell_{t-1}-b_{t-1})+ [1-\gamma^*(1-\alpha)]s_{t-m},\]

因此，通过将公式 (1c) 中的 $\gamma$ 替换为 $\gamma^{*} (1-\alpha)$，我们可以获得相同的预测。Ord 等人（1997）提出的 (1c) 的修改使状态空间形式更简单。它等同于 Archibald（1990）对 Holt-Winters 方法的变体。

创新状态空间模型

对于其他ETS模型中的每种指数平滑方法，Hyndman等人（2008b）描述了两种可能的创新状态空间模型，一种对应于加性误差模型，另一种对应于乘性误差模型。如果使用相同的参数值，这两个模型会给出等效的点预测，尽管预测区间不同。因此，在这个分类中描述了30个潜在模型。

从历史上看，误差成分的性质常常被忽视，因为加性和乘性误差之间的区别对点预测没有影响。

我们谨慎地区分指数平滑方法和基础状态空间模型。指数平滑方法是一种仅用于生成点预测的算法。基础随机状态空间模型给出相同的点预测，但也提供了计算预测区间和其他性质的框架。

为了区分加性和乘性误差的模型，我们在方法符号的前面添加一个额外的字母。三元组 (E,T,S) 指的是三个组成部分：误差、趋势和季节性。因此，模型 ETS(A,A,N) 具有加性误差、加性趋势且没有季节性——换句话说，这就是Holt的线性方法与加性误差。类似地，ETS(M,Md,M) 指的是具有乘性误差、阻尼乘性趋势和乘性季节性的模型。符号 ETS(·,·,·) 有助于记住各个组件被指定的顺序。

一旦指定了模型，我们可以研究系列未来值的概率分布，并找到例如，给定过去信息的未来观测值的条件均值。我们将其表示为 $\mu_{t+h|t} = E(y_{t+h | xt})$，其中 xt 包含未观察到的组件，如 $\ell_t$、$b_t$ 和 $s_t$。对于 $h = 1$，我们使用 $\mu_t ≡ \mu_{t+1|t}$ 作为简写符号。对于许多模型，这些条件均值将与表中给出的点预测相同其他ETS模型，从而 $ {t+h|t} = y{t+h|t} $。然而，对于其他模型（那些具有乘性趋势或乘性季节性的），条件均值和点预测在 $h ≥ 2$ 时会有所不同。

我们使用Gardner和McKenzie（1985）的阻尼趋势方法来说明这些思想。

每个模型由一个测量方程组成，该方程描述了观察到的数据，以及一些状态方程，描述未观察到的成分或状态（水平、趋势、季节）如何随时间变化。因此，这些被称为状态空间模型。

对于每种方法，存在两种模型：一种是带有加性误差的，另一种是带有乘性误差的。如果使用相同的平滑参数值，则由模型生成的点预测是相同的。然而，它们将生成不同的预测区间。

为了区分带有加性误差的模型和带有乘性误差的模型（同时也区分这些模型与方法），我们在上述表格的分类中添加了第三个字母。我们将每个状态空间模型标记为 ETS(⋅,.,.)，表示（误差、趋势、季节）。这个标签也可以看作是指数平滑。使用与上述表格相同的符号，每个组件（或状态）的可能性为：误差 = { A,M }，趋势 = {N,A,Ad}，季节 = { N,A,M }。

ETS(A,N,N)：带有加性误差的简单指数平滑

回顾简单指数平滑的分量形式：

\[\begin{align*} \text{预测方程} && \hat{y}_{t+1|t} & = \ell_{t}\\ \text{平滑方程} && \ell_{t} & = \alpha y_{t} + (1 - \alpha)\ell_{t-1}. \end{align*}\]

如果我们重新排列水平的平滑方程，我们得到“误差修正”形式，

\[\begin{align*} \ell_{t} %&= \alpha y_{t}+\ell_{t-1}-\alpha\ell_{t-1}\\ &= \ell_{t-1}+\alpha( y_{t}-\ell_{t-1})\\ &= \ell_{t-1}+\alpha e_{t}, \end{align*}\]

其中 $e_{t}=y_{t}-\ell_{t-1}=y_{t}-\hat{y}_{t|t-1}$ 是时间 $t$ 的残差。

训练数据的误差导致在平滑过程中对估计水平的调整，适用于 $t=1,\dots,T$。例如，如果时间 $t$ 的误差为负，则 $y_t < \hat{y}_{t|t-1}$，因此时间 $t-1$ 的水平被高估。新的水平 $\ell_{t}$ 是之前水平 $\ell_{t-1}$ 向下调整后的结果。$\alpha$ 越接近于1，水平的估计就越“粗糙”（发生较大调整）。$\alpha$ 越小，水平就越“平滑”（发生较小调整）。

我们还可以写作 $y_t = \ell_{t-1} + e_t$，这样每个观测值可以表示为前一个水平加上一个误差。为了将其转化为创新状态空间模型，我们只需指定 $e_t$ 的概率分布。对于具有加性误差的模型，我们假设残差（一步训练误差）$e_t$ 服从均值为0、方差为$\sigma^2$ 的正态分布白噪声。对此的简便记法为 $e_t = \varepsilon_t\sim\text{NID}(0,\sigma^2)$；NID 代表“正态独立分布”。

然后模型的方程可以写成

\[\begin{align} y_t &= \ell_{t-1} + \varepsilon_t \tag{2}\\ \ell_t&=\ell_{t-1}+\alpha \varepsilon_t. \tag{3} \end{align}\]

我们将 (2) 称为测量（或观测）方程，(3) 称为状态（或转移）方程。这两个方程，加上误差的统计分布，形成一个完全指定的统计模型。具体而言，这些构成了简单指数平滑的创新状态空间模型。

“创新”一词来源于所有方程使用同一个随机误差过程 $\varepsilon_t$。出于同样的原因，这种表述也被称为“单一误差源”模型。还有其他多重误差源的表述，在这里我们不做介绍。

测量方程显示了观测值与未观察状态之间的关系。在这种情况下，观测值 $y_t$ 是水平 $\ell_{t-1}$ 的线性函数，$y_t$ 的可预测部分，以及误差 $\varepsilon_t$，$y_t$ 的不可预测部分。对于其他创新状态空间模型，这种关系可能是非线性的。

状态方程显示了状态随时间的演变。平滑参数 $\alpha$ 的影响与之前讨论的方法相同。例如，$\alpha$ 控制连续水平的变化量：高值的 $\alpha$ 允许快速变化；低值的 $\alpha$ 导致平滑变化。如果 $\alpha=0$，系列的水平随时间不变；如果 $\alpha=1$，模型简化为随机游走模型 $y_t=y_{t-1}+\varepsilon_t$。

ETS(M,N,N): 简单指数平滑与乘法误差

以类似的方式，我们可以通过将一步预测训练误差写为相对误差来指定具有乘法误差的模型

\[\varepsilon_t = \frac{y_t-\hat{y}_{t|t-1}}{\hat{y}_{t|t-1}}\]

其中 $\varepsilon_t \sim \text{NID}(0,\sigma^2)$。将 $\hat{y}_{t|t-1}=\ell_{t-1}$ 代入得到 $y_t = \ell_{t-1}+\ell_{t-1}\varepsilon_t$ 和 $e_t = y_t - \hat{y}_{t|t-1} = \ell_{t-1}\varepsilon_t$。

然后我们可以将状态空间模型的乘法形式写成

\[\begin{align*} y_t&=\ell_{t-1}(1+\varepsilon_t)\\ \ell_t&=\ell_{t-1}(1+\alpha \varepsilon_t). \end{align*}\]

ETS(A,A,N): 霍尔特线性方法与加法误差

对于此模型，我们假设一步预测的训练误差由以下公式给出

\[\varepsilon_t=y_t-\ell_{t-1}-b_{t-1} \sim \text{NID}(0,\sigma^2)\]

将其代入霍尔特线性方法的误差修正方程中，我们得到

\[\begin{align*} y_t&=\ell_{t-1}+b_{t-1}+\varepsilon_t\\ \ell_t&=\ell_{t-1}+b_{t-1}+\alpha \varepsilon_t\\ b_t&=b_{t-1}+\beta \varepsilon_t, \end{align*}\]

其中为简化起见，我们设定 $\beta=\alpha \beta^*$。

ETS(M,A,N): 霍尔特线性法与乘法误差

指定一步预测的训练误差为相对误差，因此

\[\varepsilon_t=\frac{y_t-(\ell_{t-1}+b_{t-1})}{(\ell_{t-1}+b_{t-1})}\]

遵循与上述相似的方法，霍尔特线性法下的乘法误差的创新状态空间模型被指定为

\[\begin{align*} y_t&=(\ell_{t-1}+b_{t-1})(1+\varepsilon_t)\\ \ell_t&=(\ell_{t-1}+b_{t-1})(1+\alpha \varepsilon_t)\\ b_t&=b_{t-1}+\beta(\ell_{t-1}+b_{t-1}) \varepsilon_t, \end{align*}\]

其中 $\beta=\alpha \beta^*$ 并且 $\varepsilon_t \sim \text{NID}(0,\sigma^2)$。

估计ETS模型

通过最小化平方误差之和来估计参数的一个替代方法是最大化“似然”。似然是数据来源于指定模型的概率。因此，较大的似然与良好的模型相关联。对于加法误差模型，最大化似然（假设误差服从正态分布）与最小化平方误差之和给出相同的结果。然而，对于乘法误差模型，会得到不同的结果。在本节中，我们将通过最大化似然来估计平滑参数 $\alpha, \beta, \gamma$ 和 $\phi$ 以及初始状态 $\ell_0, b_0, s_0, s_{-1}, \dots, s_{-m+1}$。

平滑参数可以取的可能值是有限制的。传统上，这些参数被限制在0和1之间，以便这些方程可以被解释为加权平均数。也就是说，$0< \alpha,\beta^*,\gamma^*,\phi<1$。对于状态空间模型，我们设置 $\beta=\alpha\beta^*$ 和 $\gamma=(1-\alpha)\gamma^*$. 因此，传统限制转化为 $0< \alpha <1, 0 < \beta < \alpha$ 和 $0< \gamma < 1-\alpha$。实际上，阻尼参数 $\phi$ 通常被进一步约束，以防止在估计模型时出现数值困难。

另一个看待这些参数的方法是考虑状态空间模型的数学性质。这些参数受到约束，以防止远古观察对当前预测持续产生影响。这导致对参数的一些可接受性约束，这些约束通常（但并不总是）比传统约束区域更不严格 (Hyndman et al., 2008, pp. 149-161)。例如，对于 ETS(A,N,N) 模型，传统参数区域是 $0< \alpha <1$，但可接受区域是 $0< \alpha <2$。对于 ETS(A,A,N) 模型，传统参数区域是 $0<\alpha<1$ 和 $0<\beta<\alpha$，但可接受区域是 $0<\alpha<2$ 和 $0<\beta<4-2\alpha$。

模型选择

ETS 统计框架的一个重大优势是可以使用信息准则进行模型选择。AIC, AIC_c 和 BIC 可以用来确定哪种 ETS 模型最适合给定的时间序列。

对于 ETS 模型，赤池信息量准则 (AIC) 定义为

\[\text{AIC} = -2\log(L) + 2k,\]

其中 $L$ 是模型的似然性，$k$ 是已估计的参数和初始状态的总数（包括残差方差）。

修正小样本偏差的 AIC (AIC_c) 定义为

\[AIC_c = AIC + \frac{2k(k+1)}{T-k-1}\]

而贝叶斯信息准则 (BIC) 为

\[\text{BIC} = \text{AIC} + k[\log(T)-2]\]

三种 (误差, 趋势, 季节) 的组合可能会导致数值问题。具体而言，可能导致这种不稳定性的模型是 ETS(A,N,M), ETS(A,A,M) 和 ETS(A,Ad,M)，这是由于状态方程中可能接近零的值造成的除法。在选择模型时，我们通常不考虑这些特定的组合。

当数据严格为正时，乘法误差模型是有用的，但如果数据包含零或负值，计算上就不稳定。因此，如果时间序列不是严格正数，则不会考虑乘法误差模型。在这种情况下，只会采用六种完全加性的模型。

加载库和数据

Tip

需要使用Statsforecast。要安装，请参阅安装说明。

接下来，我们导入绘图库并配置绘图样式。

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf

plt.style.use('fivethirtyeight')
plt.rcParams['lines.linewidth'] = 1.5
dark_style = {
    'figure.facecolor': '#212946',
    'axes.facecolor': '#212946',
    'savefig.facecolor':'#212946',
    'axes.grid': True,
    'axes.grid.which': 'both',
    'axes.spines.left': False,
    'axes.spines.right': False,
    'axes.spines.top': False,
    'axes.spines.bottom': False,
    'grid.color': '#2A3459',
    'grid.linewidth': '1',
    'text.color': '0.9',
    'axes.labelcolor': '0.9',
    'xtick.color': '0.9',
    'ytick.color': '0.9',
    'font.size': 12 }
plt.rcParams.update(dark_style)

from pylab import rcParams
rcParams['figure.figsize'] = (18,7)

读取数据

df = pd.read_csv("https://raw.githubusercontent.com/Naren8520/Serie-de-tiempo-con-Machine-Learning/main/Data/Esperanza_vida.csv", usecols=[1,2])
df.head()

	year	value
0	1960-01-01	69.123902
1	1961-01-01	69.760244
2	1962-01-01	69.149756
3	1963-01-01	69.248049
4	1964-01-01	70.311707

StatsForecast 的输入总是一个具有三列的长格式数据框：unique_id、ds 和 y：

unique_id（字符串、整数或类别）表示序列的标识符。
ds（日期戳）列应为 Pandas 预期的格式，理想情况下为 YYYY-MM-DD 表示日期或 YYYY-MM-DD HH:MM:SS 表示时间戳。
y（数值）表示我们希望进行预测的测量值。

df["unique_id"]="1"
df.columns=["ds", "y", "unique_id"]
df.head()

	ds	y	unique_id
0	1960-01-01	69.123902	1
1	1961-01-01	69.760244	1
2	1962-01-01	69.149756	1
3	1963-01-01	69.248049	1
4	1964-01-01	70.311707	1

print(df.dtypes)

ds            object
y            float64
unique_id     object
dtype: object

我们需要将 ds 从 object 类型转换为 datetime。

df["ds"] = pd.to_datetime(df["ds"])

使用 plot 方法探索数据

使用 StatsForecast 类中的 plot 方法绘制一些系列。此方法从数据集中打印随机系列，适用于基本的 EDA。

from statsforecast import StatsForecast

StatsForecast.plot(df)

自相关图

fig, axs = plt.subplots(nrows=1, ncols=2)

plot_acf(df["y"],  lags=20, ax=axs[0],color="fuchsia")
axs[0].set_title("Autocorrelation");

# 情节
plot_pacf(df["y"],  lags=20, ax=axs[1],color="lime")
axs[1].set_title('Partial Autocorrelation')

plt.show();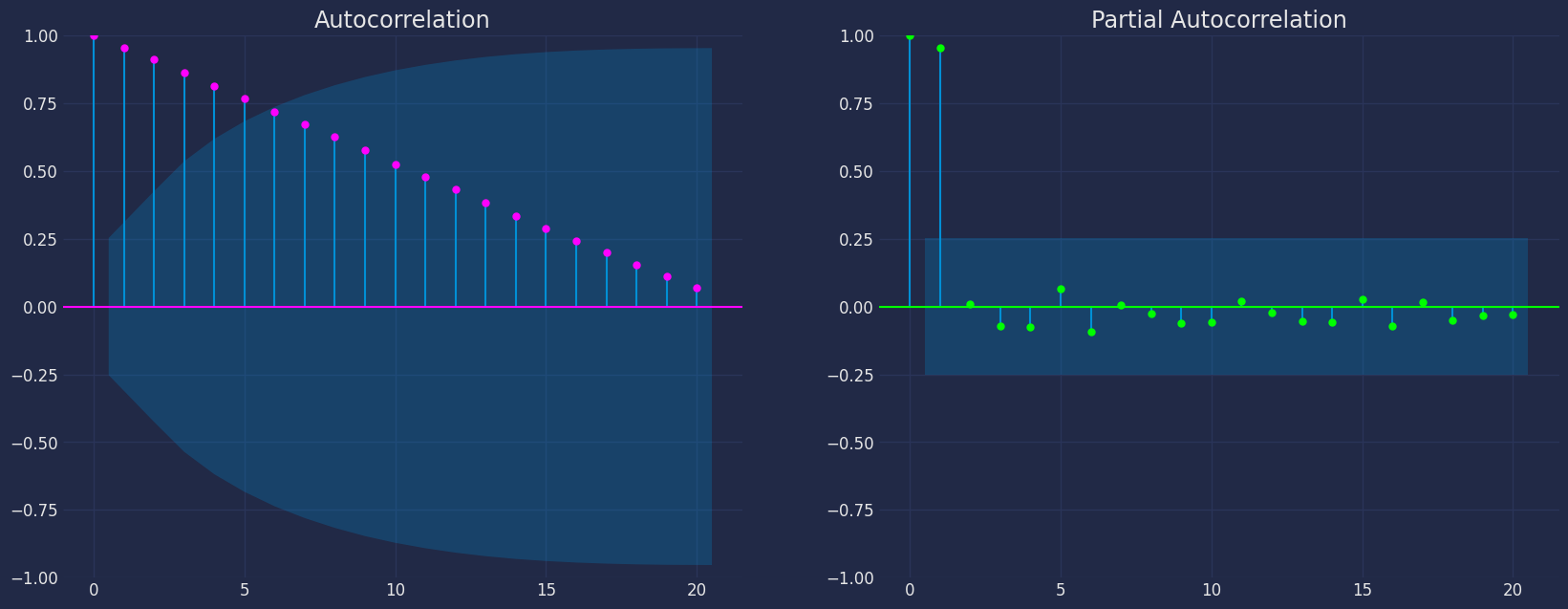

时间序列的分解

如何分解时间序列以及原因？

在时间序列分析中，为了预测新值，了解过去的数据是非常重要的。更正式地说，了解值随时间变化所遵循的模式是非常重要的。导致我们的预测值偏离正确方向的原因可以有很多。基本上，时间序列由四个组成部分构成。这些组成部分的变动导致时间序列模式的变化。这些组成部分是：

水平（Level）： 这是随着时间平均值的主要值。
趋势（Trend）： 趋势是导致时间序列中增加或减少模式的值。
季节性（Seasonality）： 这是在短时间内发生的周期性事件，会导致时间序列中短期的增长或减少模式。
残差/噪声（Residual/Noise）： 这些是时间序列中的随机变化。

这些组成部分随时间的结合导致了时间序列的形成。大多数时间序列由水平和噪声/残差组成，趋势或季节性则是可选值。

如果季节性和趋势是时间序列的一部分，则会对预测值产生影响，因为预测时间序列的模式可能与之前的时间序列不同。

时间序列中组成部分的组合可以分为两种类型： * 加性（Additive） * 乘性（Multiplicative）

加性时间序列

如果时间序列的组成部分是相加而成，则这个时间序列被称为加性时间序列。通过可视化，我们可以说，如果时间序列的增加或减少模式在整个序列中是相似的，那么时间序列是加性的。任何加性时间序列的数学函数可以表示为： \[y(t) = 水平 + 趋势 + 季节性 + 噪声\]

乘性时间序列

如果时间序列的组成部分是相乘而成，则这个时间序列被称为乘性时间序列。通过可视化，如果时间序列随着时间的推移呈现指数增长或下降，则可以将此时间序列视为乘性时间序列。乘性时间序列的数学函数可以表示为： \[y(t) = 水平 * 趋势 * 季节性 * 噪声\]

from statsmodels.tsa.seasonal import seasonal_decompose 
a = seasonal_decompose(df["y"], model = "add", period=1)
a.plot();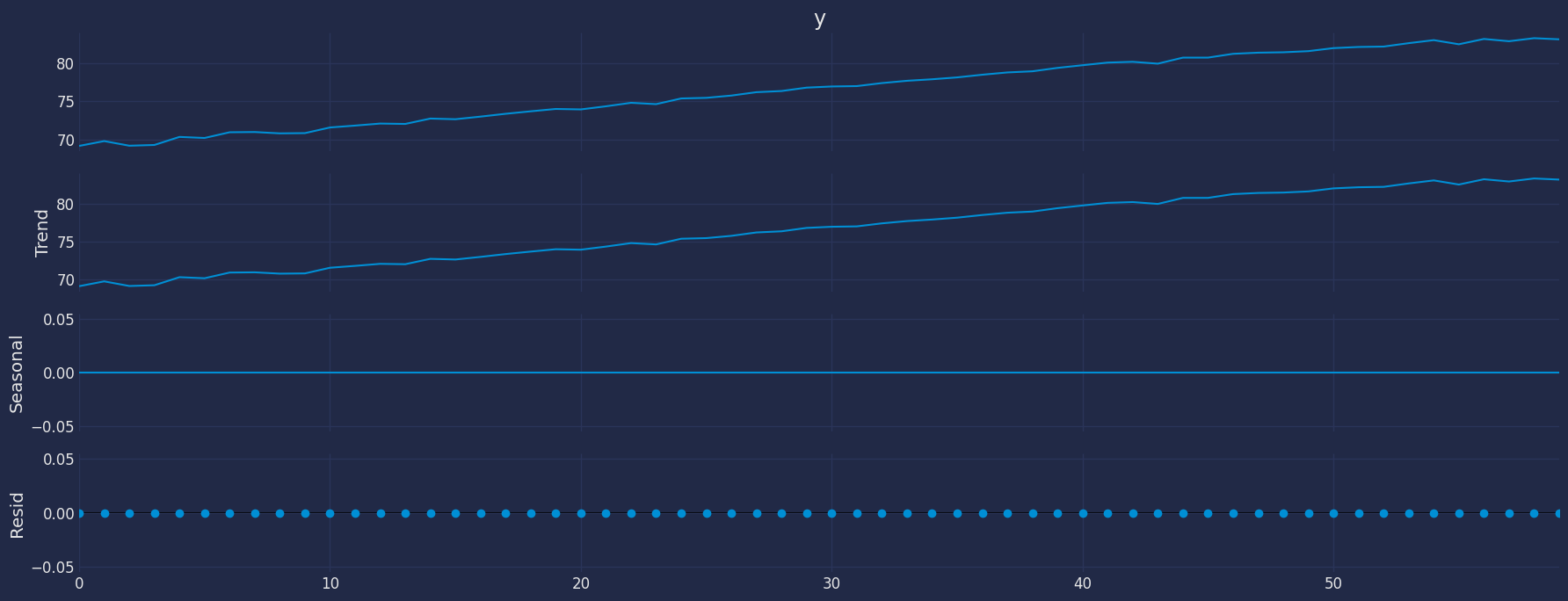

将时间序列分解为其组成部分有助于我们识别所分析时间序列的行为。此外，这还有助于我们了解可以应用哪种类型的模型。例如，在生命期望数据集中，我们可以观察到我们的时间序列在全年表现出上升趋势，另一方面，也可以观察到该时间序列没有季节性。

通过查看之前的图表并了解每个组成部分，我们可以对可以应用的模型有所了解： * 我们有趋势 * 没有季节性

将数据分为训练集和测试集

让我们将数据划分为几个集合

用于训练我们模型的数据。
用于测试我们模型的数据。

对于测试数据，我们将使用最后6年的数据来测试和评估我们模型的性能。

train = df[df.ds<='2013-01-01'] 
test = df[df.ds>'2013-01-01']

train.shape, test.shape

((54, 3), (6, 3))

sns.lineplot(train,x="ds", y="y", label="Train")
sns.lineplot(test, x="ds", y="y", label="Test")
plt.show()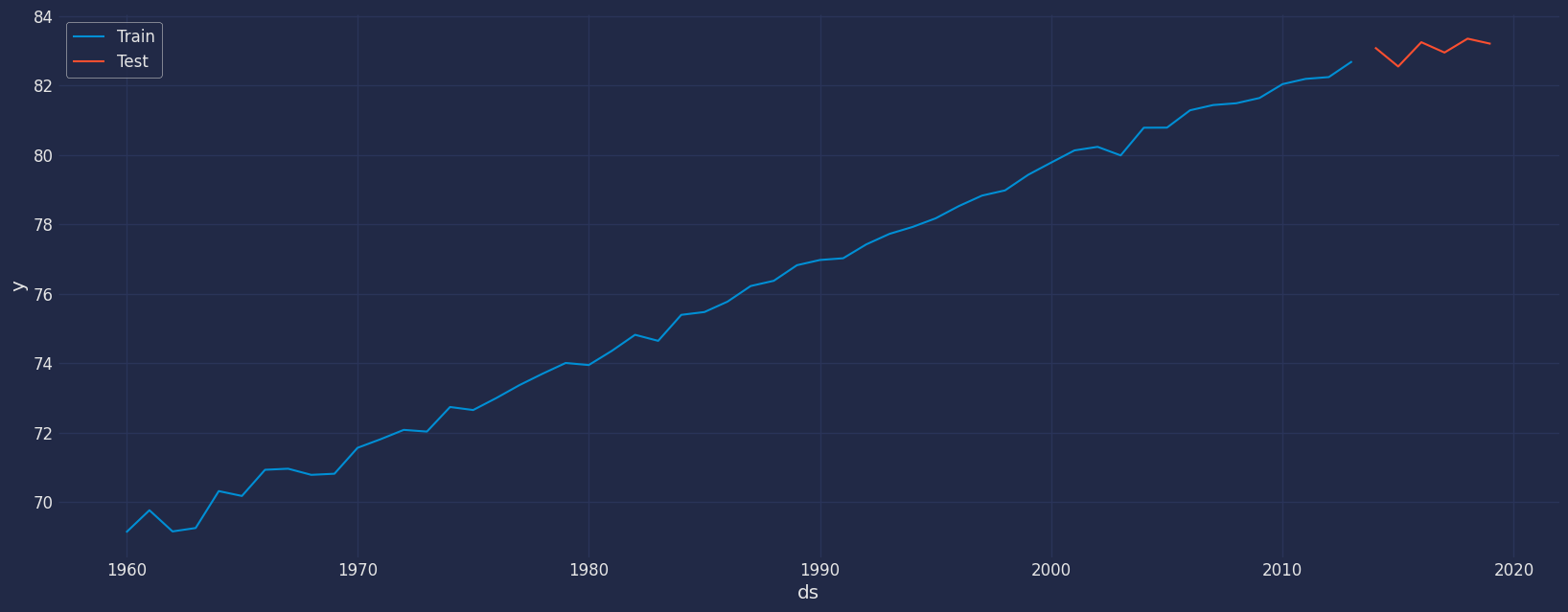

AutoETS的实现

自动选择最佳的ETS (误差、趋势、季节性)模型，使用信息准则。默认使用赤池信息准则（AICc），而特定模型则通过最大似然法估计。状态空间方程的确定可以基于其 $M$ 乘法 $A$ 加法、$Z$ 优化或 $N$ 省略的组成部分。模型字符串参数定义了ETS方程：$E$在$[M,A,Z]$中，$T$在$[N,A,M,Z]$中，$S$在$[N,A,M,Z]$中。

例如，当model='ANN'（加法误差，无趋势，无季节性）时，ETS将只探索简单的指数平滑模型。

如果组件被选择为'Z'，它作为占位符，要求AutoETS模型找出最佳参数。

有关AutoETS模型函数参数的更多信息，列表如下。如需更多信息，请访问文档

model : str
    控制状态空间方程。
season_length : int
    每个时间单位的观察数。例如：24小时数据。
damped : bool
    一个“减弱”趋势的参数。
alias : str
    模型的自定义名称。
prediction_intervals : Optional[ConformalIntervals],
    用于计算符合预测区间的信息。
    默认情况下，模型将计算本地预测区间。

from statsforecast.models import AutoETS

实例化模型

autoets = AutoETS(model=["A","Z","N"],  alias="AutoETS", season_length=1)

拟合模型

autoets = autoets.fit(df["y"].values)
autoets

AutoETS

模型预测

y_hat_dict = autoets.predict(h=6)
y_hat_dict

{'mean': array([83.56937105, 83.65696041, 83.74454977, 83.83213913, 83.91972848,
        84.00731784])}

您可以看到，使用 Arima 模型提取的结果，无论是通过预测还是其他任何方法，都是一个字典。为了提取该结果，我们可以使用 .get() 函数，这将帮助我们提取我们使用的每个方法的字典中每个部分的结果。

forecast=pd.Series(pd.date_range("2014-01-01", freq="ys", periods=6))
forecast=pd.DataFrame(forecast)
forecast.columns=["ds"]
forecast["hat"]=y_hat_dict.get("mean")
forecast["unique_id"]="1"
forecast

	ds	hat	unique_id
0	2014-01-01	83.569371	1
1	2015-01-01	83.656960	1
2	2016-01-01	83.744550	1
3	2017-01-01	83.832139	1
4	2018-01-01	83.919728	1
5	2019-01-01	84.007318	1

sns.lineplot(train,x="ds", y="y", label="Train")
sns.lineplot(test, x="ds", y="y", label="Test")
sns.lineplot(forecast,x="ds", y="hat", label="Forecast",)
plt.show()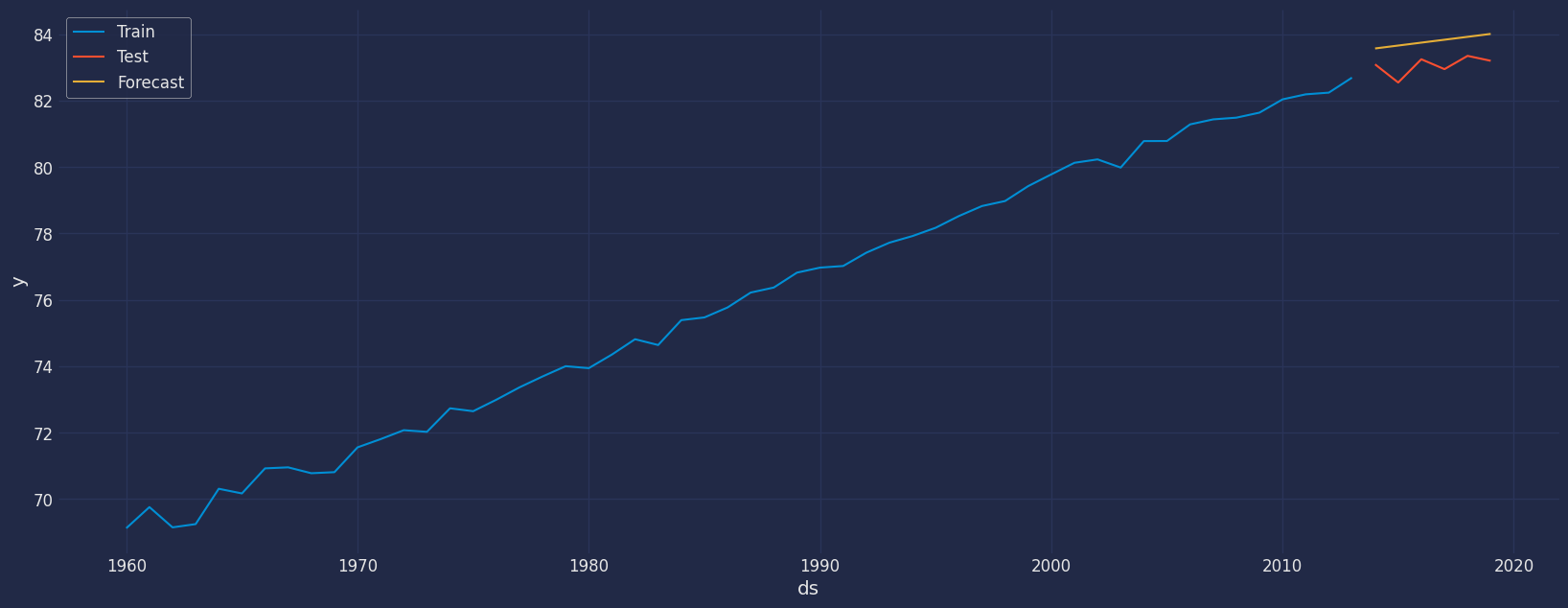

我们来为我们的预测添加置信区间。

y_hat_dict = autoets.predict(h=6, level=[80,90,95])
y_hat_dict

{'mean': array([83.56937105, 83.65696041, 83.74454977, 83.83213913, 83.91972848,
        84.00731784]),
 'lo-95': array([83.09409059, 83.17958519, 83.25889648, 83.32836493, 83.3852606 ,
        83.42814393]),
 'lo-90': array([83.17050311, 83.2563345 , 83.33697668, 83.40935849, 83.4711889 ,
        83.52125977]),
 'lo-80': array([83.25860186, 83.34482153, 83.42699815, 83.50273888, 83.57025872,
        83.62861638]),
 'hi-80': array([83.88014025, 83.96909929, 84.06210139, 84.16153937, 84.26919825,
        84.38601931]),
 'hi-90': array([83.96823899, 84.05758633, 84.15212286, 84.25491976, 84.36826807,
        84.49337591]),
 'hi-95': array([84.04465152, 84.13433563, 84.23020306, 84.33591332, 84.45419637,
        84.58649176])}

forecast["hat"]=y_hat_dict.get("mean")

forecast["lo-80"]=y_hat_dict.get("lo-80")
forecast["hi-80"]=y_hat_dict.get("hi-80")

forecast["lo-90"]=y_hat_dict.get("lo-80")
forecast["hi-90"]=y_hat_dict.get("hi-80")

forecast["lo-95"]=y_hat_dict.get("lo-95")
forecast["hi-95"]=y_hat_dict.get("hi-95")
forecast

	ds	hat	unique_id	lo-80	hi-80	lo-90	hi-90	lo-95	hi-95
0	2014-01-01	83.569371	1	83.258602	83.880140	83.258602	83.880140	83.094091	84.044652
1	2015-01-01	83.656960	1	83.344822	83.969099	83.344822	83.969099	83.179585	84.134336
2	2016-01-01	83.744550	1	83.426998	84.062101	83.426998	84.062101	83.258896	84.230203
3	2017-01-01	83.832139	1	83.502739	84.161539	83.502739	84.161539	83.328365	84.335913
4	2018-01-01	83.919728	1	83.570259	84.269198	83.570259	84.269198	83.385261	84.454196
5	2019-01-01	84.007318	1	83.628616	84.386019	83.628616	84.386019	83.428144	84.586492

df=df.set_index("ds")
forecast=forecast.set_index("ds")

df['unique_id'] = df['unique_id'].astype(object)
df_plot=df.merge(forecast, how='left', on=['unique_id', 'ds'])

fig, ax = plt.subplots()
plt.plot_date(df_plot.index, df_plot["y"],label="Actual", linestyle="-")
plt.plot_date(df_plot.index, df_plot["hat"],label="Forecas", linestyle="-")
ax.fill_between(df_plot.index, 
                df_plot['lo-80'], 
                df_plot['hi-80'],
                alpha=.35,
                color='orange',
                label='AutoETS-level-95')
ax.set_title('', fontsize=22)
ax.set_ylabel('', fontsize=20)
ax.set_xlabel('Timestamp [t]', fontsize=12)
plt.legend(fontsize=12)
ax.grid(True)

plt.show()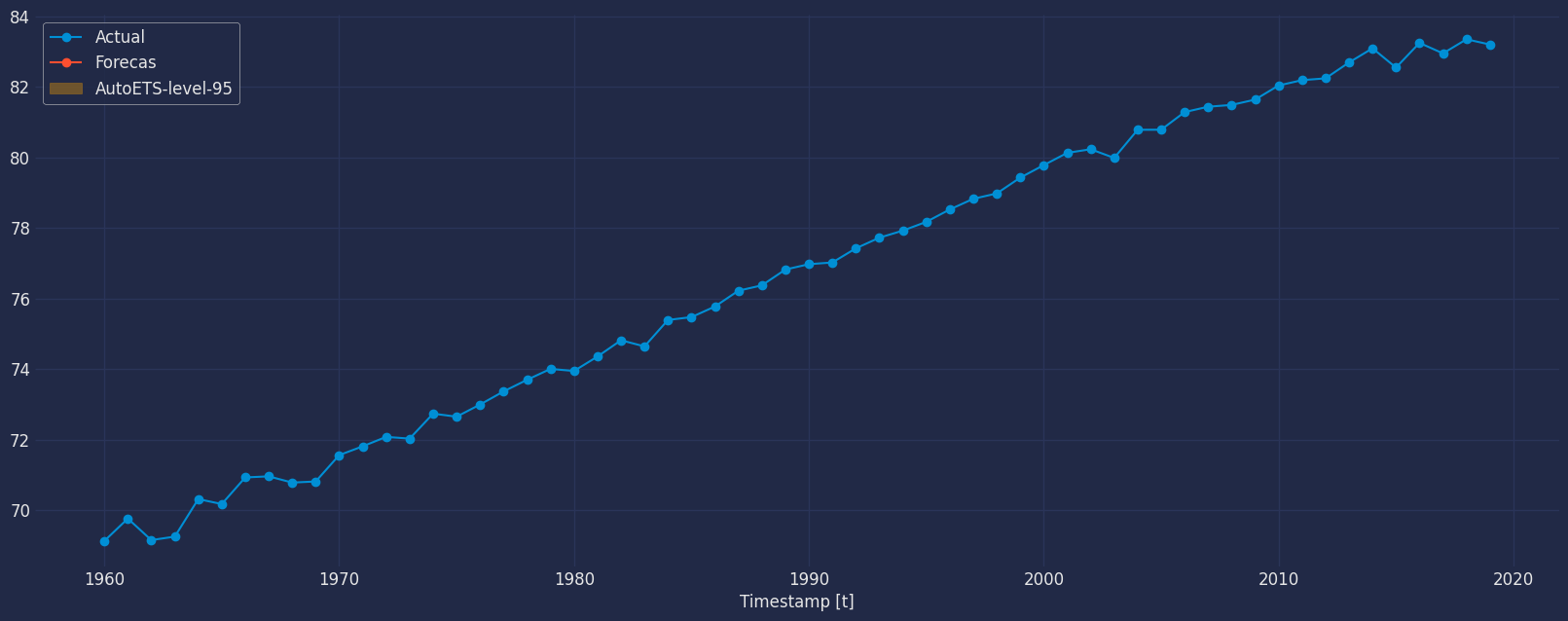

AutoETS.predict_in_sample 方法

访问拟合的指数平滑的样本内预测。

autoets.predict_in_sample()

{'fitted': array([69.11047128, 69.33779313, 69.60481978, 69.82902341, 69.99867608,
        70.19782129, 70.39447403, 70.6410976 , 70.91730954, 71.18057737,
        71.40921444, 71.65195408, 71.90923238, 72.18210689, 72.44032072,
        72.72619326, 73.00461648, 73.28185885, 73.56688287, 73.86376672,
        74.17369207, 74.4619337 , 74.74004938, 75.02518845, 75.27413727,
        75.53397698, 75.78785822, 76.0401374 , 76.30927822, 76.58417332,
        76.88118063, 77.18657633, 77.47625869, 77.76062769, 78.04136835,
        78.31088961, 78.56725183, 78.81937322, 79.07197167, 79.31551239,
        79.56929831, 79.84269161, 80.14276586, 80.45093604, 80.71510722,
        80.98548038, 81.23680745, 81.49249391, 81.74269063, 81.96870832,
        82.16354077, 82.34648092, 82.51452241, 82.65668891, 82.80204272,
        82.97448067, 83.1064133 , 83.2513209 , 83.36754658, 83.4818162 ])}

AutoETS.forecast 方法

内存高效的指数平滑预测。

该方法避免了因对象存储而产生的内存负担。它类似于 fit_predict，但不存储信息。它假设您事先知道预测的时间范围。

autoets.forecast(y=train["y"].values, h=6, fitted=True)

{'mean': array([82.95334067, 83.14710962, 83.34087858, 83.53464753, 83.72841648,
        83.92218543]),
 'fitted': array([69.00631079, 69.23838078, 69.49672275, 69.73753749, 69.95373373,
        70.18800832, 70.42142612, 70.68026343, 70.95296729, 71.21693197,
        71.46051702, 71.70909162, 71.96257898, 72.22173709, 72.47104279,
        72.73363157, 72.99184677, 73.25007587, 73.5140747 , 73.78708229,
        74.07093074, 74.34832297, 74.62600899, 74.91319459, 75.18661412,
        75.47027994, 75.75394823, 76.03846177, 76.33209228, 76.62765077,
        76.93286853, 77.2399741 , 77.53597227, 77.82612695, 78.11104644,
        78.38645253, 78.6510127 , 78.90909424, 79.16292255, 79.40732528,
        79.65260623, 79.90420341, 80.16700064, 80.43291173, 80.67615301,
        80.92469414, 81.16608469, 81.41337419, 81.66169821, 81.90113913,
        82.12727338, 82.34886657, 82.56235691, 82.75957866])}

autoets.forecast(y=train["y"].values, h=6, fitted=True, level=[95])

{'mean': array([82.95334067, 83.14710962, 83.34087858, 83.53464753, 83.72841648,
        83.92218543]),
 'fitted': array([69.00631079, 69.23838078, 69.49672275, 69.73753749, 69.95373373,
        70.18800832, 70.42142612, 70.68026343, 70.95296729, 71.21693197,
        71.46051702, 71.70909162, 71.96257898, 72.22173709, 72.47104279,
        72.73363157, 72.99184677, 73.25007587, 73.5140747 , 73.78708229,
        74.07093074, 74.34832297, 74.62600899, 74.91319459, 75.18661412,
        75.47027994, 75.75394823, 76.03846177, 76.33209228, 76.62765077,
        76.93286853, 77.2399741 , 77.53597227, 77.82612695, 78.11104644,
        78.38645253, 78.6510127 , 78.90909424, 79.16292255, 79.40732528,
        79.65260623, 79.90420341, 80.16700064, 80.43291173, 80.67615301,
        80.92469414, 81.16608469, 81.41337419, 81.66169821, 81.90113913,
        82.12727338, 82.34886657, 82.56235691, 82.75957866]),
 'lo-95': array([82.50120336, 82.69439921, 82.88588753, 83.07456973, 83.2594347 ,
        83.43962264]),
 'hi-95': array([83.40547799, 83.59982004, 83.79586962, 83.99472532, 84.19739825,
        84.40474821]),
 'fitted-lo-95': array([68.5588109 , 68.79088089, 69.04922287, 69.2900376 , 69.50623384,
        69.74050844, 69.97392623, 70.23276354, 70.5054674 , 70.76943209,
        71.01301713, 71.26159173, 71.51507909, 71.7742372 , 72.0235429 ,
        72.28613168, 72.54434688, 72.80257598, 73.06657481, 73.3395824 ,
        73.62343085, 73.90082308, 74.1785091 , 74.4656947 , 74.73911423,
        75.02278005, 75.30644834, 75.59096188, 75.88459239, 76.18015088,
        76.48536864, 76.79247421, 77.08847238, 77.37862706, 77.66354655,
        77.93895264, 78.20351282, 78.46159435, 78.71542266, 78.9598254 ,
        79.20510634, 79.45670352, 79.71950075, 79.98541184, 80.22865312,
        80.47719425, 80.7185848 , 80.96587431, 81.21419832, 81.45363924,
        81.67977349, 81.90136668, 82.11485702, 82.31207877]),
 'fitted-hi-95': array([69.45381068, 69.68588067, 69.94422264, 70.18503738, 70.40123361,
        70.63550821, 70.86892601, 71.12776332, 71.40046717, 71.66443186,
        71.90801691, 72.15659151, 72.41007887, 72.66923698, 72.91854267,
        73.18113146, 73.43934666, 73.69757575, 73.96157459, 74.23458218,
        74.51843063, 74.79582286, 75.07350887, 75.36069448, 75.634114  ,
        75.91777983, 76.20144811, 76.48596166, 76.77959217, 77.07515066,
        77.38036842, 77.68747399, 77.98347215, 78.27362683, 78.55854633,
        78.83395242, 79.09851259, 79.35659413, 79.61042244, 79.85482517,
        80.10010612, 80.35170329, 80.61450053, 80.88041162, 81.1236529 ,
        81.37219402, 81.61358458, 81.86087408, 82.1091981 , 82.34863902,
        82.57477327, 82.79636645, 83.0098568 , 83.20707854])}

AutoETS.forward 方法

autoets.forward(train["y"].values, h=6)

{'mean': array([82.80204272, 82.94739245, 83.09274218, 83.23809191, 83.38344164,
        83.52879137])}

模型评估

判断预测常用的准确性指标有：

平均绝对百分比误差 (MAPE)
平均误差 (ME)
平均绝对误差 (MAE)
平均百分比误差 (MPE)
均方根误差 (RMSE)
实际值与预测值之间的相关性 (corr)

from sklearn import metrics

def model_evaluation(y_true, y_pred, model):
    
    def mean_absolute_percentage_error(y_true, y_pred): 
        y_true, y_pred = np.array(y_true), np.array(y_pred)
        return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
    print (f'Model Evaluation: {model}')
    print(f'MSE is : {metrics.mean_squared_error(y_true, y_pred)}')
    print(f'MAE is : {metrics.mean_absolute_error(y_true, y_pred)}')
    print(f'RMSE is : {np.sqrt(metrics.mean_squared_error(y_true, y_pred))}')
    print(f'MAPE is : {mean_absolute_percentage_error(y_true, y_pred)}')
    print(f'R2 is : {metrics.r2_score(y_true, y_pred)}')
    print(f'corr is : {np.corrcoef(y_true, y_pred)[0,1]}',end='\n\n')

model_evaluation(test["y"], forecast["hat"], "AutoETS")

Model Evaluation: AutoETS
MSE is : 0.5813708312500836
MAE is : 0.7269623343638779
RMSE is : 0.7624767742364902
MAPE is : 0.87594467113361
R2 is : -7.407128931524218
corr is : 0.4910418089228463

致谢

我们要感谢Naren Castellon撰写本教程。

参考文献

Nixtla 自动预测
Rob J. Hyndman 和 George Athanasopoulos (2018). “预测原则与实践，时间序列交叉验证”。

Give us a ⭐ on Github

目录

介绍

指数平滑

所有方法的点预测

创新状态空间模型

ETS(A,N,N)：带有加性误差的简单指数平滑

ETS(M,N,N): 简单指数平滑与乘法误差

ETS(A,A,N): 霍尔特线性方法与加法误差

ETS(M,A,N): 霍尔特线性法与乘法误差

估计ETS模型

模型选择

加载库和数据

读取数据

使用 plot 方法探索数据

自相关图

时间序列的分解

加性时间序列

乘性时间序列

将数据分为训练集和测试集

AutoETS的实现

实例化模型

拟合模型

模型预测

AutoETS.predict_in_sample 方法

AutoETS.forecast 方法

AutoETS.forward 方法

模型评估

致谢

参考文献