保守预测

import warnings
warnings.simplefilter('ignore')

import logging
logging.getLogger('statsforecast').setLevel(logging.ERROR)

在这个例子中，我们将实现保守预测。

前提条件

本教程假设您对StatsForecast有基本的了解。有关最小示例，请访问快速入门

介绍

当我们生成预测时，通常会产生一个被称为点预测的单一值。然而，这个值并不能告诉我们与预测相关的不确定性。要衡量这种不确定性，我们需要预测区间。

预测区间是预测值在特定概率下可能取的一系列值。因此，95%的预测区间应该包含一个值范围，该范围以95%的概率包含实际的未来值。概率预测旨在生成完整的预测分布。另一方面，点预测通常返回该分布的均值或中位数。然而，在现实场景中，最好不仅预测最可能的未来结果，还要预测许多替代结果。

问题在于，有些时间序列模型提供预测分布，而有些模型仅提供点预测。那么我们该如何估计预测的不确定性呢？

预测区间

对于已经提供预测分布的模型，请查看预测区间。

适应性预测

有关视频介绍，请参见 PyData Seattle 讲座。

多分位损失和统计模型可以提供预测区间，但问题在于这些区间是未校准的，这意味着实际观察值落在区间内的频率与其相关的置信水平不一致。例如，一个经过校准的95%预测区间在重复抽样中应包含真实值95%的时间。而一个未校准的95%预测区间则可能仅在80%的时间内包含真实值，或者在99%的时间内包含。在第一种情况下，区间过窄，低估了不确定性，而在第二种情况下，区间过宽，高估了不确定性。

统计方法还假设正态性。在这里，我们讨论另一种称为适应性预测的方法，它不需要任何分布假设。有关该方法的更多信息，请参见 Valery Manokhin 拥有的这个库。

适应性预测区间使用对点预测模型的交叉验证来生成区间。这意味着不需要先验概率，输出也经过良好校准。无需额外训练，模型被视为一个黑箱。该方法与任何模型兼容。

Statsforecast 现在在所有可用模型上支持适应性预测。

安装库

我们假设您已经安装了StatsForecast。如果没有，请查看此指南以获取如何安装StatsForecast的说明。

使用 pip install statsforecast 安装所需的包。

%%capture
pip install statsforecast -U

加载和探索数据

在这个例子中，我们将使用来自M4比赛的每小时数据集。我们首先需要从一个URL下载数据，然后将其加载为pandas数据框。请注意，我们将分别加载训练数据和测试数据。我们还将把测试数据中的y列重命名为y_test。

import pandas as pd 

train = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly.csv')
test = pd.read_csv('https://auto-arima-results.s3.amazonaws.com/M4-Hourly-test.csv').rename(columns={'y': 'y_test'})

train.head()

	unique_id	ds	y
0	H1	1	605.0
1	H1	2	586.0
2	H1	3	586.0
3	H1	4	559.0
4	H1	5	511.0

由于本笔记本的目标是生成预测区间，我们将仅使用数据集中前8个系列，以减少总计算时间。

n_series = 8 
uids = train['unique_id'].unique()[:n_series] # 选择数据集中的前n_series个序列
train = train.query('unique_id in @uids')
test = test.query('unique_id in @uids')

我们可以使用来自 StatsForecast 类的 statsforecast.plot 方法绘制这些系列。这个方法有多个参数，生成本笔记本中图表所需的参数在下面进行了说明。

df：一个包含列 [unique_id, ds, y] 的 pandas 数据框。
forecasts_df：一个包含列 [unique_id, ds] 和模型的 pandas 数据框。
plot_random：bool = True。随机绘制时间序列。
models：List[str]。一个我们想要绘制的模型列表。
level：List[float]。一个我们想要绘制的预测区间列表。
engine：str = matplotlib。它也可以是 matplotlib。 plotly 生成交互式图表，而 matplotlib 生成静态图表。

from statsforecast import StatsForecast

StatsForecast.plot(train, test, plot_random = False, engine = 'plotly')

Unable to display output for mime type(s): application/vnd.plotly.v1+json

训练模型

StatsForecast 可以高效地在不同的时间序列上训练多个模型。这些模型中的大多数可以生成概率预测，这意味着它们可以同时产生点预测和预测区间。

在这个示例中，我们将使用简单指数平滑和 ADIDA，这两者本身不提供预测区间。因此，使用保形预测生成预测区间是合理的。

我们还将展示如何使用 ARIMA 来提供不假设正态性的预测区间。

要使用这些模型，我们首先需要从 statsforecast.models 导入它们，然后我们需要实例化它们。

from statsforecast.models import SeasonalExponentialSmoothing, ADIDA, ARIMA
from statsforecast.utils import ConformalIntervals

# 创建一个模型列表及其实例化参数 
intervals = ConformalIntervals(h=24, n_windows=2)
# 附注：n_windows*h 应小于您的时间序列数据元素总数。
# 另外，n_windows 的值应至少为 2 或更多。

models = [
    SeasonalExponentialSmoothing(season_length=24,alpha=0.1, prediction_intervals=intervals),
    ADIDA(prediction_intervals=intervals),
    ARIMA(order=(24,0,12), season_length=24, prediction_intervals=intervals),
]

要实例化一个新的 StatsForecast 对象，我们需要以下参数：

df：包含训练数据的数据框。
models：在前一步中定义的模型列表。
freq：一个字符串，指示数据的频率。请参见 pandas 可用的频率。
n_jobs：一个整数，指示用于并行处理的作业数量。使用 -1 选择所有核心。

sf = StatsForecast(
    df=train, 
    models=models, 
    freq='H', 
)

现在我们准备生成预测和预测区间。为此，我们将使用 forecast 方法，该方法接受两个参数：

h：一个整数，表示预测的时间范围。在这种情况下，我们将预测接下来的24小时。
level：一个包含置信区间置信水平的浮点数列表。例如，level=[95] 意味着该值范围应以95%的概率包含实际的未来值。

levels = [80, 90] # 预测区间的置信水平 

forecasts = sf.forecast(h=24, level=levels)
forecasts = forecasts.reset_index()
forecasts.head()

	unique_id	ds	SeasonalES	SeasonalES-lo-90	SeasonalES-lo-80	SeasonalES-hi-80	SeasonalES-hi-90	ADIDA	ADIDA-lo-90	ADIDA-lo-80	ADIDA-hi-80	ADIDA-hi-90	ARIMA	ARIMA-lo-90	ARIMA-lo-80	ARIMA-hi-80	ARIMA-hi-90
0	H1	701	624.132690	561.315369	565.365356	682.900024	686.950012	747.292542	668.049988	672.099976	822.485107	826.535095	634.355164	581.760376	585.810364	682.900024	686.950012
1	H1	702	555.698181	501.886902	510.377441	601.018921	609.509460	747.292542	560.200012	570.400024	924.185059	934.385071	578.701355	540.992310	542.581909	614.820801	616.410400
2	H1	703	514.403015	468.656036	471.506042	557.299988	560.150024	747.292542	546.849976	549.700012	944.885071	947.735107	544.308960	528.375244	531.132568	557.485352	560.242676
3	H1	704	482.057892	438.715790	442.315796	521.799988	525.400024	747.292542	508.600006	512.200012	982.385071	985.985107	516.846619	504.739288	504.785309	528.907959	528.953979
4	H1	705	460.222534	419.595062	422.745056	497.700012	500.850006	747.292542	486.149994	489.299988	1005.285095	1008.435059	502.623077	485.736938	488.473846	516.772339	519.509277

绘制预测区间

在这里，我们将使用matplotlib绘制一个时间序列的不同区间。

import matplotlib.pyplot as plt
import numpy as np

def _plot_fcst(fcst, train, model): 
    fig, ax = plt.subplots(1, 1, figsize = (20,7))
    plt.plot(np.arange(0, len(train['y'])), train['y'])
    plt.plot(np.arange(len(train['y']), len(train['y']) + 24), fcst[model], label=model)
    plt.plot(np.arange(len(train['y']), len(train['y']) + 24), fcst[f'{model}-lo-90'], color = 'r', label='lo-90')
    plt.plot(np.arange(len(train['y']), len(train['y']) + 24), fcst[f'{model}-hi-90'], color = 'r', label='hi-90')
    plt.plot(np.arange(len(train['y']), len(train['y']) + 24), fcst[f'{model}-lo-80'], color = 'g', label='lo-80')
    plt.plot(np.arange(len(train['y']), len(train['y']) + 24), fcst[f'{model}-hi-80'], color = 'g', label='hi-80')
    plt.legend()

id = "H105"
temp_train = train.loc[train['unique_id'] == id]
temp_forecast = forecasts.loc[forecasts['unique_id'] == id]

下面所示的季节性指数平滑的预测区间。即使模型生成一个点预测，我们仍然可以得到一个预测区间。80%的预测区间与90%的预测区间没有交叉，这表明这些区间是经过校准的。

_plot_fcst(temp_forecast, temp_train, "SeasonalES")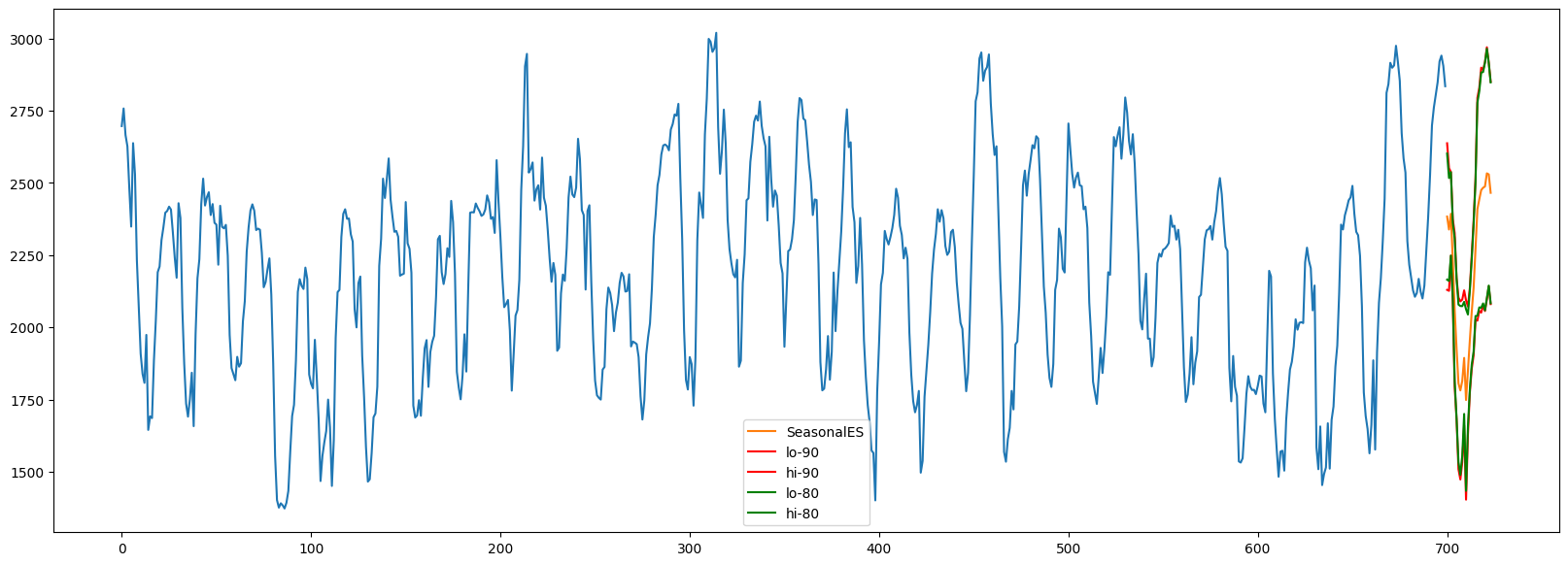

对于拟合较弱的模型，保形预测区间可以更大。较好的模型对应于一个更窄的区间。

_plot_fcst(temp_forecast, temp_train,"ADIDA")

ARIMA是提供预测分布的模型之一，但我们仍然可以使用符合预测来生成预测区间。如前所述，这种方法的一个好处是无需假设正态性。

_plot_fcst(temp_forecast, temp_train,"ARIMA")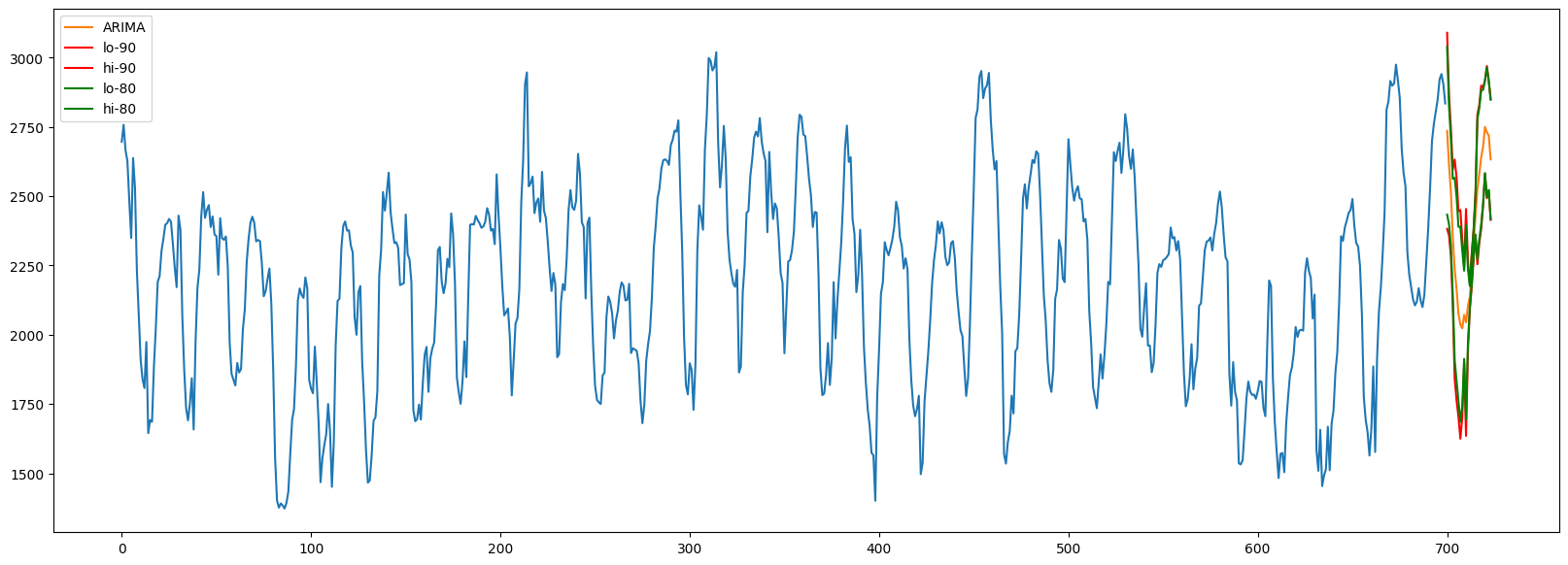

StatsForecast 对象

或者，可以在 StatsForecast 对象上定义预测区间。这将适用于所有没有定义 prediction_intervals 的模型。

from statsforecast.models import SimpleExponentialSmoothing, ADIDA
from statsforecast.utils import ConformalIntervals
from statsforecast import StatsForecast

models = [
    SimpleExponentialSmoothing(alpha=0.1),
    ADIDA()
]

res = StatsForecast(
    df=train, 
    models=models, 
    freq='H').forecast(h=24, prediction_intervals=ConformalIntervals(h=24, n_windows=2), level=[80]) 

res.head().reset_index()

	unique_id	ds	SES	SES-lo-80	SES-hi-80	ADIDA	ADIDA-lo-80	ADIDA-hi-80
0	H1	701	742.669067	672.099976	813.238159	747.292542	672.099976	822.485107
1	H1	702	742.669067	570.400024	914.938110	747.292542	570.400024	924.185059
2	H1	703	742.669067	549.700012	935.638123	747.292542	549.700012	944.885071
3	H1	704	742.669067	512.200012	973.138123	747.292542	512.200012	982.385071
4	H1	705	742.669067	489.299988	996.038147	747.292542	489.299988	1005.285095

未来工作

符合预测已成为一个强大的不确定性量化框架，提供了良好校准的预测区间，而不需要任何分布假设。近年来，它在学术界和工业界的应用迅速增加。我们将继续在这一领域进行研究，未来的教程可能包括：

探索更大的数据集
融入特定行业的示例
调查与符合预测密切相关的专业方法，例如jackknife+（有关jackknife+的详细信息，请参见这里）。

如果您对这些主题或其他相关主题感兴趣，请通过在GitHub上提交问题告知我们。

致谢

我们要感谢Kevin Kho撰写本教程，感谢Valeriy Manokhin在符合预测方面的专业知识，以及对这项工作的推广。

参考文献

Manokhin, Valery. (2022). 机器学习用于概率预测. 10.5281/zenodo.6727505.

Give us a ⭐ on Github