numpy.fft.fftn#
- fft.fftn(a, s=None, axes=None, norm=None, out=None)[源代码]#
计算 N 维离散傅里叶变换.
此函数通过快速傅里叶变换(FFT)计算 M 维数组中任意数量轴上的 N 维离散傅里叶变换.
- 参数:
- aarray_like
输入数组,可以是复杂的.
- s整数序列,可选
输出形状(每个变换轴的长度)(
s[0]指轴 0,``s[1]`` 指轴 1,等等).这对应于fft(x, n)中的n.沿任何轴,如果给定的形状小于输入的形状,则输入被裁剪.如果它更大,则输入用零填充.在 2.0 版本发生变更: 如果它是
-1,则使用整个输入(无填充/修剪).如果 s 未给出,则使用沿由 axes 指定的轴的输入形状.
自 2.0 版本弃用: 如果 s 不是
None,那么 axes 也必须不是None.自 2.0 版本弃用: s 必须只包含
int,不能包含None值.``None`` 值目前意味着在相应的 1-D 变换中使用n的默认值,但这种行为已被弃用.- axes整数序列,可选
要计算FFT的轴.如果没有给出,则使用最后的
len(s)轴,或者如果 s 也没有指定,则使用所有轴.`axes` 中的重复索引意味着在该轴上的变换会执行多次.自 2.0 版本弃用: 如果指定了 s ,则必须显式指定要转换的相应 轴 .
- norm{“backward”, “ortho”, “forward”},可选
在 1.10.0 版本加入.
归一化模式(参见
numpy.fft).默认是”backward”.指示这对前向/后向变换中哪个方向被缩放以及使用什么归一化因子.在 1.20.0 版本加入: 添加了”backward”、”forward”值.
- outcomplex ndarray, 可选
如果提供,结果将被放置在这个数组中.它应该具有适当的形状和 dtype 以适应所有轴(因此与传入除平凡的
s之外的所有内容不兼容).在 2.0.0 版本加入.
- 返回:
- out复杂 ndarray
沿由 axes 指示的轴截断或零填充的输入,或如上述参数部分所述,由 s 和 a 的组合进行变换.
- 引发:
- ValueError
如果 s 和 axes 的长度不同.
- IndexError
如果 axes 的某个元素大于 a 的轴数.
参见
备注
输出与
fft类似,包含所有轴的低阶角中的零频率项,所有轴前半部分的正频率项,所有轴中间的奈奎斯特频率项,以及所有轴后半部分的负频率项,按负频率递减顺序排列.有关详细信息、定义和使用的约定,请参见
numpy.fft.示例
>>> import numpy as np >>> a = np.mgrid[:3, :3, :3][0] >>> np.fft.fftn(a, axes=(1, 2)) array([[[ 0.+0.j, 0.+0.j, 0.+0.j], # may vary [ 0.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]], [[ 9.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]], [[18.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]]]) >>> np.fft.fftn(a, (2, 2), axes=(0, 1)) array([[[ 2.+0.j, 2.+0.j, 2.+0.j], # may vary [ 0.+0.j, 0.+0.j, 0.+0.j]], [[-2.+0.j, -2.+0.j, -2.+0.j], [ 0.+0.j, 0.+0.j, 0.+0.j]]])
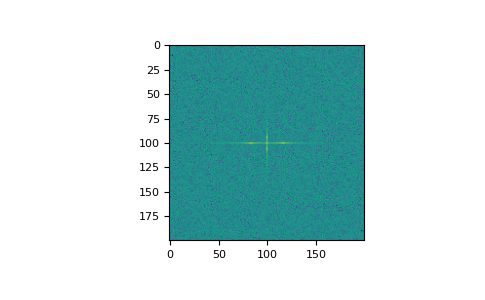
>>> import matplotlib.pyplot as plt >>> [X, Y] = np.meshgrid(2 * np.pi * np.arange(200) / 12, ... 2 * np.pi * np.arange(200) / 34) >>> S = np.sin(X) + np.cos(Y) + np.random.uniform(0, 1, X.shape) >>> FS = np.fft.fftn(S) >>> plt.imshow(np.log(np.abs(np.fft.fftshift(FS))**2)) <matplotlib.image.AxesImage object at 0x...> >>> plt.show()