numpy.random.Generator.normal

方法

random.Generator.normal(loc=0.0, scale=1.0, size=None)

从正态（高斯）分布中随机抽取样本.

正态分布的概率密度函数,由德莫弗首先推导,并在200年后由高斯和拉普拉斯独立推导出来 [2],通常被称为钟形曲线,因为其特征形状（见下面的例子）.

正态分布在自然界中经常出现.例如,它描述了由大量微小的、随机扰动影响的样本的常见分布,每个扰动都有其独特的分布 [2].

参数:

loc浮点数或浮点数的类数组对象

分布的均值（”中心”）.

scale浮点数或浮点数的类数组对象

标准差（分布的扩展或”宽度”）.必须为非负数.

size整数或整数的元组,可选

输出形状.如果给定的形状是,例如,``(m, n, k)``,那么会抽取 m * n * k 个样本.如果大小是 None``（默认）,当 ``loc 和 scale 都是标量时,返回一个单一值.否则,会抽取 np.broadcast(loc, scale).size 个样本.

返回:

outndarray 或标量

从参数化的正态分布中抽取样本.

参见

scipy.stats.norm

概率密度函数、分布或累积密度函数等.

备注

高斯分布的概率密度为

\[p(x) = \frac{1}{\sqrt{ 2 \pi \sigma^2 }} e^{ - \frac{ (x - \mu)^2 } {2 \sigma^2} },\]

其中 \(\mu\) 是均值,:math:sigma 是标准差.标准差的平方,:math:sigma^2,称为方差.

函数在其均值处达到峰值,其”扩散”随标准差增加（函数在 \(x + \sigma\) 和 \(x - \sigma\) 处达到其最大值的 0.607 倍 [2]）.这意味着 normal 更可能返回接近均值的样本,而不是远离均值的样本.

参考文献

[1]

Wikipedia, “正态分布”, https://en.wikipedia.org/wiki/Normal_distribution

[2] (1,2,3)

P. R. Peebles Jr., “Central Limit Theorem” in “Probability, Random Variables and Random Signal Principles”, 4th ed., 2001, pp. 51, 51, 125.

示例

从分布中抽取样本:

>>> mu, sigma = 0, 0.1 # mean and standard deviation
>>> rng = np.random.default_rng()
>>> s = rng.normal(mu, sigma, 1000)

验证均值和方差:

>>> abs(mu - np.mean(s))
0.0  # may vary

>>> abs(sigma - np.std(s, ddof=1))
0.0  # may vary

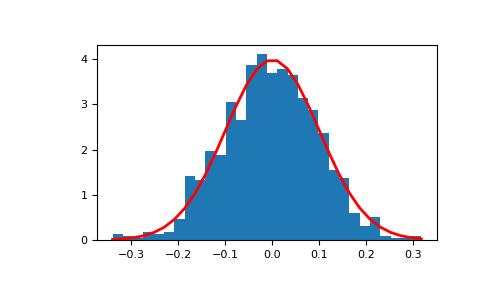
显示样本的直方图,以及概率密度函数:

>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(s, 30, density=True)
>>> plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
...                np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
...          linewidth=2, color='r')
>>> plt.show()

从均值为3、标准差为2.5的正态分布中抽取的2x4样本数组:

>>> rng = np.random.default_rng()
>>> rng.normal(3, 2.5, size=(2, 4))
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],   # random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]])  # random