numpy.random.Generator.pareto

方法

random.Generator.pareto(a, size=None)

从具有指定形状的帕累托 II（又称 Lomax）分布中抽取样本.

参数:

a浮点数或浮点数的类数组对象

分布的形状.必须是正的.

size整数或整数的元组,可选

输出形状.如果给定的形状是,例如,``(m, n, k)``,那么会抽取 m * n * k 个样本.如果大小是 None``（默认）,如果 ``a 是标量,则返回单个值.否则,会抽取 np.array(a).size 个样本.

返回:

outndarray 或标量

从帕累托 II 分布中抽取样本.

参见

scipy.stats.pareto

帕累托I分布

scipy.stats.lomax

Lomax (Pareto II) 分布

scipy.stats.genpareto

广义帕累托分布

备注

帕累托 II 分布的概率密度为

\[p(x) = \frac{a}{{x+1}^{a+1}} , x \ge 0\]

其中 \(a > 0\) 是形状.

帕累托II分布是帕累托I分布的平移和缩放版本,可以在 scipy.stats.pareto 中找到.

参考文献

[1]

Francis Hunt 和 Paul Johnson,关于 Sourceforge 项目的 Pareto 分布.

[2]

帕累托, V. (1896).《政治经济学教程》.洛桑.

[3]

Reiss, R.D., Thomas, M.(2001), 极值的统计分析, Birkhauser Verlag, Basel, pp 23-30.

[4]

Wikipedia, “帕累托分布”, https://en.wikipedia.org/wiki/Pareto_distribution

示例

从分布中抽取样本:

>>> a = 3.
>>> rng = np.random.default_rng()
>>> s = rng.pareto(a, 10000)

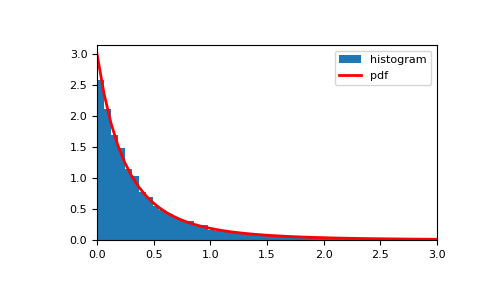
显示样本的直方图,以及概率密度函数:

>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 3, 50)
>>> pdf = a / (x+1)**(a+1)
>>> plt.hist(s, bins=x, density=True, label='histogram')
>>> plt.plot(x, pdf, linewidth=2, color='r', label='pdf')
>>> plt.xlim(x.min(), x.max())
>>> plt.legend()
>>> plt.show()