numpy.random.logistic

random.logistic(loc=0.0, scale=1.0, size=None)

从逻辑分布中抽取样本.

样本是从具有指定参数的对数分布中抽取的,参数包括 loc（位置或均值,也是中位数）和 scale（>0）.

备注

新代码应使用 Generator 实例的 logistic 方法;请参阅 快速开始.

参数:

loc浮点数或浮点数的类数组对象,可选

分布的参数.默认值是0.

scale浮点数或浮点数的类数组对象,可选

分布的参数.必须是非负的.默认值为1.

size整数或整数的元组,可选

输出形状.如果给定的形状是,例如,``(m, n, k)``,那么会抽取 m * n * k 个样本.如果大小是 None``（默认）,当 ``loc 和 scale 都是标量时,返回一个单一值.否则,会抽取 np.broadcast(loc, scale).size 个样本.

返回:

outndarray 或标量

从参数化的逻辑分布中抽取样本.

参见

scipy.stats.logistic

概率密度函数、分布或累积密度函数等.

random.Generator.logistic

应用于新代码.

备注

Logistic 分布的概率密度为

\[P(x) = P(x) = \frac{e^{-(x-\mu)/s}}{s(1+e^{-(x-\mu)/s})^2},\]

其中 \(\mu\) = 位置 和 \(s\) = 尺度.

Logistic 分布在极值问题中使用,它可以作为 Gumbel 分布的混合,在流行病学中,以及由世界国际象棋联合会（FIDE）使用,在 Elo 等级分系统中,假设每个选手的表现是服从 Logistic 分布的随机变量.

参考文献

[1]

Reiss, R.-D. 和 Thomas M. (2001),《极值的统计分析:从保险、金融、水文和其他领域的应用》,Birkhauser Verlag, Basel, 第132-133页.

[2]

Weisstein, Eric W. “Logistic 分布.” 来自 MathWorld–A Wolfram 网络资源. https://mathworld.wolfram.com/LogisticDistribution.html

[3]

Wikipedia, “Logistic-分布”, https://en.wikipedia.org/wiki/Logistic_distribution

示例

从分布中抽取样本:

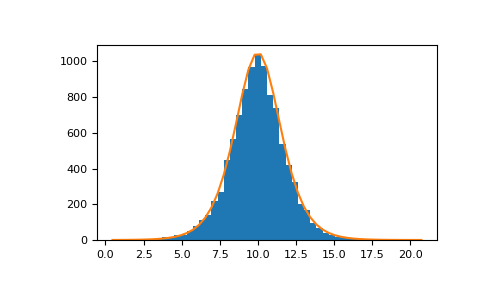
>>> loc, scale = 10, 1
>>> s = np.random.logistic(loc, scale, 10000)
>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, bins=50)

# 绘制分布图

>>> def logist(x, loc, scale):
...     return np.exp((loc-x)/scale)/(scale*(1+np.exp((loc-x)/scale))**2)
>>> lgst_val = logist(bins, loc, scale)
>>> plt.plot(bins, lgst_val * count.max() / lgst_val.max())
>>> plt.show()