numpy.random.power

random.power(a, size=None)

从指数为正的 a - 1 的幂分布中在 [0, 1] 范围内抽取样本.

也称为幂函数分布.

备注

新代码应使用 Generator 实例的 power 方法;请参阅 快速开始.

参数:

a浮点数或浮点数的类数组对象

分布的参数.必须是非负的.

size整数或整数的元组,可选

输出形状.如果给定的形状是,例如,``(m, n, k)``,那么会抽取 m * n * k 个样本.如果大小是 None``（默认）,如果 ``a 是标量,则返回单个值.否则,会抽取 np.array(a).size 个样本.

返回:

outndarray 或标量

从参数化的幂分布中抽取样本.

引发:

ValueError

如果 a <= 0.

参见

random.Generator.power

应用于新代码.

备注

概率密度函数是

\[P(x; a) = ax^{a-1}, 0 \le x \le 1, a>0.\]

幂函数分布只是帕累托分布的逆.它也可以看作是Beta分布的一个特例.

例如,它用于建模保险索赔的夸大报告.

参考文献

[1]

Christian Kleiber, Samuel Kotz, “统计规模分布在经济学和精算科学中”, Wiley, 2003.

[2]

Heckert, N. A. 和 Filliben, James J. “NIST 手册 148: Dataplot 参考手册, 第二卷: Let 子命令和库函数”, 国家标准技术研究所手册系列, 2003年6月. https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/powpdf.pdf

示例

从分布中抽取样本:

>>> a = 5. # shape
>>> samples = 1000
>>> s = np.random.power(a, samples)

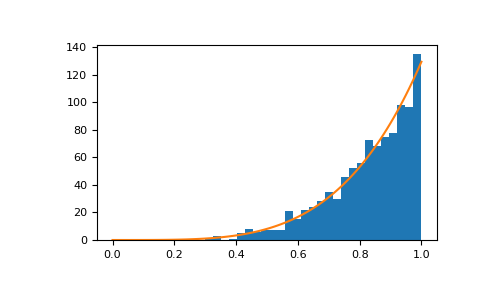
显示样本的直方图,以及概率密度函数:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, bins=30)
>>> x = np.linspace(0, 1, 100)
>>> y = a*x**(a-1.)
>>> normed_y = samples*np.diff(bins)[0]*y
>>> plt.plot(x, normed_y)
>>> plt.show()

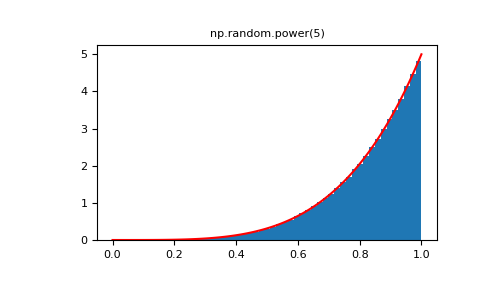
将幂函数分布与帕累托分布的倒数进行比较.

>>> from scipy import stats 
>>> rvs = np.random.power(5, 1000000)
>>> rvsp = np.random.pareto(5, 1000000)
>>> xx = np.linspace(0,1,100)
>>> powpdf = stats.powerlaw.pdf(xx,5)  

>>> plt.figure()
>>> plt.hist(rvs, bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  
>>> plt.title('np.random.power(5)')

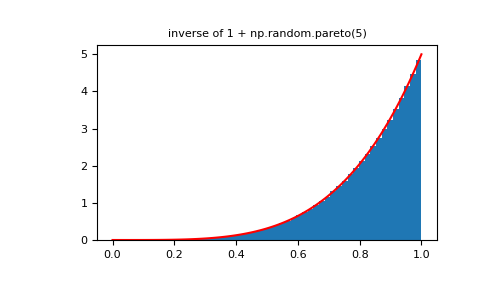
>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  
>>> plt.title('inverse of 1 + np.random.pareto(5)')

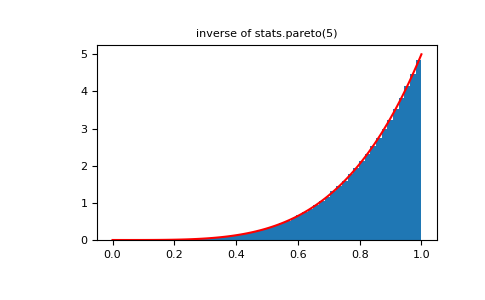
>>> plt.figure()
>>> plt.hist(1./(1.+rvsp), bins=50, density=True)
>>> plt.plot(xx,powpdf,'r-')  
>>> plt.title('inverse of stats.pareto(5)')