numpy.random.standard_cauchy

random.standard_cauchy(size=None)

从模式为0的标准柯西分布中抽取样本.

也称为洛伦兹分布.

备注

新代码应使用 Generator 实例的 standard_cauchy 方法;请参阅 快速开始.

参数:

size整数或整数的元组,可选

输出形状.如果给定的形状是,例如,``(m, n, k)``,那么会抽取 m * n * k 个样本.默认是 None,在这种情况下会返回一个单一值.

返回:

samplesndarray 或标量

抽取的样本.

参见

random.Generator.standard_cauchy

应该用于新代码.

备注

完整柯西分布的概率密度函数是

\[P(x; x_0, \gamma) = \frac{1}{\pi \gamma \bigl[ 1+ (\frac{x-x_0}{\gamma})^2 \bigr] }\]

并且标准柯西分布只需设置 \(x_0=0\) 和 \(\gamma=1\)

柯西分布出现在受迫谐振子问题的解中,也描述了光谱线的展宽.它还描述了在随机角度倾斜的直线在x轴上切割的值的分布.

在研究假设检验时,如果这些检验假设正态性,那么观察这些检验在来自柯西分布的数据上的表现是衡量它们对重尾分布敏感性的一个好指标,因为柯西分布看起来非常像高斯分布,但尾部更重.

参考文献

[1]

NIST/SEMATECH 统计方法电子手册, “柯西分布”, https://www.itl.nist.gov/div898/handbook/eda/section3/eda3663.htm

[2]

Weisstein, Eric W. “柯西分布” 来自 MathWorld–A Wolfram 网络资源. https://mathworld.wolfram.com/CauchyDistribution.html

[3]

Wikipedia, “柯西分布” https://en.wikipedia.org/wiki/Cauchy_distribution

示例

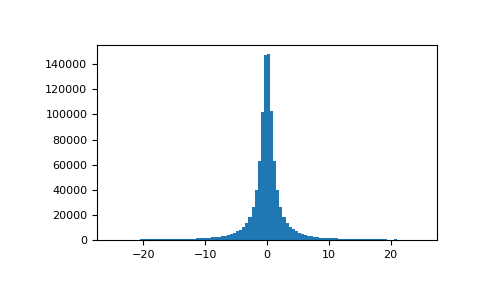
绘制样本并绘制分布图:

>>> import matplotlib.pyplot as plt
>>> s = np.random.standard_cauchy(1000000)
>>> s = s[(s>-25) & (s<25)]  # truncate distribution so it plots well
>>> plt.hist(s, bins=100)
>>> plt.show()