numpy.random.lognormal

random.lognormal(mean=0.0, sigma=1.0, size=None)

从对数正态分布中抽取样本.

从具有指定均值、标准差和数组形状的对数正态分布中抽取样本.请注意,均值和标准差不是分布本身的值,而是其派生的基础正态分布的值.

备注

新代码应使用 Generator 实例的 lognormal 方法;请参阅 快速开始.

参数:

mean浮点数或浮点数的类数组对象,可选

基础正态分布的均值.默认为0.

sigma浮点数或浮点数的类数组对象,可选

基础正态分布的标准差.必须为非负数.默认值为1.

size整数或整数的元组,可选

输出形状.如果给定的形状是,例如,``(m, n, k)``,那么会抽取 m * n * k 个样本.如果大小是 None``（默认）,当 ``mean 和 sigma 都是标量时,返回一个单一值.否则,会抽取 np.broadcast(mean, sigma).size 个样本.

返回:

outndarray 或标量

从参数化的对数正态分布中抽取样本.

参见

scipy.stats.lognorm

概率密度函数, 分布, 累积密度函数, 等等.

random.Generator.lognormal

应该用于新代码.

备注

如果 log(x) 是正态分布的,则变量 x 具有对数正态分布.对数正态分布的概率密度函数为:

\[p(x) = \frac{1}{\sigma x \sqrt{2\pi}} e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}\]

其中 \(\mu\) 是均值,:math:sigma 是变量对数正态分布的标准差.如果随机变量是大量独立同分布变量的*乘积*,则结果是对数正态分布,就像如果变量是大量独立同分布变量的*和*,则结果是正态分布一样.

参考文献

[1]

Limpert, E., Stahel, W. A., 和 Abbt, M., “Log-normal 分布在科学中的应用:关键和线索,” BioScience, 第 51 卷, 第 5 期, 2001 年 5 月. https://stat.ethz.ch/~stahel/lognormal/bioscience.pdf

[2]

Reiss, R.D. 和 Thomas, M., “极值的统计分析,” Basel: Birkhauser Verlag, 2001, pp. 31-32.

示例

从分布中抽取样本:

>>> mu, sigma = 3., 1. # mean and standard deviation
>>> s = np.random.lognormal(mu, sigma, 1000)

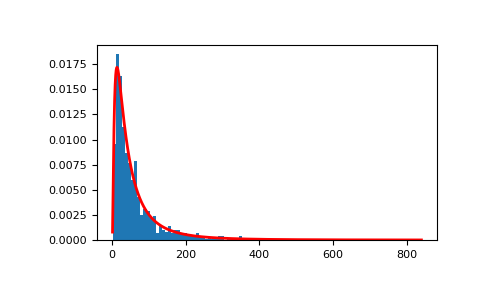
显示样本的直方图,以及概率密度函数:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 100, density=True, align='mid')

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, linewidth=2, color='r')
>>> plt.axis('tight')
>>> plt.show()

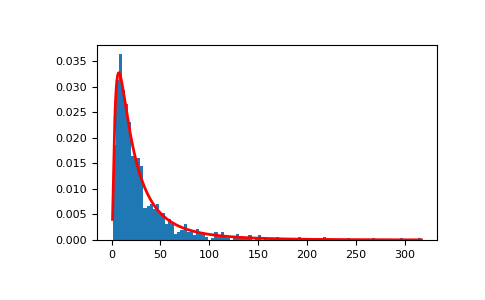
演示从均匀分布中随机抽样的乘积可以很好地由对数正态概率密度函数拟合.

>>> # Generate a thousand samples: each is the product of 100 random
>>> # values, drawn from a normal distribution.
>>> b = []
>>> for i in range(1000):
...    a = 10. + np.random.standard_normal(100)
...    b.append(np.prod(a))

>>> b = np.array(b) / np.min(b) # scale values to be positive
>>> count, bins, ignored = plt.hist(b, 100, density=True, align='mid')
>>> sigma = np.std(np.log(b))
>>> mu = np.mean(np.log(b))

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, color='r', linewidth=2)
>>> plt.show()