1.15. 等渗回归

类 IsotonicRegression 将一个非递减实函数拟合到一维数据。它解决了以下问题：

\[\min \sum_i w_i (y_i - \hat{y}_i)^2\]

受限于 \(\hat{y}_i \le \hat{y}_j\) 当 \(X_i \le X_j\) ，其中权重 \(w_i\) 严格为正，且 X 和 y 均为任意实数。

参数 increasing 将约束改为 \(\hat{y}_i \ge \hat{y}_j\) 当 \(X_i \le X_j\) 。将其设置为 ‘auto’ 将根据 Spearman’s rank correlation coefficient 自动选择约束。

IsotonicRegression 为训练数据生成一系列预测 \(\hat{y}_i\) ，这些预测在均方误差方面最接近目标 \(y\) 。这些预测对未见数据进行插值预测。因此，IsotonicRegression 的预测形成了一个分段线性函数：

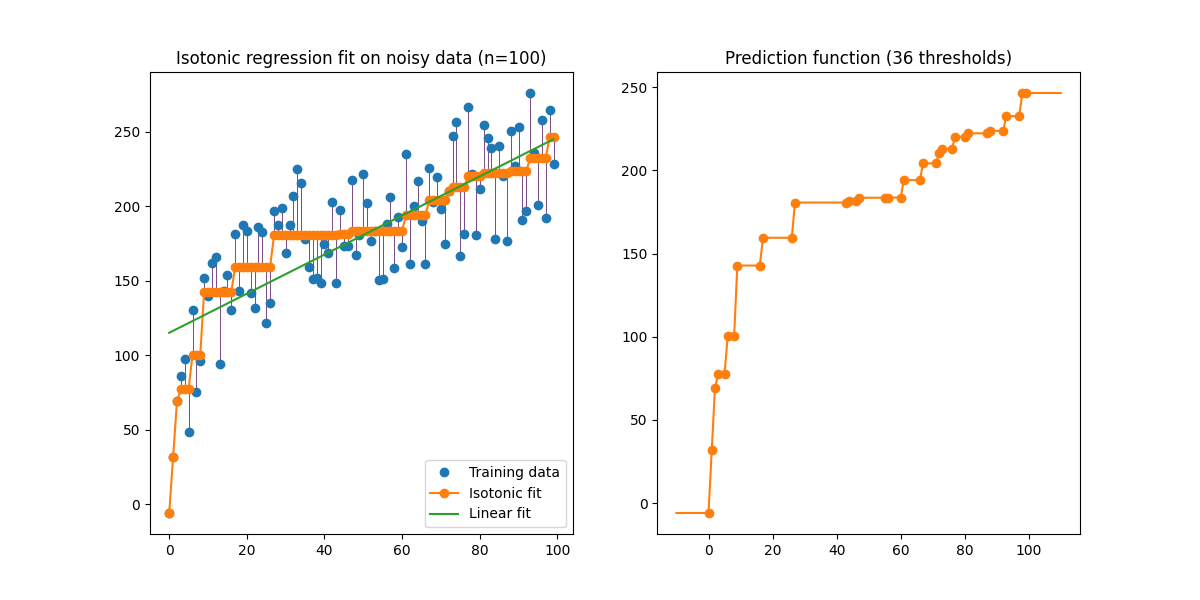
示例

• 保序回归