6.6. 随机投影#

sklearn.random_projection 模块实现了一种简单且计算效率高的方法，通过以可控的精度损失（作为额外的方差）换取更快的处理时间和更小的模型尺寸，来降低数据的维度。该模块实现了两种非结构化的随机矩阵：高斯随机矩阵和稀疏随机矩阵。

随机投影矩阵的维度和分布受到控制，以保持数据集中任意两个样本之间的成对距离。因此，随机投影是一种适用于基于距离方法的近似技术。

参考文献

Sanjoy Dasgupta. 2000. Experiments with random projection. In Proceedings of the Sixteenth conference on Uncertainty in artificial intelligence (UAI’00), Craig Boutilier and Moisés Goldszmidt (Eds.). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 143-151.
Ella Bingham and Heikki Mannila. 2001. Random projection in dimensionality reduction: applications to image and text data. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining (KDD ‘01). ACM, New York, NY, USA, 245-250.

6.6.1. Johnson-Lindenstrauss 引理#

随机投影效率背后的主要理论结果是 Johnson-Lindenstrauss 引理 (引用自 Wikipedia) :

在数学中，Johnson-Lindenstrauss 引理是关于从高维空间到低维空间低失真嵌入点的结果。

转换为低维欧几里得空间。引理表明，高维空间中的一小部分点可以嵌入到一个维度低得多的空间中，使得点之间的距离几乎保持不变。用于嵌入的映射至少是Lipschitz连续的，甚至可以是一个正交投影。

仅知道样本数量， johnson_lindenstrauss_min_dim 保守估计了保证随机投影引入的失真有界的随机子空间的最小尺寸:

>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([    663,   11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894,  9868, 11841])

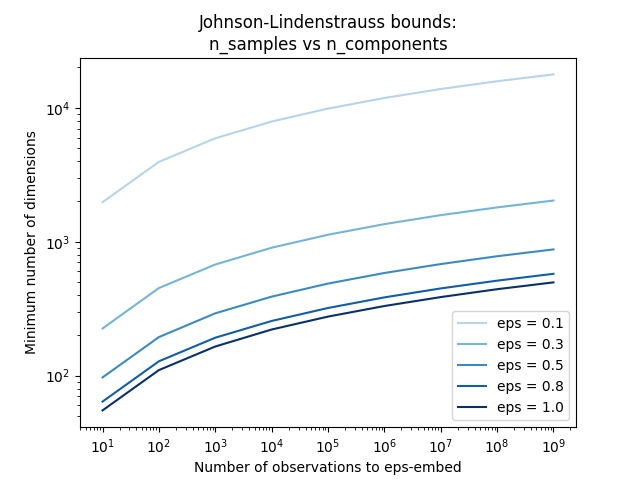
../_images/sphx_glr_plot_johnson_lindenstrauss_bound_001.png

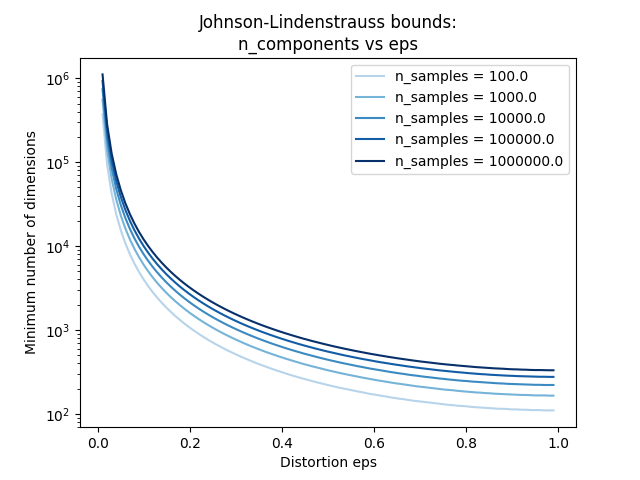
../_images/sphx_glr_plot_johnson_lindenstrauss_bound_002.png

示例

参见使用随机投影进行嵌入的Johnson-Lindenstrauss界限了解关于Johnson-Lindenstrauss引理的理论解释以及使用稀疏随机矩阵的实证验证。

参考文献

Sanjoy Dasgupta 和 Anupam Gupta, 1999. An elementary proof of the Johnson-Lindenstrauss Lemma.

6.6.2. 高斯随机投影#

GaussianRandomProjection 通过将数据投影到随机生成的矩阵上来降低维度。通过将原始输入空间投影到一个随机生成的矩阵上，其中组件是从以下分布中抽取的：\(N(0, \frac{1}{n_{components}})\) ，来实现降维。

以下是一个小片段，展示了如何使用高斯随机投影变换器:

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

6.6.3. 稀疏随机投影#

SparseRandomProjection 通过使用稀疏随机矩阵来降低原始输入空间的维度。

稀疏随机矩阵是密集高斯随机投影矩阵的替代方案，它保证了类似的嵌入质量，同时具有更高的内存效率，并允许更快地计算投影数据。

如果我们定义 s = 1 / density ，随机矩阵的元素是从以下分布中抽取的：

\[\begin{split}\left\{ \begin{array}{c c l} -\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\ 0 &\text{with probability} & 1 - 1 / s \\ +\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\ \end{array} \right.\end{split}\]

其中 \(n_{\text{components}}\) 是投影子空间的大小。默认情况下，非零元素的密度设置为 Ping Li 等人推荐的最低密度：\(1 / \sqrt{n_{\text{features}}}\) 。

以下是一个小片段，展示了如何使用稀疏随机投影变换器:

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

参考文献

D. Achlioptas. 2003. 数据库友好的随机投影：Johnson-Lindenstrauss 与二进制 coins . 计算机与系统科学杂志 66 (2003) 671-687.
Ping Li, Trevor J. Hastie, 和 Kenneth W. Church. 2006. 非常稀疏的随机投影. 在第12届ACM SIGKDD国际知识发现与数据挖掘会议(KDD ‘06)的论文集. ACM, 纽约, NY, USA, 287-296.

6.6.4. 逆变换#

随机投影变换器具有 compute_inverse_components 参数。当设置为 True 时，在拟合过程中创建随机 components_ 矩阵后，变换器计算该矩阵的伪逆并将其存储为

inverse_components_ 。 inverse_components_ 矩阵的形状为

\(n_{features} \times n_{components}\) ，并且它始终是一个密集矩阵，无论组件矩阵是稀疏还是密集。因此，根据特征和组件的数量，它可能会使用大量内存。

当调用 inverse_transform 方法时，它计算输入 X 和逆组件的转置的乘积。如果逆组件在拟合过程中已经计算过，它们会在每次调用 inverse_transform 时被重用。否则它们每次都会重新计算，这可能会很耗时。结果总是密集的，即使 X 是稀疏的。

这里有一个小代码示例，说明如何使用逆变换功能:

>>> import numpy as np
>>> from sklearn.random_projection import SparseRandomProjection
>>> X = np.random.rand(100, 10000)
>>> transformer = SparseRandomProjection(
...   compute_inverse_components=True
... )
...
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
>>> X_new_inversed = transformer.inverse_transform(X_new)
>>> X_new_inversed.shape
(100, 10000)
>>> X_new_again = transformer.transform(X_new_inversed)

>>> np.allclose(X_new, X_new_again)
True