1.7. 高斯过程#

高斯过程 (GP) 是一种非参数的监督学习方法，用于解决 回归 和 概率分类 问题。

高斯过程的优点包括：

  • 预测会插值观测值（至少对于常规核函数）。

  • 预测是概率性的（高斯分布），因此可以计算经验置信区间，并根据这些区间决定是否应在感兴趣的区域重新拟合（在线拟合，自适应拟合）预测。

  • 多才多艺：可以指定不同的 核函数 。提供了常见的核函数，但也可以指定自定义核函数。

高斯过程的缺点包括：

  • 我们的实现不是稀疏的，即它们使用所有样本/特征信息来进行预测。

  • 在高维空间中它们会失去效率——即当特征数量超过几十个时。

1.7.1. 高斯过程回归 (GPR)#

GaussianProcessRegressor 实现了用于回归目的的高斯过程 (GP)。为此，需要指定 GP 的先验。GP 将结合这个先验和基于训练样本的似然函数。它允许通过在预测时给出均值和标准差来给出概率性的预测方法。

../_images/sphx_glr_plot_gpr_noisy_targets_002.png

先验均值假设为常数且为零（对于 normalize_y=False ）或训练数据的均值（对于 normalize_y=True ）。先验的协方差通过传递一个 核函数 对象来指定。超参数 内核的优化在拟合 GaussianProcessRegressor 时通过最大化基于传递的 optimizer 的对数边际似然（LML）来实现。由于 LML 可能具有多个局部最优解，可以通过指定 n_restarts_optimizer 来多次启动优化器。第一次运行总是从内核的初始超参数值开始；后续运行则从允许值范围内随机选择的超参数值开始。如果应保持初始超参数不变，可以将 None 作为优化器传递。

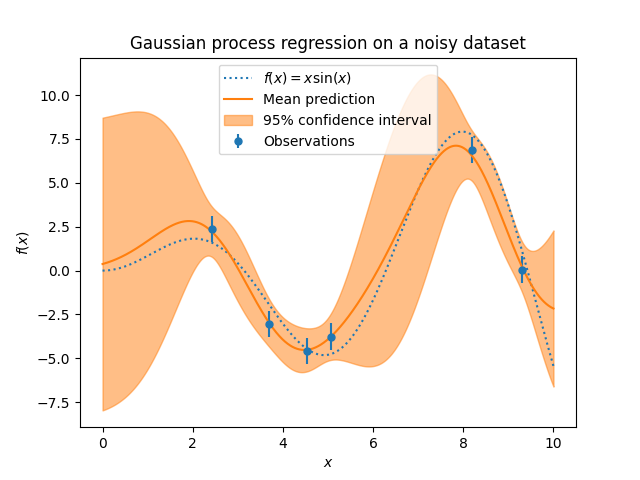
目标中的噪声水平可以通过参数 alpha 传递来指定，全局作为一个标量或每个数据点分别指定。请注意，适度的噪声水平也有助于处理拟合过程中的数值不稳定问题，因为它实际上是通过向内核矩阵的对角线添加噪声来实现的，即作为 Tikhonov 正则化。指定噪声水平的另一种方法是在内核中包含一个 WhiteKernel 组件，它可以估计数据中的全局噪声水平（见下面的示例）。下图显示了通过设置参数 alpha 处理噪声目标的效果。

../_images/sphx_glr_plot_gpr_noisy_targets_003.png

该实现基于 [RW2006] 的算法 2.1。除了标准 scikit-learn 估计器的 API 之外，GaussianProcessRegressor ：

  • 允许在未先进行拟合的情况下进行预测（基于 GP 先验）

  • 提供了一个额外的 sample_y(X) 方法，该方法在给定输入处评估从 GPR（先验或后验）中抽取的样本

  • 公开了一个 log_marginal_likelihood(theta) 方法，该方法可以外部用于其他选择超参数的方式，例如通过马尔可夫链蒙特卡罗方法。

示例

1.7.2. 高斯过程分类 (GPC)#

GaussianProcessClassifier 实现了用于分类目的的高斯过程（GP），更具体地说是用于概率分类，其中测试预测采用类概率的形式。GaussianProcessClassifier 在潜在函数 \(f\) 上放置了一个 GP 先验，然后通过链接函数将其压缩以获得概率分类。潜在函数 \(f\) 是一个所谓的麻烦函数，其值未被观察到且本身并不相关。其目的是允许模型的方便表述，并且在预测过程中 \(f\) 被移除（积分出去）。GaussianProcessClassifier 实现了逻辑链接函数，对于该函数，积分不能以解析形式计算，但在二元情况下很容易近似。

与回归设置相比，潜在函数 \(f\) 的后验即使在 GP 先验下也不是高斯分布，因为高斯似然不适用于离散类别标签。相反，使用了对应于逻辑链接函数（logit）的非高斯似然。GaussianProcessClassifier 基于拉普拉斯近似用高斯近似非高斯后验。更多细节可以在 [RW2006] 的第3章中找到。

GP 先验均值假设为零。先验的协方差通过传递一个 核 对象来指定。核的超参数在 GaussianProcessRegressor 的拟合过程中通过最大化对数边际似然（LML）进行优化。 关于传递的 optimizer 。由于对数边际似然（LML）可能具有多个局部最优解，可以通过指定 n_restarts_optimizer 来重复启动优化器。第一次运行总是从内核的初始超参数值开始；后续运行则从允许值范围内随机选择的超参数值开始。如果应保持初始超参数固定不变，可以将 None 作为优化器传递。

GaussianProcessClassifier 支持多类分类，通过执行基于一对多或一对一的训练和预测。在一对多模式中，每个类别都拟合一个二元高斯过程分类器，该分类器被训练以区分该类别与其他类别。在“一对一”模式中，每对类别都拟合一个二元高斯过程分类器，该分类器被训练以区分这两个类别。这些二元预测器的预测结果被组合成多类预测。有关更多详细信息，请参阅 多类分类 部分。

在高斯过程分类的情况下，“一对一”可能在计算上更便宜，因为它需要解决只涉及整个训练集子集的问题，而不是在整个数据集上解决较少的问题。由于高斯过程分类随数据集大小的立方倍数缩放，这可能会显著加快。然而，请注意，“一对一”不支持预测概率估计，而仅支持普通预测。此外，请注意 GaussianProcessClassifier 尚未实现真正的多类拉普拉斯近似，如上所述，它是基于内部解决多个二元分类任务，并使用一对多或一对一进行组合。

1.7.3. GPC 示例#

1.7.3.1. GPC 的概率预测#

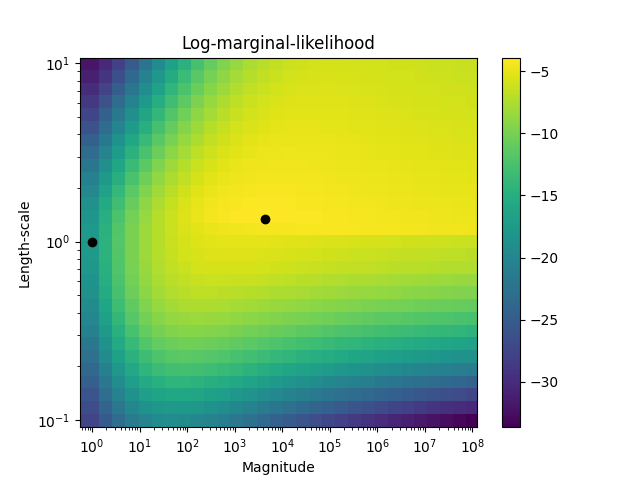
此示例展示了带有 RBF 核的 GPC 的预测概率。 具有不同超参数选择的结果。第一张图显示了使用任意选择的超参数和对应于最大对数边际似然（LML）的超参数的高斯过程分类（GPC）的预测概率。

尽管通过优化LML选择的超参数具有更大的LML，但根据测试数据的对数损失，它们的性能略差。图中显示，这是因为它们在类别边界处表现出急剧的类别概率变化（这是好的），但在远离类别边界的地方预测概率接近0.5（这是不好的）。这种不良效应是由GPC内部使用的拉普拉斯近似引起的。

第二张图显示了不同核函数超参数选择的对数边际似然，用黑色圆点突出显示了第一张图中使用的两种超参数选择。

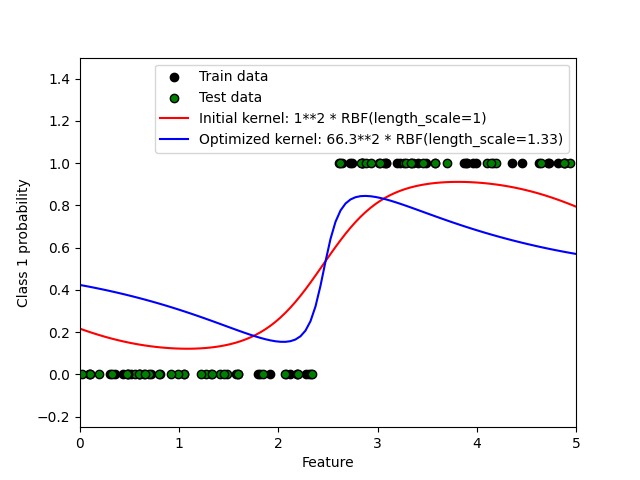
../_images/sphx_glr_plot_gpc_001.png
../_images/sphx_glr_plot_gpc_002.png

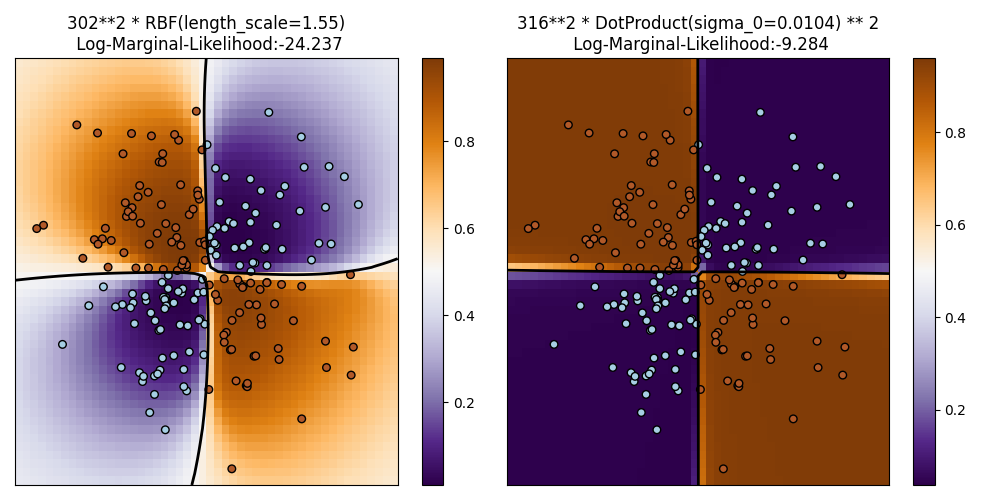
1.7.3.2. 在XOR数据集上的GPC示例#

这个例子展示了在XOR数据上的GPC。比较了静态各向同性核（RBF ）和非静态核（DotProduct ）。在这个特定数据集上，DotProduct 核获得了更好的结果，因为类别边界是线性的并且与坐标轴一致。然而，在实践中，静态核如:class:RBF 通常能获得更好的结果。

../_images/sphx_glr_plot_gpc_xor_001.png

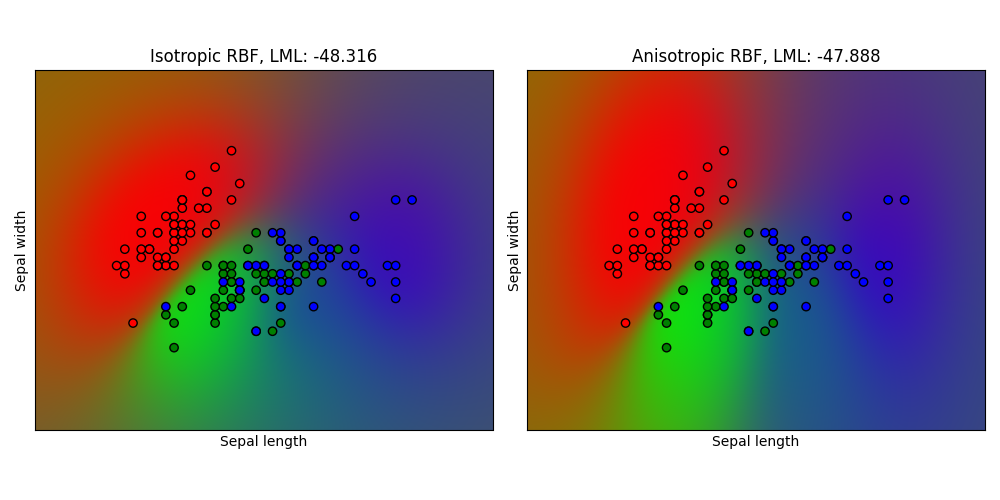
1.7.3.3. 高斯过程分类（GPC）在鸢尾花数据集上的应用#

本示例展示了在鸢尾花数据集的二维版本上，各向同性和各向异性径向基函数（RBF）核的GPC预测概率。这说明了GPC在非二元分类问题上的适用性。各向异性RBF核通过为两个特征维度分配不同的长度尺度，获得了略高的对数边际似然。

../_images/sphx_glr_plot_gpc_iris_001.png

1.7.4. 高斯过程的核函数#

在高斯过程（GP）的背景下，核函数（也称为“协方差函数”）是GP的关键组成部分，它决定了GP的先验和后验的形状。它们通过定义两个数据点的“相似性”并假设相似的数据点应具有相似的目标值，来编码对所学习函数的假设。核函数可以分为两类：平稳核仅依赖于两个数据点之间的距离，而不依赖于它们的绝对值 \(k(x_i, x_j)= k(d(x_i, x_j))\) ，因此在输入空间中的平移变换下是不变的，而非平稳核则还依赖于数据点的具体值。平稳核可以进一步分为各向同性核和各向异性核，其中各向同性核在输入空间中的旋转变换下也是不变的。更多详情，请参阅[RW2006]_的第4章。关于如何最佳组合不同核函数的指导，请参阅[Duv2014]_。

#高斯过程核API

核函数的主要用途是计算数据点之间GP的协方差。为此，可以调用核函数的 __call__ 方法。 该方法可以用于计算二维数组 X 中所有数据点对的“自协方差”，或者二维数组 X 中的数据点与二维数组 Y 中的数据点的所有组合的“交叉协方差”。对于所有核函数 k （除了 WhiteKernel ），以下恒等式成立： k(X) == K(X, Y=X)

如果仅使用自协方差的对角线，可以调用核函数的 diag() 方法，这在计算上比等效的 __call__ 调用更高效： np.diag(k(X, X)) == k.diag(X)

核函数由超参数向量 \(\theta\) 参数化。这些超参数可以控制核函数的长度尺度或周期性等（见下文）。所有核函数都支持通过在 __call__ 方法中设置 eval_gradient=True 来计算核函数自协方差相对于 \(log(\theta)\) 的解析梯度。 也就是说，返回一个 (len(X), len(X), len(theta)) 数组，其中条目 [i, j, l] 包含 \(\frac{\partial k_\theta(x_i, x_j)}{\partial log(\theta_l)}\) 。 这个梯度被高斯过程（回归和分类器）用于计算对数边缘似然函数的梯度，进而用于通过梯度上升确定使对数边缘似然最大化的 \(\theta\) 值。对于每个超参数，在创建核函数实例时需要指定初始值和边界。当前的 \(\theta\) 值可以通过核对象的 theta 属性获取和设置。此外，超参数的边界可以通过核对象的 bounds 属性访问。请注意，这两个属性（theta 和 bounds）返回的是内部使用值的对数变换值，因为这些值通常更适合基于梯度的优化。

每个超参数的规范以一个 Hyperparameter 实例的形式存储在各自的核中。请注意，使用名为 “x” 的超参数的核必须具有属性 self.x 和 self.x_bounds。

所有核的抽象基类是 Kernel 。Kernel 实现了类似于 BaseEstimator 的接口，提供了 get_params() 、 set_params() 和 clone() 方法。这允许通过元估计器（如 Pipeline 或 GridSearchCV ）来设置核值。请注意，由于核的嵌套结构（通过应用核运算符，见下文），核参数的名称可能会变得相对复杂。一般来说，对于二元核运算符，左操作数的参数前缀为 k1__ ，右操作数的参数前缀为 k2__ 。还有一个方便的方法 clone_with_theta(theta) ，它返回一个克隆的核，但将超参数设置为 theta 。一个示例说明：

>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
  k1 : 1**2 * RBF(length_scale=0.5)
  k1__k1 : 1**2
  k1__k1__constant_value : 1.0
  k1__k1__constant_value_bounds : (0.0, 10.0)
  k1__k2 : RBF(length_scale=0.5)
  k1__k2__length_scale : 0.5
  k1__k2__length_scale_bounds : (0.0, 10.0)
  k2 : RBF(length_scale=2)
  k2__length_scale : 2.0
  k2__length_scale_bounds : (0.0, 10.0)
  >>> print(kernel.theta)  # 注意：对数变换
  [ 0.         -0.69314718  0.69314718]
  >>> print(kernel.bounds)  # 注意：对数变换
  [[      -inf 2.30258509]
  [      -inf 2.30258509]
  [      -inf 2.30258509]]

所有高斯过程核函数都与 sklearn.metrics.pairwise 兼容，反之亦然：Kernel 的子类实例可以作为 metric 传递给 sklearn.metrics.pairwise 中的 pairwise_kernels 。此外，通过使用包装类 PairwiseKernel ，来自 pairwise 的核函数可以用作 GP 核。唯一的注意事项是超参数的梯度不是解析的而是数值的，并且所有这些核函数仅支持各向同性距离。参数 gamma 被视为超参数并可能被优化。其他核参数在初始化时直接设置并保持固定。

1.7.4.1. 基本核函数#

ConstantKernel 核函数可以作为 Product 核的一部分，其中它缩放其他因子（核）的幅度，或者作为 Sum 核的一部分，其中它修改高斯过程的均值。它取决于一个参数 \(constant\_value\) 。其定义为：

\[k(x_i, x_j) = constant\_value \;\forall\; x_1, x_2\]

WhiteKernel 核函数的主要用途是作为和核的一部分，其中它解释信号的噪声成分。调整其参数 \(noise\_level\) 对应于估计噪声水平。其定义为：

\[k(x_i, x_j) = noise\_level \text{ 如果 } x_i == x_j \text{ 否则 } 0\]

1.7.4.2. 核函数运算符#

核函数运算符接受一个或两个基本核函数，并将它们组合成一个新的核函数。Sum 核函数接受两个核函数 \(k_1\) 和 \(k_2\) ，并通过 \(k_{sum}(X, Y) = k_1(X, Y) + k_2(X, Y)\) 将它们组合起来。Product 核函数接受两个核函数 \(k_1\) 和 \(k_2\) ，并通过 \(k_{product}(X, Y) = k_1(X, Y) * k_2(X, Y)\) 将它们组合起来。Exponentiation 核函数接受一个基本核函数和一个标量参数 \(p\) ，并通过 \(k_{exp}(X, Y) = k(X, Y)^p\) 将它们组合起来。请注意，核函数对象上的魔法方法 __add__ 、 __mul___ 和 __pow__ 已被重写，因此可以使用例如 RBF() + RBF() 作为 Sum(RBF(), RBF()) 的快捷方式。

1.7.4.3. 径向基函数（RBF）核#

RBF 核是一个平稳核函数。它也被称为“平方指数”核。它由一个长度尺度参数 \(l>0\) 参数化，该参数可以是标量（核函数的各向同性变体）或与输入 \(x\) 具有相同维数的向量（核函数的各向异性变体）。该核函数由以下公式给出：

\[k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)\]

其中 \(d(\cdot, \cdot)\) 是欧几里得距离。这个核函数是无限可微的，这意味着具有此核函数作为协方差函数的GP具有所有阶的均方导数，因此非常平滑。来自RBF核函数的GP的先验和后验如下图所示：

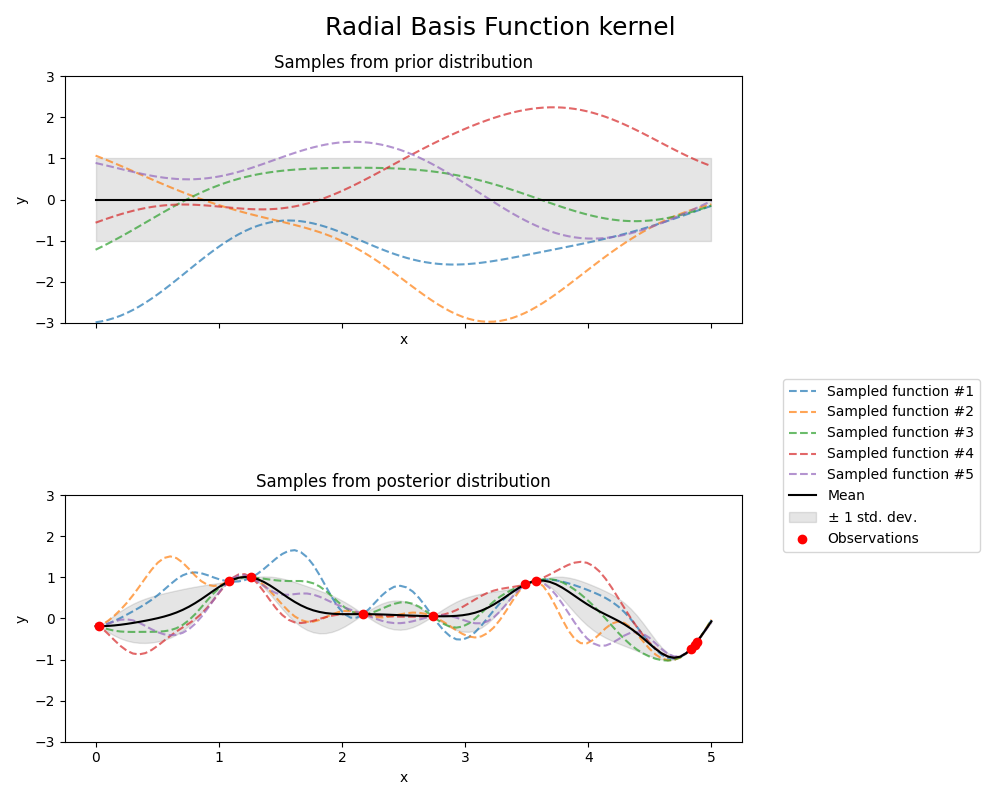
../_images/sphx_glr_plot_gpr_prior_posterior_001.png

1.7.4.4. Matérn 核#

Matern 核是一个平稳核函数，也是径向基函数（RBF）核的泛化。 RBF 核函数。它有一个额外的参数 \(\nu\) ，用于控制结果函数的平滑度。它由一个长度尺度参数 \(l>0\) 参数化，该参数可以是标量（核函数的各向同性变体）或与输入 \(x\) 具有相同维数的向量（核函数的各向异性变体）。

#Matérn 核函数的数学实现

该核函数由以下公式给出：

\[k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),\]

其中 \(d(\cdot,\cdot)\) 是欧几里得距离，\(K_\nu(\cdot)\) 是修正贝塞尔函数，\(\Gamma(\cdot)\) 是伽马函数。 当 \(\nu\rightarrow\infty\) 时，Matérn 核函数收敛到 RBF 核函数。 当 \(\nu = 1/2\) 时，Matérn 核函数变得与绝对指数核函数相同，即

\[k(x_i, x_j) = \exp \Bigg(- \frac{1}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{1}{2}\]

特别是，当 \(\nu = 3/2\) 时：

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{3}}{l} d(x_i , x_j )\Bigg) \exp \Bigg(-\frac{\sqrt{3}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{3}{2}\]

以及当 \(\nu = 5/2\) 时：

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{5}}{l} d(x_i , x_j ) +\frac{5}{3l} d(x_i , x_j )^2 \Bigg) \exp \Bigg(-\frac{\sqrt{5}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{5}{2}\]

这些是学习不是无限可微（如 RBF 核函数所假设的）但至少一次 (\(\nu = 3/2\) ) 或两次可微 (\(\nu = 5/2\) ) 的函数的流行选择。

通过 \(\nu\) 控制学习函数的平滑度的灵活性，可以适应真实底层函数关系的性质。

由 Matérn 核函数产生的 GP 的先验和后验如下图所示： .. figure:: ../auto_examples/gaussian_process/images/sphx_glr_plot_gpr_prior_posterior_005.png

target:

../auto_examples/gaussian_process/plot_gpr_prior_posterior.html

align:

center

关于Matérn核的不同变体的更多细节，请参见[RW2006]_，第84页。

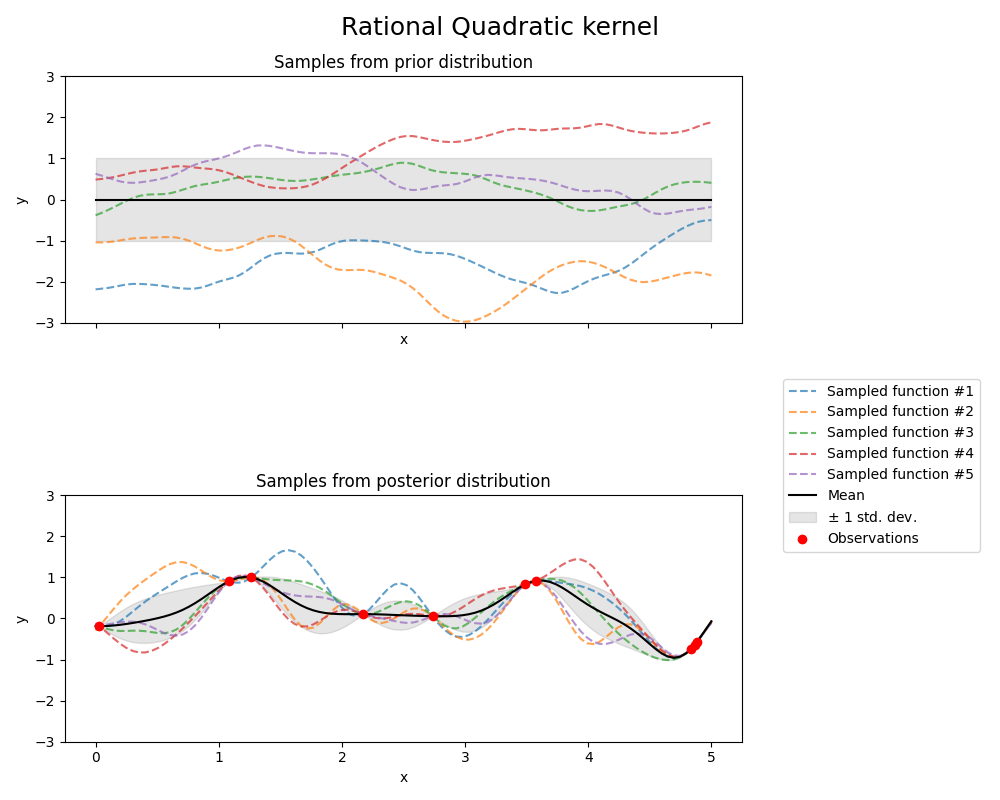
1.7.4.5. 有理二次核#

RationalQuadratic 核可以看作是具有不同特征长度尺度的:class:RBF 核的尺度混合（无限和）。它由长度尺度参数:math:l>0 和尺度混合参数:math:alpha>0 参数化。目前仅支持:math:l 为标量的各向同性变体。该核定义为：

\[k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}\]

由:class:RationalQuadratic 核产生的GP的先验和后验如下图所示：

../_images/sphx_glr_plot_gpr_prior_posterior_002.png

1.7.4.6. Exp-Sine-Squared核#

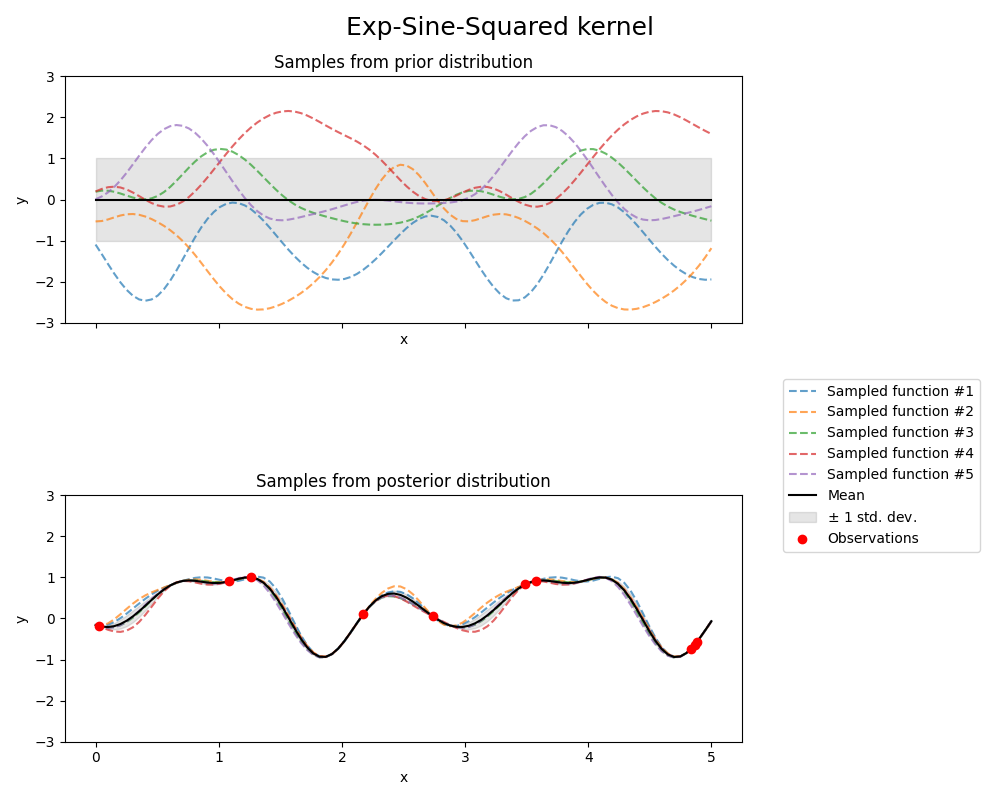
ExpSineSquared 核允许建模周期性函数。它由长度尺度参数:math:l>0 和周期性参数:math:p>0 参数化。目前仅支持:math:l 为标量的各向同性变体。该核定义为：

\[k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)\]

由ExpSineSquared核产生的GP的先验和后验如下图所示：

../_images/sphx_glr_plot_gpr_prior_posterior_003.png

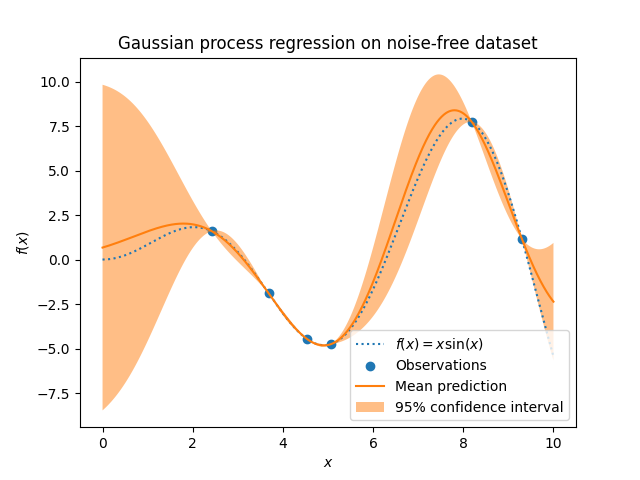
1.7.4.7. 点积核#

DotProduct 核是非平稳的，可以从线性回归中获得。 通过在 \(x_d (d = 1, . . . , D)\) 的系数上放置 \(N(0, 1)\) 先验，并在偏置上放置 \(N(0, \sigma_0^2)\) 先验。DotProduct 核对于原点周围的坐标旋转是不变的，但不具有平移不变性。 它由参数 \(\sigma_0^2\) 参数化。对于 \(\sigma_0^2 = 0\) ，该核称为齐次线性核，否则称为非齐次线性核。该核定义为

\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]

DotProduct 核通常与指数化结合使用。以下图示展示了一个指数为 2 的例子：

../_images/sphx_glr_plot_gpr_prior_posterior_004.png

1.7.4.8. 参考文献#

On this page
Show Source