3.1. 交叉验证：评估估计器性能#

在同一数据上学习预测函数的参数并进行测试是一种方法论上的错误：一个只会重复它刚刚看到的样本标签的模型将获得完美的分数，但在尚未见过的数据上将无法预测任何有用的信息。这种情况称为**过拟合**。为了避免这种情况，在进行（监督）机器学习实验时，通常的做法是将部分可用数据保留为**测试集** X_test, y_test 。请注意，“实验”一词并不只意味着仅用于学术用途，因为在商业环境中，机器学习通常也是从实验开始的。以下是模型训练中典型的交叉验证工作流程流程图。最佳参数可以通过网格搜索技术确定。

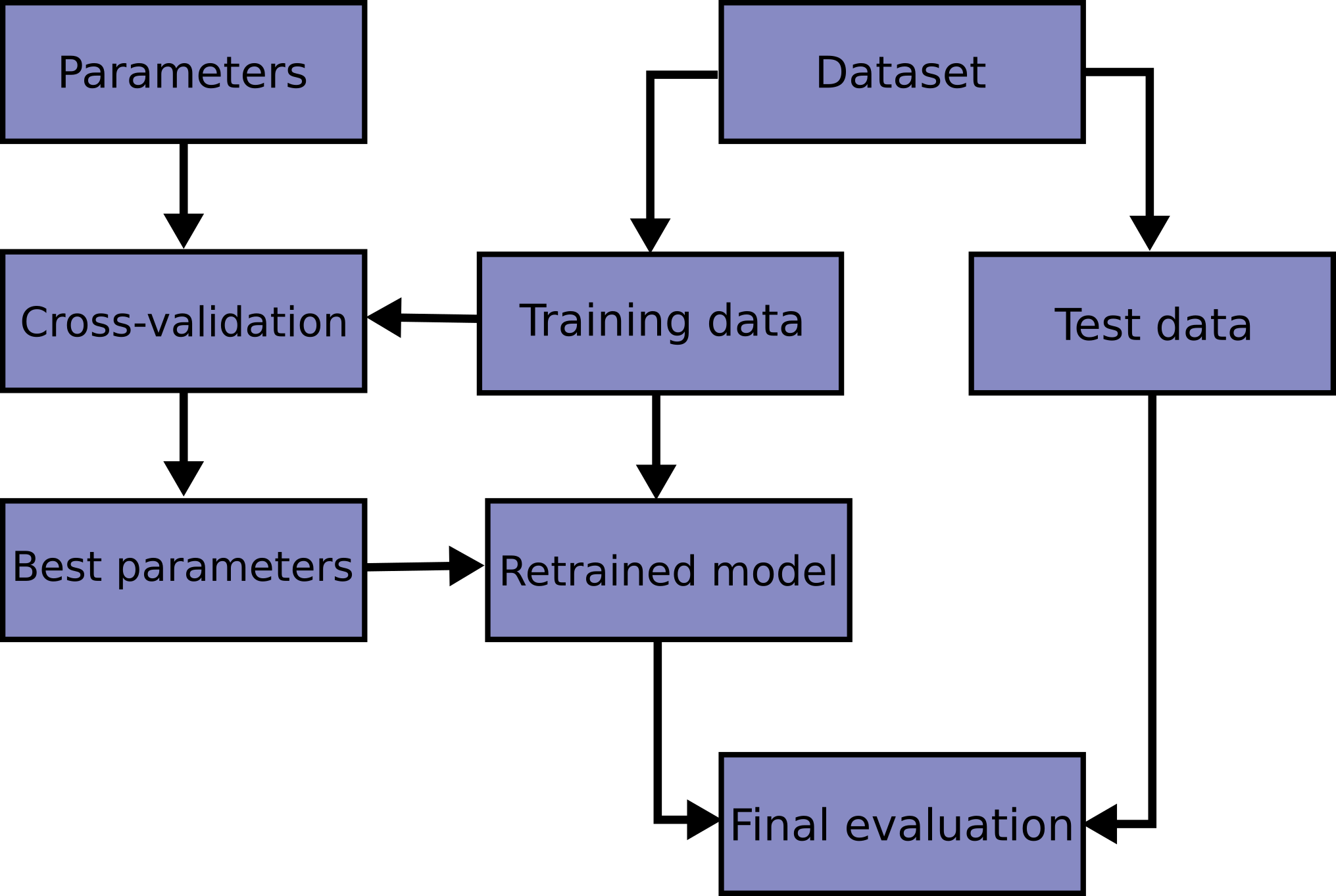
在 scikit-learn 中，可以使用 train_test_split 辅助函数快速计算训练集和测试集的随机分割。让我们加载鸢尾花数据集并对其拟合线性支持向量机:

>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import datasets
>>> from sklearn import svm

>>> X, y = datasets.load_iris(return_X_y=True)
>>> X.shape, y.shape
((150, 4), (150,))

我们现在可以快速采样一个训练集，同时保留40%的数据用于测试（评估）我们的分类器:

>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)

>>> X_train.shape, y_train.shape
((90, 4), (90,))
>>> X_test.shape, y_test.shape
((60, 4), (60,))

>>> clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.96...

在评估估计器的不同设置（“超参数”）时，例如必须为SVM手动设置的 C 设置，仍然存在*在测试集上*过拟合的风险，因为参数可以调整直到估计器表现最优。这样，关于测试集的知识可能会“泄露”到模型中，评估指标不再报告泛化性能。为了解决这个问题，可以将数据集的另一部分保留为所谓的“验证集”：训练在训练集上进行，然后在验证集上进行评估，当实验似乎成功时，最终评估可以在测试集上进行。

然而，通过将可用数据分成三个集合，我们大大减少了可以用于学习模型的样本数量，并且结果可能取决于(训练, 验证)集合对的特定随机选择。

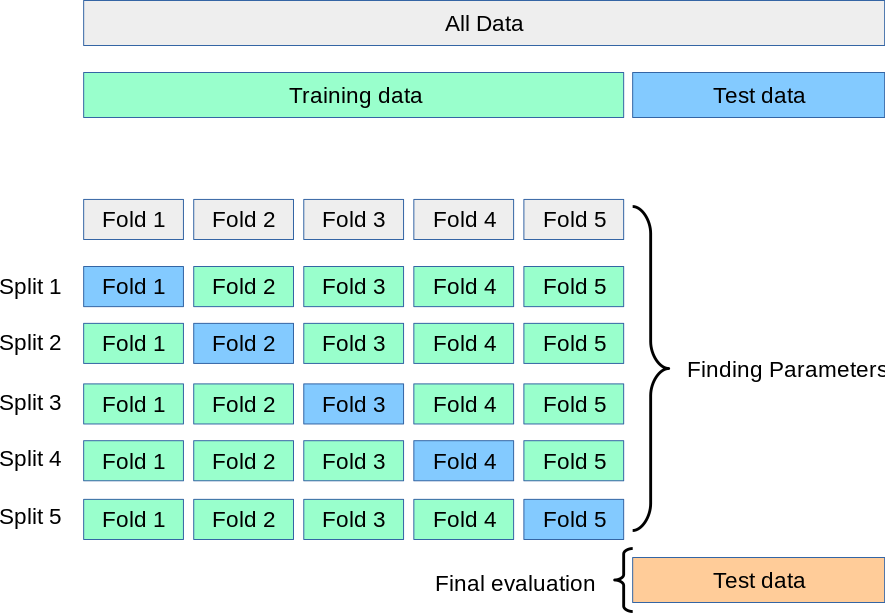
解决这个问题的方法是称为交叉验证（简称CV）的过程。在执行CV时，不再需要验证集，但仍应保留一个测试集用于最终评估。在基本方法中，称为*k*折CV，训练集被分成*k*个较小的集合（下面描述了其他方法，但通常遵循相同的原则）。对于每个*k*“折”，以下过程依次进行：

使用 \(k-1\) 个折作为训练数据训练模型；
在剩余部分数据上验证生成的模型（即，它被用作测试集来计算性能度量，如准确性）。

*k*折交叉验证报告的性能度量是循环中计算的值的平均值。这种方法在计算上可能很昂贵，但没有浪费太多数据。

(正如在固定任意验证集时的情况一样), 这在诸如逆向推理等问题中是一个主要优势，其中样本数量非常小。

3.1.1. 计算交叉验证指标#

使用交叉验证的最简单方法是调用 cross_val_score 辅助函数对估计器和数据集进行操作。

以下示例演示了如何通过分割数据、拟合模型并连续5次计算得分（每次使用不同的分割）来估计线性核支持向量机在鸢尾花数据集上的准确性:

>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1, random_state=42)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores
array([0.96..., 1. , 0.96..., 0.96..., 1. ])

因此，平均得分和标准差给出如下:

>>> print("%0.2f accuracy with a standard deviation of %0.2f" % (scores.mean(), scores.std()))
0.98 accuracy with a standard deviation of 0.02

默认情况下，每次CV迭代计算的得分是估计器的 score 方法。可以通过使用 scoring 参数来改变这一点:

>>> from sklearn import metrics
>>> scores = cross_val_score(
...     clf, X, y, cv=5, scoring='f1_macro')
>>> scores
array([0.96..., 1.  ..., 0.96..., 0.96..., 1.        ])

详情请参见 scoring_parameter 。在鸢尾花数据集中，样本在目标类别之间是平衡的，因此准确性和F1分数几乎相等。

当 cv 参数为整数时，cross_val_score 默认使用 KFold 或 StratifiedKFold 策略，后者在估计器继承自 ClassifierMixin 时使用。 <sklearn.base.ClassifierMixin> `.

也可以通过传递交叉验证迭代器来使用其他交叉验证策略，例如:

>>> from sklearn.model_selection import ShuffleSplit
>>> n_samples = X.shape[0]
>>> cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977..., 0.977..., 1.  ..., 0.955..., 1.        ])

另一个选项是使用一个迭代器，生成 (train, test) 的索引数组，例如:

>>> def custom_cv_2folds(X):
...     n = X.shape[0]
...     i = 1
...     while i <= 2:
...         idx = np.arange(n * (i - 1) / 2, n * i / 2, dtype=int)
...         yield idx, idx
...         i += 1
...
>>> custom_cv = custom_cv_2folds(X)
>>> cross_val_score(clf, X, y, cv=custom_cv)
array([1.        , 0.973...])

3.1.1.1. cross_validate 函数与多指标评估#

:func:` cross_validate 函数与 :func: cross_val_score`在以下两个方面有所不同：

它允许指定多个指标进行评估。
它返回一个包含拟合时间、评分时间（以及可选的训练分数、拟合的估计器、训练测试分割索引）的字典，除了测试分数。

对于单指标评估，其中评分参数是一个字符串、可调用对象或 None，键将是 - ['test_score', 'fit_time', 'score_time']

而对于多指标评估，返回值是一个具有以下键的字典 -

['test_<scorer1_name>', 'test_<scorer2_name>', 'test_<scorer...>', 'fit_time', 'score_time']

return_train_score 默认设置为 False 以节省计算时间。要评估训练集上的分数，您需要将其设置为 True 。您还可以通过设置 return_estimator=True 来保留每个训练集上拟合的估计器。类似地，您可以通过设置 return_indices=True 来保留用于将数据集分割为每个 cv 分割的训练和测试集的训练和测试索引。

多指标可以指定为预定义评分器名称的列表、元组或集合:

>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro', 'recall_macro']
>>> clf = svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores = cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1.  ..., 0.96..., 0.96..., 1.        ])

或者作为一个字典，将评分器名称映射到预定义或自定义评分函数:

>>> from sklearn.metrics import make_scorer
>>> scoring = {'prec_macro': 'precision_macro',
...            'rec_macro': make_scorer(recall_score, average='macro')}
>>> scores = cross_validate(clf, X, y, scoring=scoring,
...                         cv=5, return_train_score=True)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_prec_macro', 'test_rec_macro',
 'train_prec_macro', 'train_rec_macro']
>>> scores['train_rec_macro']
array([0.97..., 0.97..., 0.99..., 0.98..., 0.98...])

以下是使用单个指标的 cross_validate 示例:

>>> scores = cross_validate(clf, X, y,
...                         scoring='precision_macro', cv=5,
...                         return_estimator=True)
>>> sorted(scores.keys())
['estimator', 'fit_time', 'score_time', 'test_score']

3.1.1.2. 通过交叉验证获取预测#

函数 cross_val_predict 与 cross_val_score 具有类似的接口，但返回输入中每个元素在测试集中的预测结果。只有能够将所有元素准确分配到测试集一次的交叉验证策略才能使用（否则会引发异常）。

Warning

关于不恰当使用 cross_val_predict 的注意事项

cross_val_predict 的结果可能与使用 cross_val_score 获得的结果不同，因为元素的分组方式不同。函数 cross_val_score 在交叉验证折叠上取平均值，而 cross_val_predict 仅返回来自多个不同模型的标签（或概率）而不加区分。因此，cross_val_predict 不是衡量泛化误差的适当方法。

函数 cross_val_predict 适用于：

可视化从不同模型获得的预测结果。

模型混合：当集成方法中使用一个监督估计器的预测结果来训练另一个估计器时。

可用的交叉验证迭代器将在以下部分介绍。

示例

3.1.2. 交叉验证迭代器#

以下部分列出了生成索引的实用工具，这些索引可用于根据不同的交叉验证策略生成数据集分割。

3.1.2.1. 独立同分布数据的交叉验证迭代器#

假设某些数据是独立同分布（i.i.d.）的，即所有样本来自同一个生成过程，并且该生成过程对过去生成的样本没有记忆。

以下交叉验证器可以在这种情况下使用。

Note

虽然独立同分布数据是机器学习理论中的常见假设，但在实践中很少成立。如果知道样本是使用时间依赖过程生成的，那么使用时间序列感知的交叉验证方案更为安全。同样，如果知道生成过程具有组结构（从不同主体、实验、测量设备收集的样本），那么使用组间交叉验证更为安全。

3.1.2.1.1. K折#

KFold 将所有样本分成 \(k\) 组样本，称为折叠（如果 \(k = n\) ，这相当于 Leave One Out 策略），大小相等（如果可能）。预测函数使用 \(k - 1\) 个折叠进行学习，剩下的一个折叠用于测试。

在包含 4 个样本的数据集上进行 2 折交叉验证的示例:

>>> import numpy as np
>>> from sklearn.model_selection import KFold

>>> X = ["a", "b", "c", "d"]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]

以下是交叉验证行为的可视化。请注意，KFold 不受类别或组的影响。

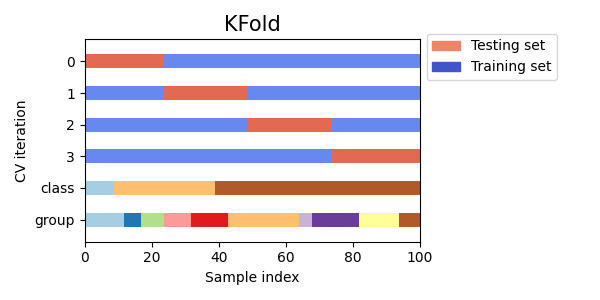
../_images/sphx_glr_plot_cv_indices_006.png

每个折叠由两个数组组成：第一个与 训练集 相关，第二个与 测试集 相关。因此，可以使用 numpy 索引创建训练/测试集:

>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> y = np.array([0, 1, 0, 1])
>>> X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]

3.1.2.1.2. 重复 K 折#

RepeatedKFold 重复 K 折 n 次。当需要运行 KFold n 次，每次产生不同的分割时，可以使用它。

重复 2 次 2 折 K 折的示例:

>>> import numpy as np
>>> from sklearn.model_selection import RepeatedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> random_state = 12883823
>>> rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
>>> for train, test in rkf.split(X):
...     print("%s %s" % (train, test))
...
[2 3] [0 1]
[0 1] [2 3]
[0 2] [1 3]
[1 3] [0 2]

类似地，RepeatedStratifiedKFold 重复分层 K 折 n 次，每次重复中使用不同的随机化。

3.1.2.1.3. 留一法 (LOO)#

LeaveOneOut （或 LOO）是一种简单的交叉验证方法。每个学习集是通过取除一个样本外的所有样本来创建的，测试集是被留下的样本。因此，对于 \(n\) 个样本，我们有 \(n\) 个不同的训练集和 \(n\) 个不同的测试集。这种交叉验证过程不会浪费太多数据，因为只有一个样本从训练集中移除:

>>> from sklearn.model_selection import LeaveOneOut

>>> X = [1, 2, 3, 4]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
...     print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]

使用 LOO 进行模型选择的潜在用户应权衡一些已知的注意事项。与 \(k\) 折交叉验证相比，LOO 从 \(n\) 个样本中构建了 \(n\) 个模型，而不是 \(k\) 个模型，其中 \(n > k\) 。此外，每个模型都是基于 \(n - 1\) 个样本而不是 \((k-1) n / k\) 进行训练的。在这两种方式中，假设 \(k\) 不是太大且 \(k < n\) ，LOO 在计算上比 \(k\) 折交叉验证更昂贵。

在准确性方面，LOO 作为测试误差的估计器通常会导致高方差。直观地说，因为 \(n - 1\) 个 \(n\) 样本被用来构建每个模型，所以从折叠构建的模型几乎彼此相同，并且与从整个训练集构建的模型相同。

然而，如果对于所讨论的训练规模，学习曲线是陡峭的，那么 5 折或 10 折交叉验证可能会高估泛化误差。

作为一般规则，大多数作者和实证证据表明，5 折或 10 折交叉验证应优于 LOO。

3.1.2.1.4. 留P出 (LPO)#

LeavePOut 与 LeaveOneOut 非常相似，因为它通过从完整集合中移除 \(p\) 个样本来创建所有可能的训练/测试集。对于 \(n\) 个样本，这会产生 \({n \choose p}\) 个训练-测试对。与 LeaveOneOut 和 KFold 不同，对于 \(p > 1\) ，测试集将会重叠。

在包含4个样本的数据集上的留2出示例:

>>> from sklearn.model_selection import LeavePOut

>>> X = np.ones(4)
>>> lpo = LeavePOut(p=2)
>>> for train, test in lpo.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]

3.1.2.1.5. 随机排列交叉验证，又称洗牌与分割#

ShuffleSplit 迭代器将生成用户定义数量的独立的训练/测试数据集拆分。样本首先被打乱，然后被分割成一对训练和测试集。

通过显式地为 random_state 伪随机数生成器设定种子，可以控制随机性以重现结果。

以下是使用示例:

>>> from sklearn.model_selection import ShuffleSplit

>>> X = np.arange(10)
>>> ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=0)
>>> for train_index, test_index in ss.split(X):
...     print("%s %s" % (train_index, test_index))
[9 1 6 7 3 0 5] [2 8 4]
[2 9 8 0 6 7 4] [3 5 1]
[4 5 1 0 6 9 7] [2 3 8]
[2 7 5 8 0 3 4] [6 1 9]
[4 1 0 6 8 9 3] [5 2 7]

这里是交叉验证行为的可视化展示。请注意，ShuffleSplit 不受类别或分组的影响。

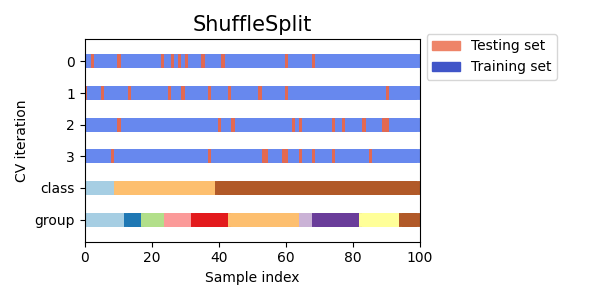
../_images/sphx_glr_plot_cv_indices_008.png

ShuffleSplit 因此是 KFold 交叉验证的一个良好替代方案，它允许对迭代次数和训练/测试拆分中样本的比例进行更精细的控制。

3.1.2.2. 基于类别标签的分层交叉验证迭代器#

一些分类问题可能会在目标类别的分布上表现出很大的不平衡：例如，负样本的数量可能是正样本的几倍。在这种情况下，建议使用分层抽样，如 StratifiedKFold 和 StratifiedShuffleSplit 中实现的那样，以确保每个训练和验证折中的相对类别频率大致保持不变。

3.1.2.2.1. 分层 k-折#

StratifiedKFold 是 k-折 的一种变体，它返回分层折：每个集合包含与完整集合中每个目标类别大致相同的样本百分比。

以下是一个在具有两个不平衡类别的 50 个样本数据集上进行分层 3-折交叉验证的示例。我们展示了每个类别中的样本数量，并与 KFold 进行了比较。

>>> from sklearn.model_selection import StratifiedKFold, KFold
>>> import numpy as np

我们可以看到，StratifiedKFold 在训练集和测试集中都保持了类别比例（大约为 1 / 10）。

以下是交叉验证行为的可视化展示。

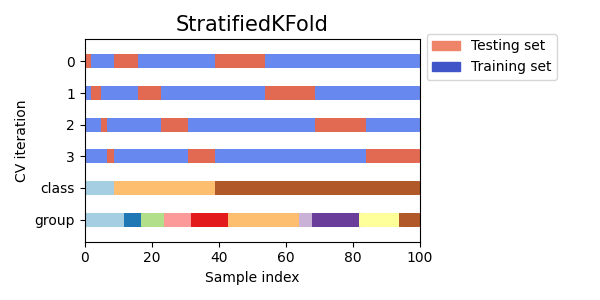
../_images/sphx_glr_plot_cv_indices_009.png

RepeatedStratifiedKFold 可以用于重复 Stratified K-Fold n 次，每次重复中使用不同的随机化。

3.1.2.2.2. 分层随机分割#

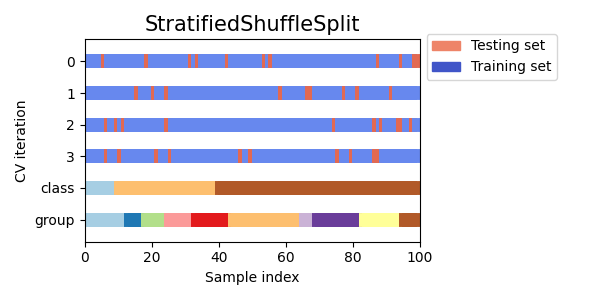
StratifiedShuffleSplit 是 ShuffleSplit 的一种变体，它返回分层分割，即在创建分割时保持与完整数据集中每个目标类别相同的百分比。

以下是交叉验证行为的可视化展示。

../_images/sphx_glr_plot_cv_indices_012.png

3.1.2.3. 预定义的分割/验证集#

对于某些数据集，数据已经预先划分为训练集和验证集，或者已经定义了多个交叉验证集。存在。使用 PredefinedSplit 可以利用这些折叠，例如在搜索超参数时。

例如，当使用验证集时，将 test_fold 设置为 0 表示所有属于验证集的样本，设置为 -1 表示所有其他样本。

3.1.2.4. 分组数据的交叉验证迭代器#

如果基础生成过程产生依赖样本的组，则独立同分布假设被破坏。

这种数据的组是特定于领域的。一个例子是当从多个患者收集的医疗数据，每个患者有多个样本。这样的数据可能依赖于个体组。在我们的例子中，每个样本的患者ID将是其组标识符。

在这种情况下，我们想知道在特定组上训练的模型是否能很好地泛化到未见过的组。为了衡量这一点，我们需要确保验证折叠中的所有样本来自在配对训练折叠中完全没有表示的组。

以下交叉验证分割器可以用于实现这一点。样本的组标识符通过 groups 参数指定。

3.1.2.4.1. 组 k-折#

GroupKFold 是 k-折的一种变体，确保相同的组不会同时出现在测试集和训练集中。例如，如果数据来自不同的受试者，每个受试者有多个样本，如果模型足够灵活，可以从高度个人特定的特征中学习，它可能无法泛化到新的受试者。GroupKFold 可以检测这种过拟合情况。

想象你有三个受试者，每个受试者有一个从 1 到 3 的关联编号:

>>> from sklearn.model_selection import GroupKFold

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]

>>> groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]

>>> gkf = GroupKFold(n_splits=3)
>>> for train, test in gkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[0 1 2 3 4 5] [6 7 8 9]
[0 1 2 6 7 8 9] [3 4 5]
[3 4 5 6 7 8 9] [0 1 2]

每个受试者都在不同的测试折叠中，并且同一个受试者永远不会同时出现在测试和训练中。请注意，由于数据不平衡，折叠的大小并不完全相同。如果类别比例必须在各个折叠中保持平衡，StratifiedGroupKFold 是一个更好的选择。

以下是交叉验证行为的可视化。

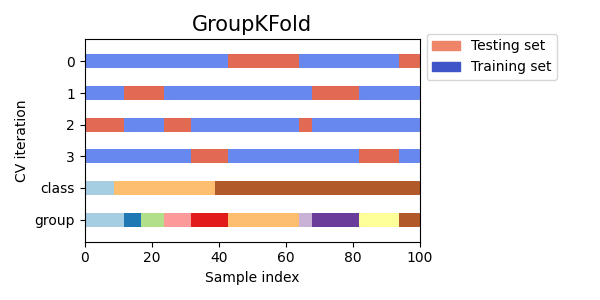
../_images/sphx_glr_plot_cv_indices_007.png

类似于:class:KFold ，GroupKFold 的测试集将形成所有数据的完整分区。与:class:KFold 不同，GroupKFold 完全不进行随机化，而:class:KFold 在 shuffle=True 时进行随机化。

3.1.2.4.2. StratifiedGroupKFold#

StratifiedGroupKFold 是一种结合了:class:StratifiedKFold 和:class:GroupKFold 的交叉验证方案。其思想是尝试在保持每个组在单个分割内的同时，保留每个分割中类别的分布。当你有一个不平衡的数据集时，这可能很有用，因为仅使用:class:GroupKFold 可能会产生偏斜的分割。

示例:

>>> from sklearn.model_selection import StratifiedGroupKFold
>>> X = list(range(18))
>>> y = [1] * 6 + [0] * 12
>>> groups = [1, 2, 3, 3, 4, 4, 1, 1, 2, 2, 3, 4, 5, 5, 5, 6, 6, 6]
>>> sgkf = StratifiedGroupKFold(n_splits=3)
>>> for train, test in sgkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[ 0  2  3  4  5  6  7 10 11 15 16 17] [ 1  8  9 12 13 14]
[ 0  1  4  5  6  7  8  9 11 12 13 14] [ 2  3 10 15 16 17]


[ 1  2  3  8  9 10 12 13 14 15 16 17] [ 0  4  5  6  7 11]

以下是针对不均匀组的交叉验证行为的可视化：

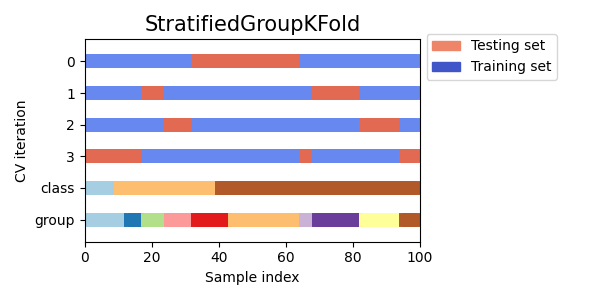
../_images/sphx_glr_plot_cv_indices_005.png

3.1.2.4.3. 留一组法#

LeaveOneGroupOut 是一种交叉验证方案，其中每个分割保留属于一个特定组的样本。组信息通过一个数组提供，该数组编码每个样本所属的组。

因此，每个训练集由除与特定组相关的样本之外的所有样本组成。这与 LeavePGroupsOut 在 n_groups=1 时相同，也与 GroupKFold 在 n_splits 等于传递给 groups 参数的唯一标签数量时相同。

例如，在多个实验的情况下，可以使用 LeaveOneGroupOut 基于不同的实验创建交叉验证：我们使用除一个实验外的所有实验样本创建训练集:

>>> from sklearn.model_selection import LeaveOneGroupOut

>>> X = [1, 5, 10, 50, 60, 70, 80]
>>> y = [0, 1, 1, 2, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3, 3]
>>> logo = LeaveOneGroupOut()
>>> for train, test in logo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[2 3 4 5 6] [0 1]
[0 1 4 5 6] [2 3]
[0 1 2 3] [4 5 6]

另一个常见的应用是使用时间信息：例如，组可以是样本收集的年份，从而允许基于时间分割的交叉验证。

3.1.2.4.4. 留 P 组出#

LeavePGroupsOut 类似于 LeaveOneGroupOut ，但每个训练/测试集移除与 \(P\) 组相关的样本。所有可能的 \(P\) 组组合都被排除，这意味着对于 \(P>1\) ，测试集将重叠。

留 2 组出的示例:

>>> from sklearn.model_selection import LeavePGroupsOut

>>> X = np.arange(6)
>>> y = [1, 1, 1, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3]
>>> lpgo = LeavePGroupsOut(n_groups=2)
>>> for train, test in lpgo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[4 5] [0 1 2 3]
[2 3] [0 1 4 5]
[0 1] [2 3 4 5]

3.1.2.4.5. 组随机分割#

GroupShuffleSplit 迭代器的行为类似于 ShuffleSplit 和 LeavePGroupsOut 的组合，并生成一系列随机分区，其中每个分割保留一组子集。每个训练/测试分割独立执行，这意味着连续的测试集之间没有保证的关系。

以下是使用示例:

>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "a"]
>>> groups = [1, 1, 2, 2, 3, 3, 4, 4]
>>> gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
>>> for train, test in gss.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
...
[0 1 2 3] [4 5 6 7]
[2 3 6 7] [0 1 4 5]
[2 3 4 5] [0 1 6 7]
[4 5 6 7] [0 1 2 3]

以下是交叉验证行为的可视化展示。

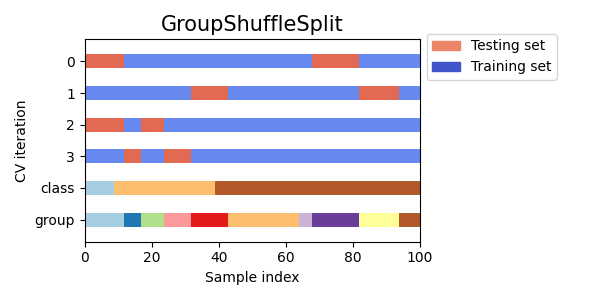
../_images/sphx_glr_plot_cv_indices_011.png

当需要 LeavePGroupsOut 的行为，但组数足够大以至于生成所有可能的分区（其中 \(P\) 组被保留）会非常昂贵时，此类非常有用。在这种情况下，GroupShuffleSplit 提供了由 LeavePGroupsOut 生成的训练/测试分区的随机样本（带替换）。

3.1.2.5. 使用交叉验证迭代器分割训练和测试集#

上述组交叉验证函数也可用于将数据集分割成训练和测试子集。请注意，便捷函数 train_test_split 是 ShuffleSplit 的包装器，因此仅允许使用类别标签进行分层分割，并且无法考虑组。

要执行训练和测试分割，请使用交叉验证分割器的 split() 方法生成的生成器输出的训练和测试子集的索引。例如：

>>> import numpy as np
>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = np.array([0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001])
>>> y = np.array(["a", "b", "b", "b", "c", "c", "c", "a"])
>>> groups = np.array([1, 1, 2, 2, 3, 3, 4, 4])
>>> train_indx, test_indx = next(

… GroupShuffleSplit(random_state=7).split(X, y, groups) … ) >>> X_train, X_test, y_train, y_test = … X[train_indx], X[test_indx], y[train_indx], y[test_indx] >>> X_train.shape, X_test.shape ((6,), (2,)) >>> np.unique(groups[train_indx]), np.unique(groups[test_indx]) (array([1, 2, 4]), array([3]))

3.1.2.6. 时间序列数据的交叉验证#

时间序列数据的特点是观测值之间存在时间上的相关性（自相关）。然而，经典的交叉验证技术如 KFold 和 ShuffleSplit 假设样本是独立且同分布的，这会导致时间序列数据上训练和测试实例之间不合理的相关性（产生泛化误差的糟糕估计）。因此，对于时间序列数据，评估模型时使用那些与训练数据最不相似的“未来”观测值是非常重要的。为了实现这一点，TimeSeriesSplit 提供了一种解决方案。

3.1.2.6.1. 时间序列分割#

TimeSeriesSplit 是 k-折 的一种变体，它将前 \(k\) 折作为训练集，第 \((k+1)\) 折作为测试集。请注意，与标准的交叉验证方法不同，连续的训练集是之前训练集的超集。此外，它将所有多余的数据添加到第一个训练分区，该分区始终用于训练模型。

此类可用于交叉验证在固定时间间隔观测到的时间序列数据样本。

在包含6个样本的数据集上进行3折时间序列交叉验证的示例:

>>> from sklearn.model_selection import TimeSeriesSplit

>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> tscv = TimeSeriesSplit(n_splits=3)
>>> print(tscv)

时间序列分割（TimeSeriesSplit）参数如下：: TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None) >>> for train, test in tscv.split(X): … print(“%s %s” % (train, test)) [0 1 2] [3] [0 1 2 3] [4] [0 1 2 3 4] [5]

以下是交叉验证行为的可视化展示。

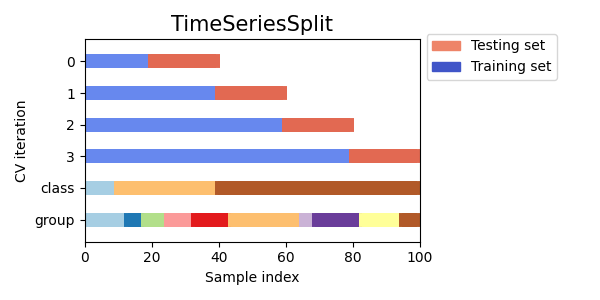
../_images/sphx_glr_plot_cv_indices_013.png

3.1.3. 关于数据洗牌的注意事项#

如果数据排序不是随机的（例如，具有相同类别标签的样本是连续的），首先对其进行洗牌可能是获得有意义的交叉验证结果的关键。然而，如果样本不是独立同分布的，情况可能相反。例如，如果样本对应新闻文章，并且按其发布时间排序，那么对数据进行洗牌可能会导致模型过拟合并夸大验证分数：模型将在与训练样本时间上接近的样本上进行测试，这些样本是人为相似的。

一些交叉验证迭代器，如 KFold ，内置了在分割数据之前洗牌数据索引的选项。请注意：

这比直接洗牌数据消耗更少的内存。
默认情况下不进行洗牌，包括通过指定 cv=some_integer 执行的（分层）K 折交叉验证，如 cross_val_score 、网格搜索等。请记住，train_test_split 仍然返回随机分割。
random_state 参数默认为 None ，这意味着每次迭代 KFold(..., shuffle=True) 时洗牌都会不同。然而， GridSearchCV 将在单次调用其 fit 方法验证的每组参数中使用相同的洗牌。
要使每次分割的结果相同，请将 random_state 设置为整数。

有关如何控制 cv 分割器的随机性以及避免… 常见陷阱，参见控制随机性。

3.1.4. 交叉验证与模型选择#

交叉验证迭代器也可以直接用于使用网格搜索进行模型选择，以找到模型的最优超参数。这是下一节的主题：调整估计器的超参数。

3.1.5. 置换测试分数#

permutation_test_score 提供了另一种评估分类器性能的方法。它提供了一个基于置换的 p 值，表示分类器的观测性能有多大可能是偶然获得的。这个测试中的零假设是分类器未能利用特征和标签之间的任何统计依赖性，在未见数据上做出正确预测。permutation_test_score 通过计算 n_permutations 个不同的数据置换来生成零分布。在每个置换中，标签被随机打乱，从而消除了特征和标签之间的任何依赖性。输出的 p 值是模型在原始数据上获得的交叉验证分数中，模型在置换数据上获得的平均交叉验证分数更好的置换比例。为了获得可靠的结果， n_permutations 通常应大于 100，并且 cv 在 3-10 折之间。

低 p 值提供了证据，表明数据集中存在特征和标签之间的真实依赖关系，并且分类器能够利用这一点获得良好的结果。高 p 值可能是由于特征和标签之间缺乏依赖性（不同类别之间的特征值没有差异），或者是因为分类器未能利用数据中的依赖性。在后一种情况下，使用能够利用数据结构的更合适的分类器，将导致更低的 p 值。

交叉验证提供了关于分类器泛化能力的信息，特别是分类器预期误差的范围。然而，一个在没有结构的高维数据集上训练的分类器，仍然可能在交叉验证中表现比预期更好，仅仅是偶然的。这种情况通常发生在样本数量少于几百的小数据集上。

permutation_test_score 提供了关于分类器是否发现了真实类别结构的信息，并有助于评估分类器的性能。

需要注意的是，即使数据中只有微弱的结构，这个测试也已被证明会产生较低的 p 值，因为在相应的置换数据集中完全没有结构。因此，这个测试只能显示模型何时可靠地优于随机猜测。

最后，permutation_test_score 是通过暴力计算得出的，并在内部拟合了 (n_permutations + 1) * n_cv 个模型。因此，它只适用于拟合单个模型非常快的小数据集。

示例

通过排列检验分类评分的显著性