4.1. 部分依赖图与个体条件期望图#
部分依赖图(PDP)和个体条件期望(ICE)图可以用来可视化和分析目标响应[1]_与一组感兴趣的输入特征之间的交互作用。
PDP[H2009]_和ICE[G2015]_都假设感兴趣的输入特征与补全特征(complement features)是独立的,但这一假设在实践中往往被违反。因此,在存在相关特征的情况下,我们将创建荒谬的数据点来计算PDP/ICE[M2019]_。
4.1.1. 部分依赖图#
部分依赖图(PDP)展示了目标响应与一组感兴趣的输入特征之间的依赖关系,对所有其他输入特征(即“补全”特征)的值进行边缘化处理。直观上,我们可以将部分依赖解释为预期目标响应作为感兴趣输入特征的函数。
由于人类感知的限制,感兴趣的输入特征集的大小必须很小(通常是一个或两个),因此感兴趣的输入特征通常选择在最重要的特征中。
下图展示了自行车共享数据集的两个单向和一个双向部分依赖图,使用的是:class:~sklearn.ensemble.HistGradientBoostingRegressor :
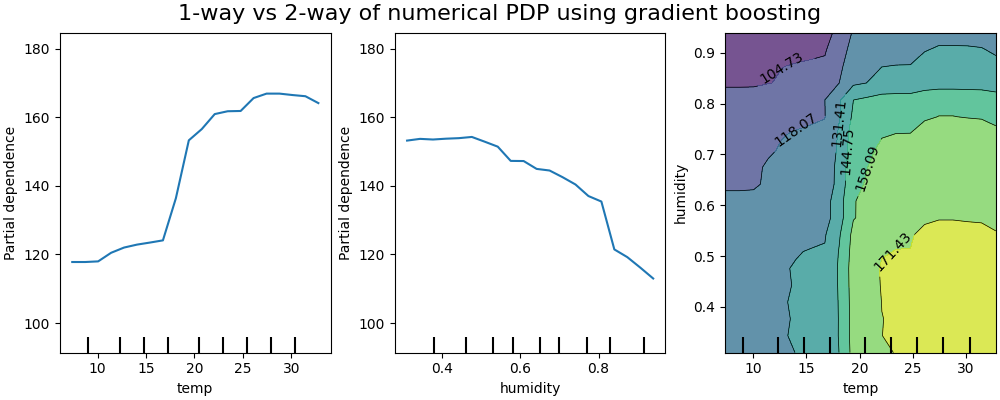
单向PDP告诉我们目标响应与一个感兴趣的输入特征之间的交互作用(例如线性、非线性)。上图中的左图显示了温度对自行车租赁数量的影响;我们可以清楚地看到 较高的温度与较高的自行车租赁数量相关。同样地,我们可以分析湿度对自行车租赁数量的影响(中间图)。因此,这些解释是边际的,一次只考虑一个特征。
具有两个感兴趣输入特征的PDP显示了这两个特征之间的相互作用。例如,上图中的双变量PDP显示了自行车租赁数量对温度和湿度联合值的依赖性。我们可以清楚地看到这两个特征之间的相互作用:在温度高于20摄氏度时,主要是湿度对自行车租赁数量有强烈影响。对于较低的温度,温度和湿度都对自行车租赁数量有影响。
sklearn.inspection 模块提供了一个便利函数 from_estimator 来创建单变量和双变量部分依赖图。在下面的示例中,我们展示了如何创建一个部分依赖图的网格:特征 0 和 1 的单变量PDP以及这两个特征之间的双变量PDP:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import PartialDependenceDisplay
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> PartialDependenceDisplay.from_estimator(clf, X, features)
<...>
你可以使用 plt.gcf() 和 plt.gca() 访问新创建的图形和轴对象。
要创建包含分类特征的部分依赖图,你需要使用参数 categorical_features 指定哪些特征是分类的。该参数接受一个索引列表、分类特征的名称或布尔值。
mask. 分类特征的部分依赖关系的图形表示是条形图或2D热图。
#多类分类的PDP
对于多类分类,您需要通过 target 参数设置要为其创建PDP的类别标签:
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
... max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> PartialDependenceDisplay.from_estimator(mc_clf, X, features, target=0)
<...>
在多输出回归设置中,相同的 target 参数用于指定目标。
如果您需要部分依赖函数的原始值而不是图表,可以使用
sklearn.inspection.partial_dependence 函数:
>>> from sklearn.inspection import partial_dependence
>>> results = partial_dependence(clf, X, [0])
>>> results["average"]
array([[ 2.466..., 2.466..., ...
>>> results["grid_values"]
[array([-1.624..., -1.592..., ...
部分依赖关系应评估的值直接从 X 生成。对于双向部分依赖关系,生成一个2D值网格。
sklearn.inspection.partial_dependence 返回的 values 字段给出了在网格中使用的每个感兴趣输入特征的实际值。它们也对应于图表的轴。
4.1.2. 个体条件期望(ICE)图#
与PDP类似,个体条件期望(ICE)图显示了目标函数与感兴趣的输入特征之间的依赖关系。然而,与显示输入特征平均效应的PDP不同,ICE图单独可视化每个样本的预测与特征的依赖关系,每个样本有一条线。 由于人类感知的局限性,ICE 图仅支持一个感兴趣的输入特征。
下图展示了自行车共享数据集的两个 ICE 图,使用的是 HistGradientBoostingRegressor 。图中绘制了相应的 PD 线叠加在 ICE 线上。
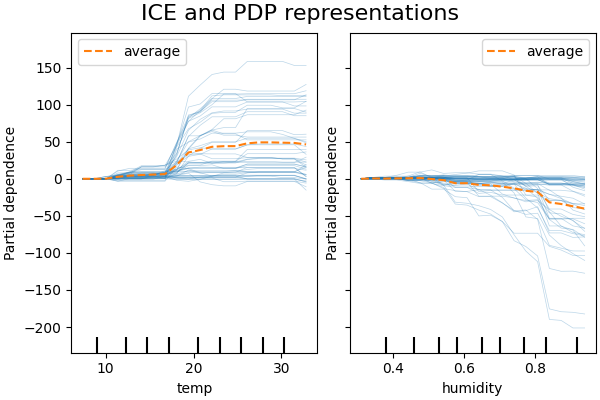
虽然 PDP 擅长显示目标特征的平均效应,但它们可能会掩盖由交互作用产生的异质关系。当存在交互作用时,ICE 图将提供更多的洞察。例如,我们看到温度特征的 ICE 提供了一些额外的信息:一些 ICE 线是平坦的,而其他一些线显示在 35 摄氏度以上温度依赖性下降。我们对湿度特征观察到类似的模式:一些 ICE 线在湿度超过 80% 时显示出急剧下降。
sklearn.inspection 模块的 PartialDependenceDisplay.from_estimator 便捷函数可以通过设置 kind='individual' 来创建 ICE 图。在下面的示例中,我们展示了如何创建一个 ICE 图的网格:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import PartialDependenceDisplay
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1]
>>> PartialDependenceDisplay.from_estimator(clf, X, features,
... kind='individual')
<...>
- 在 ICE 图中,可能不容易看到感兴趣输入特征的平均效应。因此,建议将 ICE 图与 PDP 一起使用。它们可以一起绘制,
kind='both'.>>> PartialDependenceDisplay.from_estimator(clf, X, features, ... kind='both') <...>
如果ICE图中有太多线条,可能会难以看出个体样本之间的差异并解释模型。将ICE图在x轴的第一个值处居中,生成居中的个体条件期望(cICE)图 [G2015]。这强调了个体条件期望与平均线之间的偏离,从而更容易探索异质关系。可以通过设置 centered=True 来绘制cICE图:
>>> PartialDependenceDisplay.from_estimator(clf, X, features,
... kind='both', centered=True)
<...>
4.1.3. 数学定义#
设 \(X_S\) 为感兴趣的输入特征集合(即 features 参数),设 \(X_C\) 为其补集。
响应 \(f\) 在点 \(x_S\) 处的部分依赖定义为:
其中 \(f(x_S, x_C)\) 是给定样本的响应函数(predict 、predict_proba 或 decision_function ),其值由 \(X_S\) 中的特征定义为 \(x_S\) ,由 \(X_C\) 中的特征定义为 \(x_C\) 。注意 \(x_S\) 和 \(x_C\) 可能是元组。
为 \(x_S\) 的不同值计算此积分会产生如上所示的PDP图。ICE线定义为在 \(x_S\) 处评估的单个 \(f(x_{S}, x_{C}^{(i)})\) 。
4.1.4. 计算方法#
有两种主要方法来近似上述积分,即’brute’和’recursion’方法。 method 参数控制使用哪种方法。
‘brute’方法是一种适用于任何估计器的通用方法。请注意,计算ICE图仅支持使用’brute’方法。
通过计算数据 X 上的平均值来近似上述积分:
其中 \(x_C^{(i)}\) 是特征 \(X_C\) 的第 i 个样本值。对于每个 \(x_S\) 的值,此方法需要遍历整个数据集 X ,这在计算上是密集的。
每个 \(f(x_{S}, x_{C}^{(i)})\) 对应于在 \(x_{S}\) 处评估的一条 ICE 线。对多个 \(x_{S}\) 的值进行计算,可以得到完整的 ICE 线。可以看出,ICE 线的平均值对应于部分依赖线。
‘递归’ 方法比 ‘暴力’ 方法更快,但它仅支持某些基于树的估计器的 PDP 图。其计算如下。对于给定点 \(x_S\) ,执行加权树遍历:如果分裂节点涉及感兴趣的输入特征,则跟随相应的左分支或右分支;否则跟随两个分支,每个分支根据进入该分支的训练样本的比例进行加权。最后,部分依赖性由所有访问的叶值的加权平均值给出。
使用 ‘暴力’ 方法时,参数 X 既用于生成 \(x_S\) 的网格值,也用于生成互补特征值 \(x_C\) 。然而,使用 ‘递归’ 方法时, X 仅用于网格值:隐含地,\(x_C\) 的值是训练数据的值。
默认情况下,对于支持它的基于树的估计器,使用 ‘递归’ 方法绘制 PDP,对于其他估计器,使用 ‘暴力’ 方法。
Note
虽然两种方法在一般情况下应该接近,但它们在某些特定设置下可能有所不同。’暴力’ 方法假设存在数据点 \((x_S, x_C^{(i)})\) 。当特征相关时,这种人工样本可能具有非常低的概率质量。’暴力’ 而“递归”方法在部分依赖值的评估上可能会有所不同,因为它们会以不同的方式处理这些不太可能的样本。然而,请记住,解释PDP的主要假设是特征应该是独立的。
示例
脚注
参考文献

