6.3. 数据预处理#

通常，许多学习算法如线性模型受益于数据集的标准化（参见 特征缩放的重要性 ）。如果数据集中存在一些异常值，鲁棒的缩放器或其他转换器可能更为合适。不同缩放器、转换器和规范化器在包含边缘异常值的数据集上的行为在 比较不同缩放器对含有异常值的数据的影响 中有所突出。

6.3.1. 标准化，或均值移除和方差缩放#

数据集的标准化 是 许多在 scikit-learn 中实现的机器学习估计器的常见要求；如果单个特征看起来不像标准正态分布数据（即高斯分布，均值为零，方差为一），它们可能会表现不佳。

在实践中，我们通常忽略分布的形状，只是通过移除每个特征的均值来使数据居中，然后通过将非恒定特征除以其标准差来进行缩放。

例如，在学习算法的优化目标函数中使用的许多元素（如支持向量机的 RBF 核或线性模型的 l1 和 l2 正则化器）可能假设所有特征都以零为中心或在同一数量级上有方差。如果某个特征的方差比其他特征大几个数量级，它可能会主导目标函数，使得估计器无法像预期那样正确地从其他特征中学习。

preprocessing 模块提供了 StandardScaler 工具类，这是一个快速且简便的方法，用于对类似数组的数据集执行以下操作:

>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0., 1., -1.]])
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()

>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])

>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])

>>> X_scaled = scaler.transform(X_train)
>>> X_scaled
array([[ 0.  ..., -1.22...,  1.33...],
       [ 1.22...,  0.  ..., -0.26...],
       [-1.22...,  1.22..., -1.06...]])

缩放后的数据具有零均值和单位方差:

>>> X_scaled.mean(axis=0)
array([0., 0., 0.])

>>> X_scaled.std(axis=0)
array([1., 1., 1.])

此类实现了 Transformer API，以在训练集上计算均值和标准差，以便能够在测试集上重新应用相同的变换。因此，此类适用于 Pipeline 的早期步骤:

>>> from sklearn.datasets import make_classification
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler

>>> X, y = make_classification(random_state=42)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
>>> pipe = make_pipeline(StandardScaler(), LogisticRegression())
>>> pipe.fit(X_train, y_train)  # 对训练数据应用缩放
Pipeline(steps=[('standardscaler', StandardScaler()),

                ('logisticregression', LogisticRegression())])

>>> pipe.score(X_test, y_test)  # 对测试数据应用缩放，不泄露训练数据。
0.96

可以通过传递 with_mean=False 或 with_std=False 到 StandardScaler 的构造函数来禁用中心化或缩放。

6.3.1.1. 将特征缩放到一个范围#

另一种标准化是将特征缩放到给定的最小值和最大值之间，通常是零和一之间， 或者使得每个特征的最大绝对值缩放到单位大小。这可以通过 MinMaxScaler 或 MaxAbsScaler 分别实现。

使用这种缩放的动机包括对特征的标准差非常小的鲁棒性以及在稀疏数据中保留零条目。

以下是一个将玩具数据矩阵缩放到 [0, 1] 范围的示例:

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5       , 0.        , 1.        ],
       [1.        , 0.5       , 0.33333333],
       [0.        , 1.        , 0.        ]])

然后，可以将变换器（transformer）的同一实例应用于在拟合调用期间未见的新测试数据：将应用与训练数据上执行的相同的缩放和平移操作，以保持一致性:

>>> X_test = np.array([[-3., -1.,  4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5       ,  0.        ,  1.66666667]])

可以内省变换器的属性，以了解在训练数据上学到的变换的确切性质:

>>> min_max_scaler.scale_
array([0.5       , 0.5       , 0.33...])

>>> min_max_scaler.min_

array([0. , 0.5 , 0.33…])

如果 MinMaxScaler 被赋予一个显式的 feature_range=(min, max) ，完整的公式是:

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

X_scaled = X_std * (max - min) + min

MaxAbsScaler 的工作方式非常相似，但它以一种使训练数据位于范围 [-1, 1] 内的方式进行缩放，通过除以每个特征中的最大最大值。它适用于已经以零为中心或稀疏数据的数据。

以下是如何使用上一个示例中的玩具数据与此缩放器的方法:

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. ,  1. ],
       [ 1. ,  0. ,  0. ],
       [ 0. ,  1. , -0.5]])
>>> X_test = np.array([[ -3., -1.,  4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. ,  2. ]])
>>> max_abs_scaler.scale_
array([2.,  1.,  2.])

6.3.1.2. 缩放稀疏数据#

中心化稀疏数据会破坏数据中的稀疏性结构，因此很少是明智的做法。然而，缩放稀疏输入可能是有意义的，特别是当特征处于不同尺度时。

MaxAbsScaler 专门设计用于缩放稀疏数据，是推荐的方法。 然而，StandardScaler 可以接受 scipy.sparse 矩阵作为输入，只要显式传递 with_mean=False 给构造函数。否则会引发 ValueError ，因为静默中心化会破坏稀疏性并经常无意中分配大量内存导致执行崩溃。 RobustScaler 不能拟合稀疏输入，但你可以对稀疏输入使用 transform 方法。

请注意，缩放器接受压缩稀疏行和压缩稀疏列格式（参见 scipy.sparse.csr_matrix 和 scipy.sparse.csc_matrix ）。任何其他稀疏输入将被**转换为压缩稀疏行表示**。为了避免不必要的内存复制，建议在上游选择 CSR 或 CSC 表示。

最后，如果预期的中心化数据足够小，显式地使用稀疏矩阵的 toarray 方法将输入转换为数组是另一种选择。

6.3.1.3. 使用异常值缩放数据#

如果你的数据包含许多异常值，使用数据的均值和方差进行缩放可能效果不佳。在这些情况下，你可以使用 RobustScaler 作为替代方案。它使用更稳健的估计来确定数据的中心和范围。

#参考资料

关于数据中心化和缩放重要性的进一步讨论，请参阅此常见问题解答： 我应该对数据进行归一化/标准化/重缩放吗？

#缩放与白化

有时仅独立地中心化和缩放特征是不够的，因为下游模型可能会进一步假设特征之间的线性独立性。

为了解决这个问题，你可以使用带有 whiten=True 的 PCA 来进一步去除特征间的线性相关性。

6.3.1.4. 中心化核矩阵#

如果你有一个核矩阵，核 \(K\) 计算特征空间（可能是隐式的）中由函数 \(\phi(\cdot)\) 定义的点积，一个 KernelCenterer 可以转换核矩阵，使其包含由 \(\phi\) 定义的特征空间中的内积，然后移除该空间中的均值。换句话说，KernelCenterer 计算与核相关的中心化 Gram 矩阵。 正定核 \(K\) 。

#数学表达式

现在我们已经有了直觉，可以看一下数学表达式。设 \(K\) 是一个形状为 (n_samples, n_samples) 的核矩阵， 在 fit 步骤中从形状为 (n_samples, n_features) 的数据矩阵 \(X\) 计算得到。\(K\) 定义为

\[K(X, X) = \phi(X) . \phi(X)^{T}\]

\(\phi(X)\) 是将 \(X\) 映射到希尔伯特空间的函数。一个中心化的核 \(\tilde{K}\) 定义为：

\[\tilde{K}(X, X) = \tilde{\phi}(X) . \tilde{\phi}(X)^{T}\]

其中 \(\tilde{\phi}(X)\) 是从希尔伯特空间中中心化 \(\phi(X)\) 得到的结果。

因此，可以通过使用函数 \(\phi(\cdot)\) 映射 \(X\) 并在新空间中中心化数据来计算 \(\tilde{K}\) 。然而， 核函数通常被使用是因为它们允许一些代数计算，这些计算避免了显式地使用 \(\phi(\cdot)\) 进行映射。实际上， 可以隐式地进行中心化，如 [Scholkopf1998] 中的附录 B 所示：

\[\tilde{K} = K - 1_{\text{n}_{samples}} K - K 1_{\text{n}_{samples}} + 1_{\text{n}_{samples}} K 1_{\text{n}_{samples}}\]

\(1_{\text{n}_{samples}}\) 是一个形状为 (n_samples, n_samples) 的矩阵，其中所有元素都等于 \(\frac{1}{\text{n}_{samples}}\) 。 在 transform 步骤中，核变为 \(K_{test}(X, Y)\) ，定义为：

\[K_{test}(X, Y) = \phi(Y) . \phi(X)^{T}\]

\(Y\) 是形状为 (n_samples_test, n_features) 的测试数据集，因此 \(K_{test}\) 的形状为 (n_samples_test, n_samples) 。 在这种情况下，中心化 \(K_{test}\) 的方式为：

\[\tilde{K}_{test}(X, Y) = K_{test} - 1'_{\text{n}_{samples}} K - K_{test} 1_{\text{n}_{samples}} + 1'_{\text{n}_{samples}} K 1_{\text{n}_{samples}}\]

\(1'_{\text{n}_{samples}}\) 是一个形状为 (n_samples_test, n_samples) 的矩阵，其中所有元素都等于

\(\frac{1}{\text{n}_{samples}}\) .

参考文献

[Scholkopf1998]

B. Schölkopf, A. Smola, and K.R. Müller, “非线性成分分析作为核特征值问题。” 神经计算 10.5 (1998): 1299-1319.

6.3.2. 非线性变换#

有两种类型的变换可用：分位数变换和幂变换。分位数变换和幂变换都是基于特征的单调变换，因此保留了各特征值的秩。

分位数变换将所有特征置于相同的期望分布中，基于公式 \(G^{-1}(F(X))\) ，其中 \(F\) 是特征的累积分布函数，\(G^{-1}\) 是期望输出分布 \(G\) 的分位数函数。这个公式利用了以下两个事实：(i) 如果 \(X\) 是一个具有连续累积分布函数 \(F\) 的随机变量，那么 \(F(X)\) 在 \([0,1]\) 上均匀分布；(ii) 如果 \(U\) 是一个在 \([0,1]\) 上均匀分布的随机变量，那么 \(G^{-1}(U)\) 具有分布 \(G\) 。通过执行秩变换，分位数变换平滑了不寻常的分布，并且受异常值的影响小于缩放方法。然而，它确实扭曲了特征内和特征间的相关性和距离。

幂变换是一族参数变换，旨在将数据从任何分布映射到尽可能接近高斯分布。

6.3.2.1. 映射到均匀分布#

QuantileTransformer 提供了一种非参数变换，将数据映射到值在 0 和 1 之间的均匀分布:

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split

>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]) 
array([ 4.3,  5.1,  5.8,  6.5,  7.9])

此特征对应于以厘米为单位的萼片长度。一旦应用了分位数变换，这些地标点就会接近之前定义的百分位数:

>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.00... ,  0.24...,  0.49...,  0.73...,  0.99... ])

这可以在具有类似评论的独立测试集上得到确认:

>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
... 
array([ 4.4  ,  5.125,  5.75 ,  6.175,  7.3  ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.01...,  0.25...,  0.46...,  0.60... ,  0.94...])

6.3.2.2. 映射到高斯分布#

在许多建模场景中，数据集中的特征的正态性是可取的。幂变换是一组参数化的单调变换，旨在将数据从任何分布映射到尽可能接近高斯分布，以稳定方差并最小化偏度。

PowerTransformer 目前提供了两种幂变换方法，Yeo-Johnson 变换和 Box-Cox 变换。

#Yeo-Johnson 变换
\[ \begin{align}\begin{aligned}\begin{split}x_i^{(\lambda)} = \begin{cases} [(x_i + 1)^\lambda - 1] / \lambda & \text{if } \lambda \neq 0, x_i \geq 0, \\[8pt] \ln{(x_i + 1)} & \text{if } \lambda = 0, x_i \geq 0 \\[8pt] -[(-x_i + 1)^{2 - \lambda} - 1] / (2 - \lambda) & \text{if } \lambda \neq 2, x_i < 0, \\[8pt]\end{split}\\- \ln (- x_i + 1) & \text{如果 } \lambda = 2, x_i < 0 \end{cases}\end{aligned}\end{align} \]
#Box-Cox 变换
\[\begin{split}x_i^{(\lambda)} = \begin{cases} \dfrac{x_i^\lambda - 1}{\lambda} & \text{如果 } \lambda \neq 0, \\[8pt] \ln{(x_i)} & \text{如果 } \lambda = 0, \end{cases}\end{split}\]

Box-Cox 变换只能应用于严格正数的数据。在这两种方法中，变换由 \(\lambda\) 参数化，该参数通过最大似然估计确定。以下是使用 Box-Cox 将来自对数正态分布的样本映射到正态分布的示例:

>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
      [0.94..., 1.60..., 0.38...],
      [1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49...,  0.17..., -0.15...],
      [-0.05...,  0.58..., -0.57...],
      [ 0.69..., -0.84...,  0.10...]])

虽然上述示例将 standardize 选项设置为 False ，但 PowerTransformer 默认会对变换后的输出应用零均值、单位方差归一化。

以下是 Box-Cox 和 Yeo-Johnson 应用于各种概率分布的示例。请注意，当应用于某些分布时，幂变换可以获得非常类似高斯分布的结果，但在其他分布上则效果不佳。这突显了在变换前后可视化数据的重要性。

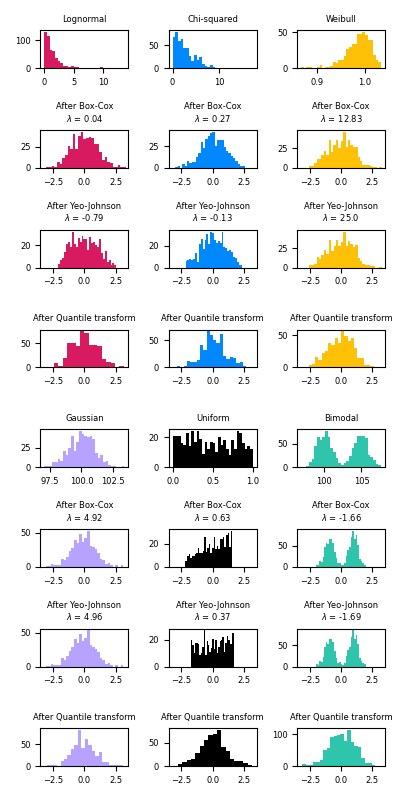
../_images/sphx_glr_plot_map_data_to_normal_001.png

还可以使用 QuantileTransformer 通过设置 output_distribution='normal' 将数据映射到正态分布。使用之前对鸢尾花数据集的示例:

>>> quantile_transformer = preprocessing.QuantileTransformer(
...     output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
       [4.4, 2.2, 1.1, 0.1],
       [4.4, 2.2, 1.2, 0.1],
       ...,
       [7.7, 4.1, 6.7, 2.5],
       [7.7, 4.2, 6.7, 2.5],
       [7.9, 4.4, 6.9, 2.5]])

因此，输入的中位数变成了输出的均值，并以0为中心。正态分布的输出被裁剪，使得输入的最小值和最大值——分别对应于1e-7和1 - 1e-7分位数——在变换下不会变成无穷大。

6.3.3. 归一化#

归一化 是将 单个样本缩放到具有单位范数 的过程。如果你计划使用二次形式（如点积或其他核函数）来量化任何样本对之间的相似性，这个过程可能是有用的。

这一假设是 向量空间模型 的基础，常用于文本分类和聚类上下文中。

函数 normalize 提供了一种快速简便的方法来对单个类数组数据集执行此操作，可以使用 l1 、 l2 或 max 范数:

 >>> X = [[ 1., -1.,  2.],
 ...      [ 2.,  0.,  0.],
 ...      [ 0.,  1., -1.]]
 >>> X_normalized = preprocessing.normalize(X, norm='l2')

 >>> X_normalized
 array([[ 0.40..., -0.40...,  0.81...],
        [ 1.  ...,  0.  ...,  0.  ...],
        [ 0.  ...,  0.70..., -0.70...]])

``preprocessing`` 模块进一步提供了一个实用类 :class:`Normalizer` ，它使用 ``Transformer`` API 实现了相同的操作（尽管在这种情况下 ``fit`` 方法是无用的：该类是无状态的，因为此操作独立处理样本）。

因此，该类适用于 Pipeline 的早期步骤:

>>> normalizer = preprocessing.Normalizer().fit(X)  # fit does nothing
>>> normalizer

Normalizer()

The normalizer instance can then be used on sample vectors as any transformer:

>>> normalizer.transform(X)
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

>>> normalizer.transform([[-1.,  1., 0.]])
array([[-0.70...,  0.70...,  0.  ...]])

Note: L2 normalization is also known as spatial sign preprocessing.

#Sparse input

normalize and Normalizer accept both dense array-like and sparse matrices from scipy.sparse as input.

For sparse input the data is converted to the Compressed Sparse Rows representation (see scipy.sparse.csr_matrix ) before being fed to efficient Cython routines. To avoid unnecessary memory copies, it is recommended to choose the CSR representation upstream.

6.3.4. Encoding categorical features#

Often features are not given as continuous values but categorical. For example a person could have features ["male", "female"] ,

["from Europe", "from US", "from Asia"] , ["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"] .

Such features can be efficiently coded as integers, for instance

["male", "from US", "uses Internet Explorer"] could be expressed as [0, 1, 3] while ["female", "from Asia", "uses Chrome"] would be [1, 2, 1] .

To convert categorical features to such integer codes, we can use the OrdinalEncoder . This estimator transforms each categorical feature to one new feature of integers (0 to n_categories - 1):

>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])

这种整数表示法虽然可以用于某些情况，但不能直接用于所有scikit-learn估计器，因为这些估计器期望连续输入，并且会将类别解释为有序的，而这通常不是我们想要的（例如，浏览器集合的顺序是任意指定的）。

默认情况下，OrdinalEncoder 也会传递由 np.nan 指示的缺失值。

>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male'], ['female'], [np.nan], ['female']]
>>> enc.fit_transform(X)
array([[ 1.],
       [ 0.],
       [nan],
       [ 0.]])

OrdinalEncoder 提供了一个参数 encoded_missing_value ，用于编码缺失值，而无需创建管道并使用 SimpleImputer 。

>>> enc = preprocessing.OrdinalEncoder(encoded_missing_value=-1)
>>> X = [['male'], ['female'], [np.nan], ['female']]
>>> enc.fit_transform(X)
array([[ 1.],
       [ 0.],
       [-1.],
       [ 0.]])

上述处理等同于以下管道:

>>> from sklearn.pipeline import Pipeline
>>> from sklearn.impute import SimpleImputer
>>> enc = Pipeline(steps=[
...     ("encoder", preprocessing.OrdinalEncoder()),
...     ("imputer", SimpleImputer(strategy="constant", fill_value=-1)),
... ])
>>> enc.fit_transform(X)
array([[ 1.],
       [ 0.],
       [-1.],
       [ 0.]])

另一种将分类特征转换为可用于scikit-learn估计器的特征的方法是使用K中的一个，也称为独热编码或哑编码。 这种类型的编码可以通过 OneHotEncoder 获得，它将每个具有 n_categories 可能值的分类特征转换为 n_categories 个二进制特征，其中一个为1，其余为0。

继续上面的例子:

>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]

>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
...                ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
       [0., 1., 1., 0., 0., 1.]])

默认情况下，每个特征可以取的值会自动从数据集中推断出来，并且可以在 categories_ 属性中找到:

>>> enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]

可以使用参数 categories 显式指定这些值。在我们的数据集中，有两种性别、四个可能的大陆和四种网络浏览器:

>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # 注意，对于第2个和第3个特征，存在缺失的分类值
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
                          ['from Africa', 'from Asia', 'from Europe',
                           'from US'],
                          ['uses Chrome', 'uses Firefox', 'uses IE',
                           'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])

如果有可能训练数据中存在缺失的分类特征，通常最好指定 handle_unknown='infrequent_if_exist' ，而不是像上面那样手动设置 categories 。当指定 handle_unknown='infrequent_if_exist' 并且在转换过程中遇到未知类别时，不会引发错误。

已提出但由此特征产生的一热编码列将全为零或被视为不频繁类别（如果启用）。 ( handle_unknown='infrequent_if_exist' 仅支持一热编码):

>>> enc = preprocessing.OneHotEncoder(handle_unknown='infrequent_if_exist')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='infrequent_if_exist')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])

也可以通过使用 drop 参数将每一列编码为 n_categories - 1 列，而不是 n_categories 列。 此参数允许用户为每个特征指定要删除的类别。这在某些分类器中避免输入矩阵的共线性很有用。 例如，在使用非正则化回归（LinearRegression ）时， 共线性会导致协方差矩阵不可逆:

>>> X = [['male', 'from US', 'uses Safari'],
...      ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object),
 array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
       [0., 0., 0.]])

可能只想为具有2个类别的特征删除两个列中的一个。在这种情况下，可以设置参数 drop='if_binary' 。

>>> X = [['male', 'US', 'Safari'],
...      ['female', 'Europe', 'Firefox'],
...      ['female', 'Asia', 'Chrome']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary').fit(X)
>>> drop_enc.categories_
[array([‘female’, ‘male’], dtype=object), array([‘Asia’, ‘Europe’, ‘US’], dtype=object),

array([‘Chrome’, ‘Firefox’, ‘Safari’], dtype=object)]

>>> drop_enc.transform(X).toarray()
array([[1., 0., 0., 1., 0., 0., 1.],
       [0., 0., 1., 0., 0., 1., 0.],
       [0., 1., 0., 0., 1., 0., 0.]])

在转换后的 X 中，第一列是具有 “male”/”female” 类别的特征的编码，而其余 6 列是分别具有 3 个类别的两个特征的编码。

当 handle_unknown='ignore' 且 drop 不为 None 时，未知类别将被编码为全零:

>>> drop_enc = preprocessing.OneHotEncoder(drop='first',
...                                        handle_unknown='ignore').fit(X)
>>> X_test = [['unknown', 'America', 'IE']]
>>> drop_enc.transform(X_test).toarray()
array([[0., 0., 0., 0., 0.]])

在转换过程中， X_test 中的所有类别都是未知的，将被映射为全零。这意味着未知类别将具有与被删除类别相同的映射。 :meth :OneHotEncoder.inverse_transform 将把全零映射到被删除的类别（如果删除了一个类别）或 None （如果未删除类别）:

>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary', sparse_output=False,
...                                        handle_unknown='ignore').fit(X)
>>> X_test = [['unknown', 'America', 'IE']]
>>> X_trans = drop_enc.transform(X_test)
>>> X_trans
array([[0., 0., 0., 0., 0., 0., 0.]])
>>> drop_enc.inverse_transform(X_trans)
array([['female', None, None]], dtype=object)
#支持包含缺失值的分类特征

OneHotEncoder 通过将缺失值视为一个额外的类别来支持包含缺失值的分类特征:

>>> X = [['male', 'Safari'],
...      ['female', None],
...      [np.nan, 'Firefox']]


>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['female', 'male', nan], dtype=object),
array(['Firefox', 'Safari', None], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0., 1., 0.],
      [1., 0., 0., 0., 0., 1.],
      [0., 0., 1., 1., 0., 0.]])

如果一个特征同时包含 np.nan 和 None ，它们将被视为不同的类别:

>>> X = [['Safari'], [None], [np.nan], ['Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['Firefox', 'Safari', None, nan], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0.],
      [0., 0., 1., 0.],
      [0., 0., 0., 1.],
      [1., 0., 0., 0.]])

有关以字典形式表示的分类特征，请参阅 从字典加载特征 。

6.3.4.1. 不常见类别#

OneHotEncoder 和 OrdinalEncoder 支持将不常见的类别聚合为每个特征的单个输出。启用不常见类别聚合的参数是 min_frequency 和 max_categories 。

  1. min_frequency 是一个大于或等于 1 的整数，或者是一个在区间 (0.0, 1.0) 内的浮点数。如果 min_frequency 是整数，则基数小于 min_frequency 的类别将被视为不常见。如果 min_frequency 是浮点数，则基数小于样本总数这一比例的类别将被视为不常见。默认值为 1，这意味着每个类别都单独编码。

  2. max_categories 是 None 或任何大于 1 的整数。此参数为每个输入特征设置输出特征数量的上限。 max_categories 包括聚合不常见类别的特征。

在以下使用 OrdinalEncoder 的示例中，类别 'dog' 和 'snake' 被视为不频繁出现的类别:

>>> X = np.array([['dog'] * 5 + ['cat'] * 20 + ['rabbit'] * 10 +
...               ['snake'] * 3], dtype=object).T
>>> enc = preprocessing.OrdinalEncoder(min_frequency=6).fit(X)
>>> enc.infrequent_categories_
[array(['dog', 'snake'], dtype=object)]
>>> enc.transform(np.array([['dog'], ['cat'], ['rabbit'], ['snake']]))
array([[2.],
       [0.],
       [1.],
       [2.]])

OrdinalEncoder 的 max_categories 参数**不**考虑缺失或未知的类别。设置 unknown_value 或 encoded_missing_value 为整数将使唯一整数码的数量增加一个。这可能导致最多 max_categories + 2 个整数码。在以下示例中，”a” 和 “d” 被视为不频繁出现的类别并被归入同一类别，”b” 和 “c” 各自为单独的类别，未知值被编码为 3，缺失值被编码为 4。

>>> X_train = np.array(
...     [["a"] * 5 + ["b"] * 20 + ["c"] * 10 + ["d"] * 3 + [np.nan]],
...     dtype=object).T
>>> enc = preprocessing.OrdinalEncoder(
...     handle_unknown="use_encoded_value", unknown_value=3,
...     max_categories=3, encoded_missing_value=4)
>>> _ = enc.fit(X_train)
>>> X_test = np.array([["a"], ["b"], ["c"], ["d"], ["e"], [np.nan]], dtype=object)
>>> enc.transform(X_test)
array([[2.],
       [0.],
       [1.],
       [2.],
       [3.],
       [4.]])

类似地， OneHotEncoder 也可以配置为将不频繁出现的类别归并在一起:

>>> enc = preprocessing.OneHotEncoder(min_frequency=6, sparse_output=False).fit(X)
>>> enc.infrequent_categories_
[array(['dog', 'snake'], dtype=object)]
>>> enc.transform(np.array([['dog'], ['cat'], ['rabbit'], ['snake']]))
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

通过将 handle_unknown 设置为 'infrequent_if_exist' ，未知的类别将被视为不频繁的类别:

>>> enc = preprocessing.OneHotEncoder(
...    handle_unknown='infrequent_if_exist', sparse_output=False, min_frequency=6)
>>> enc = enc.fit(X)
>>> enc.transform(np.array([['dragon']]))
array([[0., 0., 1.]])

:meth :OneHotEncoder.get_feature_names_out 使用 ‘infrequent’ 作为不频繁特征的名称:

>>> enc.get_feature_names_out()
array(['x0_cat', 'x0_rabbit', 'x0_infrequent_sklearn'], dtype=object)

当 'handle_unknown' 设置为 'infrequent_if_exist' 并且在转换过程中遇到未知类别时：

  1. 如果未配置不频繁类别支持或在训练期间没有不频繁类别，则该特征的独热编码列将全为零。在逆转换中，未知类别将表示为 None 。

  2. 如果在训练期间存在不频繁类别，则未知类别将被视为不频繁类别。在逆转换中，将使用 ‘infrequent_sklearn’ 来表示不频繁类别。

不频繁类别也可以通过 max_categories 进行配置。在以下示例中，我们设置 max_categories=2 以限制输出中的特征数量。这将导致除 'cat' 类别外的所有类别被视为不频繁类别，从而产生两个特征，一个用于 'cat' ，一个用于不频繁类别（即所有其他类别）:

>>> enc = preprocessing.OneHotEncoder(max_categories=2, sparse_output=False)
>>> enc = enc.fit(X)
>>> enc.transform([['dog'], ['cat'], ['rabbit'], ['snake']])
array([[0., 1.],
       [1., 0.],
       [0., 1.],
       [0., 1.]])

如果 max_categories 和 min_frequency 都是非默认值，则首先根据 min_frequency 选择类别，然后保留 max_categories 个类别。在以下示例中， min_frequency=4 考虑 仅 snake 出现频率较低，但 max_categories=3 迫使 dog 也变为 低频:

>>> enc = preprocessing.OneHotEncoder(min_frequency=4, max_categories=3, sparse_output=False)
>>> enc = enc.fit(X)
>>> enc.transform([['dog'], ['cat'], ['rabbit'], ['snake']])
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

如果在 max_categories 的截断点上存在相同基数的低频类别，那么将根据词典顺序选择前 max_categories 个。在以下示例中，”b”、”c” 和 “d” 具有相同的基数，并且由于 max_categories=2 ，”b” 和 “c” 被视为低频，因为它们的词典顺序较高。

>>> X = np.asarray([["a"] * 20 + ["b"] * 10 + ["c"] * 10 + ["d"] * 10], dtype=object).T
>>> enc = preprocessing.OneHotEncoder(max_categories=3).fit(X)
>>> enc.infrequent_categories_
[array(['b', 'c'], dtype=object)]

6.3.4.2. 目标编码器#

TargetEncoder 使用目标均值条件化分类特征进行无序类别（即名义类别）的编码 [PAR] [MIC]。这种编码方案对于具有高基数的分类特征非常有用，其中独热编码会膨胀特征空间，使得下游模型的处理成本更高。高基数类别的一个经典例子是基于位置的，如邮政编码或地区。

#二分类目标

对于二分类目标，目标编码由以下公式给出：

\[S_i = \lambda_i\frac{n_{iY}}{n_i} + (1 - \lambda_i)\frac{n_Y}{n}\]

其中 \(S_i\) 是类别 \(i\) 的编码，\(n_{iY}\) 是具有 \(Y=1\) 和类别 \(i\) 的观测数量，\(n_i\) 是具有类别 \(i\) 的观测数量，\(n_Y\) 是具有 \(Y=1\) 的观测数量。

具有 \(Y=1\) 的观测值，\(n\) 是观测值的数量，而 \(\lambda_i\) 是类别 \(i\) 的收缩因子。收缩因子由以下公式给出：

\[\lambda_i = \frac{n_i}{m + n_i}\]

其中 \(m\) 是一个平滑因子，通过 TargetEncoder 中的 smooth 参数控制。较大的平滑因子会在全局均值上施加更多权重。当 smooth="auto" 时，平滑因子计算为经验贝叶斯估计：\(m=\sigma_i^2/\tau^2\) ，其中 \(\sigma_i^2\) 是类别 \(i\) 中 y 的方差，而 \(\tau^2\) 是 y 的全局方差。

#多类分类目标

对于多类分类目标，公式类似于二元分类：

\[S_{ij} = \lambda_i\frac{n_{iY_j}}{n_i} + (1 - \lambda_i)\frac{n_{Y_j}}{n}\]

其中 \(S_{ij}\) 是类别 \(i\) 和类别 \(j\) 的编码，\(n_{iY_j}\) 是具有 \(Y=j\) 和类别 \(i\) 的观测值数量，\(n_i\) 是具有类别 \(i\) 的观测值数量，\(n_{Y_j}\) 是具有 \(Y=j\) 的观测值数量，\(n\) 是观测值的总数量，而 \(\lambda_i\) 是类别 \(i\) 的收缩因子。

#连续目标

对于连续目标，公式类似于二元分类：

\[S_i = \lambda_i\frac{\sum_{k\in L_i}Y_k}{n_i} + (1 - \lambda_i)\frac{\sum_{k=1}^{n}Y_k}{n}\]

其中 \(L_i\) 是具有类别 \(i\) 的观测值集合，而 \(n_i\) 是具有类别 \(i\) 的观测值数量。

fit_transform 内部依赖于 交叉拟合 方案，以防止目标信息泄漏到训练时表示中，特别是对于非信息性的高基数分类变量，并有助于防止下游模型对虚假相关性过度拟合。 相关性。请注意，因此， fit(X, y).transform(X) 并不等于 fit_transform(X, y) 。在 fit_transform 方法中，训练数据被分成 k 折（由 cv 参数决定），每一折使用其他 k-1 折学到的编码进行编码。下面的图示展示了在默认 cv=5 情况下的 fit_transform 方法中的 交叉拟合 方案：

../_images/target_encoder_cross_validation.svg

fit_transform 方法还使用整个训练集学习了一个“完整数据”编码。这个编码在 fit_transform 方法中从未使用，但被保存到 encodings_ 属性中，以供调用 transform 方法时使用。请注意，在 交叉拟合 方案中为每一折学到的编码不会保存到属性中。

fit 方法**不**使用任何 交叉拟合 方案，而是在整个训练集上学习一个编码，这个编码用于在 transform 方法中对类别进行编码。这个编码与在 fit_transform 方法中学习的“完整数据”编码相同。

Note

TargetEncoder 考虑缺失值，例如 np.nan 或 None ，将其视为另一个类别，并像其他类别一样对其进行编码。在 fit 过程中未见过的类别使用目标均值进行编码，即 target_mean_ 。

示例

参考文献

6.3.5. 离散化#

（也称为量化或分箱）提供了一种将连续特征划分为离散值的方法。某些具有连续特征的数据集可能会从离散化中受益，因为离散化可以将连续属性的数据集转换为仅包含名义属性的数据集。

独热编码的离散化特征可以使模型更具表达性，同时保持可解释性。例如，使用离散化器进行预处理可以向线性模型引入非线性。有关更多高级可能性，特别是平滑的可能性，请参见下面的 生成多项式特征 。

6.3.5.1. K-bins 离散化#

KBinsDiscretizer 将特征离散化为 k 个箱:

>>> X = np.array([[ -3., 5., 15 ],
...               [  0., 6., 14 ],
...               [  6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)

默认情况下，输出是独热编码为稀疏矩阵（参见 Encoding categorical features ），这可以通过 encode 参数进行配置。对于每个特征，箱边缘在 fit 期间计算，并与箱的数量一起定义区间。因此，对于当前示例，这些区间定义为：

  • 特征 1: \({[-\infty, -1), [-1, 2), [2, \infty)}\)

  • 特征 2: \({[-\infty, 5), [5, \infty)}\)

  • 特征 3: \({[-\infty, 14), [14, \infty)}\)

基于这些箱区间， X 被转换如下:

>>> est.transform(X)                      
array([[ 0., 1., 1.],
       [ 1., 1., 1.],
       [ 2., 0., 0.]])

生成的数据集包含可以进一步用于 Pipeline 的有序属性。

离散化类似于为连续数据构建直方图。然而，直方图关注于计算落入特定区间的特征，而离散化关注于将特征值分配给这些区间。

KBinsDiscretizer 实现了不同的分箱策略，可以通过 strategy 参数进行选择。’uniform’ 策略使用恒定宽度的区间。’quantile’ 策略使用分位数值，以使每个特征中的区间具有相同数量的样本。’kmeans’ 策略基于在每个特征上独立执行的 k-means 聚类过程定义区间。

请注意，可以通过将定义离散化策略的可调用对象传递给 FunctionTransformer 来指定自定义区间。例如，我们可以使用 Pandas 函数 pandas.cut

>>> import pandas as pd
>>> import numpy as np
>>> from sklearn import preprocessing
>>>
>>> bins = [0, 1, 13, 20, 60, np.inf]
>>> labels = ['婴儿', '儿童', '青少年', '成人', '老年公民']
>>> transformer = preprocessing.FunctionTransformer(
...     pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
... )
>>> X = np.array([0.2, 2, 15, 25, 97])
>>> transformer.fit_transform(X)
['婴儿', '儿童', '青少年', '成人', '老年公民']
类别 (5, 对象): ['婴儿' < '儿童' < '青少年' < '成人' < '老年公民']

示例

6.3.5.2. 特征二值化#

特征二值化 是将 数值特征通过阈值处理转换为布尔值 的过程。这对于下游的

假设输入数据遵循多元 伯努利分布 的概率估计器。例如，这是 BernoulliRBM 的情况。

在文本处理社区中，即使归一化计数（即词频）或 TF-IDF 值特征在实践中通常表现稍好，使用二进制特征值（可能是为了简化概率推理）也很常见。

至于 Normalizer ，实用类 Binarizer 旨在用于 Pipeline 的早期阶段。 fit 方法不做任何事情，因为每个样本都是独立处理的:

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]

>>> binarizer = preprocessing.Binarizer().fit(X)  # fit does nothing
>>> binarizer
Binarizer()

>>> binarizer.transform(X)
array([[1., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.]])

可以调整二值化器的阈值:

>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 0., 0.]])

至于 Normalizer 类，预处理模块提供了一个伴随函数 binarize ，用于不需要转换器 API 的情况。

请注意，当 k = 2 且分箱边缘位于 threshold 值时，Binarizer 类似于 KBinsDiscretizer 。

6.3.6. 缺失值的插补#

插补缺失值的工具在 缺失值的插补 中讨论。

6.3.7. 生成多项式特征#

通常，通过考虑输入数据的非线性特征来增加模型的复杂性是有用的。我们展示了两种基于多项式的方法：第一种使用纯多项式，第二种使用样条，即分段多项式。

6.3.7.1. 多项式特征#

一个简单且常用的方法是使用多项式特征，它可以获得特征的高阶项和交互项。它在 PolynomialFeatures 中实现:

>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

X 的特征已从 \((X_1, X_2)\) 转换为 \((1, X_1, X_2, X_1^2, X_1X_2, X_2^2)\) 。

在某些情况下，只需要特征之间的交互项，可以通过设置 interaction_only=True 来实现:

>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   2.,   0.,   0.,   2.,   0.],
       [  1.,   3.,   4.,   5.,  12.,  15.,  20.,  60.],
       [  1.,   6.,   7.,   8.,  42.,  48.,  56., 336.]])

X 的特征已从 \((X_1, X_2, X_3)\) 转换为 \((1, X_1, X_2, X_3, X_1X_2, X_1X_3, X_2X_3, X_1X_2X_3)\) 。

请注意，多项式特征在 kernel methods 中隐式使用。

内核方法 （例如，SVC ，

KernelPCA ）在使用多项式 核函数 时。

参见 多项式和样条插值 用于使用创建的多项式特征进行岭回归。

6.3.7.2. 样条变换器#

另一种添加非线性项的方法是使用 SplineTransformer 为每个特征生成样条基函数，而不是纯多项式。样条是分段多项式，由其多项式度和节点位置参数化。SplineTransformer 实现了 B-样条基，参见下面的参考文献。

Note

SplineTransformer 对每个特征单独处理，即不会给出交互项。

样条相对于多项式的一些优点包括：

  • B-样条在保持固定低度（通常为 3）并适度调整节点数量时非常灵活和稳健。多项式需要更高的度数，这导致了下一点。

  • B-样条在边界处没有多项式那样的振荡行为（度数越高，情况越糟）。这被称为 龙格现象 。

  • B-样条提供了良好的边界外推选项，即超出拟合值范围的选项。请查看 extrapolation 选项。

  • B-样条生成的特征矩阵具有带状结构。对于单个特征，每行仅包含 degree + 1 个非零元素，这些元素连续出现并且都是正的。这导致了一个具有良好数值特性的矩阵，例如低条件数，与多项式矩阵（称为 范德蒙矩阵 ）形成鲜明对比。

低条件数对于线性模型的稳定算法非常重要。

以下代码片段展示了样条线的实际应用:

>>> import numpy as np
>>> from sklearn.preprocessing import SplineTransformer
>>> X = np.arange(5).reshape(5, 1)
>>> X
array([[0],
       [1],
       [2],
       [3],
       [4]])
>>> spline = SplineTransformer(degree=2, n_knots=3)
>>> spline.fit_transform(X)
array([[0.5  , 0.5  , 0.   , 0.   ],
       [0.125, 0.75 , 0.125, 0.   ],
       [0.   , 0.5  , 0.5  , 0.   ],
       [0.   , 0.125, 0.75 , 0.125],
       [0.   , 0.   , 0.5  , 0.5  ]])

由于 X 已排序，可以很容易地看到带状矩阵输出。对于 degree=2 ，只有中间三条对角线是非零的。度数越高，样条线重叠越多。

有趣的是， degree=0 的 SplineTransformer 与 encode='onehot-dense' 和 n_bins = n_knots - 1 的 KBinsDiscretizer 相同，如果 knots = strategy 。

示例

#参考文献

6.3.8. 自定义转换器#

通常，您会希望将现有的 Python 函数转换为转换器，以协助数据清理或处理。您可以使用 FunctionTransformer 从任意函数实现一个转换器。例如，要在管道中构建一个应用对数变换的转换器，请执行以下操作:

>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> # Since FunctionTransformer is no-op during fit, we can call transform directly
>>> transformer.transform(X)
array([[0.        , 0.69314718],
       [1.09861229, 1.38629436]])

你可以通过设置 check_inverse=True 并在调用 transform 之前调用 fit 来确保 func 和 inverse_func 是互为逆函数。请注意，会引发一个警告，可以使用 filterwarnings 将其转换为错误:

>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
...                         category=UserWarning, append=False)

有关使用 FunctionTransformer 从文本数据中提取特征的完整代码示例，请参见 具有异构数据源的列转换器 和 时间相关特征工程 。

On this page
Show Source