Note
Go to the end to download the full example code. or to run this example in your browser via Binder
比较不同缩放器对含有异常值的数据的影响#
California Housing dataset 的特征0(街区的中位收入)和特征5(平均房屋入住率)具有非常不同的尺度,并且包含一些非常大的异常值。这两个特征导致数据可视化困难,更重要的是,它们可能会降低许多机器学习算法的预测性能。未缩放的数据还可能会减慢甚至阻止许多基于梯度的估计器的收敛。
实际上,许多估计器的设计假设每个特征的取值接近零,或者更重要的是,所有特征的变化尺度相当。特别是,基于度量和基于梯度的估计器通常假设数据大致标准化(特征居中且方差为单位)。一个显著的例外是基于决策树的估计器,它们对数据的任意缩放具有鲁棒性。
此示例使用不同的缩放器、变换器和归一化器将数据带入预定义范围内。
缩放器是线性(或更准确地说是仿射)变换器,它们在估计用于平移和缩放每个特征的参数的方式上有所不同。
QuantileTransformer 提供非线性变换,其中边缘异常值和内围值之间的距离被缩小。
PowerTransformer 提供非线性变换,其中数据被映射到正态分布以稳定方差并最小化偏度。
与之前的变换不同,归一化是指每个样本的变换,而不是每个特征的变换。
以下代码有点冗长,可以直接跳到结果分析_。
# 作者:scikit-learn 开发者
# SPDX-License-Identifier:BSD-3-Clause
import matplotlib as mpl
import numpy as np
from matplotlib import cm
from matplotlib import pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import (
MaxAbsScaler,
MinMaxScaler,
Normalizer,
PowerTransformer,
QuantileTransformer,
RobustScaler,
StandardScaler,
minmax_scale,
)
dataset = fetch_california_housing()
X_full, y_full = dataset.data, dataset.target
feature_names = dataset.feature_names
feature_mapping = {
"MedInc": "Median income in block",
"HouseAge": "Median house age in block",
"AveRooms": "Average number of rooms",
"AveBedrms": "Average number of bedrooms",
"Population": "Block population",
"AveOccup": "Average house occupancy",
"Latitude": "House block latitude",
"Longitude": "House block longitude",
}
# 仅选择两个特征以简化可视化。
# 特征 MedInc 具有长尾分布。
# 特征 AveOccup 有一些但非常大的异常值。
features = ["MedInc", "AveOccup"]
features_idx = [feature_names.index(feature) for feature in features]
X = X_full[:, features_idx]
distributions = [
("Unscaled data", X),
("Data after standard scaling", StandardScaler().fit_transform(X)),
("Data after min-max scaling", MinMaxScaler().fit_transform(X)),
("Data after max-abs scaling", MaxAbsScaler().fit_transform(X)),
(
"Data after robust scaling",
RobustScaler(quantile_range=(25, 75)).fit_transform(X),
),
(
"Data after power transformation (Yeo-Johnson)",
PowerTransformer(method="yeo-johnson").fit_transform(X),
),
(
"Data after power transformation (Box-Cox)",
PowerTransformer(method="box-cox").fit_transform(X),
),
(
"Data after quantile transformation (uniform pdf)",
QuantileTransformer(
output_distribution="uniform", random_state=42
).fit_transform(X),
),
(
"Data after quantile transformation (gaussian pdf)",
QuantileTransformer(
output_distribution="normal", random_state=42
).fit_transform(X),
),
("Data after sample-wise L2 normalizing", Normalizer().fit_transform(X)),
]
# 将输出缩放到0和1之间用于颜色条
y = minmax_scale(y_full)
# 等离子体在matplotlib 1.5以下版本中不存在
cmap = getattr(cm, "plasma_r", cm.hot_r)
def create_axes(title, figsize=(16, 6)):
fig = plt.figure(figsize=figsize)
fig.suptitle(title)
# 定义第一个图的轴
left, width = 0.1, 0.22
bottom, height = 0.1, 0.7
bottom_h = height + 0.15
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter = plt.axes(rect_scatter)
ax_histx = plt.axes(rect_histx)
ax_histy = plt.axes(rect_histy)
# 定义放大图的轴
left = width + left + 0.2
left_h = left + width + 0.02
rect_scatter = [left, bottom, width, height]
rect_histx = [left, bottom_h, width, 0.1]
rect_histy = [left_h, bottom, 0.05, height]
ax_scatter_zoom = plt.axes(rect_scatter)
ax_histx_zoom = plt.axes(rect_histx)
ax_histy_zoom = plt.axes(rect_histy)
# 定义颜色条的轴
left, width = width + left + 0.13, 0.01
rect_colorbar = [left, bottom, width, height]
ax_colorbar = plt.axes(rect_colorbar)
return (
(ax_scatter, ax_histy, ax_histx),
(ax_scatter_zoom, ax_histy_zoom, ax_histx_zoom),
ax_colorbar,
)
def plot_distribution(axes, X, y, hist_nbins=50, title="", x0_label="", x1_label=""):
ax, hist_X1, hist_X0 = axes
ax.set_title(title)
ax.set_xlabel(x0_label)
ax.set_ylabel(x1_label)
# 散点图
colors = cmap(y)
ax.scatter(X[:, 0], X[:, 1], alpha=0.5, marker="o", s=5, lw=0, c=colors)
# 移除顶部和右侧的脊柱以提高美观度
# 制作良好的坐标轴布局
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.get_xaxis().tick_bottom()
ax.get_yaxis().tick_left()
ax.spines["left"].set_position(("outward", 10))
ax.spines["bottom"].set_position(("outward", 10))
# X1轴的直方图(特征5)
hist_X1.set_ylim(ax.get_ylim())
hist_X1.hist(
X[:, 1], bins=hist_nbins, orientation="horizontal", color="grey", ec="grey"
)
hist_X1.axis("off")
# X0轴(特征0)的直方图
hist_X0.set_xlim(ax.get_xlim())
hist_X0.hist(
X[:, 0], bins=hist_nbins, orientation="vertical", color="grey", ec="grey"
)
hist_X0.axis("off")
将为每个缩放器/归一化器/转换器显示两个图。左图将显示整个数据集的散点图,而右图将排除极端值,仅考虑99%的数据集,排除边缘异常值。此外,散点图的两侧将显示每个特征的边缘分布。
def make_plot(item_idx):
title, X = distributions[item_idx]
ax_zoom_out, ax_zoom_in, ax_colorbar = create_axes(title)
axarr = (ax_zoom_out, ax_zoom_in)
plot_distribution(
axarr[0],
X,
y,
hist_nbins=200,
x0_label=feature_mapping[features[0]],
x1_label=feature_mapping[features[1]],
title="Full data",
)
# zoom-in
zoom_in_percentile_range = (0, 99)
cutoffs_X0 = np.percentile(X[:, 0], zoom_in_percentile_range)
cutoffs_X1 = np.percentile(X[:, 1], zoom_in_percentile_range)
non_outliers_mask = np.all(X > [cutoffs_X0[0], cutoffs_X1[0]], axis=1) & np.all(
X < [cutoffs_X0[1], cutoffs_X1[1]], axis=1
)
plot_distribution(
axarr[1],
X[non_outliers_mask],
y[non_outliers_mask],
hist_nbins=50,
x0_label=feature_mapping[features[0]],
x1_label=feature_mapping[features[1]],
title="Zoom-in",
)
norm = mpl.colors.Normalize(y_full.min(), y_full.max())
mpl.colorbar.ColorbarBase(
ax_colorbar,
cmap=cmap,
norm=norm,
orientation="vertical",
label="Color mapping for values of y",
)
原始数据#
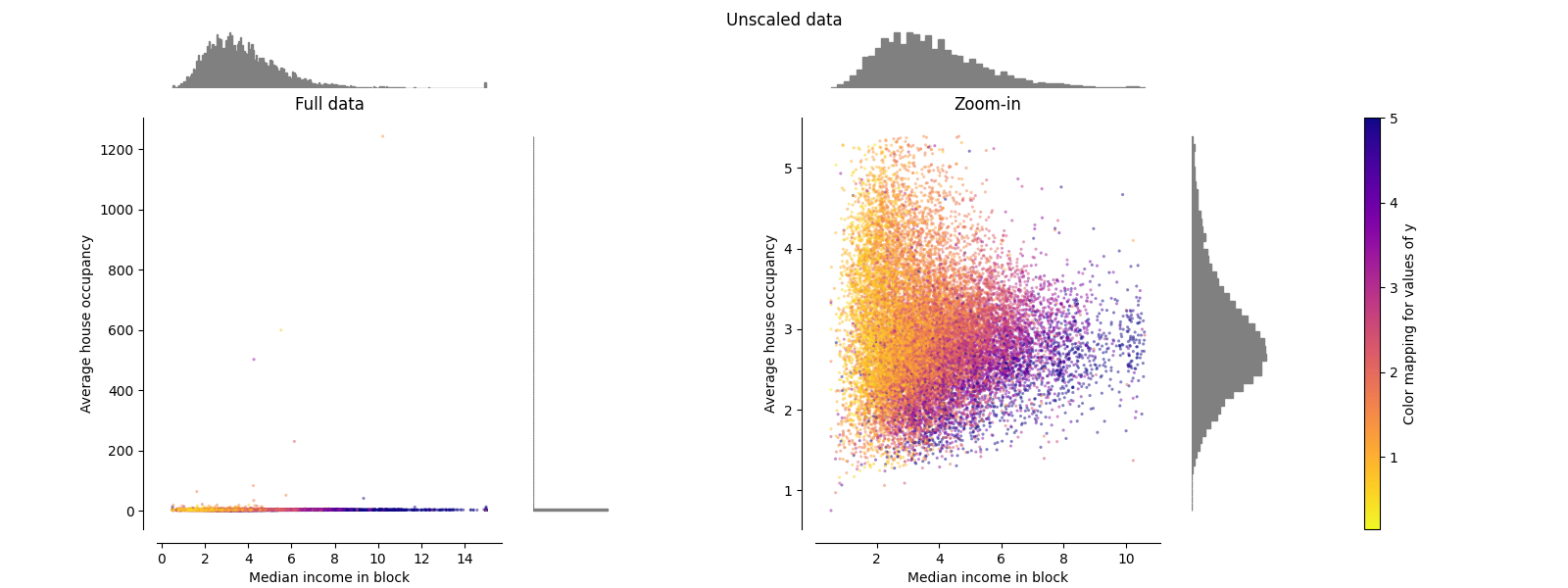
每个转换都会绘制图表,显示两个转换后的特征,左图显示整个数据集,右图放大显示没有边缘异常值的数据集。大多数样本被压缩到特定范围内,中位收入为 [0, 10],平均房屋入住率为 [0, 6]。请注意,有一些边缘异常值(某些街区的平均入住率超过 1200)。因此,根据具体应用,特定的预处理可能非常有益。以下内容展示了在存在边缘异常值的情况下,这些预处理方法的一些见解和行为。
make_plot(0)
标准化缩放器#
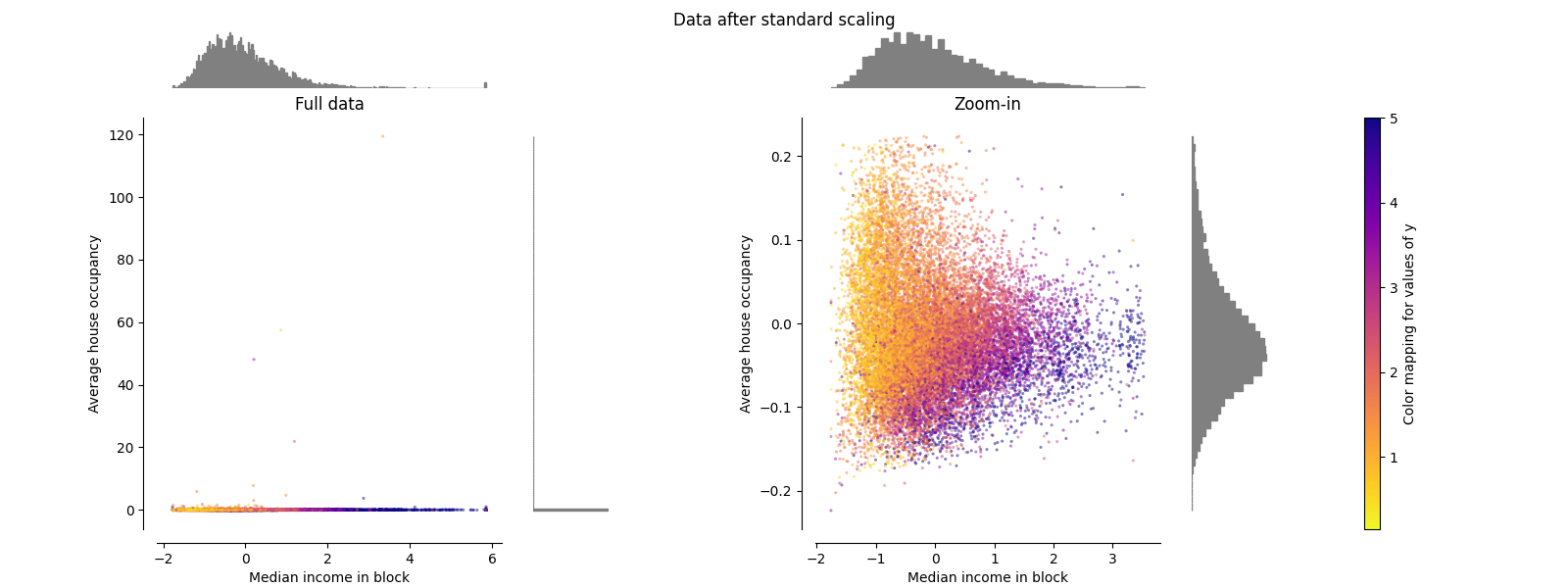
StandardScaler 移除均值并将数据缩放到单位方差。缩放会缩小特征值的范围,如下图左侧所示。
然而,计算经验均值和标准差时,离群值会产生影响。特别需要注意的是,由于每个特征的离群值具有不同的幅度,转换后数据在每个特征上的分布非常不同:对于转换后的中位收入特征,大部分数据位于 [-2, 4] 范围内,而对于转换后的平均房屋占用率特征,相同的数据被压缩在较小的 [-0.2, 0.2] 范围内。
因此,StandardScaler 在存在异常值的情况下无法保证特征尺度的平衡。
make_plot(1)
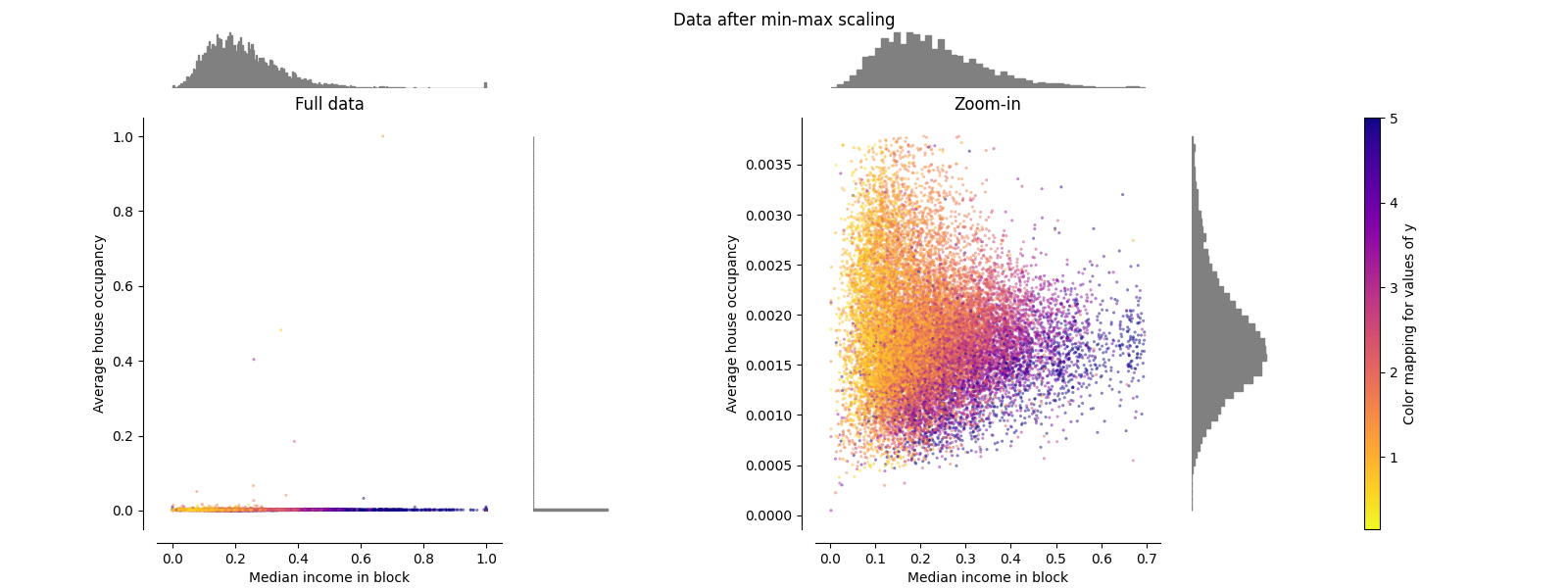
最小最大缩放器#
MinMaxScaler 重新调整数据集,使所有特征值都在 [0, 1] 范围内,如下图右侧面板所示。然而,这种缩放会将所有内围值压缩到 [0, 0.005] 的狭窄范围内,用于转换后的平均房屋占用率。
StandardScaler 和 MinMaxScaler 对异常值的存在都非常敏感。
make_plot(2)
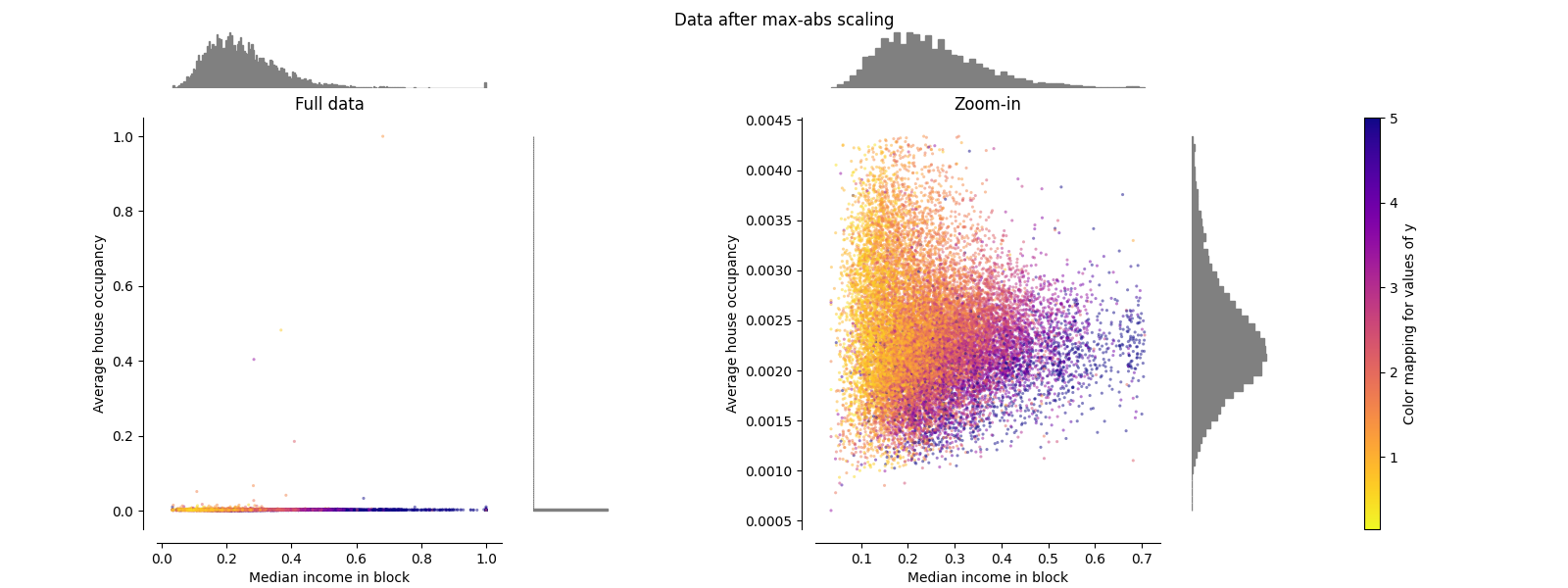
最大绝对值缩放器#
MaxAbsScaler 类似于 MinMaxScaler ,不同之处在于值会根据是否存在负值或正值而映射到不同的范围。如果仅存在正值,范围是 [0, 1]。如果仅存在负值,范围是 [-1, 0]。如果同时存在负值和正值,范围是 [-1, 1]。在仅有正值的数据上,MinMaxScaler 和 MaxAbsScaler 的表现相似。因此,MaxAbsScaler 也会受到大异常值的影响。
make_plot(3)
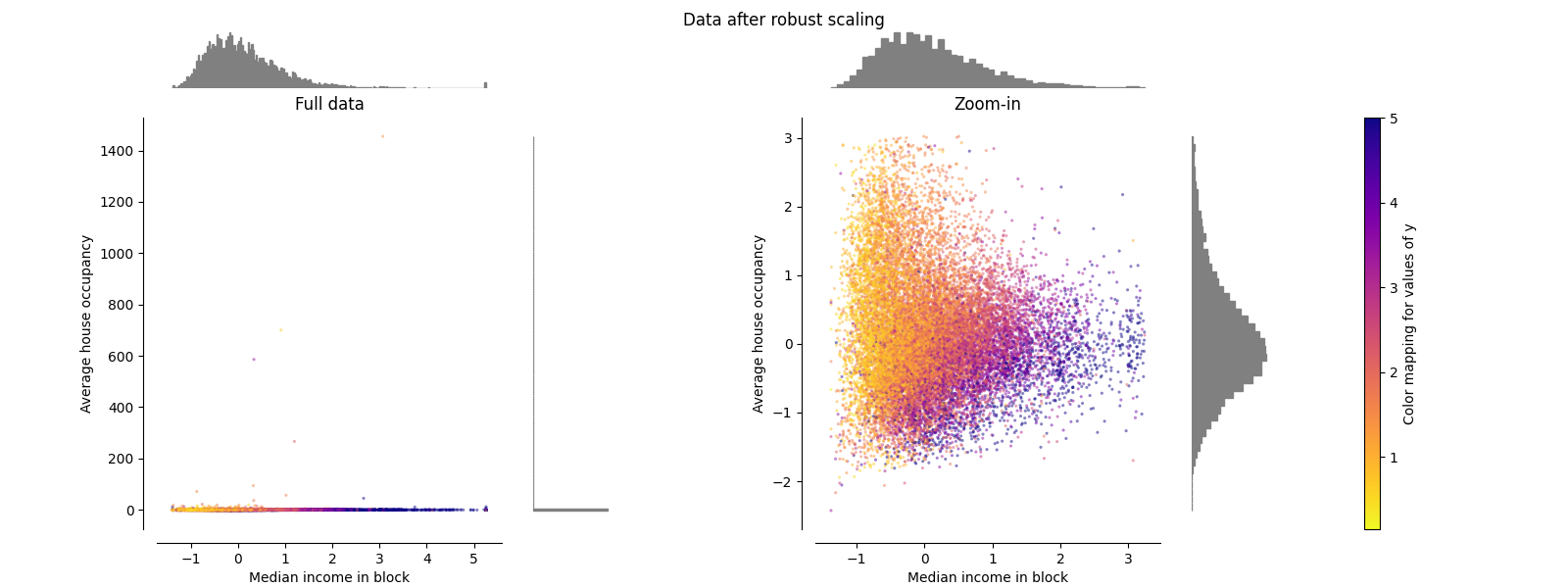
鲁棒缩放器#
与之前的缩放器不同,RobustScaler 的中心化和缩放统计基于百分位数,因此不会受到少量非常大的边缘异常值的影响。因此,转换后的特征值范围比之前的缩放器更大,更重要的是,大致相似:对于两个特征,大多数转换后的值位于缩放图中所示的 [-2, 3] 范围内。请注意,异常值本身在转换后的数据中仍然存在。如果需要单独的异常值剪裁,则需要进行非线性转换(见下文)。
make_plot(4)
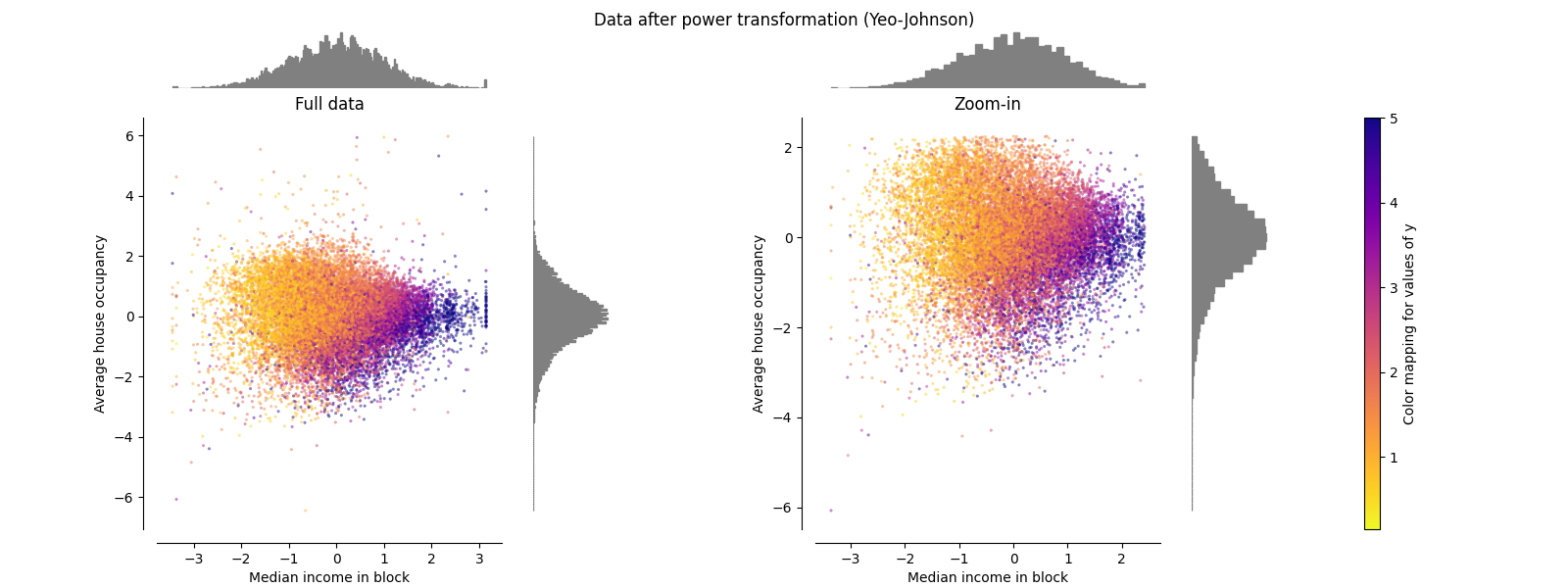
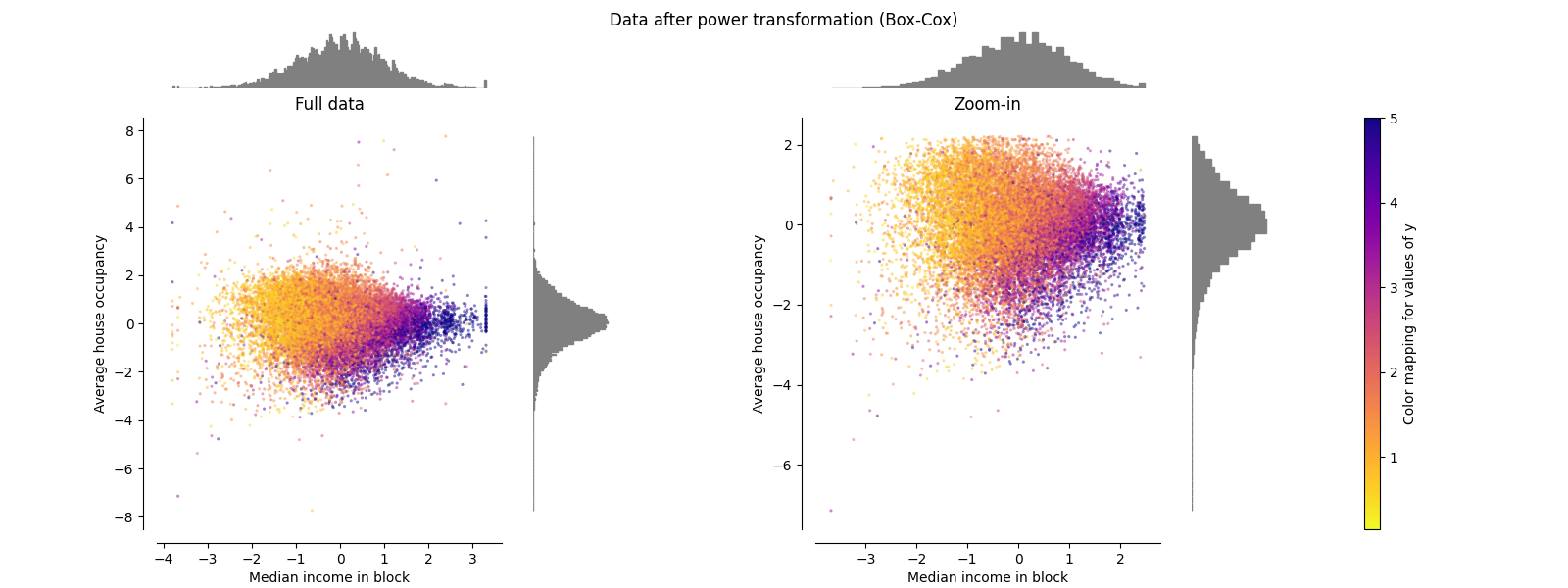
电力变压器#
PowerTransformer 对每个特征应用幂变换,使数据更接近高斯分布,以稳定方差并最小化偏度。目前支持 Yeo-Johnson 和 Box-Cox 变换,并且在这两种方法中通过最大似然估计确定最佳缩放因子。默认情况下,PowerTransformer 应用零均值、单位方差归一化。请注意,Box-Cox 只能应用于严格正的数据。收入和平均房屋占用率恰好是严格正的,但如果存在负值,则优先使用 Yeo-Johnson 变换。
make_plot(5)
make_plot(6)
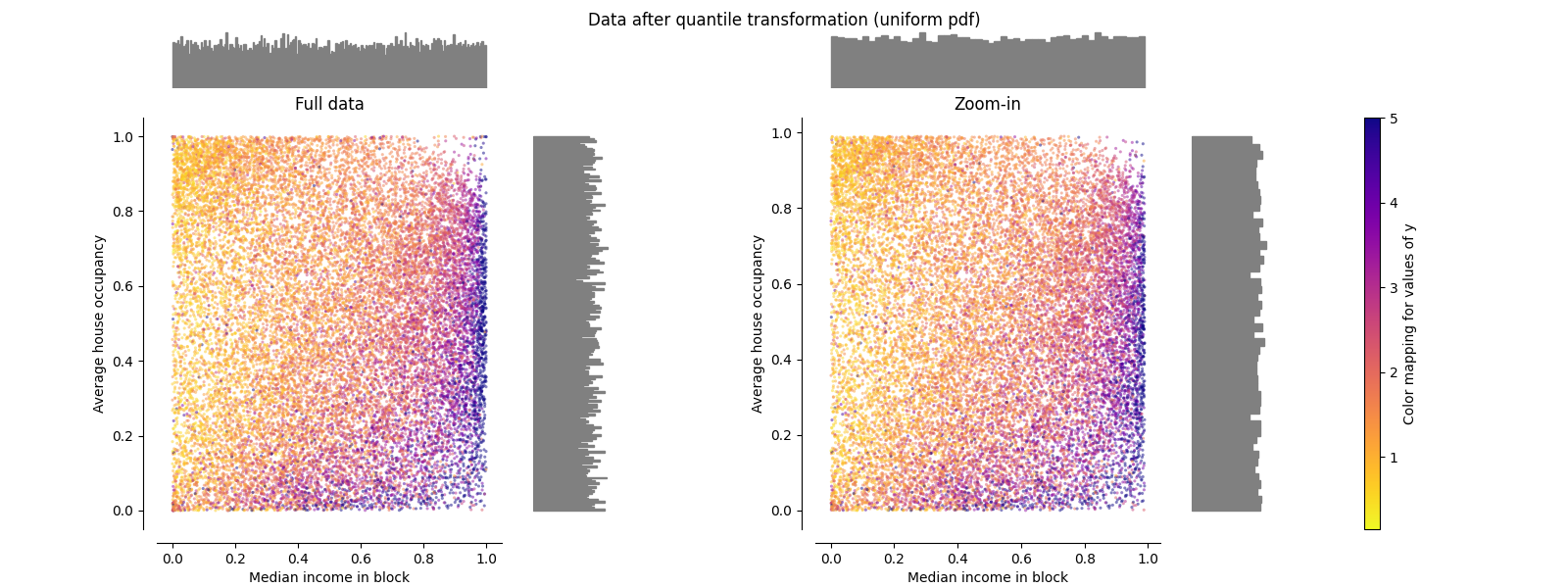
分位数变换器(均匀输出)
QuantileTransformer 应用非线性变换,使得每个特征的概率密度函数将被映射到均匀或高斯分布。在这种情况下,所有数据,包括异常值,都将被映射到范围为 [0, 1] 的均匀分布,使得异常值与内点无法区分。
RobustScaler 和 QuantileTransformer 对异常值具有鲁棒性,因为在训练集中添加或删除异常值将产生大致相同的转换。但与 RobustScaler 相反,QuantileTransformer 还会通过将任何异常值设置为预先定义的范围边界(0 和 1)来自动折叠它们。这可能会导致极值的饱和伪影。
make_plot(7)
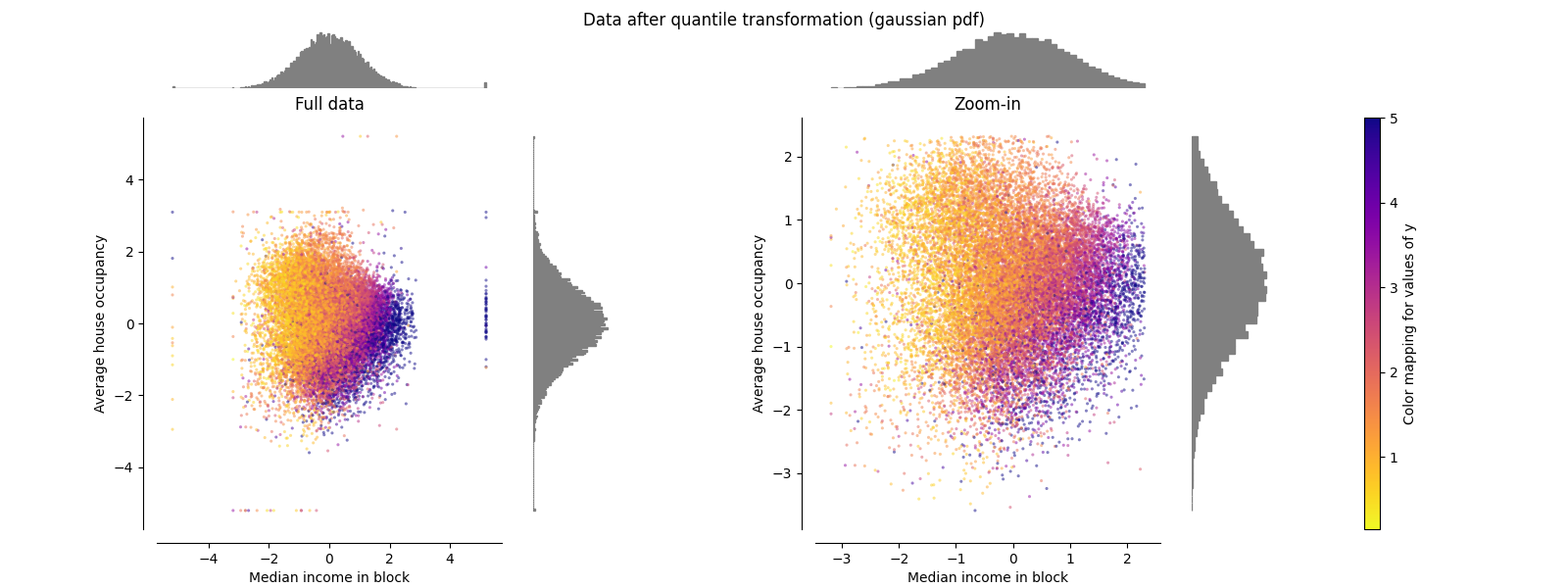
分位数变换器(高斯输出)#
要映射到高斯分布,请设置参数 output_distribution='normal' 。
make_plot(8)
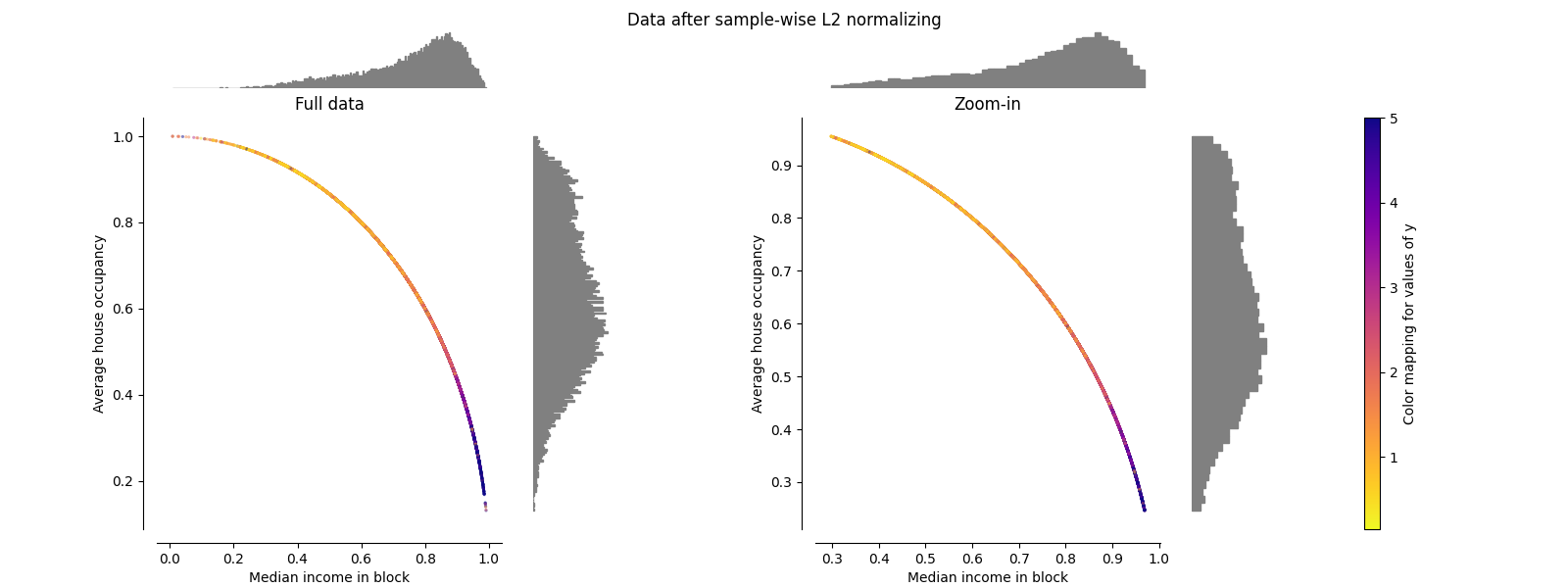
Normalizer#
Normalizer 会将每个样本的向量重新缩放为单位范数,而不考虑样本的分布。在下面的两个图中可以看到,所有样本都被映射到单位圆上。在我们的例子中,所选的两个特征只有正值;因此,转换后的数据仅位于正象限。如果某些原始特征包含正负值的混合情况,则不会出现这种情况。
make_plot(9)
plt.show()
Total running time of the script: (0 minutes 3.591 seconds)
Related examples