基于L1的稀疏信号模型

本示例比较了三种基于L1的回归模型在一个由稀疏且相关特征生成的合成信号上的表现，这些信号进一步被加性高斯噪声所破坏：

• Lasso ;

• 自动相关性确定 ;

• 弹性网络 .

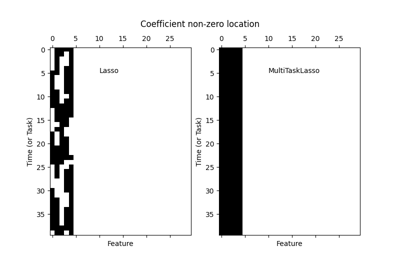
已知当数据维度增加时，Lasso估计值趋近于模型选择估计值，前提是无关变量与相关变量的相关性不太高。在存在相关特征的情况下，Lasso本身无法选择正确的稀疏模式 [1]。

在这里，我们比较了这三种模型在以下方面的表现：\(R^2\) 得分、拟合时间以及估计系数的稀疏性，并与真实值进行对比。

# Author: Arturo Amor <david-arturo.amor-quiroz@inria.fr>

生成合成数据集

我们生成一个样本数量少于特征总数的数据集。这会导致一个欠定系统，即解不是唯一的，因此我们不能单独应用普通最小二乘法。正则化在目标函数中引入一个惩罚项，这会修改优化问题，并有助于缓解系统的欠定性质。

目标 y 是正弦信号的交替符号线性组合。 X 中的 100 个频率中只有最低的 10 个被用来生成 y ，其余的特征没有信息量。这导致了一个高维稀疏特征空间，其中需要一定程度的 l1 惩罚。

import numpy as np

rng = np.random.RandomState(0)
n_samples, n_features, n_informative = 50, 100, 10
time_step = np.linspace(-2, 2, n_samples)
freqs = 2 * np.pi * np.sort(rng.rand(n_features)) / 0.01
X = np.zeros((n_samples, n_features))

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step)

idx = np.arange(n_features)
true_coef = (-1) ** idx * np.exp(-idx / 10)
true_coef[n_informative:] = 0  # sparsify coef
y = np.dot(X, true_coef)

一些信息特征具有接近的频率，从而引发（反）相关性。

freqs[:n_informative]

array([ 2.9502547 , 11.8059798 , 12.63394388, 12.70359377, 24.62241605,
       37.84077985, 40.30506066, 44.63327171, 54.74495357, 59.02456369])

使用 numpy.random.random_sample 引入随机相位，并向特征和目标添加一些高斯噪声（由 numpy.random.normal 实现）。

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step + 2 * (rng.random_sample() - 0.5))
    X[:, i] += 0.2 * rng.normal(0, 1, n_samples)

y += 0.2 * rng.normal(0, 1, n_samples)

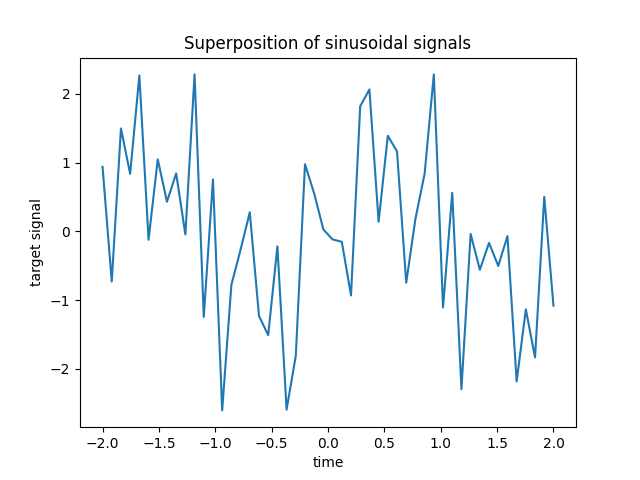
例如，从监测某些环境变量的传感器节点可以获得这种稀疏、噪声和相关的特征，因为它们通常根据其位置（空间相关性）记录相似的值。 我们可以可视化目标。

import matplotlib.pyplot as plt

plt.plot(time_step, y)
plt.ylabel("target signal")
plt.xlabel("time")
_ = plt.title("Superposition of sinusoidal signals")

我们将数据分为训练集和测试集以简化操作。实际上，应该使用 TimeSeriesSplit 交叉验证来估计测试分数的方差。这里我们设置 shuffle="False" ，因为在处理具有时间关系的数据时，不能使用在测试数据之后的训练数据。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, shuffle=False)

在下文中，我们计算了三个基于 l1 模型的拟合优度 \(R^2\) 得分和拟合时间。然后我们绘制了一个图表，将估计系数的稀疏性与真实系数进行比较，最后我们分析了之前的结果。

Lasso

在这个示例中，我们演示了一个具有固定正则化参数 alpha 的 Lasso 。在实际应用中，应该通过将 TimeSeriesSplit 交叉验证策略传递给 LassoCV 来选择最优参数 alpha 。为了使示例简单且执行速度快，我们在这里直接设置了 alpha 的最优值。

from time import time

from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score

t0 = time()
lasso = Lasso(alpha=0.14).fit(X_train, y_train)
print(f"Lasso fit done in {(time() - t0):.3f}s")

y_pred_lasso = lasso.predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(f"Lasso r^2 on test data : {r2_score_lasso:.3f}")

Lasso fit done in 0.001s
Lasso r^2 on test data : 0.480

自动相关性确定 (ARD)

ARD回归是Lasso的贝叶斯版本。如果需要，它可以为所有参数（包括误差方差）生成区间估计。当信号具有高斯噪声时，它是一个合适的选择。请参阅示例 比较线性贝叶斯回归器 ，以比较 ARDRegression 和 BayesianRidge 回归器。

from sklearn.linear_model import ARDRegression

t0 = time()
ard = ARDRegression().fit(X_train, y_train)
print(f"ARD fit done in {(time() - t0):.3f}s")

y_pred_ard = ard.predict(X_test)
r2_score_ard = r2_score(y_test, y_pred_ard)
print(f"ARD r^2 on test data : {r2_score_ard:.3f}")

ARD fit done in 0.018s
ARD r^2 on test data : 0.543

ElasticNet

ElasticNet 是 Lasso 和 Ridge 之间的中间地带，因为它结合了 L1 和 L2 惩罚。正则化的程度由两个超参数 l1_ratio 和 alpha 控制。当 l1_ratio = 0 时，惩罚是纯 L2，模型等同于 Ridge 。类似地， l1_ratio = 1 是纯 L1 惩罚，模型等同于 Lasso 。对于 0 < l1_ratio < 1 ，惩罚是 L1 和 L2 的组合。

正如之前所做的，我们使用固定的 alpha 和 l1_ratio 值来训练模型。为了选择它们的最优值，我们使用了 ElasticNetCV ，这里没有展示以保持示例的简洁。

from sklearn.linear_model import ElasticNet

t0 = time()
enet = ElasticNet(alpha=0.08, l1_ratio=0.5).fit(X_train, y_train)
print(f"ElasticNet fit done in {(time() - t0):.3f}s")

y_pred_enet = enet.predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(f"ElasticNet r^2 on test data : {r2_score_enet:.3f}")

ElasticNet fit done in 0.001s
ElasticNet r^2 on test data : 0.636

结果的绘图和分析

在本节中，我们使用热图来可视化各线性模型的真实和估计系数的稀疏性。

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib.colors import SymLogNorm

df = pd.DataFrame(
    {
        "True coefficients": true_coef,
        "Lasso": lasso.coef_,
        "ARDRegression": ard.coef_,
        "ElasticNet": enet.coef_,
    }
)

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-1, vmax=1),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("linear model")
plt.xlabel("coefficients")
plt.title(
    f"Models' coefficients\nLasso $R^2$: {r2_score_lasso:.3f}, "
    f"ARD $R^2$: {r2_score_ard:.3f}, "
    f"ElasticNet $R^2$: {r2_score_enet:.3f}"
)
plt.tight_layout()

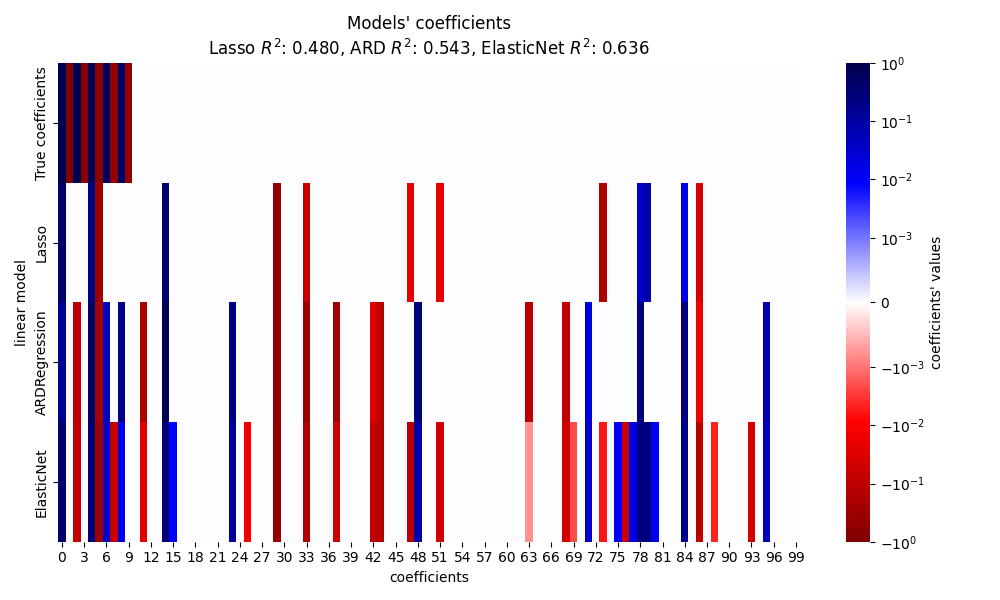
在当前示例中，ElasticNet 得到了最佳分数并捕捉到了大部分预测特征，但仍未能找到所有的真实成分。请注意，ElasticNet 和 ARDRegression 生成的模型比 Lasso 更不稀疏。

结论

Lasso 被认为能够有效地恢复稀疏数据，但在处理高度相关的特征时表现不佳。实际上，如果多个相关特征对目标有贡献，Lasso 最终只会选择其中一个。在稀疏但不相关的特征情况下，Lasso 模型会更合适。

ElasticNet 在系数上引入了一些稀疏性，并将它们的值缩小到零。因此，在存在对目标有贡献的相关特征的情况下，模型仍然能够减少它们的权重，而不将它们完全设为零。这导致模型比纯粹的 Lasso 更不稀疏，并且可能捕捉到非预测性特征。

ARDRegression 在处理高斯噪声时表现更好，但仍然无法处理相关特征，并且由于需要拟合先验分布，耗时较长。

References

[1]

“高维数据稀疏表示的Lasso型恢复” N. Meinshausen, B. Yu - 统计年鉴 2009, 第37卷, 第1期, 246-270

Related examples

稠密数据和稀疏数据上的Lasso回归

稠密数据和稀疏数据上的Lasso回归

多任务Lasso的联合特征选择

多任务Lasso的联合特征选择

Lasso 和弹性网络

Lasso 和弹性网络

使用预计算的Gram矩阵和加权样本拟合弹性网络

使用预计算的Gram矩阵和加权样本拟合弹性网络