Note
Go to the end to download the full example code. or to run this example in your browser via Binder
离散数据结构上的高斯过程#
本示例展示了如何在非固定长度特征向量形式的数据上使用高斯过程进行回归和分类任务。 这是通过使用直接作用于离散结构(如可变长度序列、树和图)的核函数来实现的。
具体来说,这里的输入变量是一些基因序列,这些序列存储为由字母 ‘A’、’T’、’C’ 和 ‘G’ 组成的可变长度字符串, 而输出变量在回归任务中是浮点数,在分类任务中是 True/False 标签。
通过在一对字符串的所有字母对上整合二元字母核,使用 R-卷积 [1] 定义基因序列之间的核。
本示例将生成三个图。
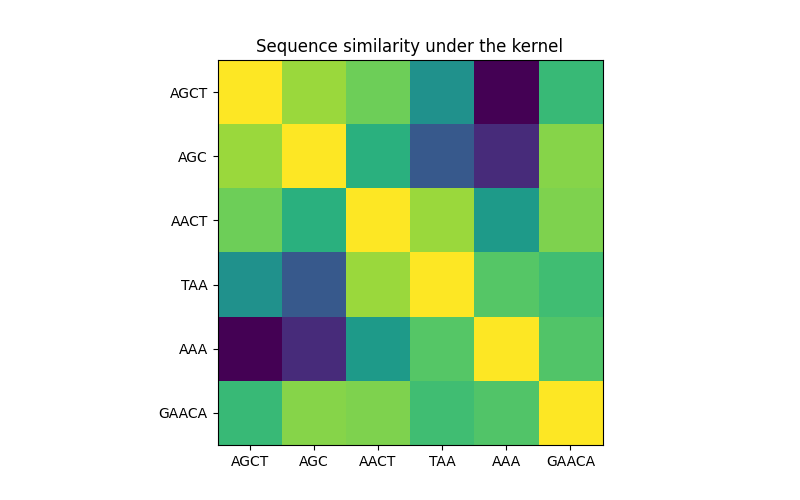
在第一个图中,我们使用颜色图可视化核的值,即序列的相似性。颜色越亮表示相似性越高。
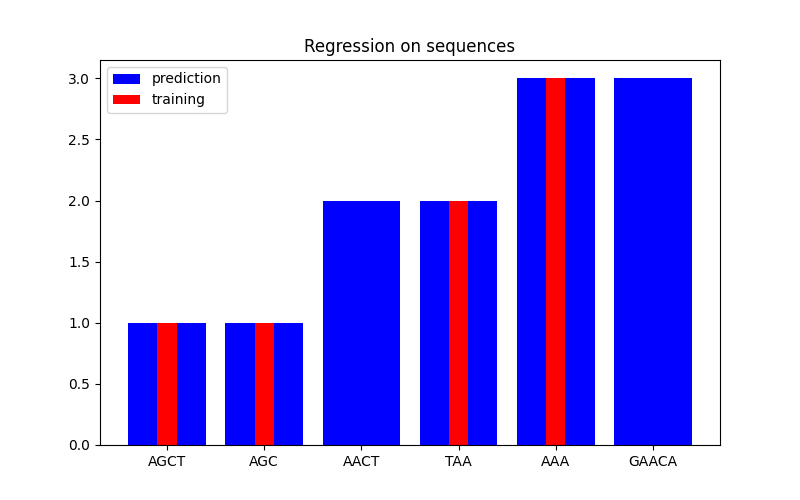
在第二个图中,我们展示了在一个包含 6 个序列的数据集上的回归结果。这里我们使用第 1、2、4 和 5 个序列作为训练集, 对第 3 和 6 个序列进行预测。
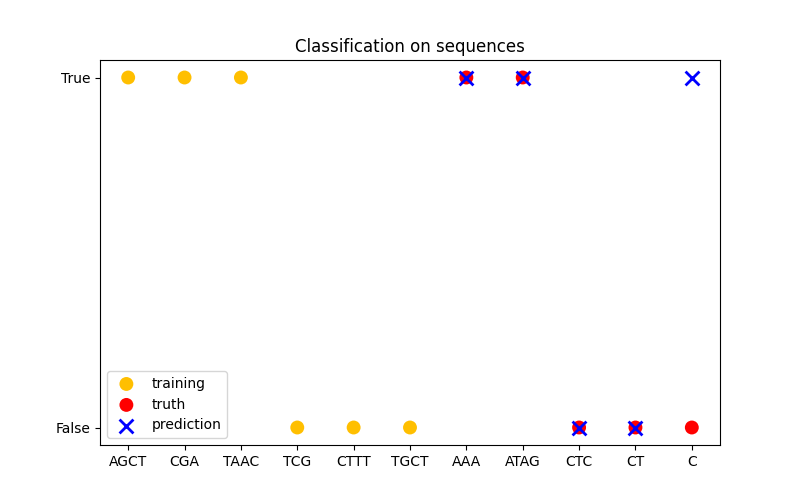
在第三个图中,我们通过在 6 个序列上进行训练并对另外 5 个序列进行预测来展示分类模型。这里的真实情况只是序列中是否至少有一个 ‘A’。 模型做出了四个正确分类,失败了一个。
import numpy as np
from sklearn.base import clone
from sklearn.gaussian_process import GaussianProcessClassifier, GaussianProcessRegressor
from sklearn.gaussian_process.kernels import GenericKernelMixin, Hyperparameter, Kernel
class SequenceKernel(GenericKernelMixin, Kernel):
"""一个用于变长序列的最小(但有效的)卷积核。"""
def __init__(self, baseline_similarity=0.5, baseline_similarity_bounds=(1e-5, 1)):
self.baseline_similarity = baseline_similarity
self.baseline_similarity_bounds = baseline_similarity_bounds
@property
def hyperparameter_baseline_similarity(self):
return Hyperparameter(
"baseline_similarity", "numeric", self.baseline_similarity_bounds
)
def _f(self, s1, s2):
"""
序列对之间的核值
"""
return sum(
[1.0 if c1 == c2 else self.baseline_similarity for c1 in s1 for c2 in s2]
)
def _g(self, s1, s2):
"""
序列对之间的核导数
"""
return sum([0.0 if c1 == c2 else 1.0 for c1 in s1 for c2 in s2])
def __call__(self, X, Y=None, eval_gradient=False):
if Y is None:
Y = X
if eval_gradient:
return (
np.array([[self._f(x, y) for y in Y] for x in X]),
np.array([[[self._g(x, y)] for y in Y] for x in X]),
)
else:
return np.array([[self._f(x, y) for y in Y] for x in X])
def diag(self, X):
return np.array([self._f(x, x) for x in X])
def is_stationary(self):
return False
def clone_with_theta(self, theta):
cloned = clone(self)
cloned.theta = theta
return cloned
kernel = SequenceKernel()
核下的序列相似性矩阵#
import matplotlib.pyplot as plt
X = np.array(["AGCT", "AGC", "AACT", "TAA", "AAA", "GAACA"])
K = kernel(X)
D = kernel.diag(X)
plt.figure(figsize=(8, 5))
plt.imshow(np.diag(D**-0.5).dot(K).dot(np.diag(D**-0.5)))
plt.xticks(np.arange(len(X)), X)
plt.yticks(np.arange(len(X)), X)
plt.title("Sequence similarity under the kernel")
plt.show()
Regression#
X = np.array(["AGCT", "AGC", "AACT", "TAA", "AAA", "GAACA"])
Y = np.array([1.0, 1.0, 2.0, 2.0, 3.0, 3.0])
training_idx = [0, 1, 3, 4]
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(X[training_idx], Y[training_idx])
plt.figure(figsize=(8, 5))
plt.bar(np.arange(len(X)), gp.predict(X), color="b", label="prediction")
plt.bar(training_idx, Y[training_idx], width=0.2, color="r", alpha=1, label="training")
plt.xticks(np.arange(len(X)), X)
plt.title("Regression on sequences")
plt.legend()
plt.show()
分类#
X_train = np.array(["AGCT", "CGA", "TAAC", "TCG", "CTTT", "TGCT"])
# 是否序列中有 'A'
Y_train = np.array([True, True, True, False, False, False])
gp = GaussianProcessClassifier(kernel)
gp.fit(X_train, Y_train)
X_test = ["AAA", "ATAG", "CTC", "CT", "C"]
Y_test = [True, True, False, False, False]
plt.figure(figsize=(8, 5))
plt.scatter(
np.arange(len(X_train)),
[1.0 if c else -1.0 for c in Y_train],
s=100,
marker="o",
edgecolor="none",
facecolor=(1, 0.75, 0),
label="training",
)
plt.scatter(
len(X_train) + np.arange(len(X_test)),
[1.0 if c else -1.0 for c in Y_test],
s=100,
marker="o",
edgecolor="none",
facecolor="r",
label="truth",
)
plt.scatter(
len(X_train) + np.arange(len(X_test)),
[1.0 if c else -1.0 for c in gp.predict(X_test)],
s=100,
marker="x",
facecolor="b",
linewidth=2,
label="prediction",
)
plt.xticks(np.arange(len(X_train) + len(X_test)), np.concatenate((X_train, X_test)))
plt.yticks([-1, 1], [False, True])
plt.title("Classification on sequences")
plt.legend()
plt.show()
/app/scikit-learn-main-origin/sklearn/gaussian_process/kernels.py:421: ConvergenceWarning:
The optimal value found for dimension 0 of parameter baseline_similarity is close to the specified lower bound 1e-05. Decreasing the bound and calling fit again may find a better value.
Total running time of the script: (0 minutes 0.106 seconds)
Related examples