Note
Go to the end to download the full example code. or to run this example in your browser via Binder
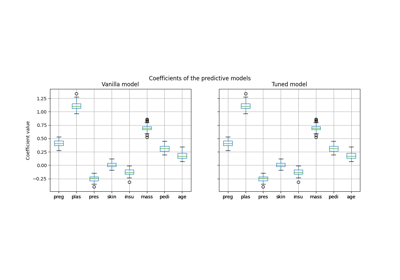
基于模型和顺序特征选择#
此示例说明并比较了两种特征选择方法:
基于特征重要性的 SelectFromModel 和
依赖于贪婪方法的 SequentialFeatureSelector 。
我们使用糖尿病数据集,该数据集包含从442名糖尿病患者收集的10个特征。
- 作者:Manoj Kumar ,
Maria Telenczuk , Nicolas Hug.
许可证: BSD 3条款
加载数据#
我们首先加载scikit-learn中提供的糖尿病数据集,并打印其描述:
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target
print(diabetes.DESCR)
.. _diabetes_dataset:
Diabetes dataset
----------------
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
**Data Set Characteristics:**
:Number of Instances: 442
:Number of Attributes: First 10 columns are numeric predictive values
:Target: Column 11 is a quantitative measure of disease progression one year after baseline
:Attribute Information:
- age age in years
- sex
- bmi body mass index
- bp average blood pressure
- s1 tc, total serum cholesterol
- s2 ldl, low-density lipoproteins
- s3 hdl, high-density lipoproteins
- s4 tch, total cholesterol / HDL
- s5 ltg, possibly log of serum triglycerides level
- s6 glu, blood sugar level
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times the square root of `n_samples` (i.e. the sum of squares of each column totals 1).
Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)
从系数中提取特征重要性#
为了了解特征的重要性,我们将使用 RidgeCV 估计器。具有最高绝对 coef_ 值的特征被认为是最重要的。我们可以直接观察系数,而不需要对它们(或数据)进行缩放,因为从上面的描述中,我们知道这些特征已经标准化。关于线性模型系数解释的更完整示例,可以参考 线性模型系数解释中的常见陷阱 。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import RidgeCV
ridge = RidgeCV(alphas=np.logspace(-6, 6, num=5)).fit(X, y)
importance = np.abs(ridge.coef_)
feature_names = np.array(diabetes.feature_names)
plt.bar(height=importance, x=feature_names)
plt.title("Feature importances via coefficients")
plt.show()
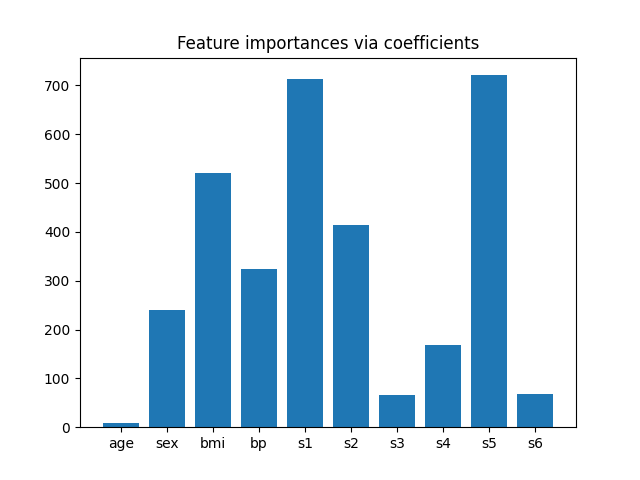
根据重要性选择特征#
现在我们希望根据系数选择两个最重要的特征。SelectFromModel 就是为此目的设计的。SelectFromModel 接受一个 threshold 参数,并将选择重要性(由系数定义)高于此阈值的特征。
由于我们只想选择两个特征,因此我们将阈值设置得略高于第三重要特征的系数。
from time import time
from sklearn.feature_selection import SelectFromModel
threshold = np.sort(importance)[-3] + 0.01
tic = time()
sfm = SelectFromModel(ridge, threshold=threshold).fit(X, y)
toc = time()
print(f"Features selected by SelectFromModel: {feature_names[sfm.get_support()]}")
print(f"Done in {toc - tic:.3f}s")
Features selected by SelectFromModel: ['s1' 's5']
Done in 0.001s
使用顺序特征选择进行特征选择#
另一种选择特征的方法是使用 SequentialFeatureSelector (SFS)。SFS 是一种贪婪的过程,在每次迭代中,我们根据交叉验证得分选择要添加到已选特征中的最佳新特征。也就是说,我们从 0 个特征开始,选择得分最高的最佳单一特征。该过程重复进行,直到我们达到所需的选定特征数量。
我们也可以反向进行(向后序列特征选择,backward SFS),即从所有特征开始,逐个贪婪地选择要移除的特征。我们在这里展示这两种方法。
from sklearn.feature_selection import SequentialFeatureSelector
tic_fwd = time()
sfs_forward = SequentialFeatureSelector(
ridge, n_features_to_select=2, direction="forward"
).fit(X, y)
toc_fwd = time()
tic_bwd = time()
sfs_backward = SequentialFeatureSelector(
ridge, n_features_to_select=2, direction="backward"
).fit(X, y)
toc_bwd = time()
print(
"Features selected by forward sequential selection: "
f"{feature_names[sfs_forward.get_support()]}"
)
print(f"Done in {toc_fwd - tic_fwd:.3f}s")
print(
"Features selected by backward sequential selection: "
f"{feature_names[sfs_backward.get_support()]}"
)
print(f"Done in {toc_bwd - tic_bwd:.3f}s")
Features selected by forward sequential selection: ['bmi' 's5']
Done in 0.073s
Features selected by backward sequential selection: ['bmi' 's5']
Done in 0.251s
有趣的是,前向选择和后向选择选择了相同的特征集。通常情况下,情况并非如此,这两种方法会导致不同的结果。
我们还注意到,SFS选择的特征与特征重要性选择的特征不同:SFS选择了 bmi 而不是 s1 。不过这听起来是合理的,因为根据系数, bmi 是第三重要的特征。考虑到SFS完全不使用系数,这一点相当显著。
最后,我们应该注意到 SelectFromModel 比 SFS 快得多。实际上,SelectFromModel 只需要拟合一次模型,而 SFS 需要在每次迭代中交叉验证许多不同的模型。然而,SFS 可以与任何模型一起使用,而 SelectFromModel 要求底层估计器具有 coef_ 属性或 feature_importances_ 属性。前向 SFS 比后向 SFS 快,因为它只需要执行 n_features_to_select = 2 次迭代,而后向 SFS 需要执行 n_features - n_features_to_select = 8 次迭代。
使用负容差值#
SequentialFeatureSelector 可以用于移除数据集中存在的特征,并返回一个较小的原始特征子集,使用 direction="backward" 和负值的 tol 。
我们首先加载乳腺癌数据集,该数据集包含30个不同的特征和569个样本。
import numpy as np
from sklearn.datasets import load_breast_cancer
breast_cancer_data = load_breast_cancer()
X, y = breast_cancer_data.data, breast_cancer_data.target
feature_names = np.array(breast_cancer_data.feature_names)
print(breast_cancer_data.DESCR)
.. _breast_cancer_dataset:
Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 569
:Number of Attributes: 30 numeric, predictive attributes and the class
:Attribute Information:
- radius (mean of distances from center to points on the perimeter)
- texture (standard deviation of gray-scale values)
- perimeter
- area
- smoothness (local variation in radius lengths)
- compactness (perimeter^2 / area - 1.0)
- concavity (severity of concave portions of the contour)
- concave points (number of concave portions of the contour)
- symmetry
- fractal dimension ("coastline approximation" - 1)
The mean, standard error, and "worst" or largest (mean of the three
worst/largest values) of these features were computed for each image,
resulting in 30 features. For instance, field 0 is Mean Radius, field
10 is Radius SE, field 20 is Worst Radius.
- class:
- WDBC-Malignant
- WDBC-Benign
:Summary Statistics:
===================================== ====== ======
Min Max
===================================== ====== ======
radius (mean): 6.981 28.11
texture (mean): 9.71 39.28
perimeter (mean): 43.79 188.5
area (mean): 143.5 2501.0
smoothness (mean): 0.053 0.163
compactness (mean): 0.019 0.345
concavity (mean): 0.0 0.427
concave points (mean): 0.0 0.201
symmetry (mean): 0.106 0.304
fractal dimension (mean): 0.05 0.097
radius (standard error): 0.112 2.873
texture (standard error): 0.36 4.885
perimeter (standard error): 0.757 21.98
area (standard error): 6.802 542.2
smoothness (standard error): 0.002 0.031
compactness (standard error): 0.002 0.135
concavity (standard error): 0.0 0.396
concave points (standard error): 0.0 0.053
symmetry (standard error): 0.008 0.079
fractal dimension (standard error): 0.001 0.03
radius (worst): 7.93 36.04
texture (worst): 12.02 49.54
perimeter (worst): 50.41 251.2
area (worst): 185.2 4254.0
smoothness (worst): 0.071 0.223
compactness (worst): 0.027 1.058
concavity (worst): 0.0 1.252
concave points (worst): 0.0 0.291
symmetry (worst): 0.156 0.664
fractal dimension (worst): 0.055 0.208
===================================== ====== ======
:Missing Attribute Values: None
:Class Distribution: 212 - Malignant, 357 - Benign
:Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian
:Donor: Nick Street
:Date: November, 1995
This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://goo.gl/U2Uwz2
Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass. They describe
characteristics of the cell nuclei present in the image.
Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree. Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.
The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].
This database is also available through the UW CS ftp server:
ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/machine-learn/WDBC/
.. dropdown:: References
- W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction
for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on
Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
San Jose, CA, 1993.
- O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and
prognosis via linear programming. Operations Research, 43(4), pages 570-577,
July-August 1995.
- W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)
163-171.
我们将使用 LogisticRegression 估计器与 SequentialFeatureSelector 进行特征选择。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
for tol in [-1e-2, -1e-3, -1e-4]:
start = time()
feature_selector = SequentialFeatureSelector(
LogisticRegression(),
n_features_to_select="auto",
direction="backward",
scoring="roc_auc",
tol=tol,
n_jobs=2,
)
model = make_pipeline(StandardScaler(), feature_selector, LogisticRegression())
model.fit(X, y)
end = time()
print(f"\ntol: {tol}")
print(f"Features selected: {feature_names[model[1].get_support()]}")
print(f"ROC AUC score: {roc_auc_score(y, model.predict_proba(X)[:, 1]):.3f}")
print(f"Done in {end - start:.3f}s")
tol: -0.01
Features selected: ['worst perimeter']
ROC AUC score: 0.975
Done in 6.445s
tol: -0.001
Features selected: ['radius error' 'fractal dimension error' 'worst texture'
'worst perimeter' 'worst concave points']
ROC AUC score: 0.997
Done in 5.932s
tol: -0.0001
Features selected: ['mean compactness' 'mean concavity' 'mean concave points' 'radius error'
'area error' 'concave points error' 'symmetry error'
'fractal dimension error' 'worst texture' 'worst perimeter' 'worst area'
'worst concave points' 'worst symmetry']
ROC AUC score: 0.998
Done in 5.406s
我们可以看到,随着 tol 的负值接近零,选择的特征数量趋于增加。特征选择所花费的时间也随着 tol 值接近零而减少。
Total running time of the script: (0 minutes 18.164 seconds)
Related examples